快速幂算法

快速幂

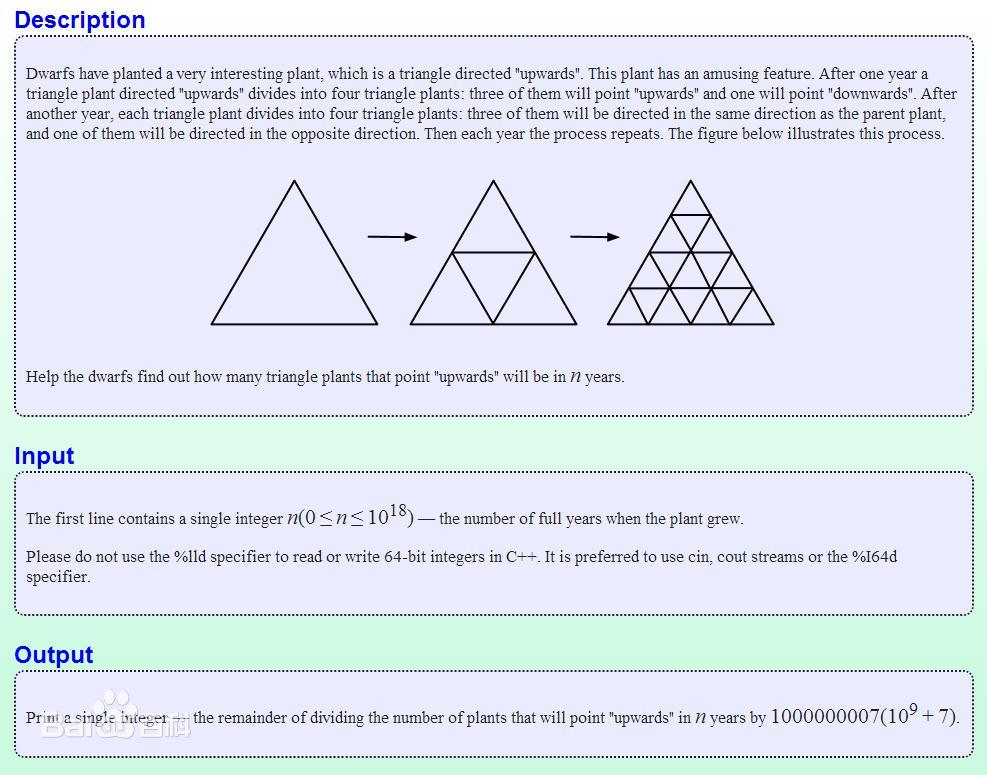
快速幂还是很常用的,例如codeforce上的这道题目:

快速幂就是快速计算底数的n次幂。其时间复杂度为$O(lo{g}_{₂}N)$,与朴素的O(N)相比效率有了极大的提高。

原理

快速幂算法的核心思想就是每一步都把指数分成两半，而相应的底数做平方运算。这样不仅能把非常大的指数给不断变小，所需要执行的循环次数也变小，而最后表示的结果却一直不会变。

举个例子:

计算$3^{10}$,如果按照常规方法去进行计算的话,只能是:
$$3\times 3\times 3\times 3\times 3\times 3\times 3\times 3\times 3\times 3\times 3$$
10个3进行相乘,这就需要去进行9次乘法

但是,如果要将其10写为二进制数字的话,应该为$1010$,也就是$3^{1010}$,即为:

$$3^{1000}\times 3^{000}\times 3^{10}\times 3^0$$

也就是:

$$3^8\times 3^0\times 3^2\times 3^0$$

这样,便可以使得次幂的计算得到改善

代码实现

常规计算次幂的方法

int pow_normal(int d,int m){
    int ans = 1;
    while(m--){
        ans = ans * d;
    }
    return ans;
}

快速幂(一般)

int pow_one(int d, int m){
    int ans = 1;
    while(m){
        if(m%2){ans = ans * d;}
        d = d * d;
        m = m / 2;
    }
    return ans;
}

递归求快速幂

int pow_dg(int d,int m){
    if(m==1) return d;
    int temp = pow_dg(d,m/2);
    return (m%2==0 ? 1 : m)*temp*temp;
}

位运算求快速幂

int pow_wys(int d,int m){
    int ans = 1;
    while(m){
        if(m&1==1){ans = ans * d;}
        d = d * d;
        m>>1;
    }
    return ans;
}