为了解决CPU和主存之间速度不匹配的问题,计算机系统中引入了高速缓存(Chche)的概念。
基本想法:使用速度更快但容量更小、价格更高的SRAM制作一个缓冲存储器,用来存放经常用到的信息;这样一来,CPU就可以直接与Chche交换数据,而不用访问主存了。
这种方案有效的原因:对大量典型的程序分析后,发现在一定时间内,CPU要从主存取指令或数据,只会访问主存局部的地址区域。这是由于指令和数据在内存中是连续存放的,而且有些指令和数据会被多次调用;也就是说,指令和数据在主存中地址分布不是随机的,而是相对的簇聚。这使得CPU执行程序时,访问内存具有相对的局部性;这称为程序访问的局部性原理。
- 时间局部性:如果一个数据现在被访问了,那么以后也很有可能被访问
- 空间局部性:如果一个数据现在被访问了,那么它周围的数据在以后也可能会被访问。
局部性原理是Cache高效工作的理论基础。
1.Cache的基本工作原理
为了方便Cache与主存交换信息,Cache和主存都被划分为了相等的块。Cache块又称Chche行,每块由若干字节组成,块的长度称为块长。由于Cache的容量远小于主存的容量,所以Cache中的块数要远少于主存中的块数,Chche中仅保存主存中最活跃的若干块的副本。
1.Cache工作原理
假设主存按照字节编址,地址用n位二进制码表示,那么主存容量为B;块的大小为16个字节,那么主存中块的个数为:
。如果我们对每个块也做一个编号,其实就对应着地址的前n-4位。
因此,我们将地址分为两部分:主存块号和块内地址。
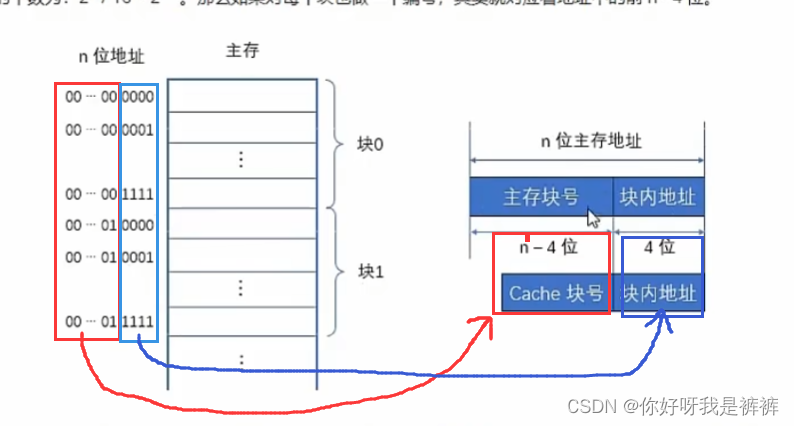
高n-4位表示主存中的“块地址”,低4位表示“块内地址”。
块内地址其实可以看做具体存储字在块内的“偏移量”。
类似,Cache中地址也可以分为这样的两部分。
由于Cache中块长和主存一致,高位是块号,低位是行内地址。
可以按照某种策略预测CPU在未来一段时间内要访问的数据,将其装入Cache。
当CPU要读取主存中的某个字时,可分为两种情况:
- Cache命中:需要的字已经在缓存中,就将其地址转换为缓存地址,直接访问Cache
- Cache未命中:需要的字不再缓存中,仍需访问主存,并将该字所在的块一次性地从主存调入Cache。
如果某个主存块已经调入了Cache,就称它们之间建立了对应关系。
由于Cache容量没有主存大,我们就需要某种替换算法。
将需要调入Cache的信息替换掉之前某个Cache块的信息。
因此,一个缓存块不会永远只对应一个主存块。
==================================================================
总结:CPU与Cache之间的数据交换通常以字为单位;而Cache与主存之间的数据交换则以块为单位。
2.命中率
Cache的效率通常用命中率来衡量。
命中率是指CPU要访问的信息已经在Cache中的比率。
Cache的容量和块长都是影响命中率的重要因素。

3.Cache的基本结构
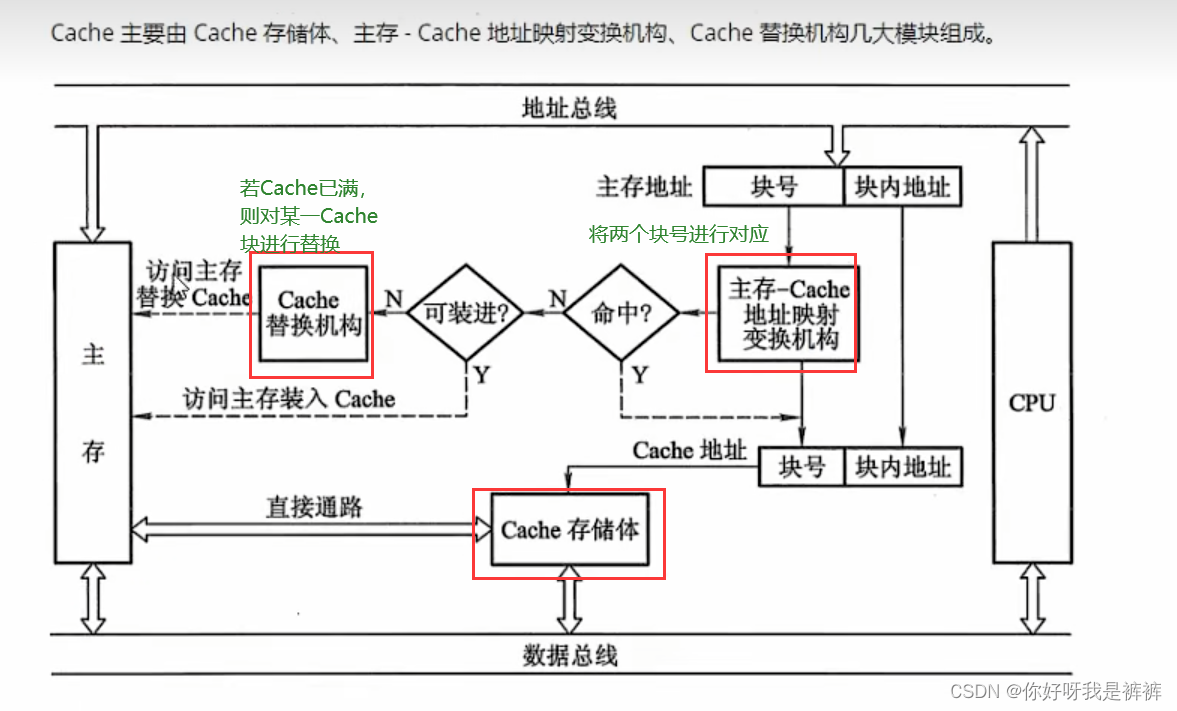
4.Cache的改进
Cache的改进,主要就是由一个缓存改为使用多个缓存
主要有两个方向:增加Cache级数、将统一的Cache改为分立的Cache。
(1)两级缓存
最初在CPU和主存之间只设一个缓存,称为单一缓存。
随着集成电路密度的提高,这个缓存直接与CPU集成在一个芯片中了,所以又称为片内缓存(片载缓存)。
由于片内缓存容量无法做到很大,所以可以考虑在片内缓存和主存之间再加一级缓存,称为片外缓存,也由SRAM组成。
这种有两级缓存的Cache系统被称为“两级缓存”,片内缓存作为第一级(L1),片外缓存作为第二级(L2)。
(2)分立缓存
指令和数据都存放在同一缓存内的Cache被称为统一缓存;
而分立缓存则将其存放在两个缓存中,一个叫指令Cache,另一个叫数据Cache。这两种缓存的选择考虑如下两个因素:
- 主存结构:如果计算机主存中指令、数据是统一存储的,则相应的Cache采用统一缓存;如果主存指令、数据分开存储,则相应的Cache采用分立缓存。
- 机器对指令执行的控制方式:如果采用了超前控制或者流水线控制方式,一般都采用分立缓存。
超前控制,是指在当前指令执行尚未结束时就提前把下一条准备执行的指令取出
流水线控制,就是多条指令同时分阶段执行。(类似于多体低位存储方式)
2.Chche和主存之间的映射
Cache块中的信息是主存中某个块的副本,地址映射是指主存地址空间映射到Cache地址空间,这相当于定义了一个函数:
Cache地址=f(主存地址)
由于Cache块和主存块长一样,而块内地址只是字在当前块内的“偏移量”,所以映射转换之后块内地址是不变的。我们仅仅需要Cache块号和主存块号之间的函数关系。
Cache地址=f(主存地址)
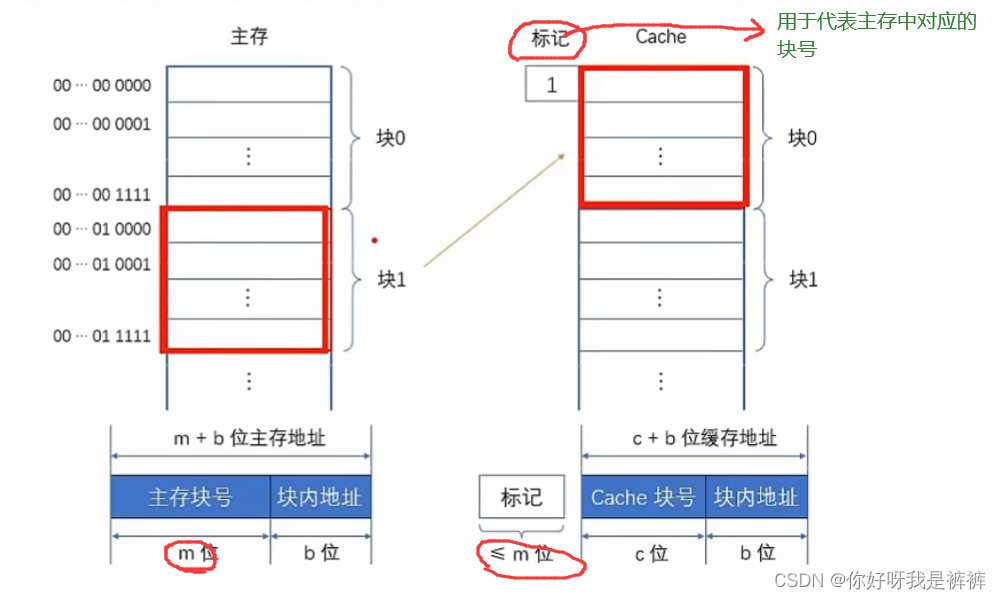
Cache块远少于主存块,所以Cache块不可能永远对应唯一的主存块,需要在Cache中为每一个块加一个标记,指明它是主存中哪一块的副本。这个标记的内容,应该能够唯一确定对应主存块的编号。
另外,为了说明Cache行中的信息是否有效,每个Cache行还需要一个有效位,该位为1时,表示Cache中该映射的主存块数据有效;为0则无效。
地址映射的方式有如下3种:
1.直接映射
直接映射的思路非常简单,就是“挨个对应”,主存中的每一块只能装入Cache中的唯一位置。
由于Cache容量很小,当主存中的块已经“遍历”完所有Cache地址后,下一个主存块的对应位置就又成了Cache中的第一行(第一个块)。
很明显,这跟“顺序存储”的思路是一样的,用主存块数对Cache的总行数取模,就可以得到对应的Cache的行号了:
Cache行号=主存行号 mod Cache总行数
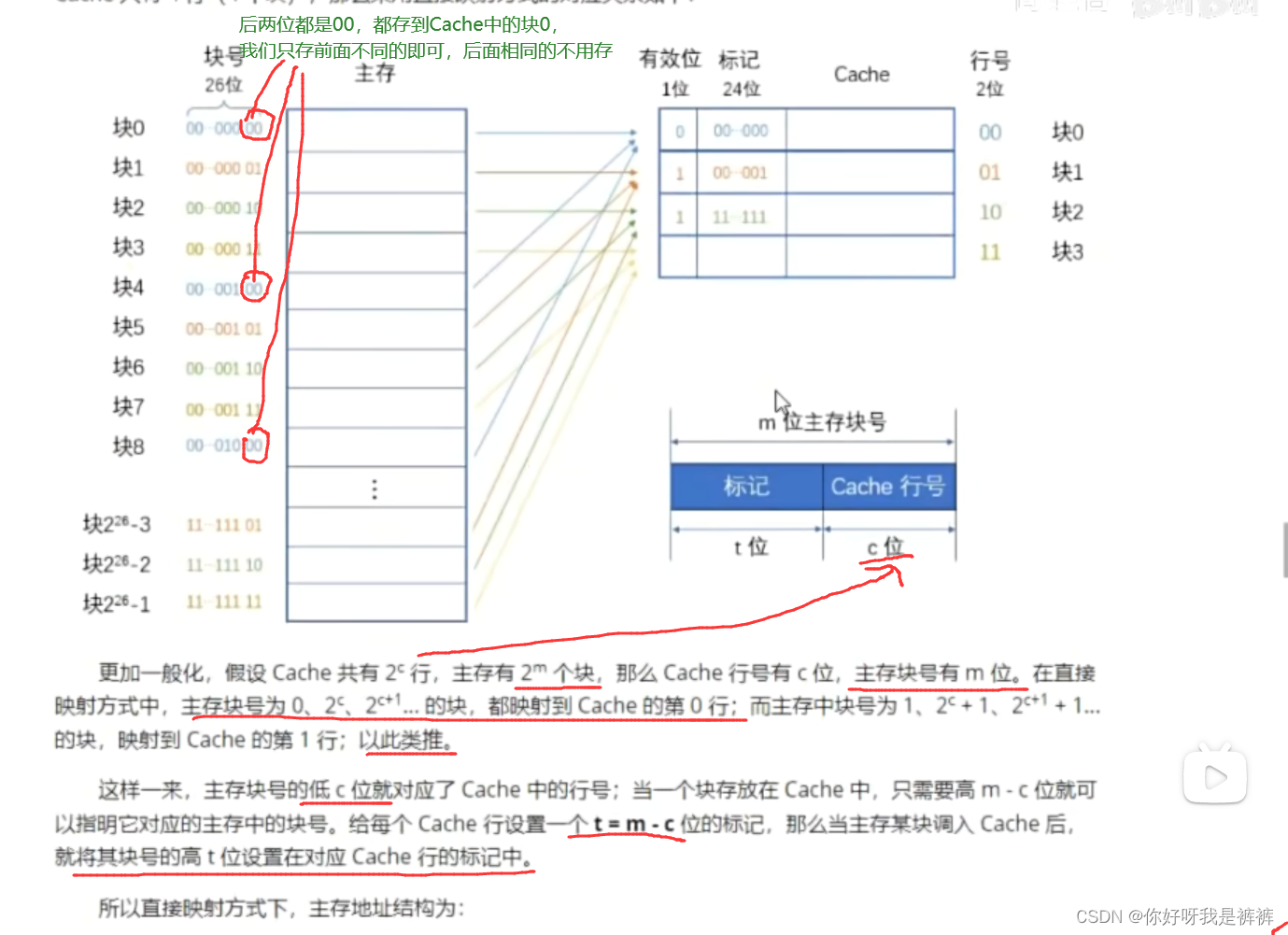
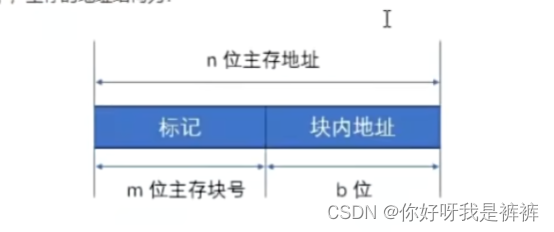
因此,直接映射方式下,主存地址结构为:
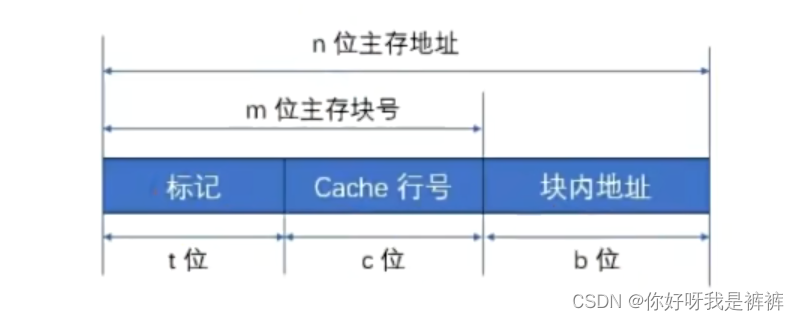
访问内存的过程:
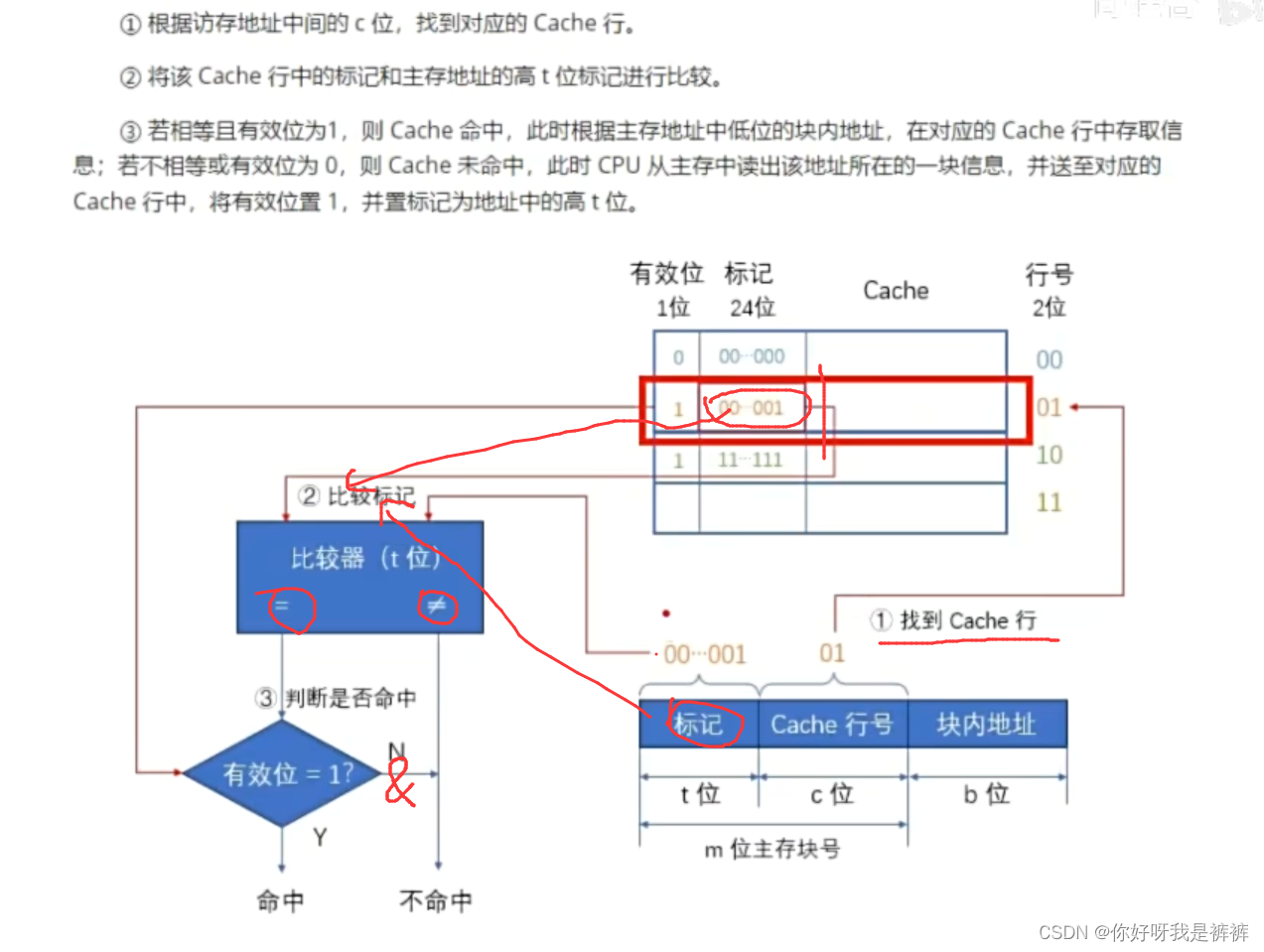
2.全相联映射
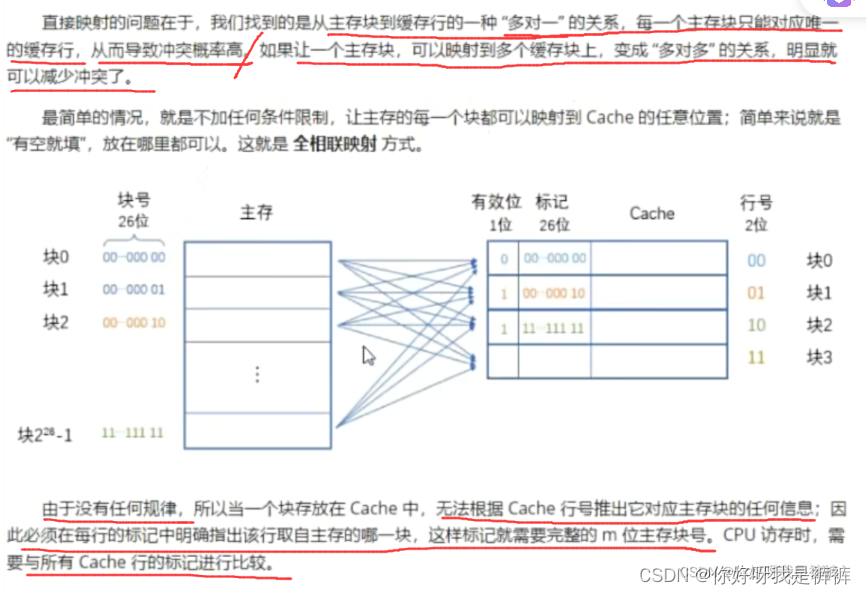
全相联映射方式下,主存的地址结构为:
全相联映射方式的优点是灵活,Cache行的冲突概率低,空间利用率高,命中率也高;缺点是标记的速度较慢(标记变长了),实现成本较高。
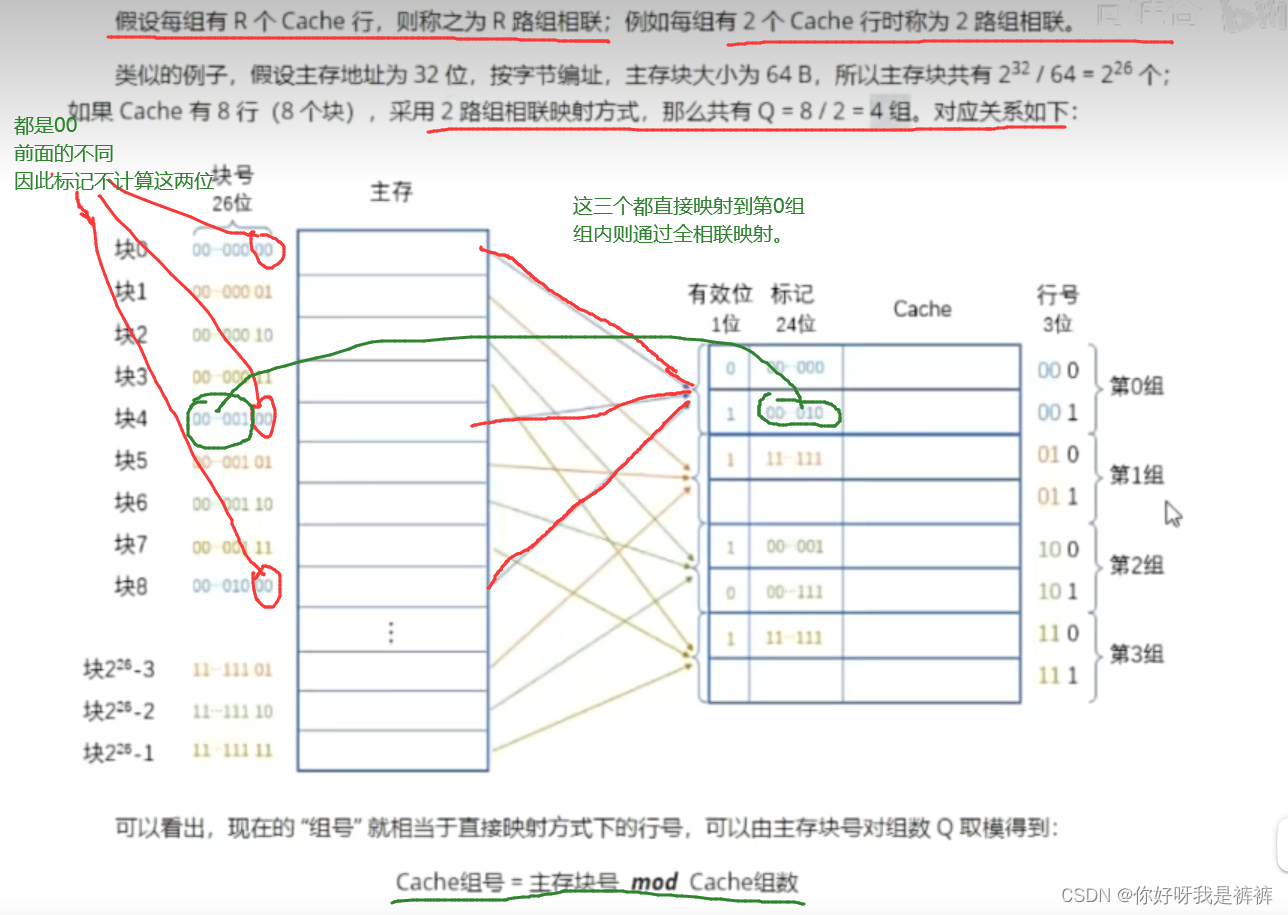
3.组相联映射
把直接映射和全相联映射两种方式结合起来,就是组相联映射方式。
组相联的思路就是将Cache行分为Q个大小相等的组,每个主存块可装入对应组的任意一行;
它所在的组则按照顺序依次排列得到。
也就是组间采用直接映射、而组内采用全相联映射的方式。
当Q等1时,则是全相联映射
当Q等于Cache时,则是直接映射。
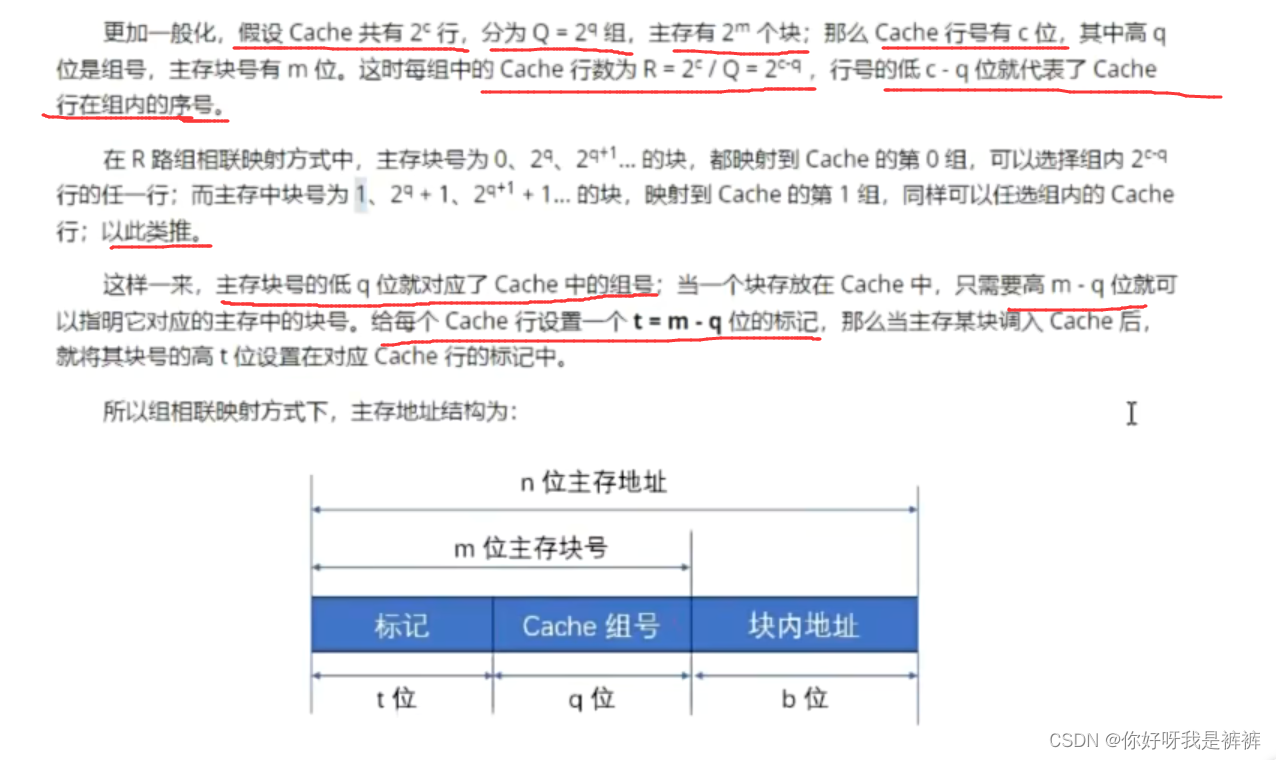 访问过程以及三种映射方式的区别
访问过程以及三种映射方式的区别
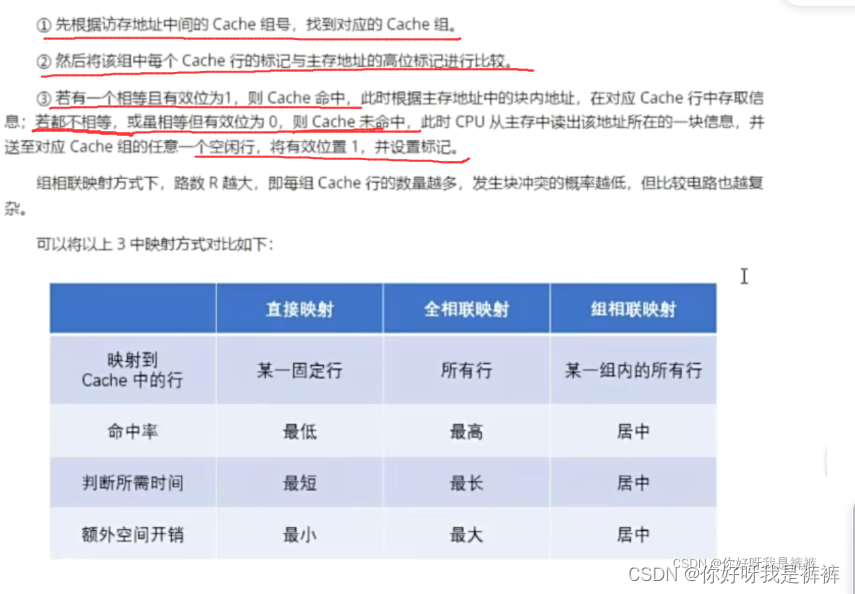
3.Cache中主存块的替换算法

最不经常使用算法一者是可能二者都为0或者同一个不为0的数,从而导致随机替换
二者是不具备时间累计的性质,无法确定上次使用是什么时候。
这里我们最常使用LRU算法:
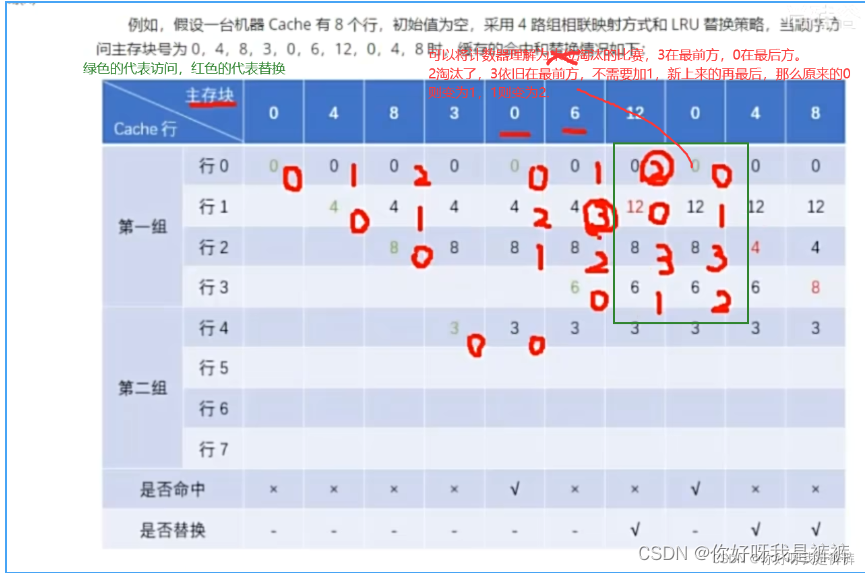

4.Cache写策略
我们的Cache写分为命中和未命中两种情况
(1)Cache写命中
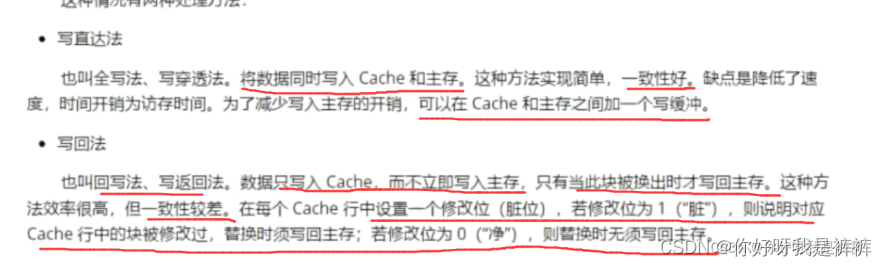
(2)Cache写未命中

Cache行的表示:
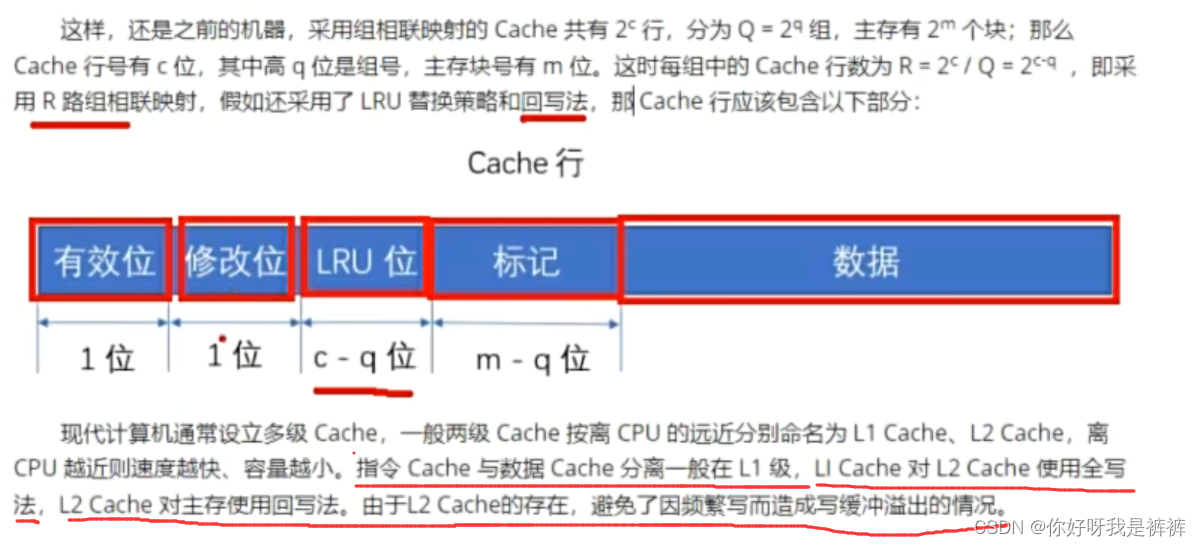





![洛谷 P10584 [蓝桥杯 2024 国 A] 数学题(整除分块+杜教筛)](https://img-blog.csdnimg.cn/direct/674b6510d76b452aac61ec4526244379.png)