二、频域分析
随机信号的时域分析只能提供有限的时域故障特征信息,故障发生时往往会引起信号频率结构的变化,而故障频率可以计算和预知,通过检测频率的幅值变换规律,就可以监控故障的发展过程。
频谱分析的理论基础是傅里叶变换,傅里叶变换包括傅里叶级数和傅里叶积分。
2.1 傅里叶级数
满足Dirichlet条件的周期信号X(t)可以分解为很多谐波分量之和:
其中
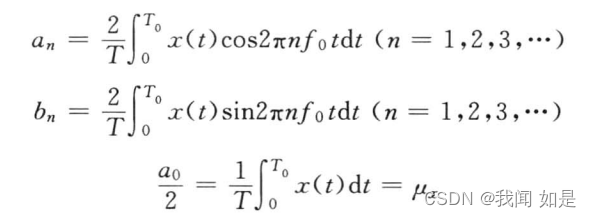
傅里叶级数的概念是任何一个周期函数都可以采用无限个三角函数去拟合和描述。
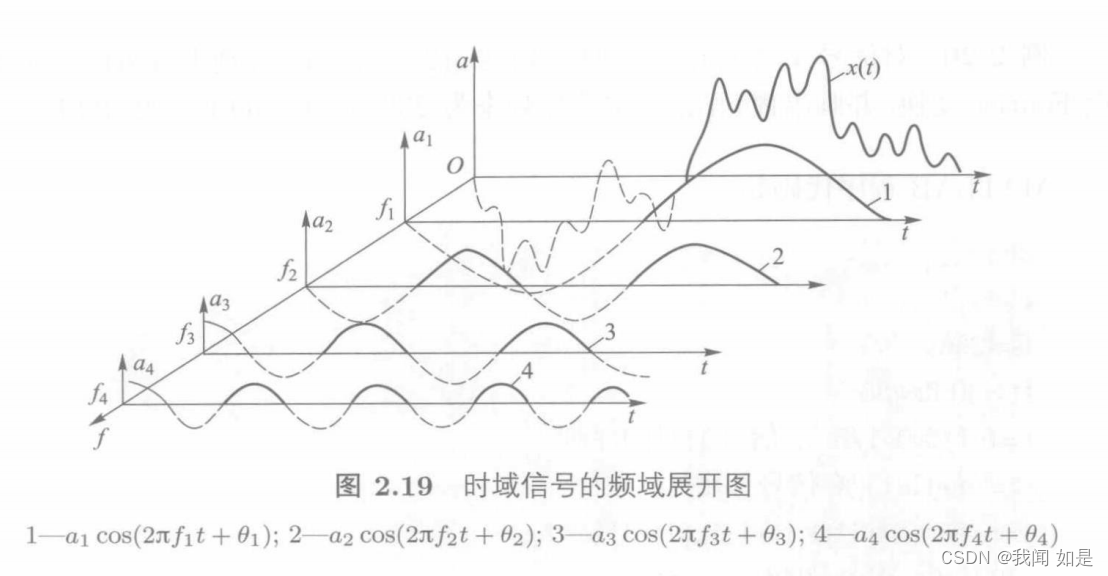
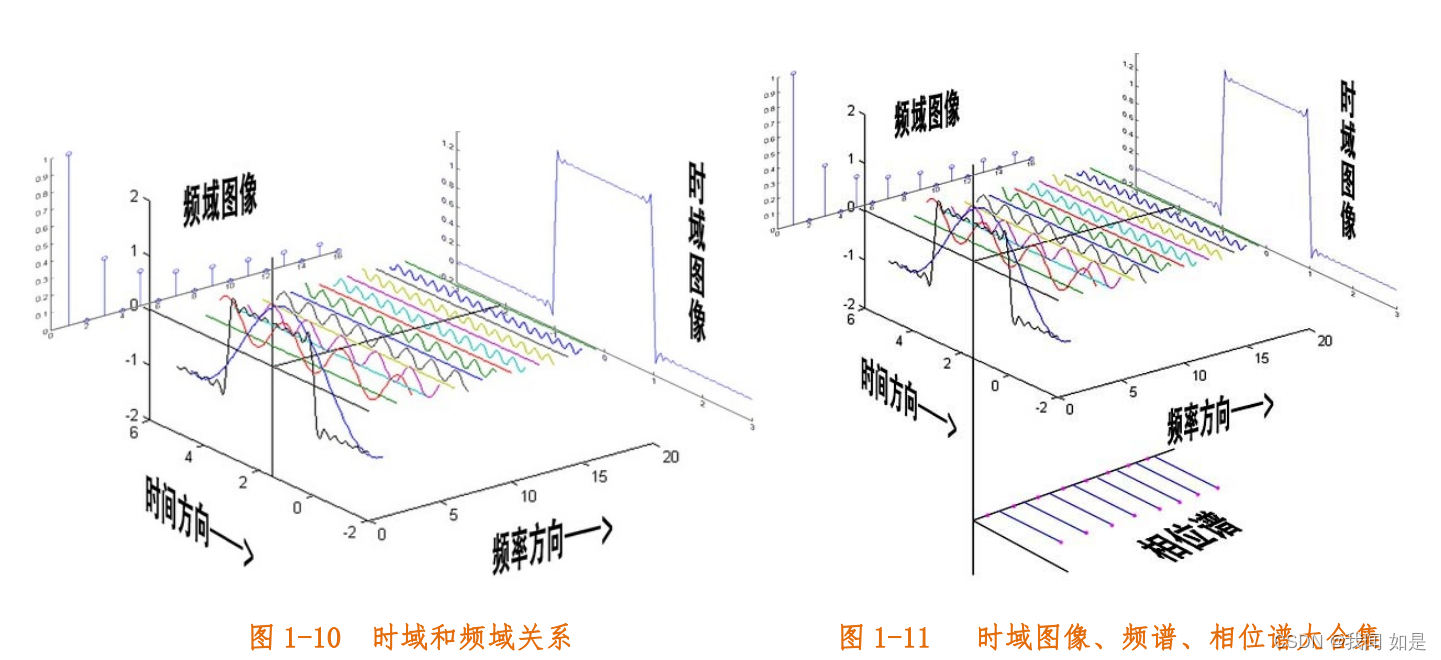
时域分析和频域分析只是从不同侧面反映信号。
2.2 傅里叶变换
傅里叶变换对
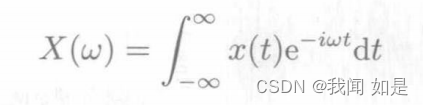
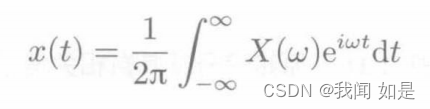
为了计算机上实现信号的频谱分析,需要时域信号是离散的,且是有限长。
离散傅里叶变换公式为:
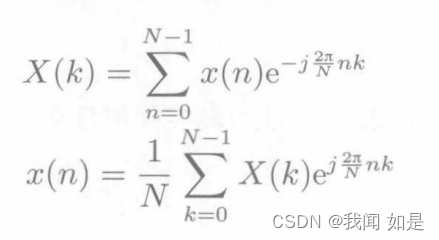
傅里叶分析的不足:
变换之后的信号完全失去了时间信息,无法反映频率随时间的变化。
傅里叶变换命令
y=fft(x)
y=fft(x,n) n表示执行n点fft
若x的长度是2的整数次幂,函数fft运行速度最佳。
傅里叶逆变换命令
y=ifft(x)
y=ifft(x,n)
例3. 对信号分别64点,256点进行fourier变换,并画出幅频图,采样频率256Hz。
clc
clear
close all
fs=256;
f1=30;
f2=80;
t=0:1/fs:1-1/fs;
p=length(t);
y=2*sin(2*pi*f1.*t)+sin(2*pi*f2.*t);
nfft1=64;
nfft2=256;
rfft1=fft(y,nfft1);
ys1=abs(rfft1);
fz1=(1:nfft1/2)*fs/nfft1;
figure(1)
subplot(211)
plot(fz1,ys1(1:nfft1/2)*2/p)
xlabel('频率/Hz')
ylabel('幅值')
title('64点fft')
rfft2=fft(y,nfft2);
ys2=abs(rfft2);
fz2=(1:nfft2/2)*fs/nfft2;
subplot(212)
plot(fz2,ys2(1:nfft2/2)*2/p);
xlabel('频率/Hz')
ylabel('幅值')
title('256点fft')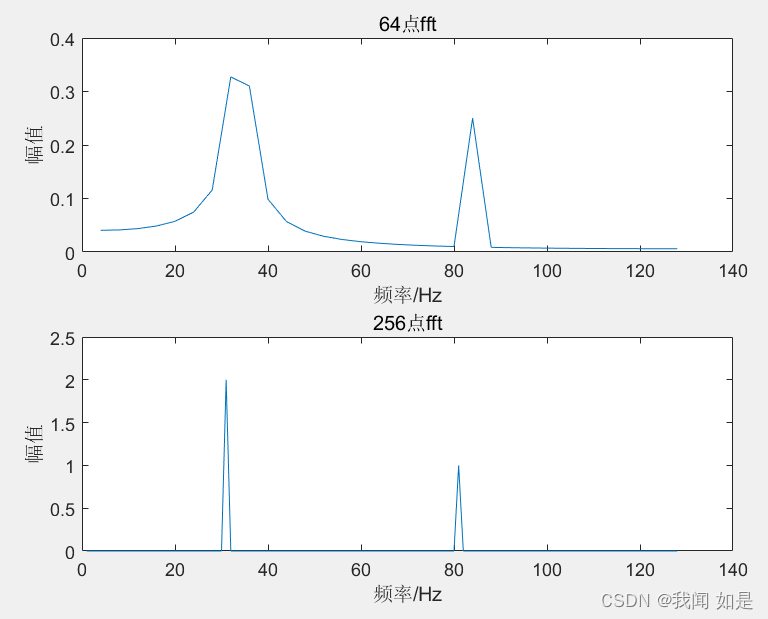
从上图可以看出,采样频率越多,频谱图效果越好。
例4.对例3的信号进行fft逆变换,与原信号对比。
clc
clear
close all
fs=256;
f1=30;
f2=80;
t=0:1/fs:1-1/fs;
p=length(t);
y=2*sin(2*pi*f1.*t)+sin(2*pi*f2.*t);
nfft=256;
rfft=fft(y,nfft);
ys=abs(rfft);
fz=(1:nfft/2)*fs/nfft;
xifft=ifft(rfft);
realx=real(xifft);
ti=[0:length(xifft)-1]/fs;
yfft=fft(xifft,nfft);
myfft=abs(yfft);
p1=length(xifft);
figure(1)
subplot(221)
plot(t,y)
xlabel('时间/s')
ylabel('幅值')
title('原始信号')
subplot(222)
plot(fz,ys(1:nfft/2)*2/p);
xlabel('频率/Hz')
ylabel('幅值')
title('原始信号的fft')
subplot(223)
plot(ti,realx);
xlabel('时间/s')
ylabel('幅值')
title('逆变换后的信号')
subplot(224)
plot(fz,myfft(1:nfft/2)*2/p1);
xlabel('频率/Hz')
ylabel('幅值')
title('逆变换后得到的信号的fft')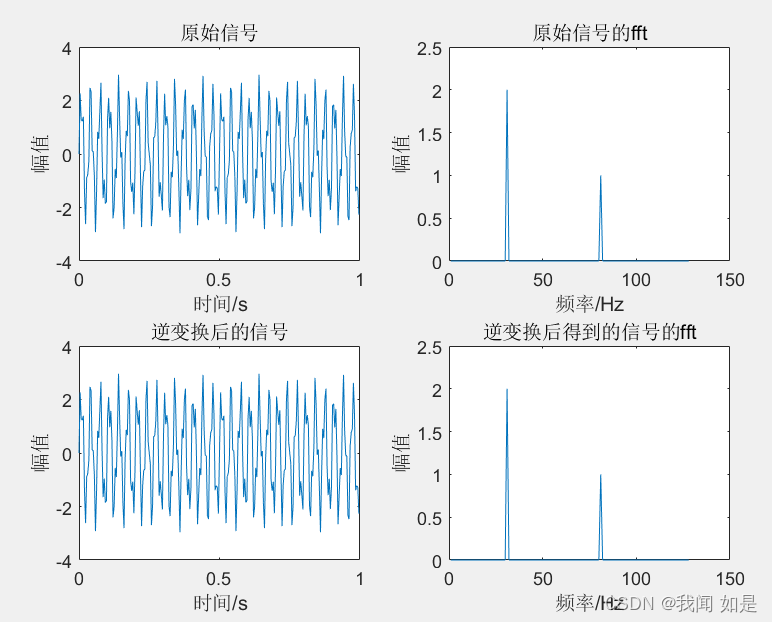
例5 对西储大学的数据进行傅里叶变换
clc,
clear,
close all;
load 130.mat
x = X130_DE_time;
fs = 12000;
N=length(x); %采样频率和数据点数
t = 0:1/fs:(N-1)/fs;
y = fft(x,N);
y1 = abs(y);
ayy = y1/(N/2);
ayy(1) = ayy(1)/2;
f = ((1:N)-1)*fs/N;
subplot(211)
tt=1000:1500;
plot(tt,x(tt),'color',[0/255,0/255,255/255],'LineWidth',0.8);
title('时域分析')
xlabel('时间(t)')
ylabel('m/s^2')
subplot(212)
plot(f(1:(N-1)/2),ayy(1:(N-1)/2),'color',[0/255,0/255,255/255],'LineWidth',0.8);
grid on
%xlim([0 500])
xlabel('频率[f]');
ylabel('Amplitude(m/s^2)')
title('频域分析')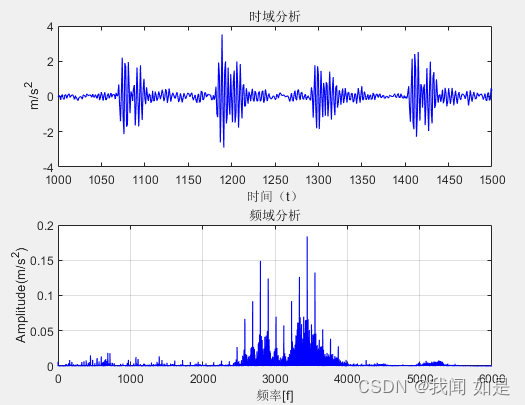
参考资料:
[1] 时献江 《机械故障诊断及典型案例解析》
[2]张玲玲 《基于matlab的机械故障诊断技术案例教程》
[3]傅里叶分析之掐死教程(完整版)更新于2014.06.06 - 知乎 (zhihu.com)