# 本科学习的全都还回去了-_-

一、向量

（1）点乘

向量点积， 𝑎⋅𝑏=𝑐 ，符号为 ⋅ ，要求向量长度相同，是两个向量之间的点乘运算，结果是一个标量。又称：点乘、数量积、标量积、scalar product、projection product等。

a · b = a₁b₁ + a₂b₂ + ... + aᵢbᵢ

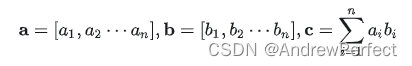
在Python中，可以使用NumPy库来计算向量的点乘：

示例代码

	import numpy as np 

	
	# 定义两个向量 

	a = np.array([1, 2, 3]) 

	b = np.array([4, 5, 6]) 


	# 计算点乘 

	dot_product = np.dot(a, b) 

	print("点乘结果:", dot_product)

 

（2）叉乘

与向量点乘不同，叉乘仅适用于三维向量，向量叉乘的运算结果是一个向量而不是一个标量。两个向量叉乘所得向量与这两个向量垂直，如下图所示。

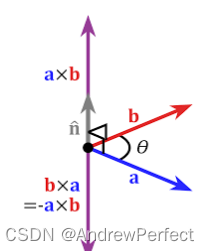
示例代码：

import numpy as np 


# 定义两个三维向量 
a = np.array([1, 2, 3]) 
b = np.array([4, 5, 6]) 


# 计算叉乘（注意：NumPy的cross函数仅适用于三维向量） 
cross_product = np.cross(a, b) 
print("叉乘结果:", cross_product)

 

二、矩阵

（1）点乘

矩阵的点乘（也称为元素乘法或哈达玛乘积）是两个相同大小矩阵之间的一种运算，其结果是一个与这两个矩阵大小相同的新矩阵，其中每个元素都是原矩阵对应位置元素的乘积。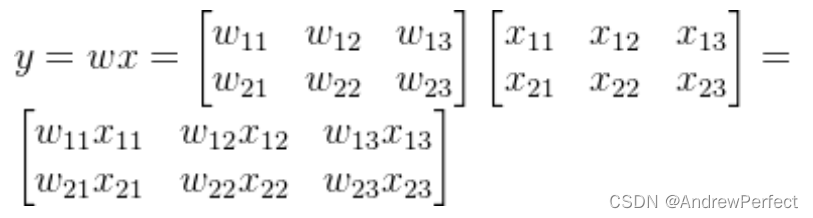

ps: 向量可以看作是一个列矩阵或行矩阵，

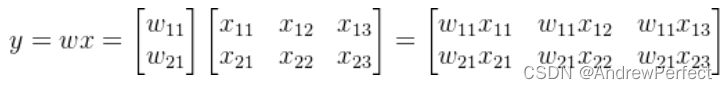
实例代码：

A = np.array([[1],[2]])
B = np.array([[1,2,4],[1,4,5]])
C = np.array([[1,2,3],[4,5,6]])
 
X = A*B
array([[ 1,  2,  4],
       [ 2,  8, 10]])
 
X == np.multiply(A,B)
array([[ True,  True,  True],
       [ True,  True,  True]])
 
Y = B*C
array([[ 1,  4, 12],
       [ 4, 20, 30]])
Y == np.multiply(B,C)
array([[ True,  True,  True],
       [ True,  True,  True]])

（2）叉乘

矩阵乘法是两个矩阵之间的一种运算，其结果是一个新矩阵。对于矩阵A（m×n）和矩阵B（n×p），只有当A的列数等于B的行数时，才能进行乘法运算，结果矩阵C的大小为m×p。

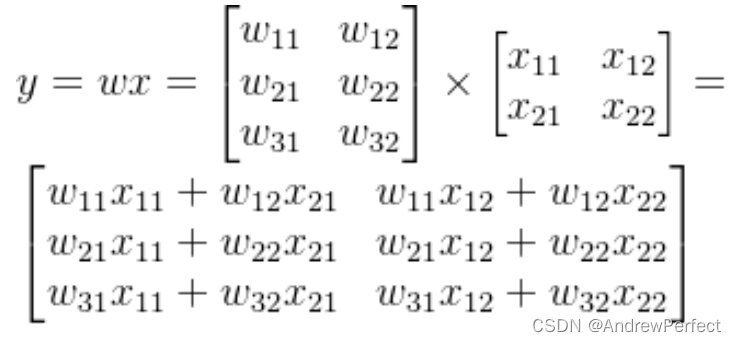
实例代码：

A = np.array([[1,2],[3,4],[1,5]])
B = np.array([[1,2],[2,1]])
 
A@B
array([[ 5,  4],
       [11, 10],
       [11,  7]])
 
A@B  == np.dot(A,B)
array([[ True,  True],
       [ True,  True],
       [ True,  True]])