文章目录
- 前言
- 一、布尔可满足性问题
- 二、每子句至多3个变量的布尔可满足性问题(3-SAT)
- 三、0-1整数规划(0-1 integer programming)
- 四、Set packing(Set packing)
- 五、最小顶点覆盖问题(Vertex cover)
- 六、集合覆盖问题(Set covering)
- 七、Feedback node set
- 八、Feedback arc set
- 九、有向哈密顿循环(Directed Hamiltonian cycle)
- 十、无向哈密顿循环(Undirected Hamiltonian cycle)
- 十一、图着色问题(Chromatic number)
- 十二、分团覆盖问题(Clique cover)
- 十三、精确覆盖问题(Exact cover)
- 十四、Hitting set(Hitting set)
- 十五、Steiner tree(Steiner tree)
- 十六、三维匹配问题(3-dimensional matching)
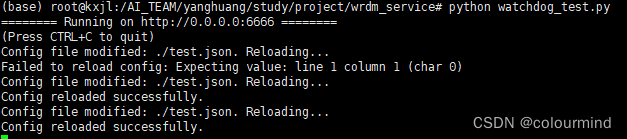
- 在这里插入图片描述
- 十七、背包问题(Knapsack)
- 十八、Job sequencing(Job sequencing)
- 十九、划分问题(Partition)
- 二十、最大割(Max cut)
- 二十一、分团问题(Clique,参考独立集)
前言
P问题:可以在多项式的时间里找到解决它的算法的问题。
NP问题:可以在多项式的时间里验证一个解的问题。
NPC问题:是一个NP问题,并且所有的NP问题都可以约化到它。
NP-Hard问题:满足NPC问题定义的第二条但不一定要满足第一条。
一、布尔可满足性问题
问题描述:
由 N个布尔变元X1,X2,X3…Xn,和M个布尔连接符(如:与、或、非、蕴含、等价…)构成的布尔表达式F,如果存在一组布尔变元和布尔连接符实例,判别F输出为1,则为可满足。
证明过程:
1.证明SAT是NP问题:
对于给定的布尔表达式和一个可能的赋值,可以在多项式时间内验证这个赋值是否使得表达式为真。这个验证过程只需要简单地计算表达式的值即可,因此SAT属于NP类问题。
2.证明SAT问题至少和某个已知的NPC问题一样难:
给定一个3SAT问题,可以将每个子句拆分成一个或多个布尔表达式,每个表达式对应于3SAT中的一个子句。如果可以在多项式时间内找到一个赋值使得原始3SAT问题可满足,则相应的SAT问题也可满足;反之亦然。)
二、每子句至多3个变量的布尔可满足性问题(3-SAT)
问题描述
3SAT问题是一个经典的布尔可满足性问题,也是计算理论中一类NP完全问题的代表。3SAT问题是指给定一个由布尔变量、逻辑符号(如与、或、非)和小括号构成的逻辑公式,其中每个子句由三个布尔变量或者其否定构成,并且整个公式是用与逻辑符号连接的。问题的目标是确定是否存在一组布尔变量的赋值,使得整个公式为真。
证明过程:
1.证明3SAT是NP问题
要证明3SAT属于NP类,我们需要证明给定一个3SAT公式和一个赋值,我们可以在多项式时间内验证该赋值是否满足公式。具体步骤如下:
给定一个布尔公式,该公式由多个子句组成,每个子句最多包含3个字面(变量或它们的否定)。
给定一个赋值,我们可以逐个检查每个子句,看是否至少有一个字面为真。
如果所有子句都满足,则该赋值是可满足的;否则,不是可满足的。
由于每个子句最多包含3个字面,验证每个子句的时间是常数级别,因此整个验证过程的时间复杂度是多项式级别的。
因此,3SAT属于NP类。
2.证明将3SAT问题至少和某个已知的NPC问题一样难
要证明3SAT是NP完全问题,我们需要证明任何一个NP问题都可以在多项式时间内归约到3SAT问题。我们从SAT问题出发,将其多项式时间归约到3SAT问题。
将一般的SAT公式转换为3SAT公式,将每个子句分解为不超过3个符号的子句:
如果子句已经包含1个或2个符号,则我们可以通过添加重复的符号来扩展成3个符号。例如,子句(x1)可以转换为(x1 ∨ x1 ∨ x1),子句(x1 ∨ x2)可以转换为(x1 ∨ x2 ∨ x2)。
将超过3个符号的子句拆分为多个3字面子句:
对于超过3个符号的子句,我们可以引入新的辅助变量,将其拆分成多个3符号子句。例如,对于子句(x1 ∨ x2 ∨ x3 ∨ x4),我们可以引入一个新的辅助变量y1,将其转换为:
(x1 ∨ x2 ∨ y1) ∧ (¬y1 ∨ x3 ∨ x4)
这种方法可以保证每个子句都被转换为3个符号子句,并且整个转换过程在多项式时间内完成。因此,我们可以将任意的SAT问题多项式时间归约为3SAT问题。
三、0-1整数规划(0-1 integer programming)
问题描述
01整数规划问题是一类特殊的整数规划问题,其中所有决策变量的取值只能为0或1。这类问题在组合优化、计算机科学、运筹学等领域中非常常见,例如在网络流、资源分配、任务调度等实际问题中都有应用。给定一个目标函数和一组约束条件,我们需要找到一组满足所有约束条件的01变量值,使得目标函数达到最优(最大或最小)。
证明过程:
1.证明0-1整数规划问题属于NP:

2.证明0-1整数规划问题至少和某个已知的NPC问题一样难:

四、Set packing(Set packing)
问题描述
Set Packing 问题是一个组合优化问题,给定一个集合的集合(通常称为“超集”或“宇宙”U),以及一系列子集 S_1, S_2, …, S_n,其中每个 S_i 都是 U 的子集。Set Packing 问题的目标是找到这些子集的一个子集(称为“packing”),使得 packing 中的任何两个子集都不相交(即它们的交集为空集)。
证明过程:
1.Set Packing 是 NP 问题
给定一个子集集合 S_1, S_2, …, S_n 和一个可能的 packing P(即 P 是 S_1, S_2, …, S_n 的一个子集),验证 P 是否是一个有效的 packing 可以通过检查 P 中任意两个子集 S_i 和 S_j(其中 i ≠ j)的交集是否为空集来完成。这可以在多项式时间内完成,因为子集的数量是有限的,且检查两个集合的交集是否为空集是一个常数时间操作。
2.Set Packing 至少和 3SAT 问题一样难
我们将使用 3SAT 问题的实例来构造一个 Set Packing 问题的实例。
假设我们有一个 3SAT 问题的实例,其中包含 m 个子句和 n 个变量 x_1, x_2, …, x_n。
对于每个变量 x_i,我们创建两个集合 X_i 和 Xbar_i,分别表示 x_i 为真和 x_i 为假的情况。具体来说,如果 x_i 在某个子句中以正文字的形式出现,则将该子句对应的元素添加到 X_i 中;如果 x_i 在某个子句中以负文字的形式出现,则将该子句对应的元素添加到 Xbar_i 中。
对于每个子句 C_j(假设它包含文字 l_1 ∨ l_2 ∨ l_3),我们创建一个集合 C_j,它包含三个元素,分别对应于这三个文字。
宇宙 U 是所有 X_i、Xbar_i 和 C_j 的并集。
Set Packing 问题的目标是找到一个 packing,即找到一个子集集合,使得这个集合中的任何两个子集都不相交。由于每个 C_j 都与三个 X_i 或 Xbar_i 集合相交(对应于子句 C_j 中的三个文字),因此一个有效的 packing 必须包含恰好一个与每个 C_j 相交的 X_i 或 Xbar_i 集合。这对应于为 3SAT 问题中的每个子句选择一个使其为真的文字。
因此,如果 3SAT 问题有一个解(即一个满足所有子句的变量赋值),则 Set Packing 问题也有一个解(即一个有效的 packing)。反之亦然。
归约过程可以在多项式时间内完成,因为我们只需要遍历 3SAT 问题中的每个子句和变量来构造 Set Packing 问题的实例。
五、最小顶点覆盖问题(Vertex cover)
问题描述
最小顶点覆盖问题(Minimum Vertex Cover Problem)是一个图论中的经典问题,其定义如下:给定一个无向图G = (V, E),其中V是顶点集,E是边集。一个顶点覆盖是一个顶点子集C ⊆ V,使得图中的每一条边都至少有一个端点在C中。最小顶点覆盖问题则是寻找一个顶点数最小的顶点覆盖。
证明过程
1.最小顶点覆盖问题是NP问题:
给定一个无向图G = (V, E)和一个顶点子集C ⊆ V,验证C是否是G的一个顶点覆盖是容易的。我们只需要遍历G中的所有边,对于每条边(u, v),检查u或v(或两者)是否在C中。如果对于所有边都满足这个条件,那么C就是一个顶点覆盖。这个过程可以在多项式时间内完成,因为边和顶点的数量是有限的。
2.最小顶点覆盖问题少和某个已知的NPC问题一样难
假设我们有一个集合覆盖问题的实例,它由一个宇宙集合U和一系列子集S_1, S_2, …, S_m组成,目标是找到一个最小的子集集合,使得这些子集的并集等于U。
我们可以将集合覆盖问题归约到最小顶点覆盖问题。对于集合覆盖问题中的每个元素u ∈ U,我们创建一个顶点v_u。对于集合覆盖问题中的每个子集S_i,我们创建一个顶点w_i,并在w_i和S_i中所有元素的对应顶点之间添加边。这样,我们就得到了一个无向图G。
集合覆盖问题的一个解对应于图G的一个顶点覆盖:对于集合覆盖问题中的每个选定的子集S_i,我们选择对应的顶点w_i;对于U中剩余的元素(即未被任何选定子集覆盖的元素),我们选择它们对应的顶点。这个顶点集合就是一个顶点覆盖,因为图中的每条边都至少有一个端点在这个集合中(要么是一个w_i顶点,要么是一个v_u顶点,其中u是某个S_i中的元素)。
反过来,图G的一个最小顶点覆盖也对应于集合覆盖问题的一个解:对于每个选定的w_i顶点,我们选择对应的子集S_i;对于每个选定的v_u顶点(其中u不在任何S_i中),我们可以忽略它,因为它不影响集合的覆盖性。
因此,如果集合覆盖问题有一个解(即一个覆盖U的子集集合),则最小顶点覆盖问题也有一个解(即一个顶点覆盖)。反之亦然。由于集合覆盖问题是NP完全的,所以最小顶点覆盖问题也是NP完全的。
六、集合覆盖问题(Set covering)
问题描述
集合覆盖问题(Set Covering Problem)是一个组合优化问题,其定义如下:给定一个宇宙集合U和一组集合S = {S_1, S_2, …, S_m},其中每个S_i都是U的子集。集合覆盖问题的目标是找出S的一个最小子集(称为覆盖),使得这个子集中所有集合的并集等于U。
证明过程
1.证明集合覆盖问题是NP问题
验证解的有效性:给定一个集合子集C ⊆ S,验证C是否是U的一个覆盖是容易的。我们只需要遍历C中的每个集合,并将它们合并,检查合并后的集合是否包含U中的所有元素。这个过程的时间复杂度是多项式的,因为集合的数量和每个集合中元素的数量都是有限的。
结论:因此,集合覆盖问题满足NP问题的定义,即解的有效性可以在多项式时间内验证。
2.证明集合覆盖问题至少和某个已知的NPC问题一样难
选择已知的NPC问题:我们选择顶点覆盖问题(Vertex Cover Problem)
归约过程:
给定一个顶点覆盖问题的实例,即一个无向图G = (V, E)和一个整数k,我们要构造一个集合覆盖问题的实例。
对于图G中的每个顶点v_i ∈ V,我们创建一个集合S_i,该集合包含与v_i相邻的所有边的标识符。
宇宙集合U由G中所有边的标识符组成。
现在,我们要求解集合覆盖问题,即找出S的一个最小子集C,使得U中所有元素都被C中的集合覆盖。
注意到,C中的每个集合S_i对应于图G中的一个顶点v_i。因此,如果C是一个大小为k的集合覆盖,那么对应的顶点集合{v_i | S_i ∈ C}就是一个大小为k的顶点覆盖。
归约的正确性:
如果顶点覆盖问题有一个解(即一个大小为k的顶点覆盖),则集合覆盖问题也有一个解(即一个大小为k的集合覆盖)。因为对于每个被选择的顶点v_i,其对应的集合S_i包含了与v_i相邻的所有边的标识符,从而覆盖了这些边。
反之,如果集合覆盖问题有一个解(即一个大小为k的集合覆盖),则顶点覆盖问题也有一个解(即一个大小为k的顶点覆盖)。因为每个被选择的集合S_i都对应于一个顶点v_i,且S_i中的元素都是与v_i相邻的边的标识符。
归约的多项式性:归约过程可以在多项式时间内完成,因为我们只需要遍历图G的所有顶点和边来构造集合覆盖问题的实例。
七、Feedback node set
问题描述
Feedback Node Set(FNS)问题是一个图论问题,给定一个无向图G = (V, E),一个反馈节点集F是V的一个子集,使得从V - F(即F的补集)中删除所有顶点后,剩余的图(如果有的话)是无环的(即是一个森林)。Feedback Node Set问题的目标是找到最小的反馈节点集,即包含最少顶点的集合F,使得G - F是无环的。
证明过程
1.证明问题是NP问题
验证解的有效性:给定一个顶点集F作为候选的反馈节点集,验证其是否有效(即是否使得G - F成为无环图)可以通过深度优先搜索(DFS)或广度优先搜索(BFS)遍历G - F中的所有顶点来完成。如果在遍历过程中没有检测到任何环,那么F就是一个有效的反馈节点集。这个验证过程的时间复杂度是多项式的,因为图的顶点数和边数都是有限的。
2.证明问题至少和某个已知的NPC问题一样难
我们选择3-SAT问题作为已知的NPC问题来进行归约。3-SAT问题是一个逻
归约过程:
构造图的顶点集V:对于3-SAT问题中的每个变量x_i,我们创建两个顶点v_i和v_i’,分别代表x_i为真和x_i为假。此外,对于3-SAT问题中的每个子句C_j,我们创建一个顶点c_j。
构造图的边集E:
对于每个子句C_j中的每个文字(例如x_i或¬x_i),如果文字是正面的(即x_i),则添加边(c_j, v_i);如果文字是负面的(即¬x_i),则添加边(c_j, v_i’)。
对于每个变量x_i,添加边(v_i, v_i’)以表示x_i不能同时为真和假。
构造Feedback Node Set问题的实例:现在我们已经构造了一个图G = (V, E)。Feedback Node Set问题的目标是找到最小的顶点集F,使得G - F是无环的。
如果3-SAT问题有一个解(即一个变量的赋值使得公式为真),那么在这个赋值下,对于每个子句C_j,至少有一个文字为真。因此,在对应的图中,我们可以选择那些代表真文字的顶点(即v_i或v_i’),以及所有子句顶点c_j,作为反馈节点集F。由于每个子句至少有一个真文字,所以G - F中不会有环(因为每个子句顶点c_j都与至少一个真文字顶点相连,而这些真文字顶点在F中)。
反之,如果Feedback Node Set问题有一个解(即一个最小的反馈节点集F),那么我们可以根据F中的顶点来为每个变量x_i分配一个值(如果v_i ∈ F,则x_i为假;如果v_i’ ∈ F,则x_i为真)。由于G - F是无环的,因此每个子句顶点c_j都至少与F中的一个顶点相连,这意味着在3-SAT问题中,每个子句都至少有一个文字为真。
八、Feedback arc set

九、有向哈密顿循环(Directed Hamiltonian cycle)
问题描述
有向哈密顿循环(Directed Hamiltonian cycle)问题是一个在有向图上的判定问题。给定一个有向图G = (V, E),其中V是顶点集,E是弧集,有向哈密顿循环问题是判断图中是否存在一个循环,它恰好经过每个顶点一次且仅一次。
证明过程
1.证明问题是NP问题
验证解的有效性:给定一个有向图G = (V, E)和一个循环C作为候选的有向哈密顿循环,验证其是否有效是容易的。我们可以遍历C中的顶点,检查是否所有顶点V中的元素都恰好出现一次,并且C中的每条弧都在E中。这个验证过程的时间复杂度是O(|V| + |E|),因为我们需要遍历C中的所有顶点和弧。
2.证明问题至少和某个已知的NPC问题一样难
选择已知的NPC问题:我们选择旅行商问题(Traveling Salesman Problem, TSP)作为已知的NPC问题进行归约。TSP是一个经典的NPC问题,它要求在给定的城市集合中找到一条访问每个城市恰好一次并返回起点的最短路径。
归约过程:
给定一个TSP问题的实例,我们可以构造一个有向图G = (V, E)的实例,其中V是城市集合,E是城市之间的所有可能路径(有向边)。对于TSP问题中的每个城市对(u, v)和它们之间的距离d(u, v),我们在G中添加一条从u到v的有向边,并赋予其权重d(u, v)(虽然在这个归约中我们不需要边的权重,但为了保持一致性,我们仍然可以这样做)。
如果TSP问题有一个解(即存在一条访问每个城市恰好一次并返回起点的路径),那么这条路径在G中就是一个有向哈密顿循环,因为它恰好经过每个顶点一次且仅一次。
反之,如果在G中存在一个有向哈密顿循环,那么这个循环就对应TSP问题的一个解,因为它表示了一条访问每个城市恰好一次并返回起点的路径(由于G是根据TSP问题的城市集合构造的,所以循环中的每个顶点都对应一个城市)。
十、无向哈密顿循环(Undirected Hamiltonian cycle)
问题描述
无向哈密顿循环:在无向图G=(V, E)中,若存在一条路径,它经过且仅经过图中的每个顶点一次,并且最终回到起始顶点,形成一个闭环,则称该路径为无向哈密顿循环(或哈密顿回路)。
证明过程
1. 证明无向哈密顿循环是NP问题
验证解的可行性:给定一个无向图G和一个潜在的哈密顿循环,我们可以在多项式时间内验证这个循环是否真正是无向哈密顿循环。这只需要检查该循环是否确实经过且仅经过图中的每个顶点一次,并形成一个闭环。这个过程的时间复杂度与图中的顶点数成正比,因此是多项式时间的。
验证解的最优性:在无向哈密顿循环问题中,我们并不关心“最优性”,因为问题本身就是询问是否存在这样一个循环。所以,一旦我们验证了某个循环是哈密顿循环,它就已经是最优的(即满足问题的要求)。
2.证明问题至少和某个已知的NPC问题一样难
要证明无向哈密顿循环是NP难的,我们需要展示一个已知的NPC问题可以归约到无向哈密顿循环问题。虽然直接归约可能需要一些复杂的构造,但我们可以基于以下观察进行推理:
哈密顿循环问题与旅行商问题(TSP)的相似性:旅行商问题是一个著名的NPC问题,它要求在一个图中找到一条访问所有顶点并返回起始顶点的最短路径。尽管旅行商问题关心的是路径的长度,而无向哈密顿循环问题不关心路径的长度,但两者在结构上非常相似——都要求访问所有顶点一次且仅一次。
归约的可能性:基于这种相似性,我们可以合理地推测,通过某种方式(可能是添加额外的边或顶点,或者调整边的权重),可以将旅行商问题归约到无向哈密顿循环问题。如果这样的归约存在,那么因为旅行商问题是NPC的,无向哈密顿循环问题也必然是NPC的。
十一、图着色问题(Chromatic number)

十二、分团覆盖问题(Clique cover)
问题描述:
分团覆盖问题是一个组合优化问题,它要求在给定的集合系统(由多个集合组成,每个集合是元素的子集)中找出最小的集合子集,使得这些子集的并集包含所有元素。
证明过程
1. 证明问题是NP问题:
验证解(certificate):对于分团覆盖问题的一个候选解(即一组集合),我们可以很容易地验证这组集合的并集是否包含所有元素。这个验证过程可以在多项式时间内完成,因为我们需要遍历所有元素和集合。
多项式时间算法:虽然找到最小覆盖集不是多项式时间的,但验证一个解是否是覆盖集(即它是否覆盖所有元素)是多项式时间的。
因此,分团覆盖问题满足NP问题的定义:存在一个多项式时间的验证算法。
2. 证明问题至少和某个已知的NPC问题一样难:
我们可以使用归约技术来证明分团覆盖问题至少是NP难的。一个常用的归约是将顶点覆盖问题归约到分团覆盖问题。
顶点覆盖问题(Vertex Cover Problem)是一个已知的NPC问题,它要求在一个图中找出最小的顶点子集,使得这些顶点与图中的所有边都至少有一个端点相连。
给定一个顶点覆盖问题的实例(图G和顶点数k),我们可以构造一个分团覆盖问题的实例:将图中的每个顶点视为一个集合,每个集合包含与该顶点相连的所有边的标签(或索引)。然后,目标是在这些集合中找到一个最小的子集,其并集包含所有边的标签。
如果存在一个大小为k的顶点覆盖集,则存在一个大小为k的分团覆盖集(因为每个选中的顶点都对应一个覆盖所有相邻边的集合)。反之亦然。
因此,由于顶点覆盖问题是NPC的,我们可以得出分团覆盖问题也是NPC的。
十三、精确覆盖问题(Exact cover)
问题描述:
精确覆盖问题是一个组合问题,它要求在给定的集合系统中找出一些集合,使得这些集合的并集恰好包含所有元素,且每个元素只在一个集合中出现。
证明过程:
1. 证明问题是NP问题:
验证解:对于精确覆盖问题的一个候选解(即一组集合),我们可以很容易地验证这组集合的并集是否恰好包含所有元素,并且每个元素只在一个集合中出现。这个验证过程可以在多项式时间内完成。
多项式时间算法:虽然找到精确覆盖集不是多项式时间的,但验证一个解是否是精确覆盖集是多项式时间的。
因此,精确覆盖问题满足NP问题的定义。
2. 证明问题至少和某个已知的NPC问题一样难:
我们可以使用归约技术将3-SAT问题归约到精确覆盖问题。
3-SAT问题是已知的NPC问题,它要求确定一个布尔公式(其中每个子句恰好包含3个文字)是否可满足。
给定一个3-SAT问题的实例(一个布尔公式),我们可以构造一个精确覆盖问题的实例:对于每个子句,我们创建一个集合,该集合包含代表该子句中文字(或它们的否定)的元素。然后,目标是在这些集合中找到一个子集,其并集恰好包含所有元素(即每个子句恰好被一个集合覆盖)。
如果存在一个满足的布尔赋值,则存在一个精确覆盖集(因为每个满足的子句都会有一个对应的集合)。反之亦然。
因此,由于3-SAT问题是NPC的,我们可以得出精确覆盖问题也是NPC的。
十四、Hitting set(Hitting set)
问题描述:
Hitting Set 问题是指给定一组集合 {S1, S2, …, Sn} 和一个预算 b,我们需要找到一个集合 H,使得 H 与所有 Si(1 ≤ i ≤ n)都有非空交集,并且 H 的大小不超过预算 b。
证明过程
1. 证明问题是NP问题:
验证解:给定一个候选解 H,验证 H 是否满足条件(即 H 与所有 Si 都有非空交集且 |H| ≤ b)可以在多项式时间内完成。具体地,对于每个 Si,我们检查 H 和 Si 的交集是否为空集,同时检查 H 的大小是否不超过 b。这两个操作都可以在 O(n * |H|) 的时间内完成,其中 n 是集合的数量,|H| 是 H 的大小。
多项式时间算法:虽然找到最优解(即最小的 H)可能不是多项式时间的,但验证一个给定的解是否是 Hitting Set 的解是多项式时间的。
2. 证明问题至少和某个已知的NPC问题一样难:
归约到 Vertex Cover 问题:Vertex Cover 问题是一个已知的 NPC 问题。给定一个图 G 和一个整数 k,Vertex Cover 问题要求找到 G 的一个顶点集合 V’,使得 V’ 中的顶点能够覆盖 G 的所有边,且 |V’| ≤ k。我们可以通过以下方式将 Vertex Cover 问题归约到 Hitting Set 问题:
对于 G 中的每个顶点 v,我们创建一个集合 Sv,该集合包含所有与 v 相邻的边的标识(例如,边的索引或标签)。
这样,我们就得到了一组集合 {S1, S2, …, Sn},其中 n 是 G 的顶点数。
接下来,我们将 k 作为预算 b。
如果存在一个大小为 k 的 Vertex Cover,则它对应的集合(即每个覆盖顶点的 Sv)将构成一个 Hitting Set,因为每个边至少有一个端点在 Vertex Cover 中,所以每个边的标识至少在一个 Sv 中,且总的 Sv 集合大小不超过 k(即 b)。
反之亦然,如果一个 Hitting Set 的大小不超过 b(即 k),则它对应的顶点集合将是一个 Vertex Cover,因为它能够覆盖所有边。
十五、Steiner tree(Steiner tree)

十六、三维匹配问题(3-dimensional matching)
十七、背包问题(Knapsack)
问题描述:
背包问题(Knapsack Problem)是一个经典的组合优化问题。给定一组物品,每种物品都有自己的重量和价值。在限定的总重量内,如何选择物品放入背包,使得背包内物品的总价值最大。
证明过程:
1. 证明背包问题是NP问题
输入:一个物品列表(每个物品有重量和价值),一个背包的总容量,以及一个物品的选择方案(即哪些物品被放入背包)。
步骤:
计算被选物品的总重量。
如果总重量超过背包的总容量,则输出“否”(该方案不是解)。
由于验证过程可以在多项式时间内完成(遍历物品列表的次数是线性的),因此背包问题是NP问题。
2. 证明背包问题至少和某个已知的NPC问题一样难
为了证明背包问题是NPC问题,我们可以使用归约法,将已知的NPC问题归约到背包问题。这里我们选择子集和问题(Subset Sum Problem)作为已知的NPC问题。
输入:子集和问题的一个实例,包括一组正整数A = {a_1, a_2, …, a_n}和一个目标整数T。
构造:
对于子集和问题中的每个整数a_i,创建一个物品,其重量为a_i,价值也为a_i。
构造背包问题的一个实例,其中背包的总容量为T,物品列表就是上面创建的物品。
输出:如果背包问题有一个解(即存在一个物品子集,其总重量等于背包的总容量T),那么这个子集的和也一定等于T,因此它对应于子集和问题的一个解。反之,如果子集和问题有一个解,那么它也对应于背包问题的一个解(即选择那些和为目标整数的物品)。
十八、Job sequencing(Job sequencing)
问题描述:
Job sequencing问题(也称为Job Scheduling Problem)是一个优化问题,其中有一系列需要完成的作业,每个作业都有一个截止时间和一个收益值。目标是确定一个作业的执行顺序,使得在不超过任何作业截止时间的前提下,最大化总收益。
证明过程:
1. 证明Job sequencing问题是NP问题
为了证明Job sequencing问题是NP问题,我们需要证明存在一个多项式时间的算法来验证一个给定的作业执行顺序是否是问题的解。
初始化总收益为0,当前时间为0。
遍历给定的作业执行顺序:
如果当前时间超过作业的截止时间,则跳过该作业。
否则,将作业的收益值加到总收益上,并将当前时间更新为作业的执行时间(假设每个作业的执行时间为其收益值,或者为给定的固定值)。
检查总收益是否满足题目要求(例如,是否为最大收益)。
输出:如果总收益满足要求,则输出“是”,否则输出“否”。
由于验证过程可以在多项式时间内完成(遍历作业列表的次数是线性的),因此Job sequencing问题是NP问题。
2. 证明Job sequencing问题至少和某个已知的NPC问题一样难
为了证明Job sequencing问题是NPC问题,我们可以使用归约法,将已知的NPC问题归约到Job sequencing问题。这里我们选择0-1背包问题(0-1 Knapsack Problem)作为已知的NPC问题。
对于0-1背包问题中的每个物品,创建一个作业。作业的截止时间设为背包的总容量,收益值设为物品的价值,执行时间(或“权重”)设为物品的重量。
构造Job sequencing问题的一个实例,其中作业列表就是上面创建的作业,目标是最大化总收益(即背包中物品的总价值),同时确保不超过背包的总容量(即作业的截止时间)。
输出:如果Job sequencing问题有一个解(即一个作业的执行顺序),使得总收益最大化且不超过任何作业的截止时间,那么这个解就对应于0-1背包问题的一个解(即一个物品的选择方案)。
由于归约过程可以在多项式时间内完成(每个物品都映射到一个作业),并且0-1背包问题是NPC问题,因此Job sequencing问题也是NPC问题。
十九、划分问题(Partition)
问题描述:
划分问题(Partition Problem)是一个经典的组合优化问题。给定一个正整数集合S = {a_1, a_2, …, a_n},判断是否存在一个子集S’ ⊆ S,使得子集S’中所有元素的和等于集合S中剩余元素的和。
证明过程
1. 证明划分问题是NP问题
要证明划分问题是NP问题,我们需要证明对于任何给定的划分方案,都可以在多项式时间内验证其是否正确。
验证步骤:
计算S’中所有元素的和sum_S’。
计算集合S中除S’外的所有元素的和sum_S - sum_S’。
检查sum_S’是否等于sum_S - sum_S’。
输出:如果相等,则输出“是”,否则输出“否”。
由于上述验证过程可以在多项式时间内完成(加法和比较操作),因此划分问题是NP问题。
2. 证明划分问题至少和某个已知的NPC问题一样难
我们选择子集和问题(Subset Sum Problem)作为已知的NPC问题来进行归约。子集和问题定义为:给定一个正整数集合A = {a_1, a_2, …, a_n}和一个目标整数T,判断是否存在一个子集A’ ⊆ A,使得A’中所有元素的和等于T。
归约过程:
输入:一个正整数集合A = {a_1, a_2, …, a_n}和一个目标整数T(子集和问题的实例)。
构造:
令S = A ∪ {T}(将目标整数T添加到集合A中)。
计算集合S的总和sum_S。
构造新的目标值target = sum_S / 2(如果sum_S是奇数,则划分问题无解,因为无法将总和均分)。
输出:划分问题的一个实例(S, target)。
现在,如果子集和问题有一个解A’,其和等于T,那么A’ ∪ {T}就是划分问题的一个解,因为(sum_S - T) + T = sum_S,且sum_S / 2是这两个和的共同值。反之,如果划分问题有一个解,那么它也对应于一个子集和问题的解。
二十、最大割(Max cut)

二十一、分团问题(Clique,参考独立集)
问题描述
分团问题(Clique Problem)是一个图论问题,给定一个无向图G = (V, E),其中V是顶点集,E是边集。分团(Clique)是图中的一个顶点子集,其中的任意两个顶点之间都有边相连。分团问题通常指的是寻找图中最大的分团(即包含顶点数最多的分团),这被称为最大分团问题(Maximum Clique Problem)。
证明过程
1.证明分团问题是NP问题
验证解的有效性:给定一个顶点子集C,验证它是否是一个分团是容易的。我们只需要检查C中的任意两个顶点之间是否都存在边。这可以通过遍历C中所有顶点对并检查它们是否在边集E中来完成,这是一个多项式时间操作。因此,验证解的有效性可以在多项式时间内完成,所以分团问题是NP问题。
2.证明分团问题至少和某个已知的NPC问题一样难
我们使用顶点覆盖问题(Vertex Cover Problem)来进行归约。顶点覆盖问题是一个已知的NP完全问题,其中给定一个无向图G = (V, E)和一个整数k,目标是找到一个大小不超过k的顶点子集V’,使得V’中的顶点与图G中的所有边都至少有一个公共端点(即V’是一个顶点覆盖)。
归约过程:
假设我们有一个顶点覆盖问题的实例,即图G = (V, E)和整数k。我们可以构造一个新的图G’,其中G’的顶点集是G的边集E,而G’的边集由G中的顶点导出。具体来说,对于G中的任意两个顶点u和v,如果(u, v)是G中的一条边,则在G’中创建一个顶点e_{uv}。对于G中的任意三个顶点u、v和w,如果(u, v)、(u, w)和(v, w)都是G中的边,则在G’中创建一条边连接e_{uv}、e_{uw}和e_{vw}。
现在,G’中的分团对应于G中的顶点覆盖。具体来说,G’中的一个分团C’(即G’中的一个顶点子集,其中的任意两个顶点之间都有边相连)对应于G中的一个顶点覆盖V’。这是因为C’中的每个顶点e_{uv}都对应于G中的一条边(u, v),而由于C’中的任意两个顶点之间都有边相连,这意味着V’(即C’中所有顶点对应的边的端点集合)是一个顶点覆盖。
此外,G’中的最大分团的大小(即包含的顶点数)等于G中的最小顶点覆盖的大小。因此,如果我们能够解决G’中的最大分团问题,就可以解决原始的顶点覆盖问题。
如果顶点覆盖问题有一个解(即一个大小不超过k的顶点覆盖V’),则根据归约过程,我们可以构造一个G’中的分团C’,其大小等于V’的大小(即等于k),因为C’中的每个顶点都对应于V’中的一个顶点。
反之,如果G’中有一个大小为k的分团C’,则根据归约过程,我们可以构造一个大小不超过k的顶点覆盖V’,因为V’中的每个顶点都是C’中某个顶点对应的边的端点。