本文来自《老饼讲解-BP神经网络》https://www.bbbdata.com/

BP神经网络更原始的名称是"多层线性感知机MLP"，由于它在训练时使用梯度下降算法，并"反向传播Back Propagation Neural"地计算梯度，所以后来也称为BP神经网络。下面讲解什么是BP神经网络的反向传播。

一、什么是BP的反向传播

1.1 什么是反向传播

“反向传播指的是BP神经网络计算参数的梯度时的计算方式”，由于BP神经网络求解时所使用的是梯度下降算法(或其他算法)，这些算法一般都需要利用误差函数对参数的梯度，因此，计算梯度是BP神经网络训练中重要的一部分，而反向传播式地计算梯度就是BP神经网络的特色，BP神经网络之所以叫BP(Back Propagation Neural Network)神经网络，指的正是它计算梯度时这种后馈的特色。

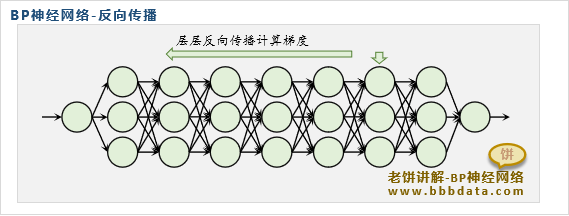
1.2 反向传播的意义

而对于常用的三层BP神经网络的梯度推导，而可以简单地直接求导就可以，甚至不需要涉及到反向传播，反向传播更多是为了多层、深层的BP神经网络而提出的计算方法。反向传播的意义更多是体现在深度学习之中。
三层BP神经网络梯度推导过程：三层BP神经网络梯度推导过程

二、BP神经网络如何通过反向传播计算梯度

如下，是一个K层的BP神经网络：

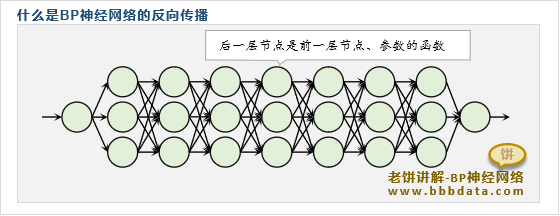
不妨以第k-1层到第k层的参数$p^{(k,k-1)}$为例，分析它的梯度公式是什么
由于第k层节点是关于$p^{(k,k-1)}$的函数，且后一层的节点总是前一层节点的函数
如此一来，$E(p(k,k-1))$可以看成是如下一个超级复合函数：
$$E(p^{(k,k-1)})=E(N^{(K)}(...(N^{(k+1)}(N^{(k)}(p^{(k,k-1)}))))$$
因此对于$p^{(k,k-1)}$的梯度，根据复合函数的链式求导，则有：
$$\frac{\partial E}{\partial p^{(k,k-1)}}=\sum _{i_K}\frac{\partial E}{\partial N_{i_K}^{(K)}}\sum _{i_{K-1}}\frac{\partial N_{i_K}^{(K)})}{\partial N_{i_{K-1}}^{(K-1)}}\sum _{i_{K-2}}\frac{\partial N_{i_{K-1}}^{(K-1)})}{\partial N_{i_{K-2}}^{(K-2)}}....\sum _{i_k}\frac{\partial N_{i_k}^{(k)})}{\partial p^{(k,k-1)}}$$

三、BP梯度公式解读

看着头很晕，但粗略可以看出，它分为三块：

1. 先由误差函数求出最后一层的节点梯度
2. 不断地求后一层节点对前一层的节点梯度，直到所要求的参数所在的节点
3. 最后求出节点对参数的梯度就可以

可以看出，整个梯度的计算过程由误差函数开始，不断地后馈到前一层节点，最后传播到参数上
而这种后馈的特性，给求解梯度带来了非常大的便利性，它的计算过程如下：

• 先算出最后一层节点的梯度，再后馈式逐层传播到每一层的节点
• 每当算出某层节点的梯度时，就马上计算当层的参数，如此迭代就可以

---

相关链接：

《老饼讲解-机器学习》：老饼讲解-机器学习教程-通俗易懂
《老饼讲解-神经网络》：老饼讲解-matlab神经网络-通俗易懂
《老饼讲解-神经网络》：老饼讲解-深度学习-通俗易懂