1.神经元模型

1.1 M-P神经元模型

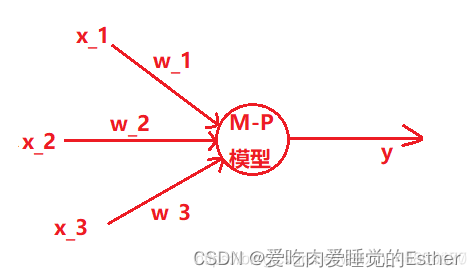
输出函数：

其中θ为阈值，
ω i为第i个神经元的连接权重， xi为来自第i个神经元的输入。

1.2 激活函数

阶跃函数：
理论上我们使用阶跃函数。将输入值映射为输出值为0/1，显然1为神经元兴奋，0为神经元抑制
函数：


Sigmoid函数
因为阶跃函数不连续，所以我们使用替代品sigmoid函数(有时候又称为挤压函数)：
函数：


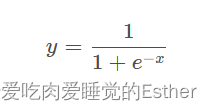
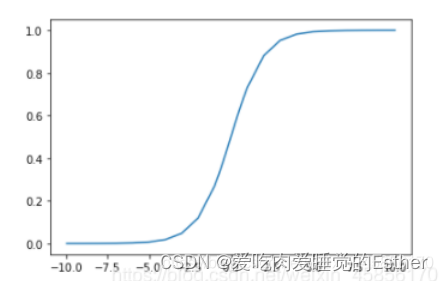
可以看到当sigmoid的输入很大或很小时，其梯度几乎趋近于0。

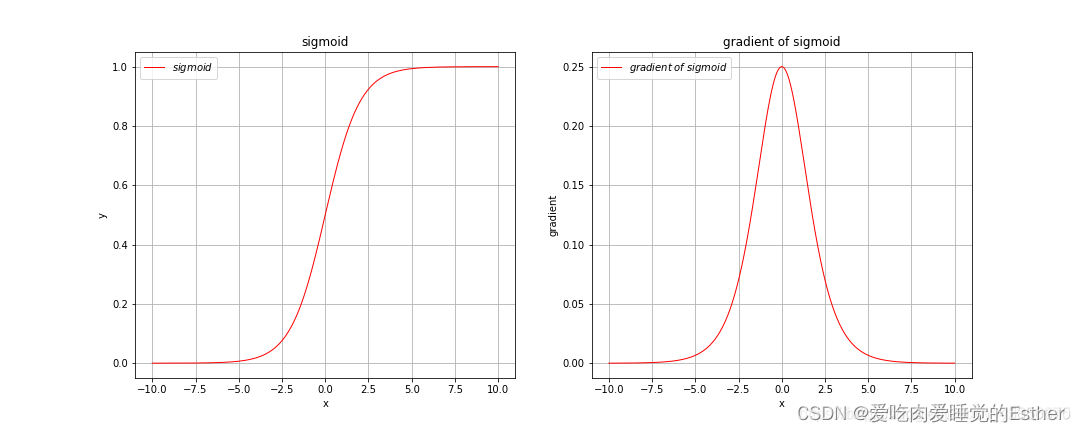
再来看tanh激活函数，
函数为：

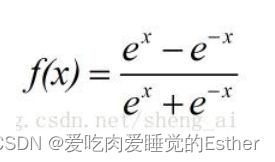
如下图所示：

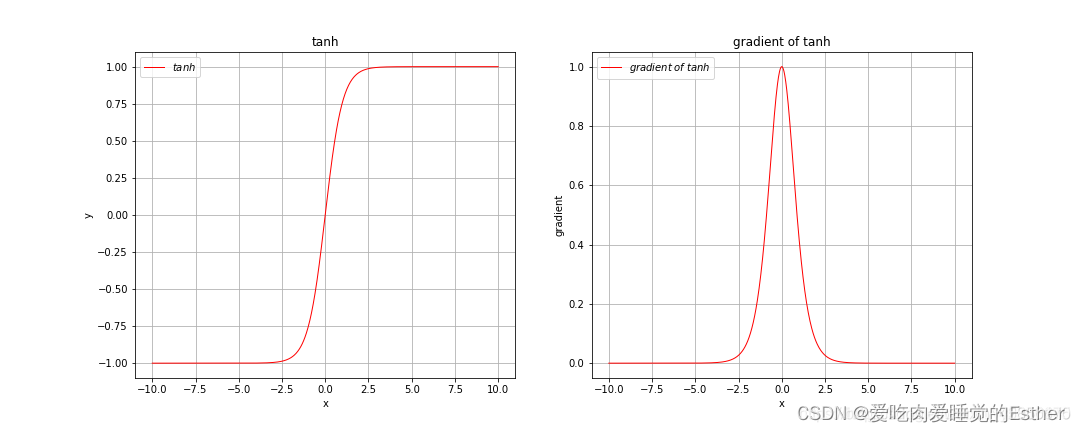
由上图可以看出，tanh激活函数和sigmoid激活函数非常相似，只不过tanh激活函数将输入值压缩到了-1到1之间，由其梯度图像可以看出，当输入很大或很小时梯度也是趋于0的。
最后让我们来看一下relu激活函数
函数为：

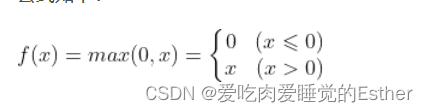
如下图所示：

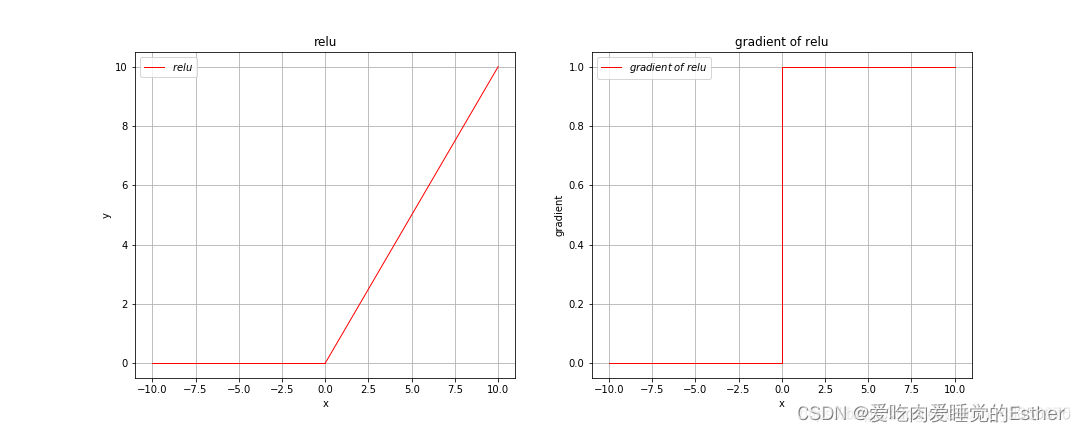
从上图中可以看出，relu激活函数在0到正无穷上会随着输入的增大而无限增大，在小于0的区间上其值全为0，但是我们还可以看到其梯度在0到正无穷上永远为1。

由于神经网络最后对于损失函数的优化也是使用梯度下降，因此在实际运用中，我们基本上会经常用relu激活函数，因为sigmoid激活函数以及tanh激活函数从上面的图像中已经可以看出，其存在梯度消失的问题，我们知道，当我们使用梯度下降去优化某个损失函数时，是需要求梯度的，但是如果输入过大（可能初始化权重过大，也可能特征过大）并且采取的是sigmoid或tanh激活函数，那么当我们在输入位置求取梯度时其梯度值趋近于0，而我们对于参数的更新量也趋近于0，因此最终会因为梯度消失的问题造成收敛过慢，因此我们会使用relu激活函数来加快收敛速度，但relu激活函数的精度不如sigmoid激活函数。

2.感知机与多层神经网络

2.1 感知机

感知机由两层神经元构成，输入层接受外界信号后传递给输出层，输出层为M-P神经元，亦称“阈值逻辑单元”
从几何角度来说，给定一个线性可分的数据集T，感知机的学习目标是构筑一个在n维空间将数据集T中正负样本完全正确划分的超平面，其中wT-sita为超平面方程,
训练逻辑：
对训练样例(x,y)，若当前感知机的输出为y^，则这样调整:

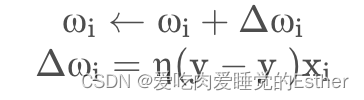
其中 η∈(0,1)称为学习率，若预测正确则不调整，若错误，则根据错误的程度进行调整。

2.2 多层前馈神经网络

单隐层前馈神经网络

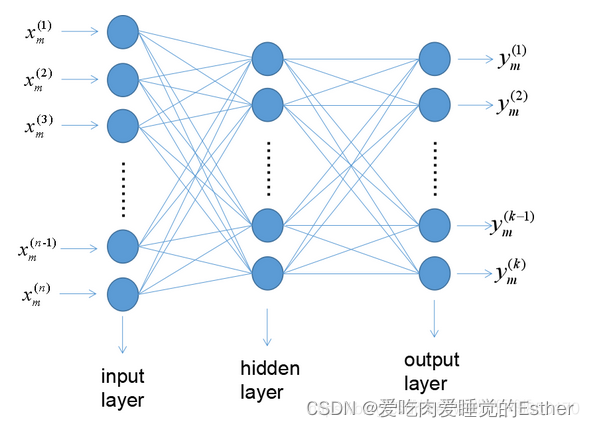
优秀笔记：多层感知机与神经网络学习总结

3.误差逆传播算法（BP算法）

原理视频：【算法思想】14分钟了解BP神经网络
线性回归更新算法：

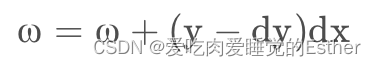
个人理解：本算法首先关键字是逆向，及由预测结果的错误程度去反馈，去修改 ω 的值(注ω可以为常数也可为矩阵)，
算法推导：