分类问题的基本概念

分类问题概述：对于给定的一个对象，根据其特征将其划分到多个已给定的类别中的一个。

二分类和多分类：给定的类别有多少个就是几分类。如果有两个类别则称为二分类，如果有多个（两个以上）类别则称为多分类。

分类问题的预处理-创建虚拟变量：

• 必须的预处理：创建虚拟变量的过程也就是将分类变量转换成数字进行表示。这是处理分类问题必须的数据预处理过程。
• SPSS创建虚拟变量：

打开SPSS并导入数据后如图所示点击：转换→创建虚变量

在如下所示的窗体右上方选择需要创建虚拟变量的分类变量，下方根名称处填写虚拟变量的名称。选择需要创建虚拟变量的变量→给虚拟变量组命名

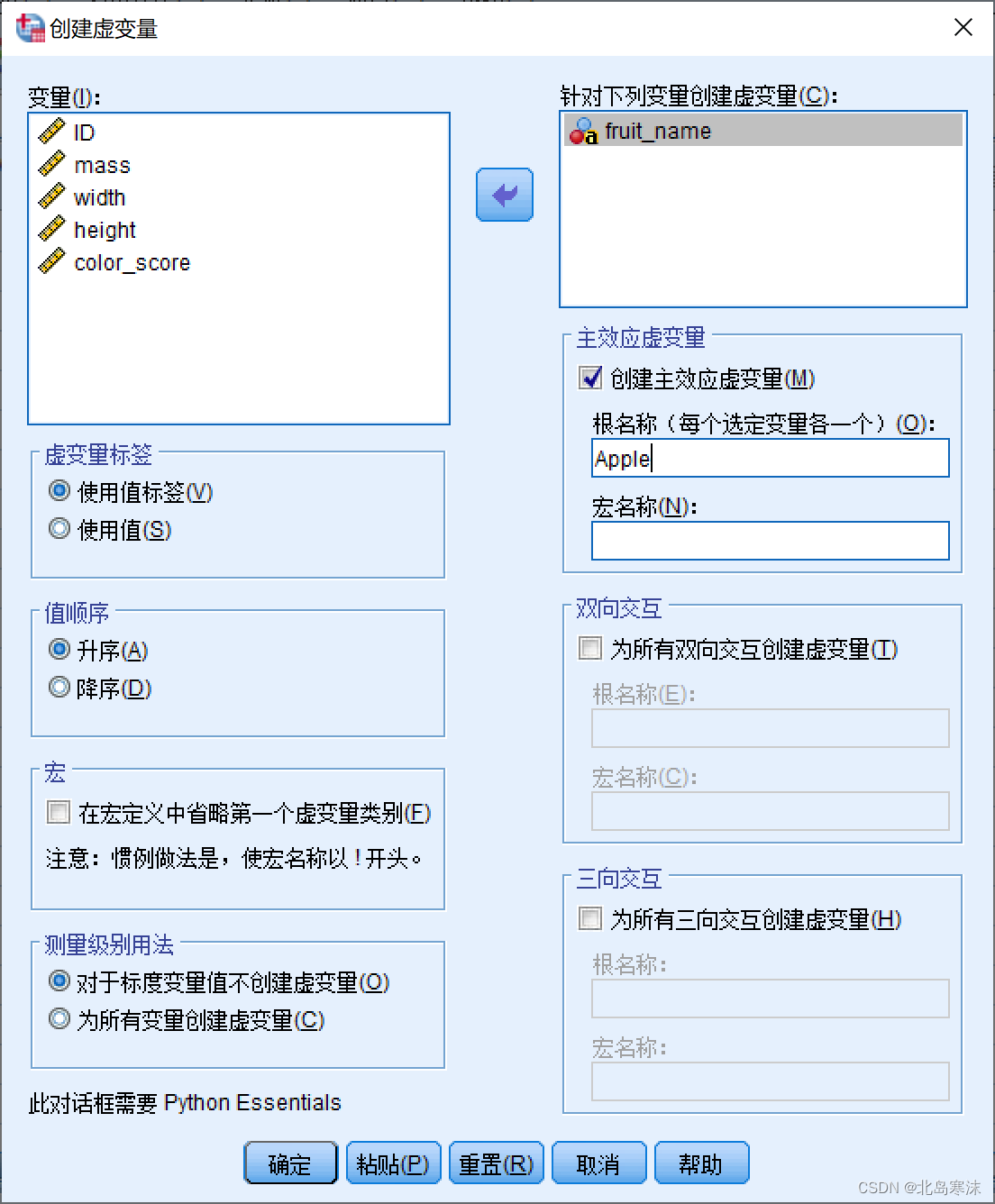
最后，分类变量可以取多少个值，就会生成多少个虚拟变量，每个虚拟变量占据新的一列。

清除掉多余的虚拟变量，并给保留的虚拟变量重命名。清除过程略，给虚拟变量重命名只需要打开左下角的变量视图，然后在里面双击变量名修改即可。

逻辑斯蒂回归（Logistic）

逻辑回归模型的基本思想：把因变量视为分类变量的概率，大于0.5表示事件发生，否则认为事件不发生。由此得到的模型称为线性概率模型（LPM）。线性概率模型的基本形式与多元线性回归模型的基本形式相同。但是由于因变量的取值范围只能是[0,1]，因此需要借助连接函数将因变量的范围进行压缩。

连接函数：常用的连接函数有两种，分别是标准正态分布的累积密度函数和Sigmoid函数，分别对应的两种回归方式是Probit回归和逻辑斯蒂回归。但是由于逻辑斯蒂回归有解析表达式，所以该模型更加方便。

逻辑斯蒂模型的求解方法：模型可以通过极大似然估计法进行参数求解。

SPSS建立并求解逻辑斯蒂回归模型：

1.打开SPSS并导入数据，依次点击：分析→回归→二元Logistic

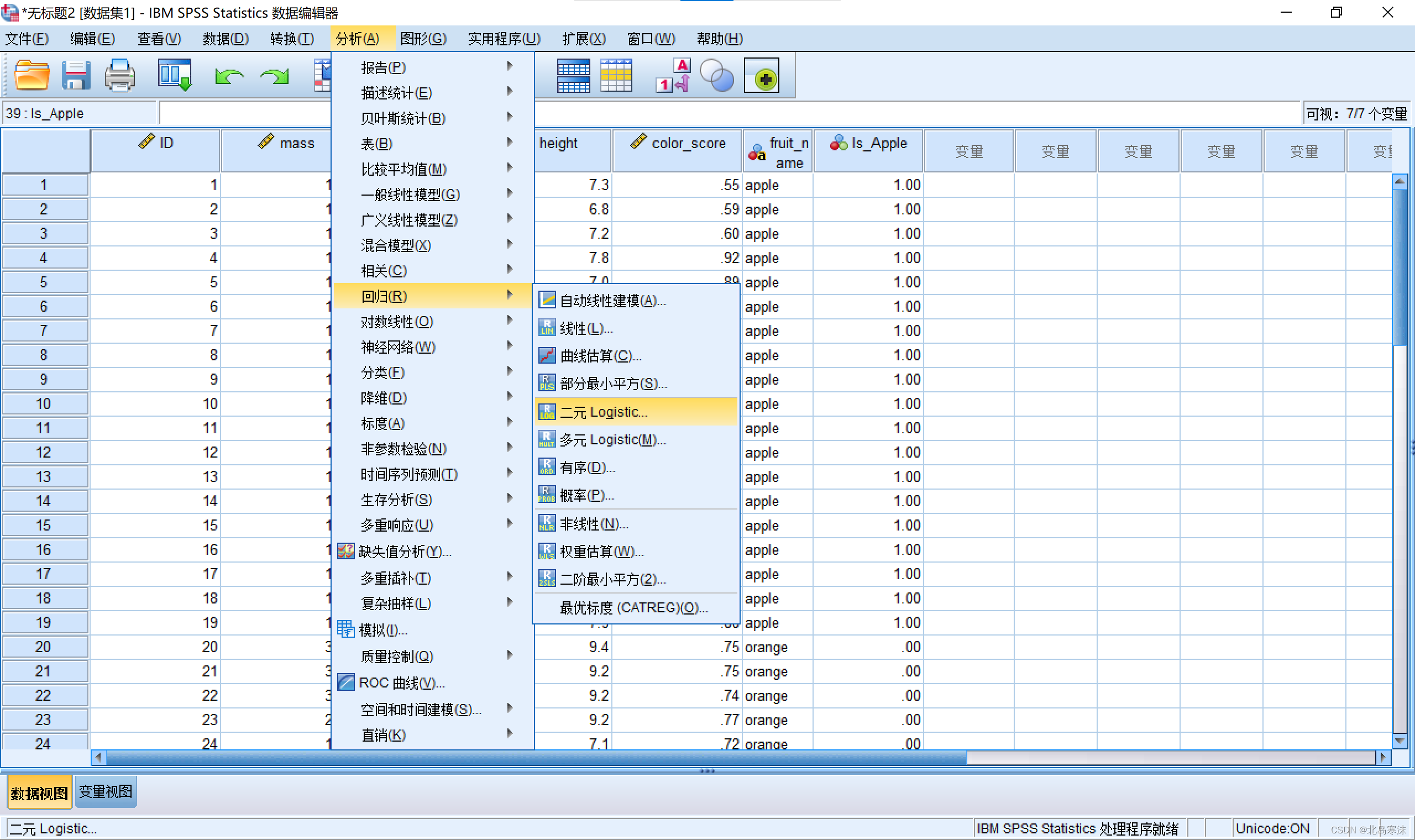
2.在新窗体中分别选择好因变量和协变量，其中协变量就是指自变量。窗口中的”方法“部分可以选择回归的方法，具体选择哪个没有确定的准则，可以都尝试一下。

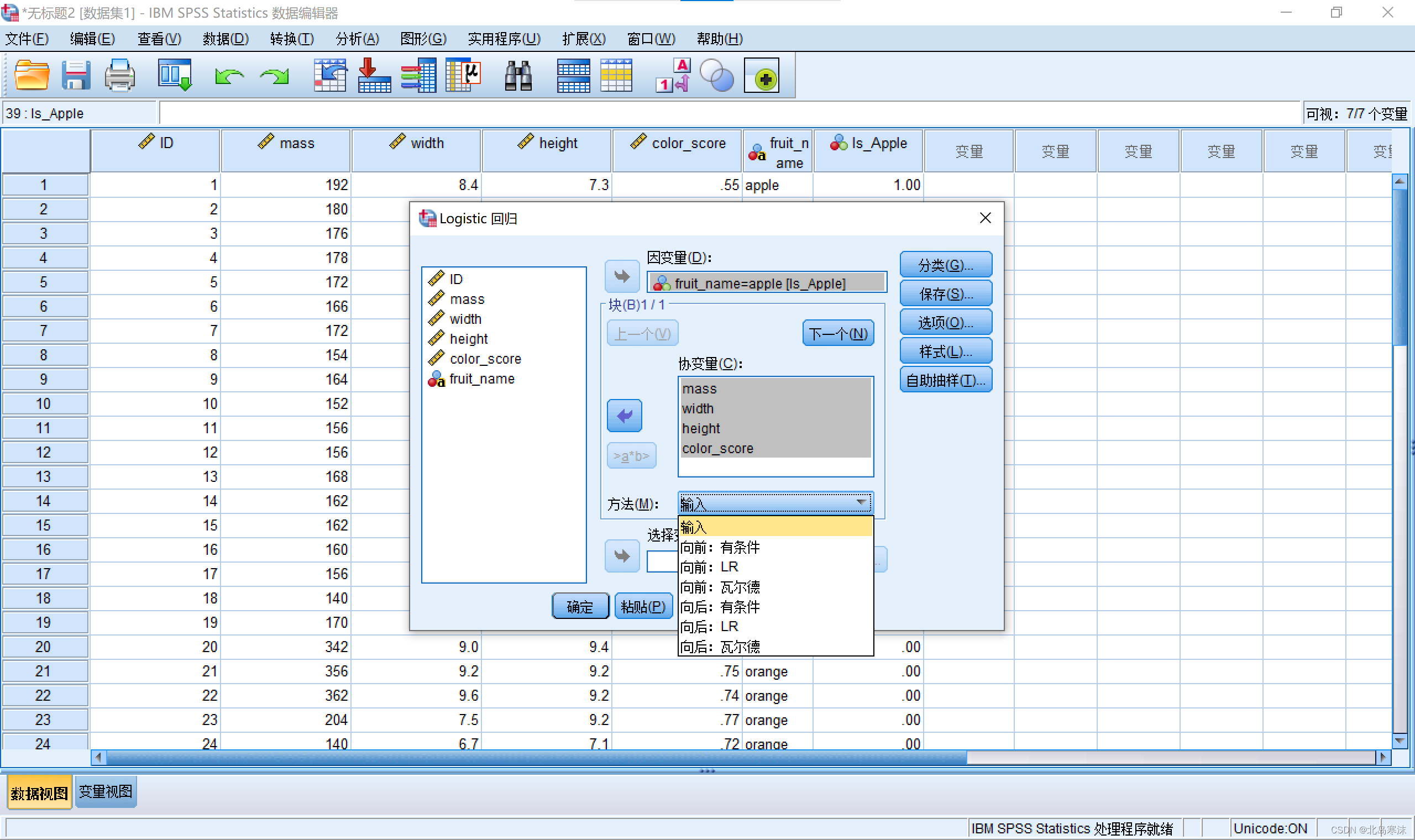
3.如果自变量中存在定性变量且没有手动生成虚拟变量，则需要点击窗体右边的“分类”按钮，在如下所示的窗体中将定性变量移动到右边。

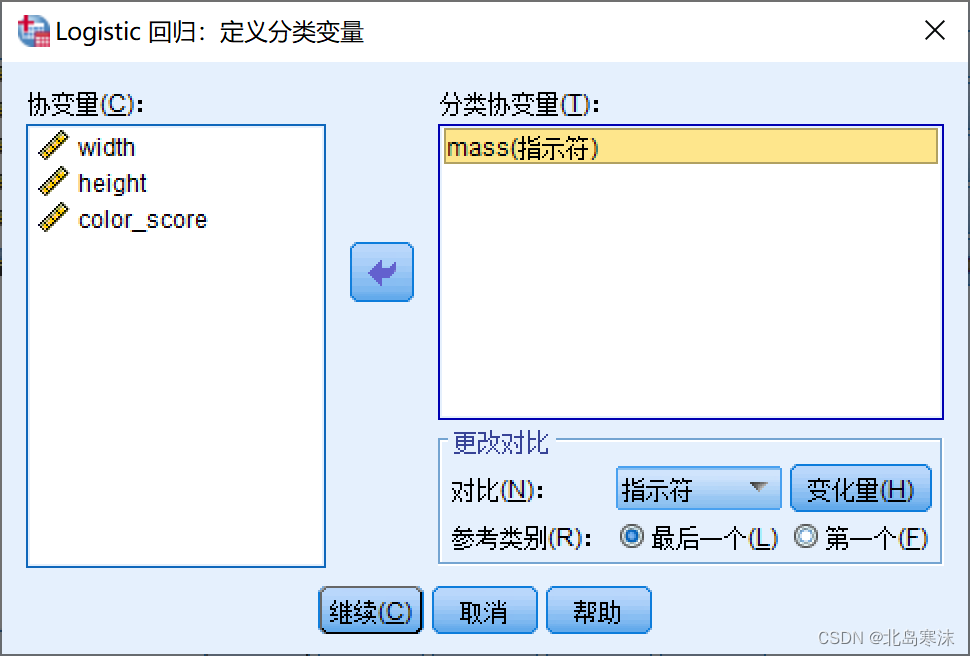
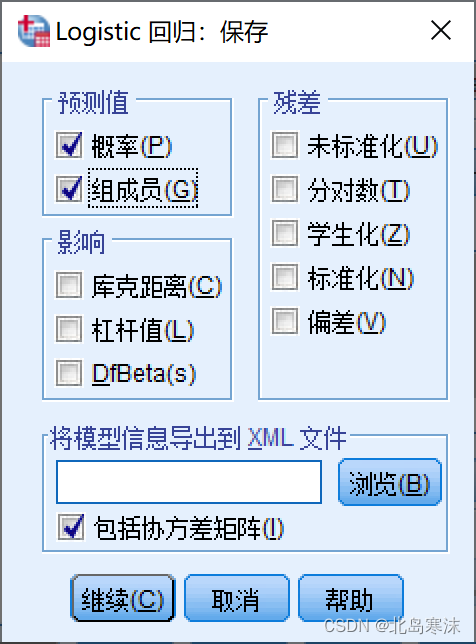
4. 保存选项中对应需要输出并放在原始表格中的结果。

• 概率：表示逻辑斯蒂回归模型函数求解出的预测值，是一个小数。
• 组成员：表示逻辑斯蒂回归模型的分类结果。
  

5.在“选项”按钮菜单中可以设置最大迭代次数和分类临界值。分类临界值一般设置为0.5（默认），增大最大迭代次数高可能会提高模型准确率。

6.“自助抽样”方法是指在样本数很少的情况下通过对原始样本的重复使用来扩大样本集，一般不使用。

SPSS逻辑斯蒂回归结果解读：

• 分类表：表示各类的预测正确率。
  
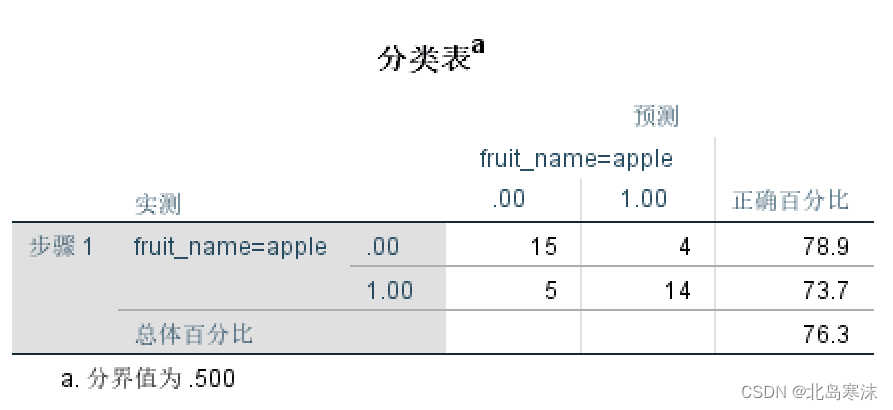
• 方程中的变量：表示逻辑斯蒂回归模型的各个回归系数（B所在列）以及对应的显著性。一般认为显著性小于0.05的是显著的，因此width height和 color_score是显著的。

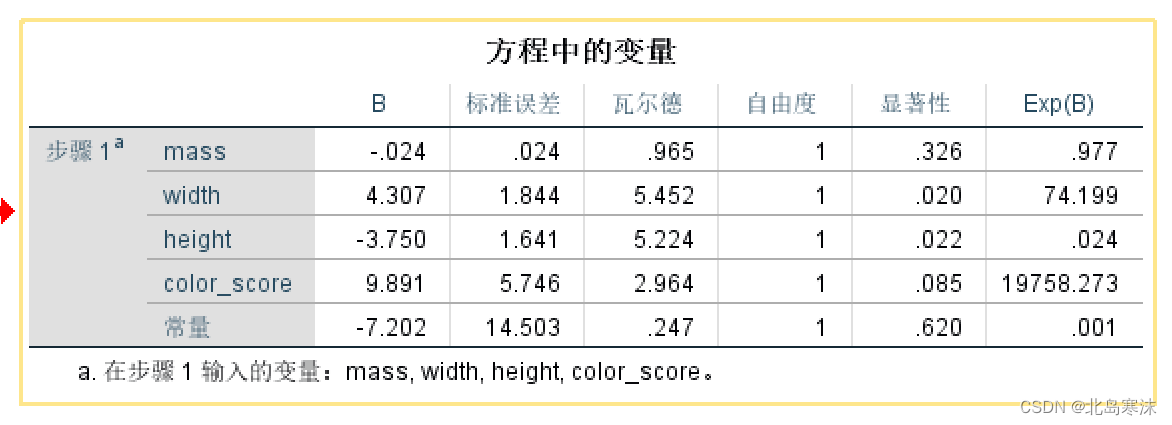
逻辑回归模型预测成功率低的优化方法：在原始模型中增加自变量，自变量可以是原始自变量的平方项、交互项等。但是这种方法可能会导致过拟合问题，需要使用交叉验证进行检验。

SPSS增加自变量的方法：

• 打开导入了数据的SPSS表格，依次点击：转换→计算变量

• 在新的窗体中定义新自变量的名称和计算公式：
  

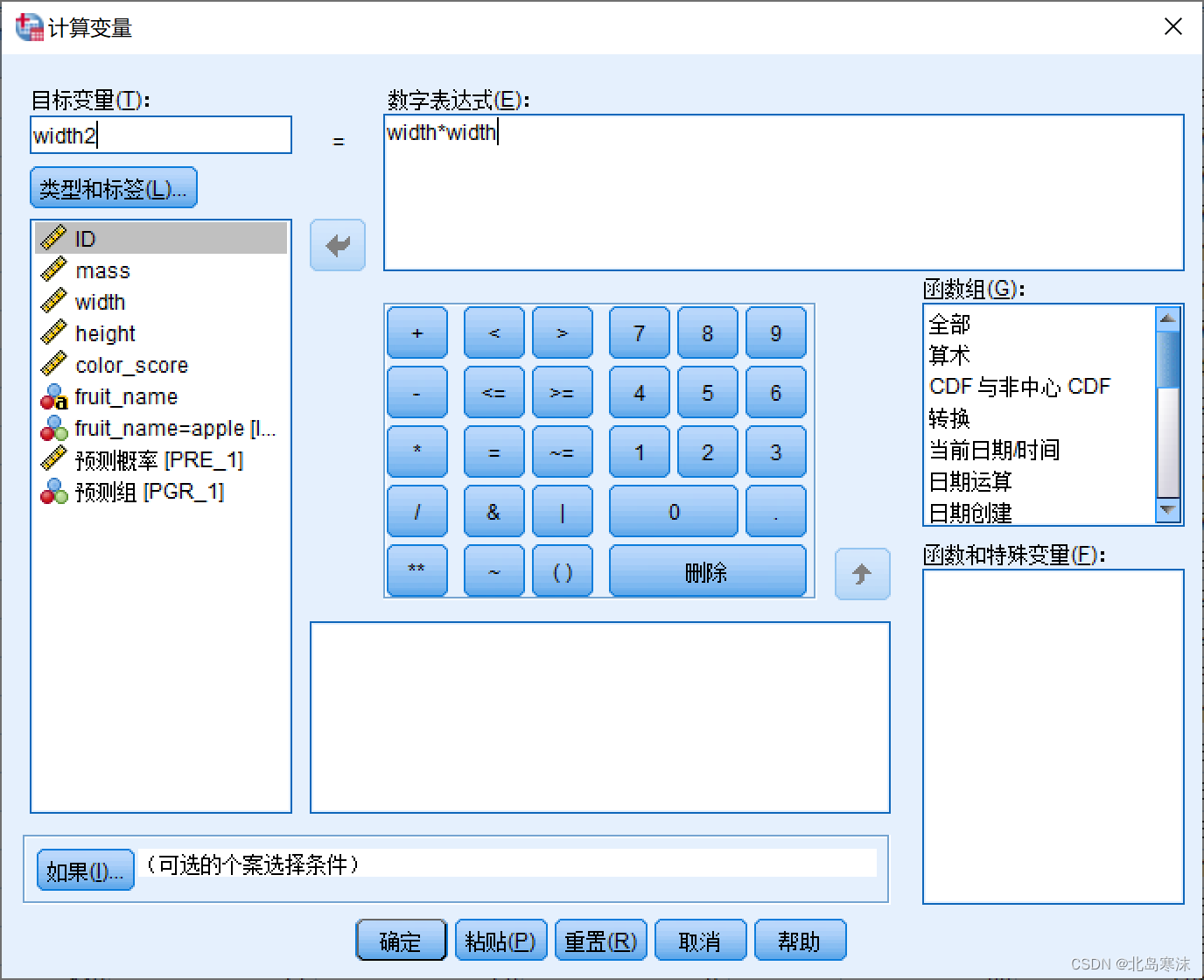
Fisher线性判别分析

Fisher线性判别分析基本思想：给定训练集样例，设法将样例投影到一维的直线上，使得同类样例的投影点尽可能接近和密集，不同类投影点尽可能远离。

SPSS进行Fisher线性判别分析：

1.打开导入了数据集的SPSS软件，依次点击：分析→分类→判别式

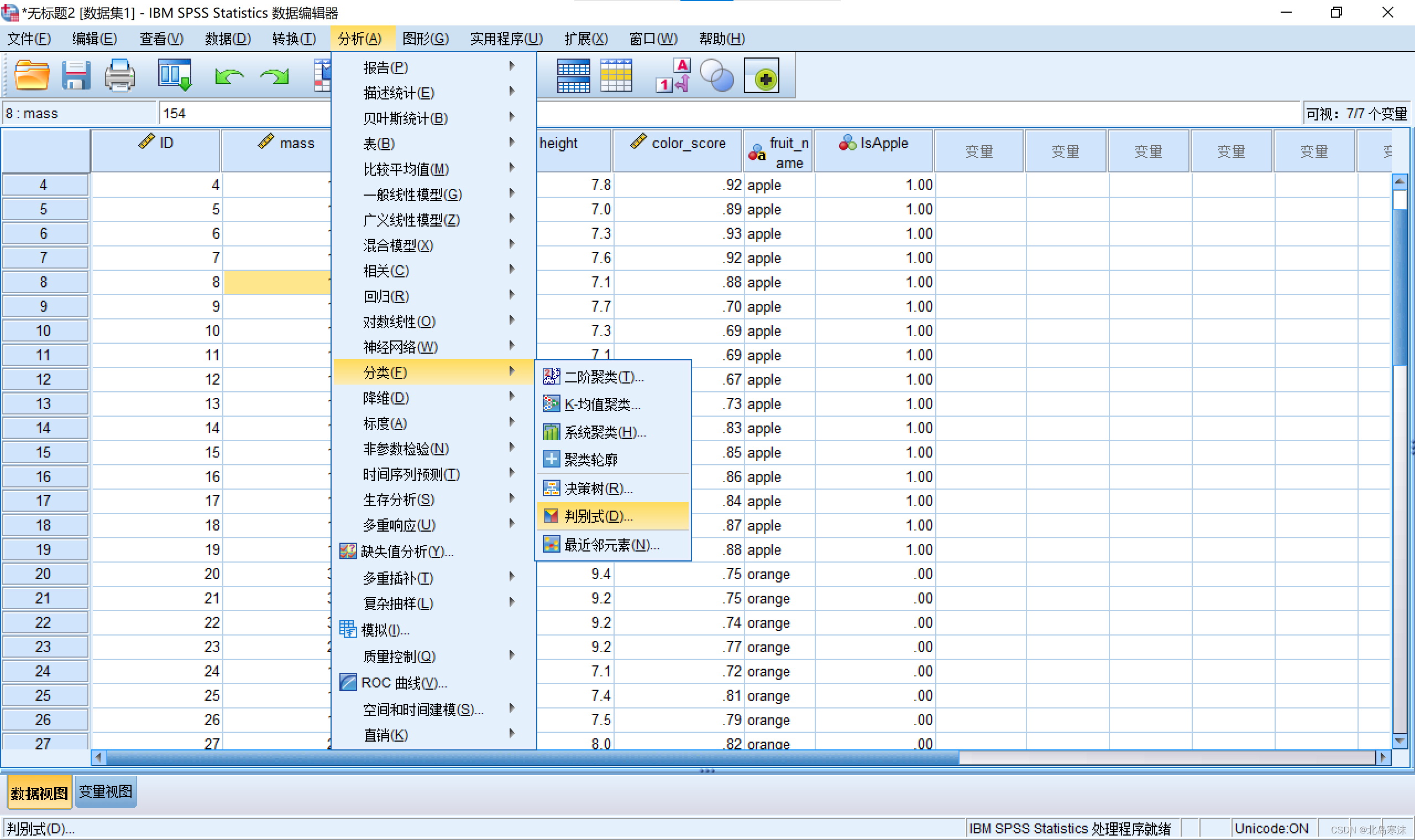
2.选择因变量和自变量，过程与逻辑斯蒂回归模型的使用类似。但是，需要给因变量定义范围。

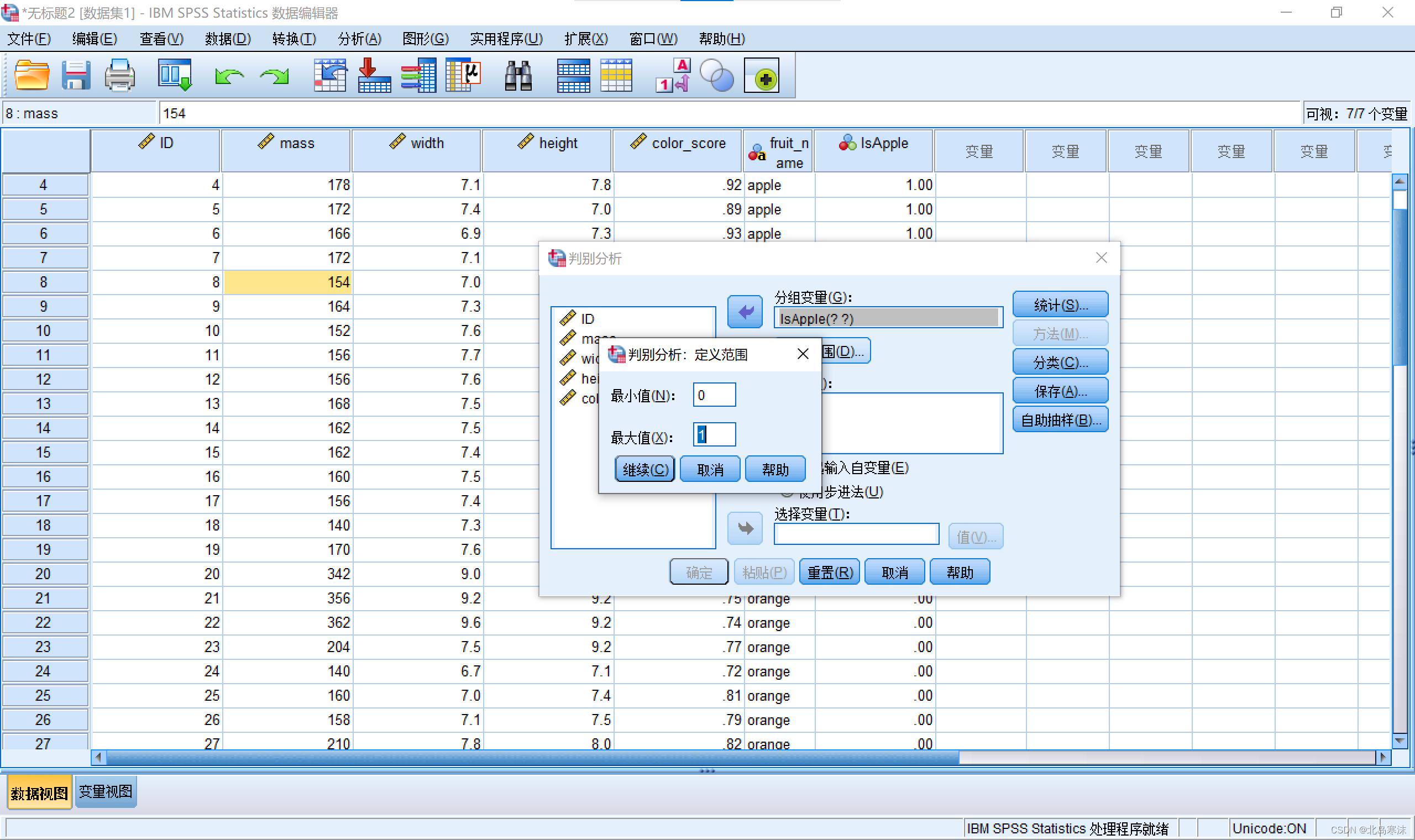
3.在”统计“按钮菜单中，勾选”费希尔“和”未标准化“。

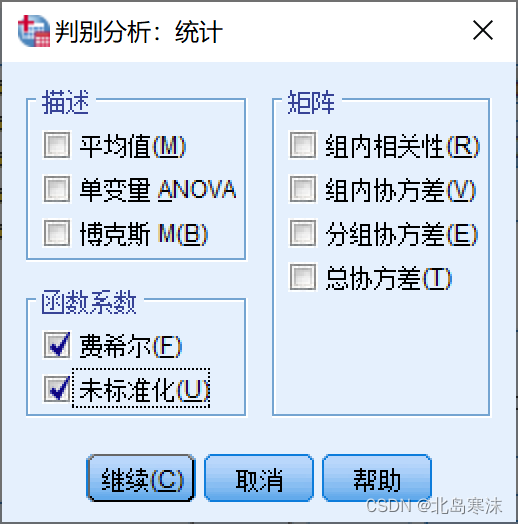
4.在“分类”选项菜单中勾选摘要表，用于记录分类结果。

5.在“保存”按钮菜单中勾选预测组成员和组成员概率。

SPSS进行Fisher线性判别分析的结果：

• 典型判别函数系数表：

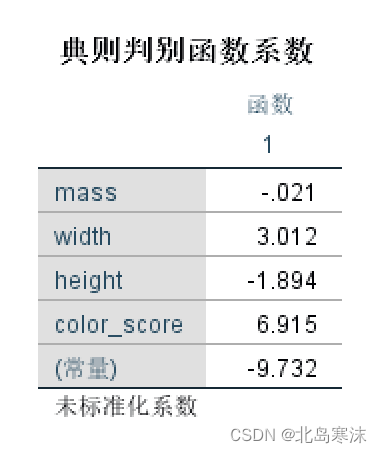
• 分类结果表格：记录了分类的准确率等信息。

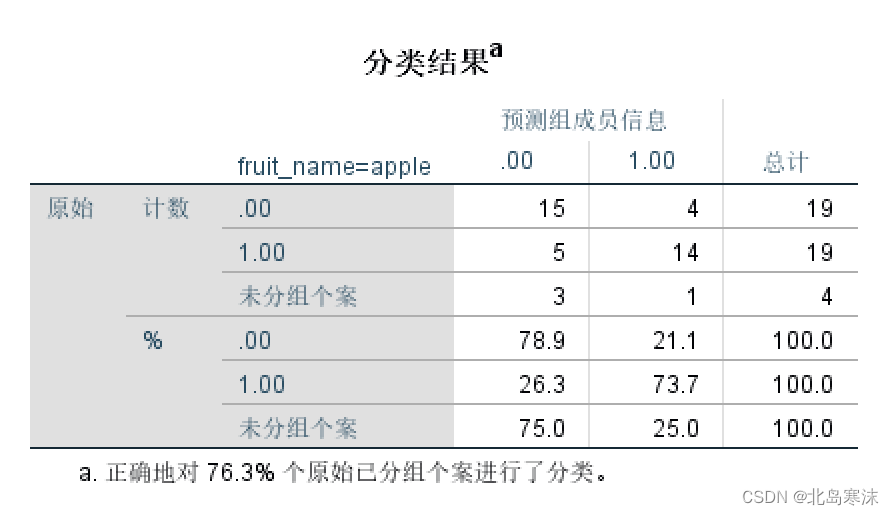
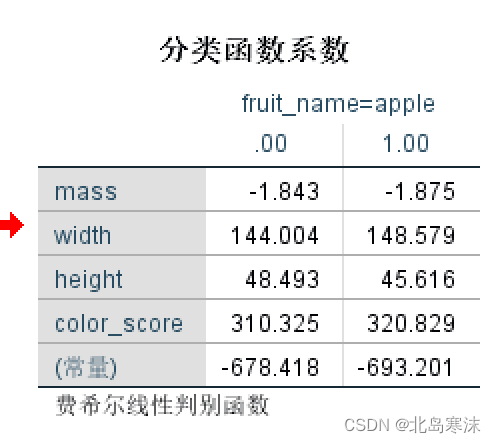
• 分类函数系数：也称为贝叶斯判别函数系数。可以将各个样本的参数代入不同类的分类函数，所得到的函数值最大的一类就是该样本的分类结果。

多分类问题的SPSS求解

使用Fisher线性判别分析求解多分类问题：在求解二分类问题的基础上，修改因变量的取值范围即可。

使用逻辑斯蒂回归求解多分类问题：将Sigmoid函数推广到Softmax函数即可用于逻辑斯蒂的多分类问题。在SPSS中依次点击：分析→回归→多元Logistic

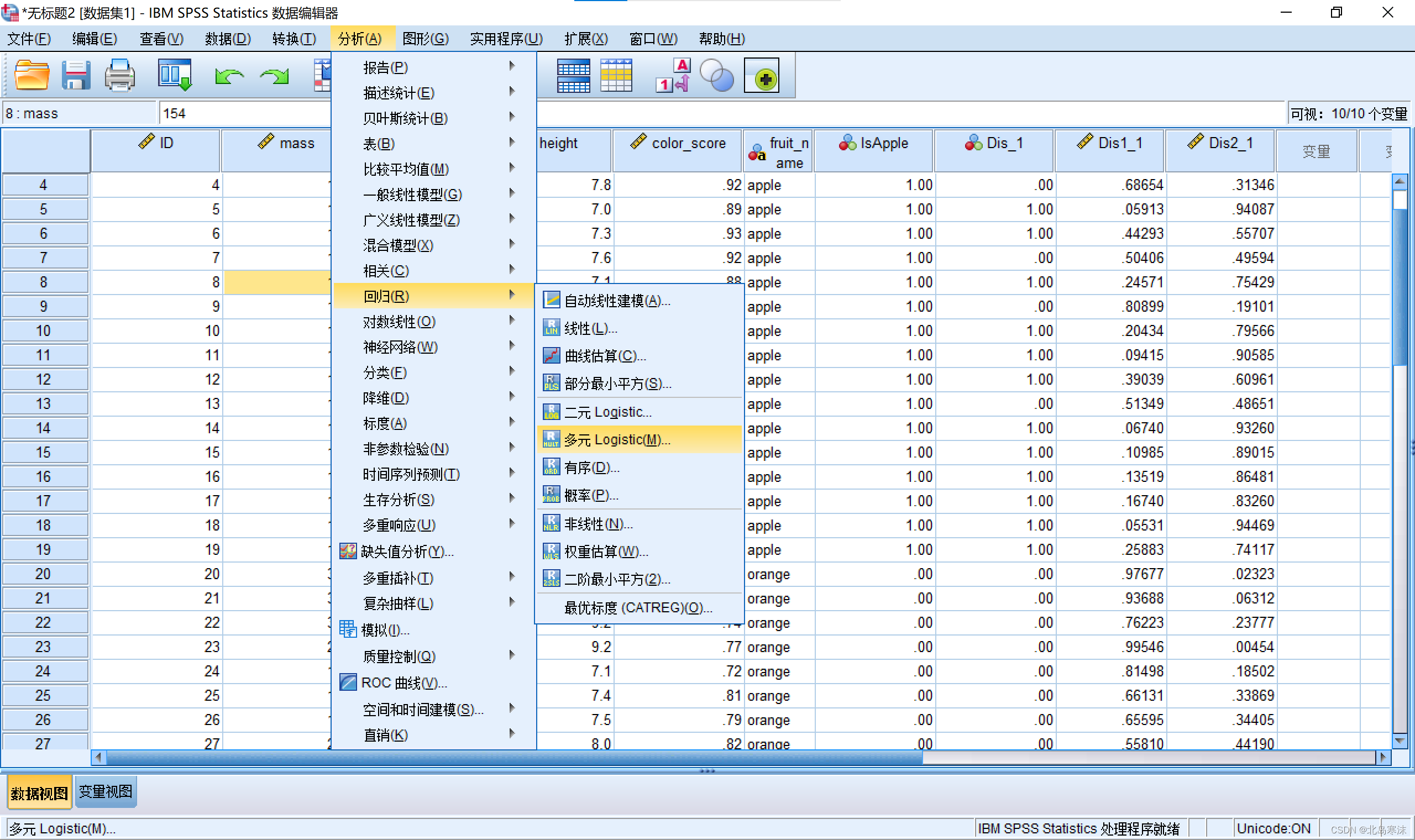
使用方法和二元Logistic方法类似。