一. 树表示法
1.双亲表示法
(1).含义
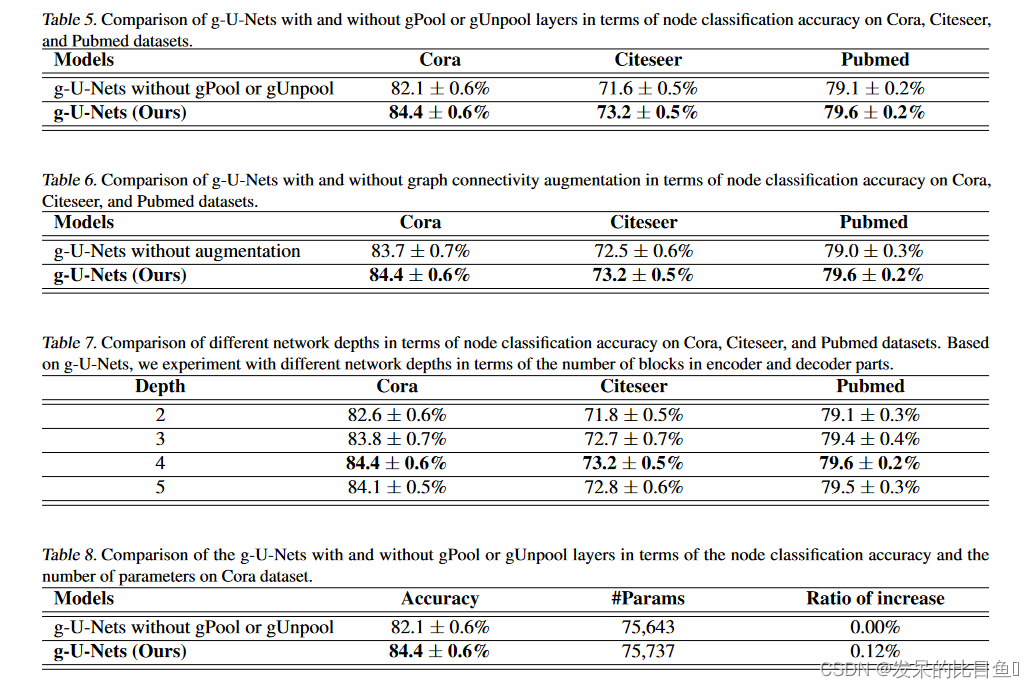
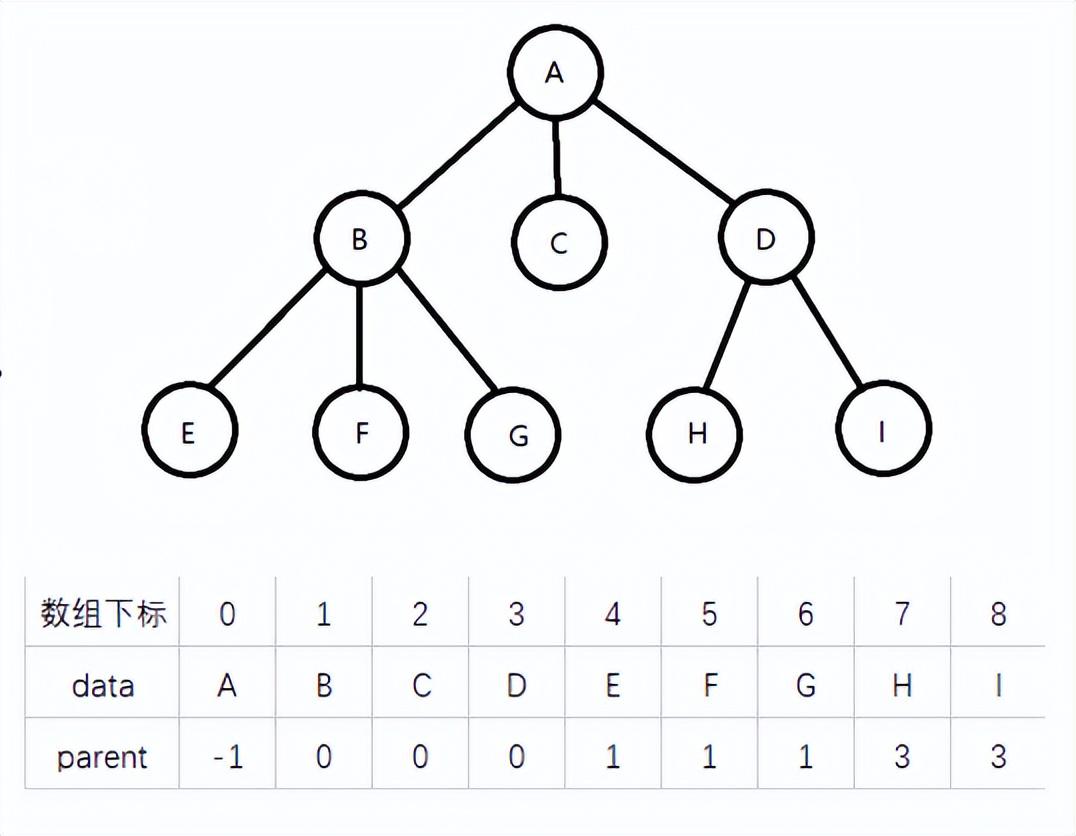
在一棵树中,任意一个结点的双亲只有一个,这是由树的定义决定的。双亲表示法就是利用了树的这个性质,在存储结点信息的同时,在每个节点中附设一个指向其双亲的指针, 指向双亲在链表中的位置。这种结构一般借助数组来实现。这样的链表也称为静态链表。
(2).实现思路
在双亲链表表示法中,根节点没有双亲,其parent指向-1,其余结点的parent指针为存放其双亲结点的数组下标值。双亲表示法简单,易懂,易实现,求指定结点的双亲和祖先非常方便,但是要求某个结点的孩子和兄弟,需要遍历整个数组。
2.孩子表示法
(1).含义
树的每个节点都有自己的孩子,孩子表示法是指在树的每个节点中设置指针指向该节点的孩子。由于一般树中的结点可能存在多个孩子,因此需要链表依次存储结点的所有孩子。孩子链表的存储结构需要同时使用数组和单链表实现。
(2).实现
孩子链表最左边是结点在数组中的索引,中间一列表示结点的数据,最后一列是指向孩子链表的指针,孩子链表使用单链表实现,里面存放的并不是结点本身,而是结点在数组中的索引。与双亲链表相反,孩子链表表示法便于实现涉及孩子及子孙的操作,但不利实现与双亲有关的操作。

3. 双亲孩子链表表示法
(1).含义
树的孩子双亲表示法结构如图,它增加了一个列用于存放结点的双亲在数组中的索引。双亲孩子链表表示法在实际操作中,无论是查找节点的孩子,还是双亲或是遍历整棵树都很容易实现。

4.孩子兄弟表示法
(1).含义
孩子兄弟表示法是一种二叉树表示方法,即用二叉链表作为树的存储结构。与二叉树的二叉链表表示所不同的是,这里的二叉链表节点指针不在去指向左、右孩子,而是指向该结点的第一个孩子(FirstChild)和下一个兄弟节点(NextSibling)
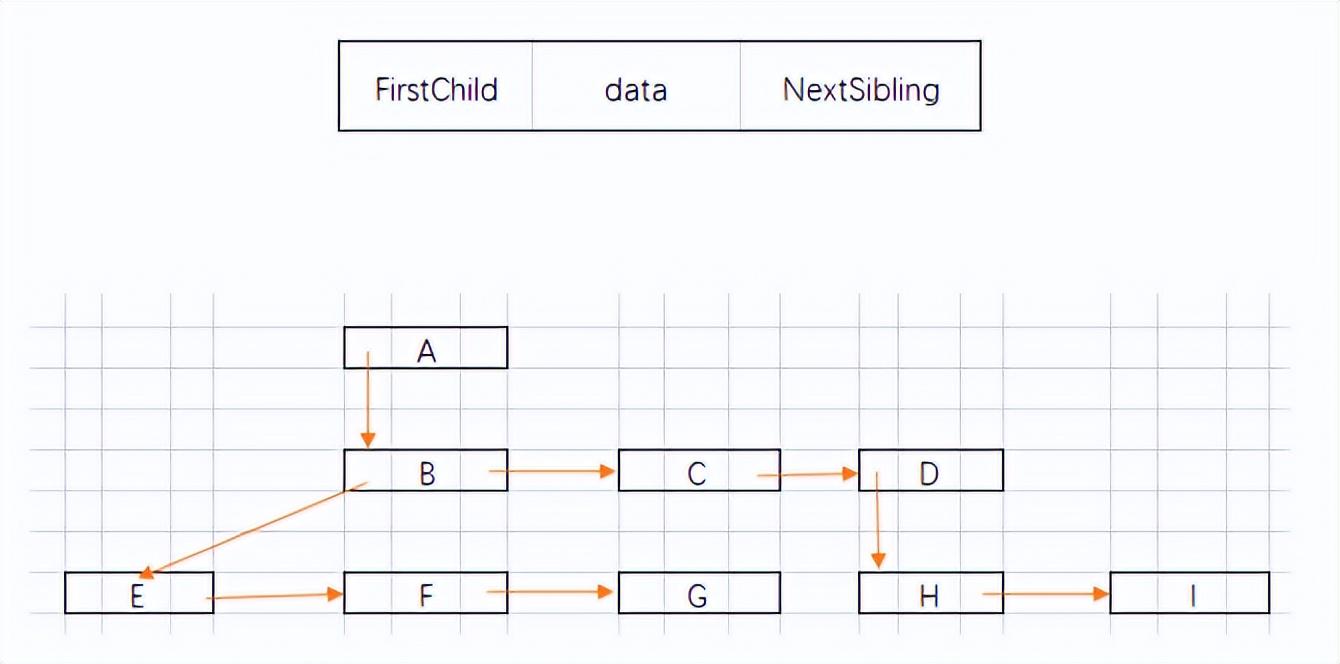
二. 森林
孩子兄弟链表表示法来存储树,实际上使用二叉链表的形式来存储的。而森林是树的有限集合,他也可以用二叉树来表示。可见,树,二叉树,森林之间存在着确定的关系,而且可以相互转换。
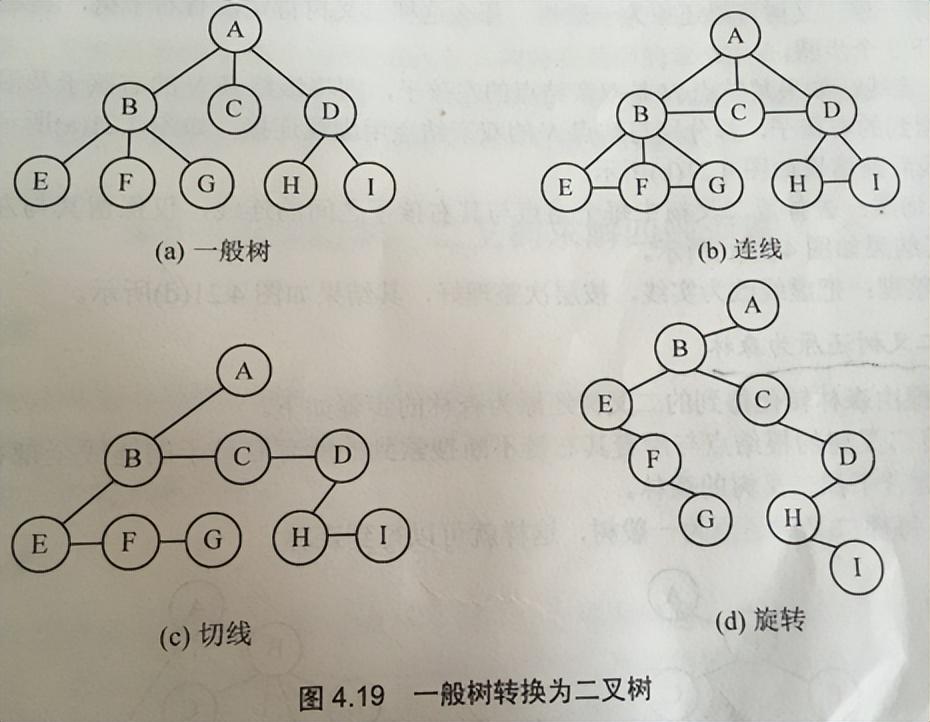
1.一般树转为二叉树
(1). 连线:在所有兄弟节点之间加一条连线
(2). 切线:对于每个结点,除了保留与其最左孩子的连线外,去掉该结点与其他孩子的连线。
(3). 旋转:将所有水平方向的连线顺时针旋转45度
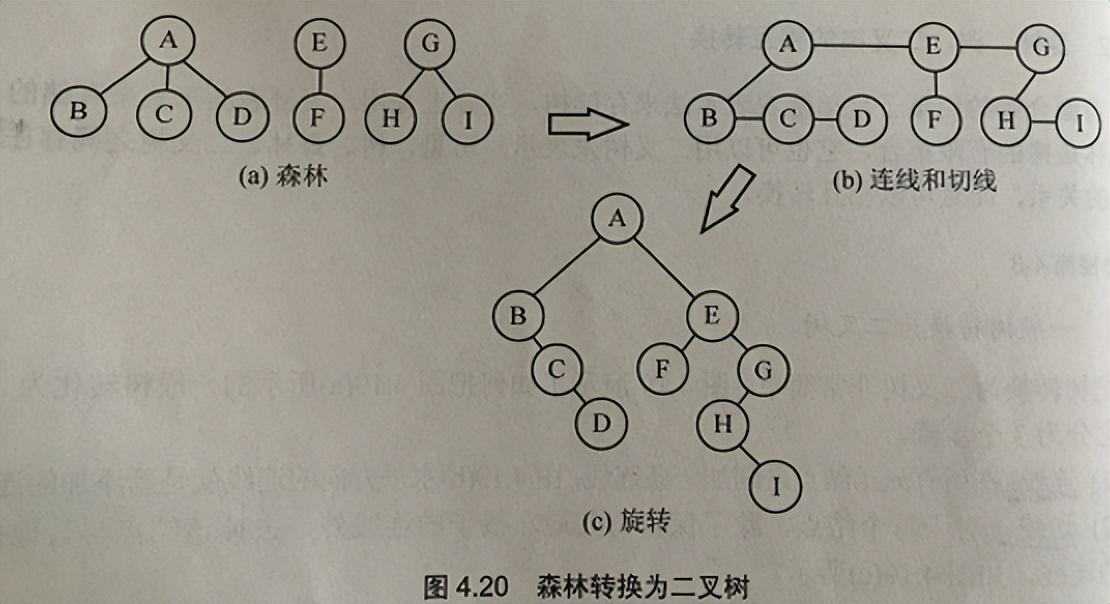
2. 森林转为二叉树
森林是树的集合,把森林转换为二叉树的方法是:现将森林中每一棵树转换为二叉树,然后将二叉树的根节点作为兄弟连在一起。
3. 二叉树还原为一般树
如果一棵二叉树可以还原为一般树,那么这个二叉树肯定没有右子树,其还原过程也分三个步骤:
(1). 连线:如果某结点N是双亲节点的左孩子,则将该结点N的右孩子及其沿着其右链不断搜索到右孩子,都分别与结点N的双亲结点用虚线连接。
(2). 切线:去掉原二叉树中每个结点与其右孩子之间的连线,仅保留与其左孩子之间的连线。
(3). 把虚线改为实线,按照层次整理好。

4. 二叉树还原成森林
(1). 将二叉树的根节点与沿着其右链不断搜索得到的所有右孩子的连线全部抹去,这样就得到包含若干棵二叉树的森林。
(2). 每棵二叉树还原为一般树,这样就可以得到森林。
更多C++后台开发技术点知识内容包括C/C++,Linux,Nginx,ZeroMQ,MySQL,Redis,MongoDB,ZK,流媒体,音视频开发,Linux内核,TCP/IP,协程,DPDK多个高级知识点。
C/C++Linux服务器开发高级架构师/C++后台开发架构师免费学习地址
【文章福利】另外还整理一些C++后台开发架构师 相关学习资料,面试题,教学视频,以及学习路线图,免费分享有需要的可以点击领取
三. 森林遍历
1. 含义
以某种方式访问树中的每一个结点,且仅访问一次。
2. 分类
(1).先根遍历:若树非空,则先访问根结点,再按照从左到右的顺序遍历根结点的每一棵子树。这个访问顺序与这棵树对应的二叉树的【先序遍历】顺序相同。
(2).后根遍历:若树非空,则按照从左到右的顺序遍历根结点的每一棵子树,之后再访问根结点。其访问顺序与这棵树对应的二叉树的【中序遍历】顺序相同。
案例:

森林的先根遍历:A-B-C-D-E-F-G-H-J-I
二叉树森林的先序遍历:A-B-C-D-E-F-G-H-J-I(相同)
完整二叉树的先序遍历:A-B-C-D-E-F-G-H-J-I (相同)
森林的后根遍历:B-C-D-A-F-E-J-H-I-G
二叉树森林的后序遍历:D-C-B-A-F-E-J-I-H-G
完整二叉树的后序遍历:D-C-B-F-J-I-H-G-E-A(不同于二叉树森林的后序遍历)
二叉树森林的中序遍历:B-C-D-A-F-E-J-H-I-G(与森林的后根遍历相同)
完整二叉树的中序遍历:B-C-D-A-F-E-J-H-I-G(与森林的后根遍历相同,自然也与二叉树森林的中序遍历相同
四. 二叉树求解四则运算
1. 目标
将四则运算 3+2*9-16/4 转换成二叉树的表现形式。
PS:这里我们在设计算法的时候只考虑最简单的四则运算,不考虑括号,开方,求余等。
2. 特点
操作数字都是叶子结点, 运算符都是内部结点,优先运算符都在下面。
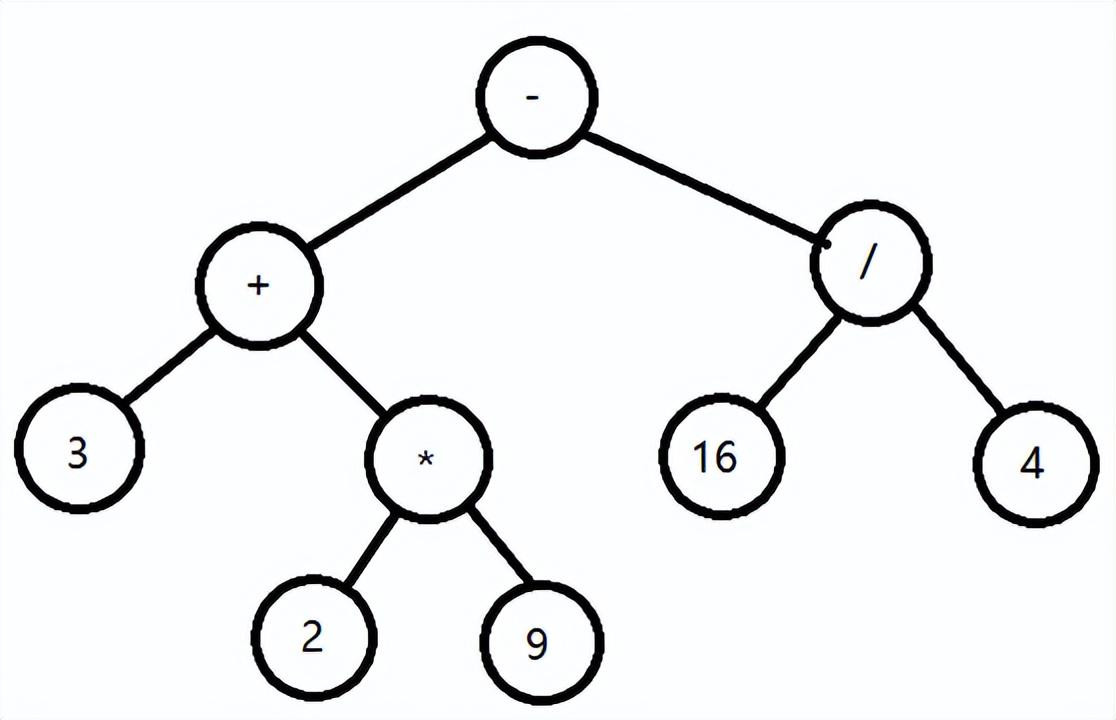
3. 转换过程
(1). 解析获取表达式的第一个字符3,因为表达式的树为空树,所以3是根节点。
(2). 获取第二个字符+,此时根结点为数字,将新结点作为根节点,原结点作为新结点的左孩子。
只有第二个会有这个可能,以后根节点肯定只为操作符。
(3). 获取第二个字符2,数字将沿着根结点插入到最右端。
(4). 获取第二个结点*,如果是操作符同根节点比较优先级,如果新结点的优先级高,则成为根结点的右孩子,原根结点的右孩子成为新结点的左子树。
(5). 获取第五个字符9,数字将沿着根节点直接插入到最右端。
(6). 获取第六个字符-,-与根结点+比较优先级,优先级相等,新结点成为根结点,原表达式成为新节点的左子树。
(7). 获取第七、八个字符组合为数字16,沿着根结点的右链直接插入到最右端。
(8). 获取第9个字符 / ,与根结点比较优先级,优先级高,成为根结点的右孩子,原根结点的右孩子成为左子树。
(9). 获取第10个字符4,数字沿根结点右链直接插入到最右端
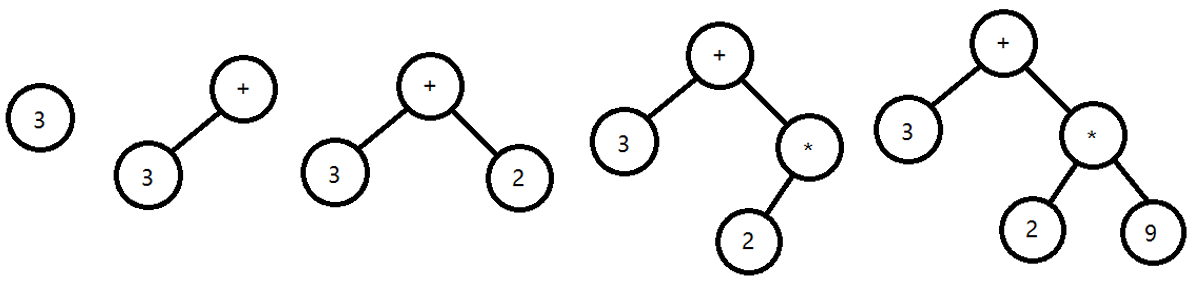

4. 总结
(1). 第一个节点先成为表示树的根
(2). 第二个结点插入时变为根,原根结点变为新结点的左孩子。
(3). 插入节点为数字时,沿根结点右链插入到最右端。
(4). 插入节点为操作符时,先与根结点操作符优先级对比。
a.优先级不高时,新结点成为根结点,原表达式成为新结点的左子树。
b.优先级高时,新结点成为根结点的右孩子,原根结点的右孩子成为新结点的左子树。
代码分享:
节点类:
/// <summary>
/// 树节点类
/// </summary>
public class Node
{
public Node Left { get; set; } //左孩子
public Node Right { get; set; } //右孩子
public int Data { get; set; } //数据
public bool IsOptr { get; } //是否为操作符
/// <summary>
/// 数据构造
/// </summary>
/// <param name="data"></param>
public Node(int data)
{
this.Data = data;
this.IsOptr = false;
}
/// <summary>
/// 操作符构造
/// </summary>
/// <param name="data"></param>
public Node(char data)
{
this.Data = data;
this.IsOptr = true;
}
public override string ToString()
{
if (IsOptr)
{
return Convert.ToString((char)Data);
}
else
{
return Data.ToString();
}
}
}二叉树实现类:
/// <summary>
/// 二叉树类处理四则运算
/// </summary>
public class BinaryTree
{
//成员变量
private Node _head; //头指针
private string expStr; //表达式字符串
private int pos = 0; //解析字符串当前位置
public BinaryTree(string constructStr)
{
this.expStr = constructStr;
CreateTree();
}
//创建表达式的树
public void CreateTree()
{
while (pos < expStr.Length)
{
Node node = GetNode();
if (_head == null)
{
//根节点不存在,第一个结点就为根
_head = node;
}
else if (!_head.IsOptr)
{
//若根节点为数字,当前节点为根,之前的根变为左孩子
node.Left = _head;
_head = node;
}
else if (!node.IsOptr)
{
//当前节点为数字
Node tempNode = _head;
while (tempNode.Right != null)
{
tempNode = tempNode.Right;
}
tempNode.Right = node;
}
else
{
if (GetPriority((char)node.Data) <= GetPriority((char)_head.Data))
{
//优先级不高时,新结点成为根结点,原表达式成为新结点的左子树
node.Left = _head;
_head = node;
}
else
{
//优先级高时,新结点成为根结点的右孩子,原根结点的右孩子成为新结点的左子树
node.Left = _head.Right;
_head.Right = node;
}
}
}
}
//创建节点
private Node GetNode()
{
char ch = expStr[pos]; //获取当前解析的字符
if (char.IsDigit(ch)) //判断当前字符是否为数字
{
//若操作的数字大于1位,需要用循环获取
StringBuilder numStr = new StringBuilder();
while (pos < expStr.Length && char.IsDigit(ch = expStr[pos]))
{
pos++;
numStr.Append(ch);
}
return new Node(Convert.ToInt32(numStr.ToString()));
}
else
{ //为操作符
pos++;
return new Node(ch);
}
}
//获取运算符的优先级,乘除优先级要高于加减
private int GetPriority(char optr)
{
if (optr == '+' || optr == '-')
{
return 1;
}
else if (optr == '*' || optr == '/')
{
return 2;
}
else
{
return 0;
}
}
private int PreOrderCalc(Node node)
{
int n1, n2;
if (node.IsOptr)
{
//先遍历计算表达式的结果
n1 = PreOrderCalc(node.Left);
n2 = PreOrderCalc(node.Right);
char optr = (char)node.Data;
switch (optr)
{
case '+':
node.Data = n1 + n2;
break;
case '-':
node.Data = n1 - n2;
break;
case '*':
node.Data = n1 * n2;
break;
case '/':
node.Data = n1 / n2;
break;
}
}
return node.Data ;
}
//获取四则运算的值
public int GetResult()
{
return PreOrderCalc(_head);
}
}测试
Console.WriteLine("-------------------二叉树处理四则运算-------------------------");
string expStr ="3+2*9-16/4";
//创建二叉树
BinaryTree bTree = new BinaryTree(expStr);
Console.WriteLine($"{expStr}结果为:{ bTree.GetResult()} ");
Console.ReadKey();运行结果:

原文链接:第十节:树与二叉树深度剖析(二) - Yaopengfei - 博客园