计算机图形学第3章圆的扫描转换-第三章结束

news2024/11/16 5:30:22

书用的是

书名:计算机图形学基础教程（VisualC++版）（第二版）

定价：44.5元

作者:孔令德

出版社：清华大学出版社

出版日期：2013-03-01

ISBN：9787302297529

习题3（续）

知识点

第3章圆的扫描转换

仅包含加减运算的顺时针绘制1/8圆的中点Bresenham算法原理，根据对称性可以绘制整圆。

提出问题：

默认的圆是圆心位于坐标系原点，半径为R的圆。
屏幕设备坐标系的原点位于左上角，绘制结果为1/4圆，需要进行圆心平移或使用自定义坐标系可以绘制整圆。
圆是椭圆的特例，使用椭圆中点Bresenham算法也可绘制。

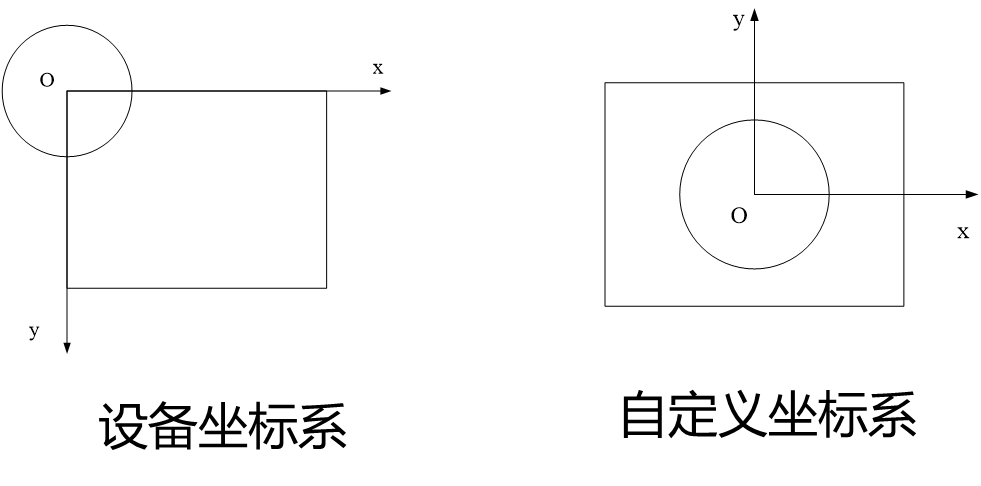
在这里插入图片描述

圆将平面划分成三个区域：对于圆上的点，F(x，y)＝0；对于圆外的点，F（x，y）＞0；对于圆内的点，F（x，y）＜0。

根据圆的对称性，可以用四条对称轴x＝0，y＝0，x＝y，x＝－y将圆分成8等份。
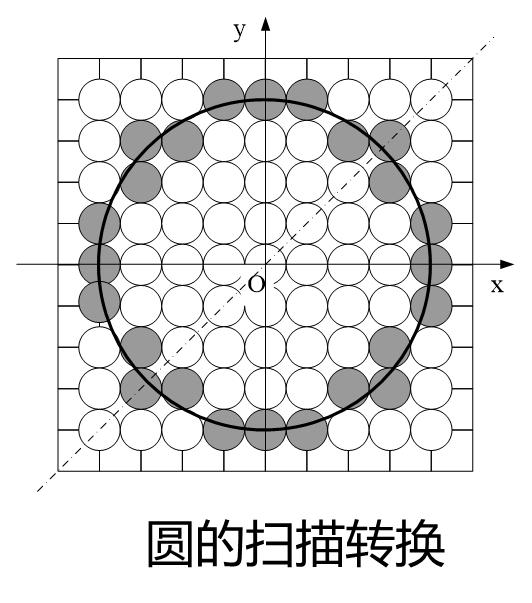
在这里插入图片描述

八分法画圆算法

只要绘制出第一象限内的1/8圆弧，根据对称性就可绘制出整圆。
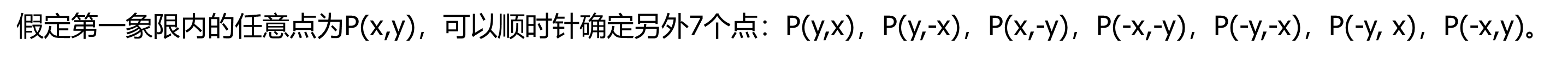
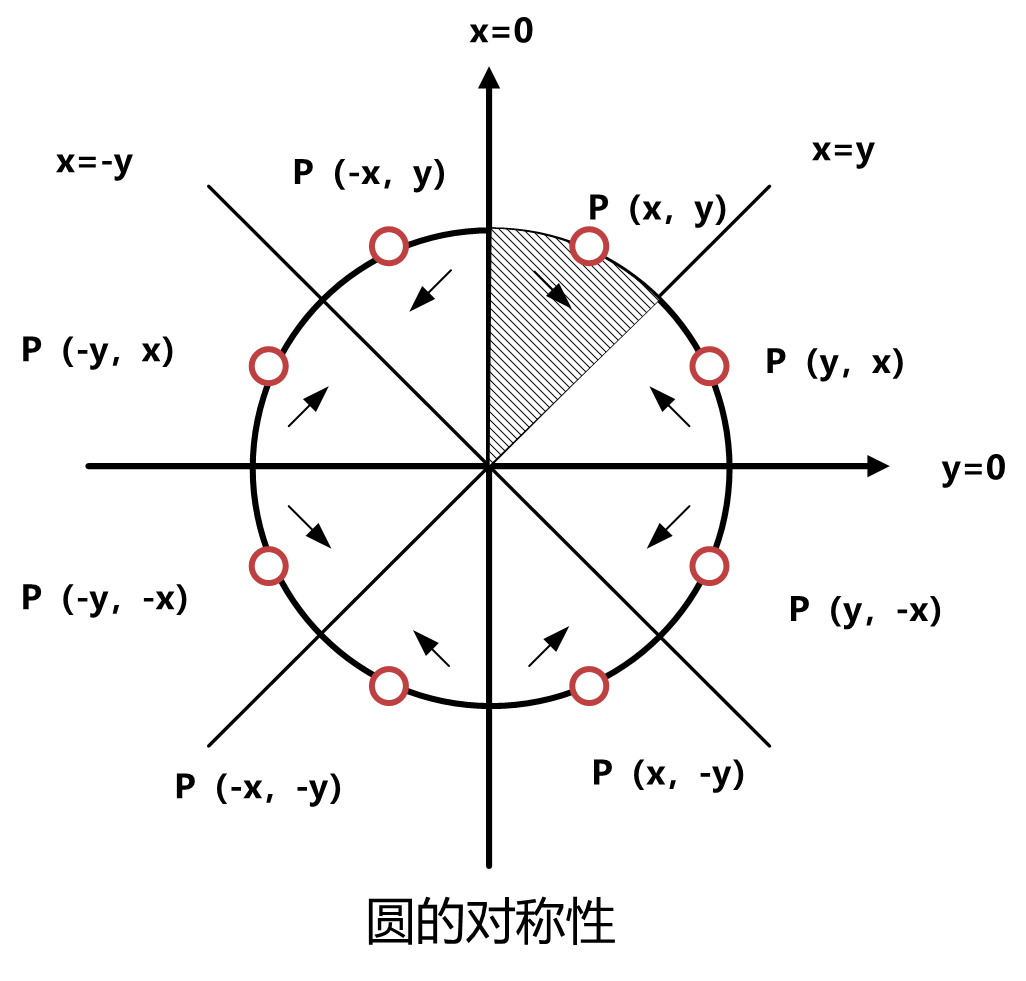
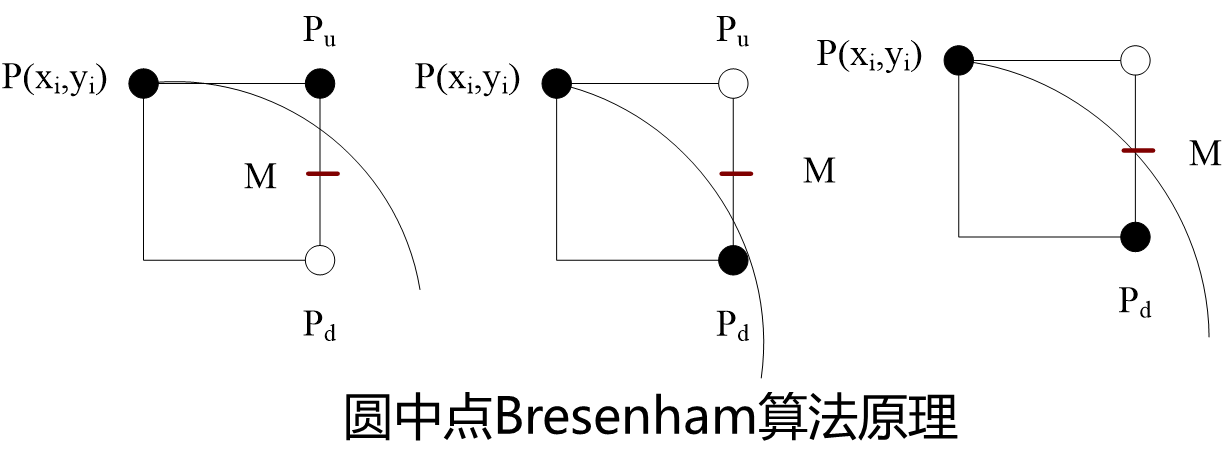
在这里插入图片描述

在这里插入图片描述

构造中点误差项

对应了上面三种弧的情况。

中点误差项的递推公式

分两种情况讨论
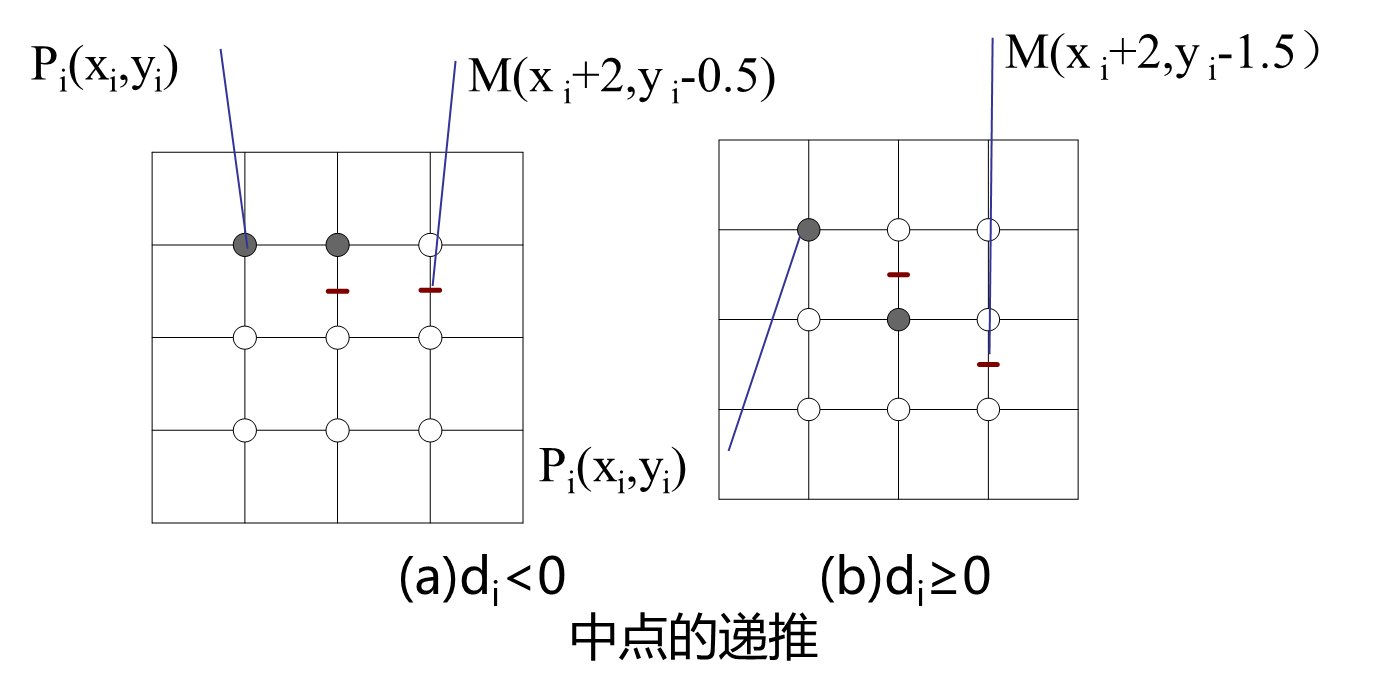
在这里插入图片描述

中点误差项的初始值

代码：

//圆中点Bresenham算法
void CTestView::MBCircle(double R,CDC *pDC )
{
	double x,y,d;	 
	d=1.25-R;x=0;y=R;
	for(x=0;x<=y;x++)
	{
		CirclePoint(x,y,pDC);//调用八分法画圆子函数
        if (d<0)
			d+=2*x+3;
        else
		{
			d+=2*(x-y)+5;
			y--;
		} 
     }
}

void CTestView::CirclePoint(double x, double y,CDC *pDC)//八分法画圆子函数
{
	 //圆心坐标
            CP2 pc=CP2((p0.x+p1.x)/2.0,(p0.y+p1.y)/2.0);        
	 //定义圆的边界颜色 
            COLORREF  clr=RGB(0,0,255);                         
	pDC->SetPixelV(Round(x+pc.x),Round(y+pc.y),clr); //x,y
	pDC->SetPixelV(Round(y+pc.x),Round(x+pc.y),clr); //y,x
	pDC->SetPixelV(Round(y+pc.x),Round(-x+pc.y),clr);//y,-x
	pDC->SetPixelV(Round(x+pc.x),Round(-y+pc.y),clr);//x,-y
	pDC->SetPixelV(Round(-x+pc.x),Round(-y+pc.y),clr);//-x,-y
	pDC->SetPixelV(Round(-y+pc.x),Round(-x+pc.y),clr);//-y,-x
	pDC->SetPixelV(Round(-y+pc.x),Round(x+pc.y),clr);//-y,x
	pDC->SetPixelV(Round(-x+pc.x),Round(y+pc.y),clr);//-x,y
}

CP2的定义在课本P95页。

椭圆的扫描转换

顺时针绘制1/4椭圆的中点Bresenham算法原理，根据对称性可以绘制完整椭圆。

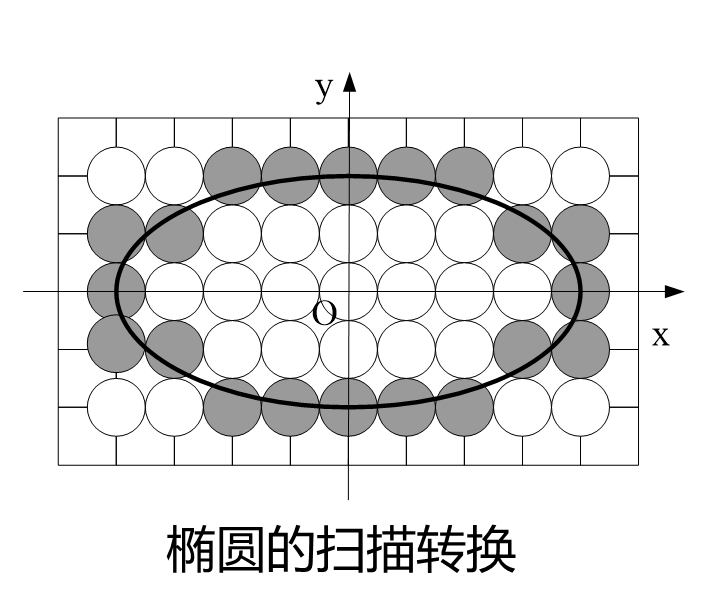
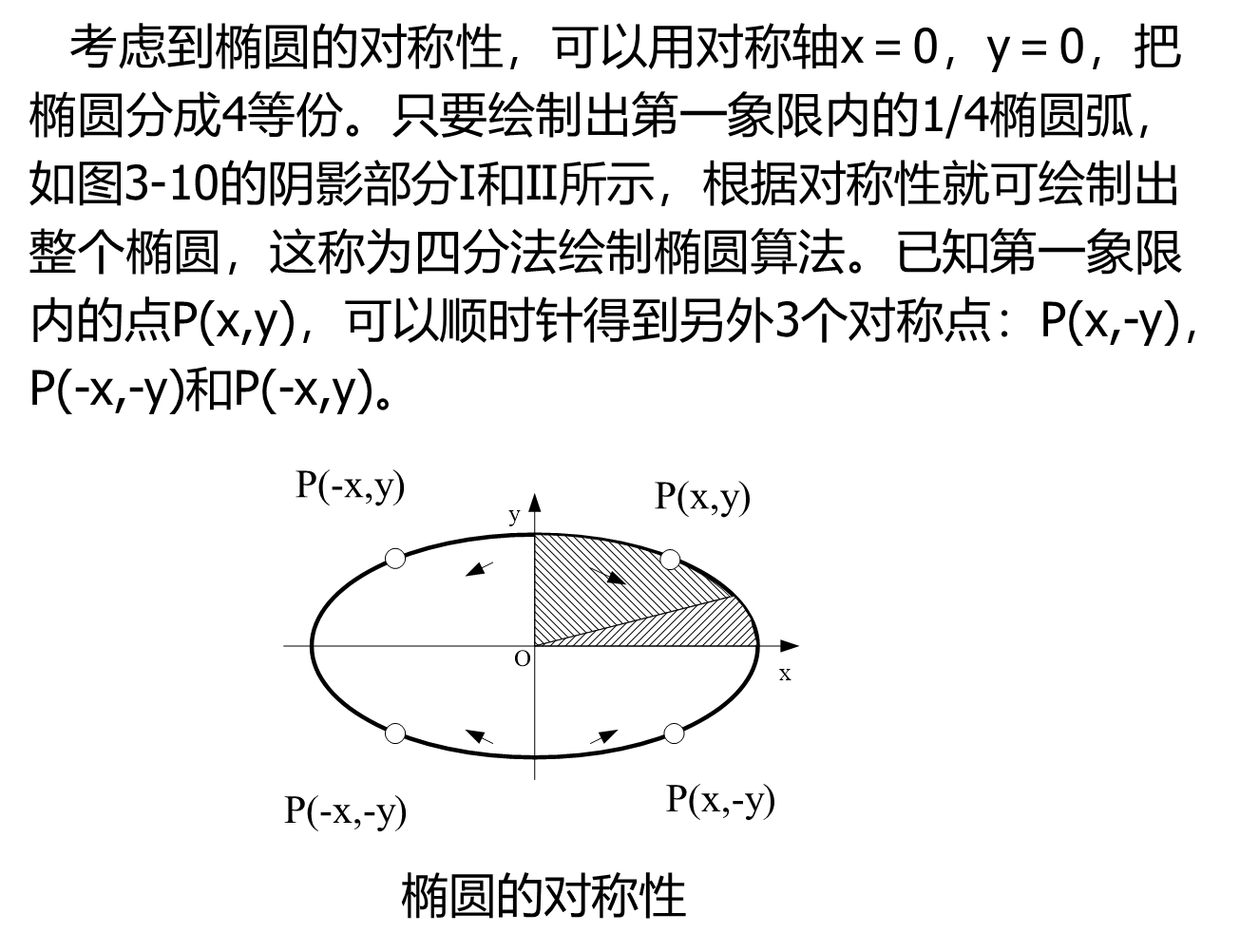
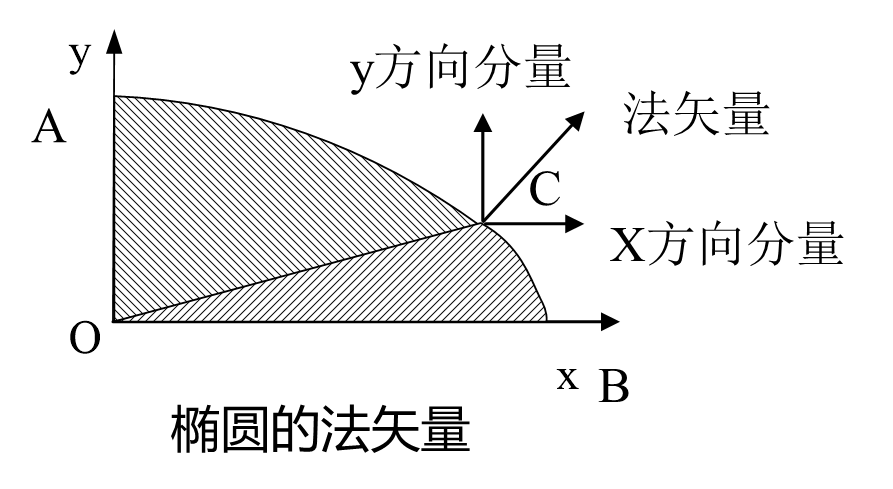
在这里插入图片描述

在这里插入图片描述

在部分Ⅰ椭圆的中点Bresenham的原理:每次在主位移x方向上走一步，y方向上退不退步取决于中点误差项的值。在部分Ⅱ：每次在主位移方向y上退一步，x方向上走不走步取决于中点误差项的值。

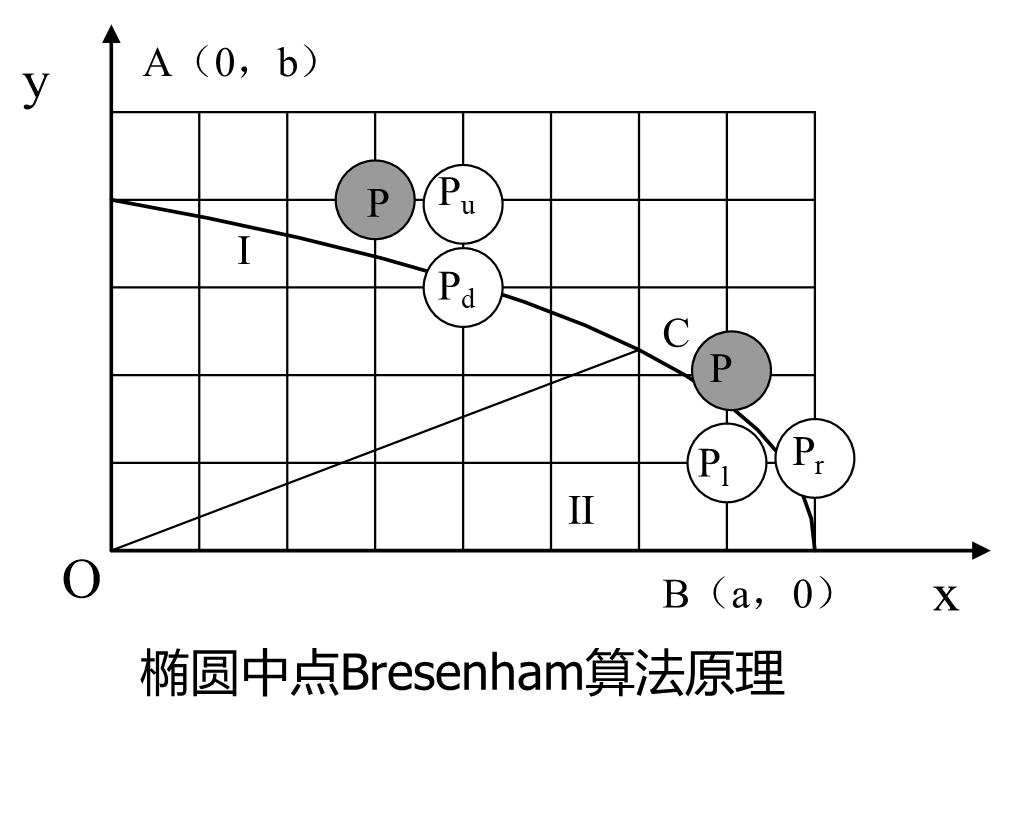
构造上半部分Ⅰ的中点误差项

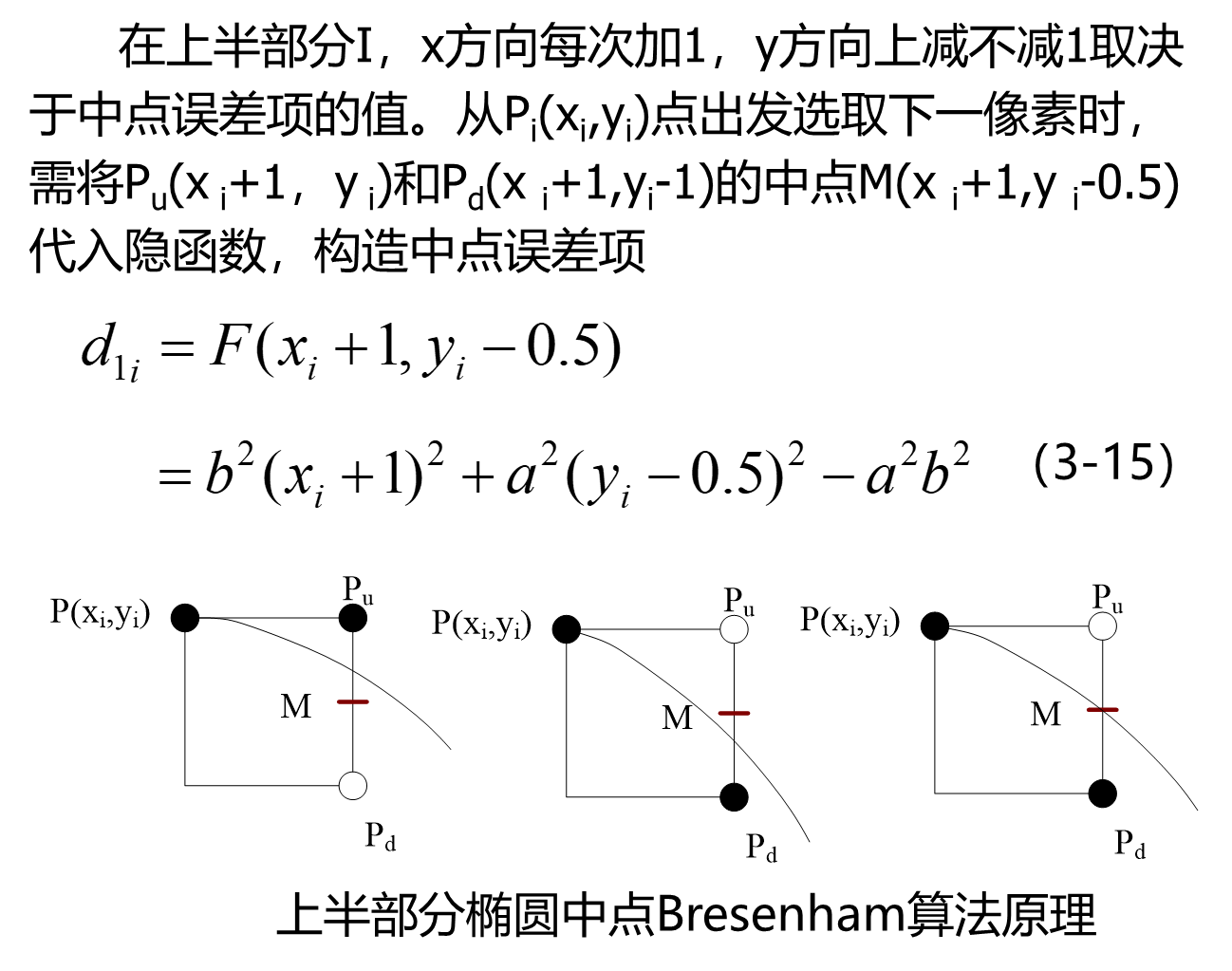
在这里插入图片描述

上半部分Ⅰ中点误差项的递推公式
分两种情况：
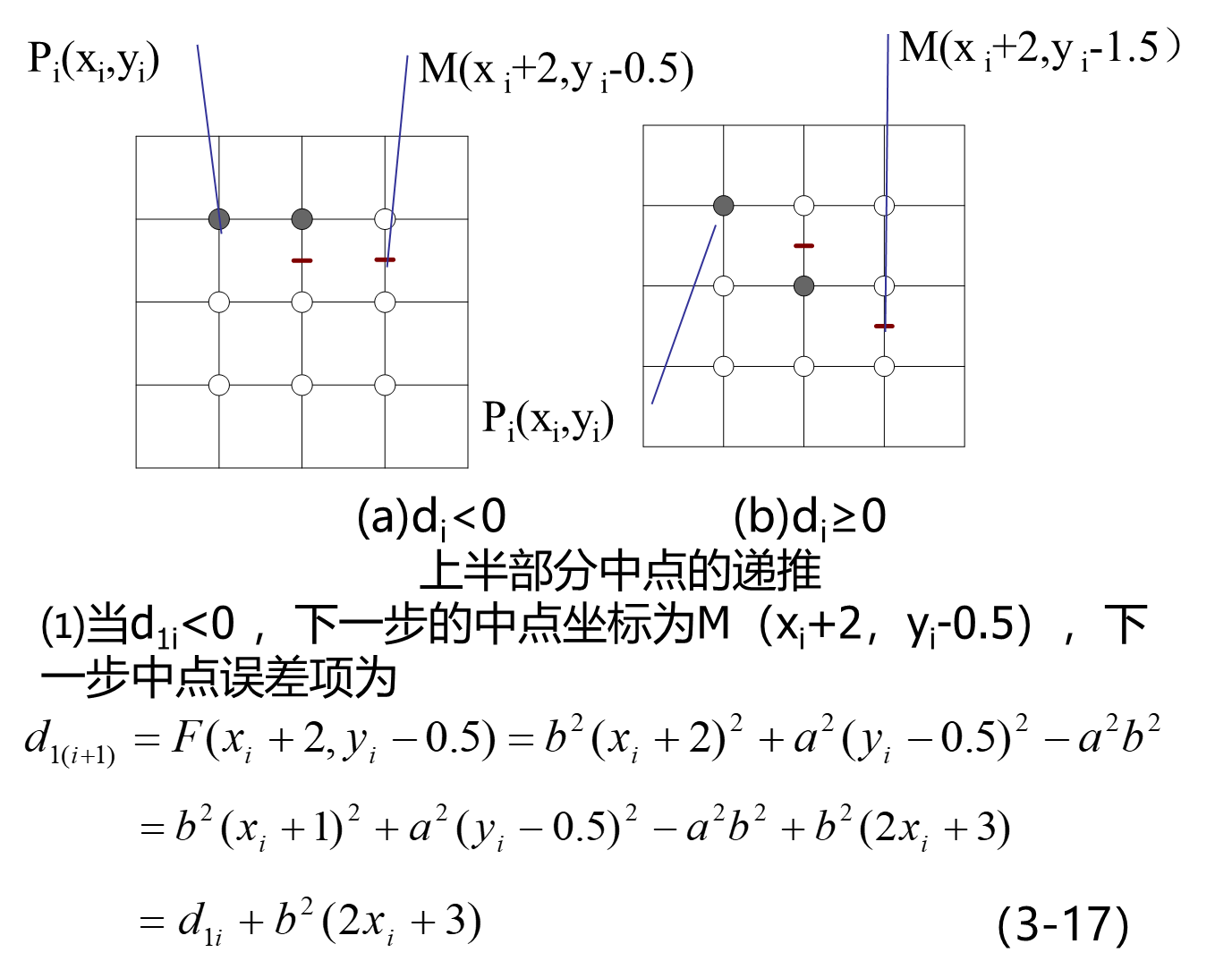
在这里插入图片描述

构造下半部分Ⅱ的中点误差项
在这里插入图片描述

在这里插入图片描述
下半部分Ⅱ的递推公式
现在如果考虑主位移方向再走一步，应该选择哪个中点代入中点误差项以决定应该选取的像素。分两种情况讨论。

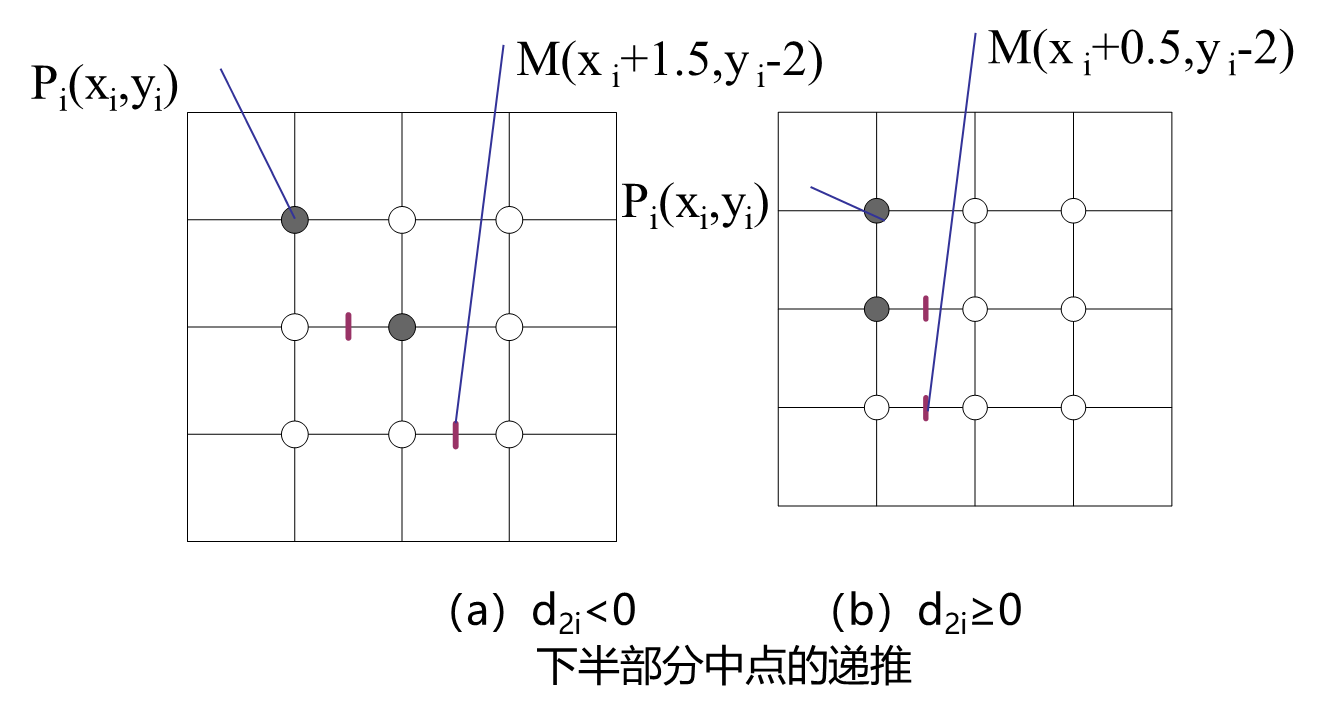
在这里插入图片描述
中点误差项的初始值

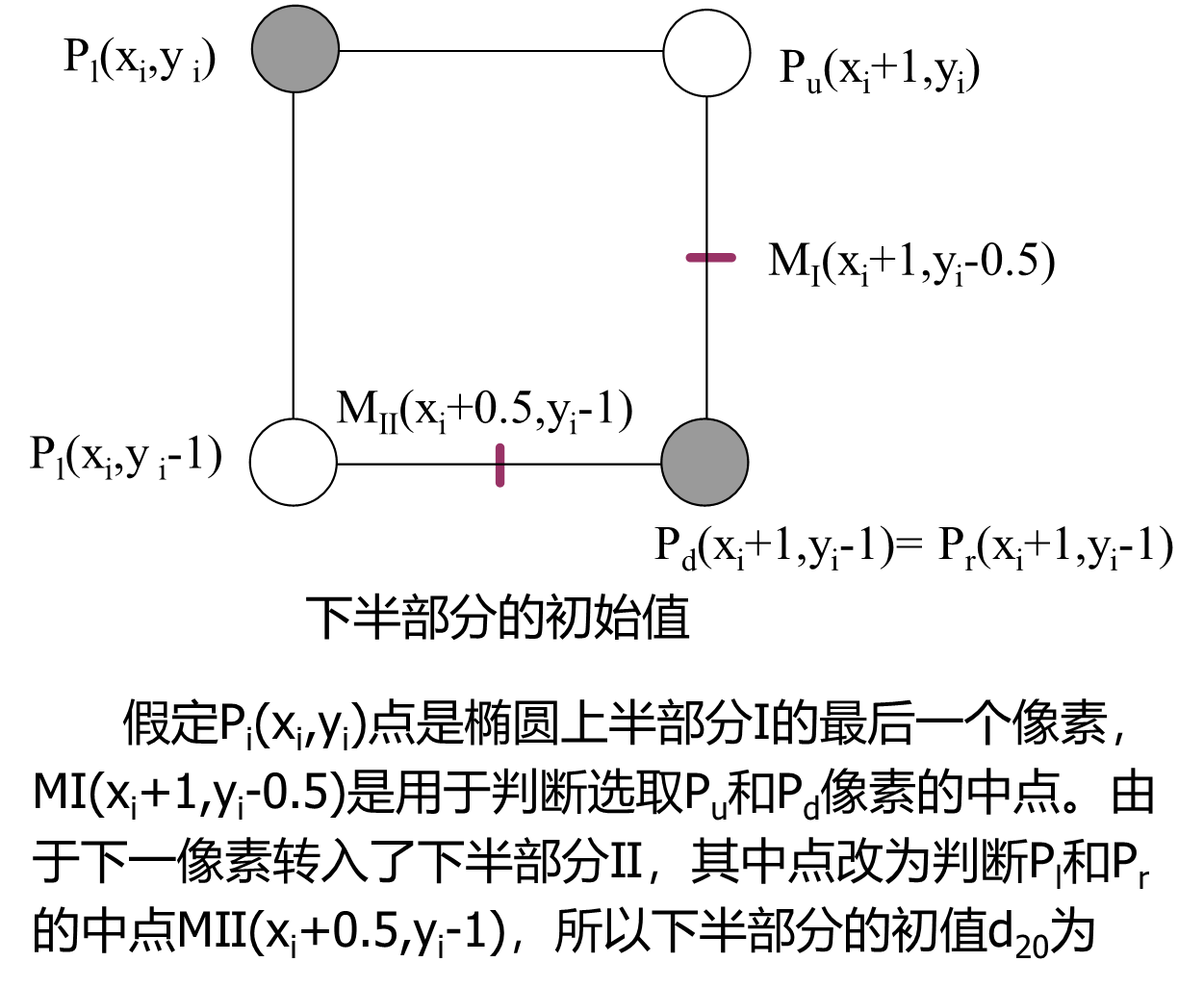
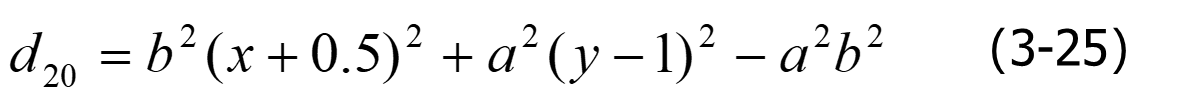
椭圆中点Bresenham算法

void CTestView::MBEllipse(CDC *pDC)//椭圆中点Bresenham算法
{
	double x,y,d1,d2,a,b;
	a=fabs(p1.x-p0.x)/2;
	b=fabs(p1.y-p0.y)/2;
	x=0;y=b;
	d1=b*b+a*a*(-b+0.25);
	EllipsePoint(x,y,pDC);
	while(b*b*(x+1)<a*a*(y-0.5))//椭圆AC弧段
	{
		if (d1<0)
		{
			d1+=b*b*(2*x+3);
		}
		else
		{
			d1+=b*b*(2*x+3)+a*a*(-2*y+2);
			y--;
		}
		x++;
		EllipsePoint(x,y,pDC);
	}
//椭圆CB弧段
	d2=b*b*(x+0.5)*(x+0.5)+a*a*(y-1)*(y-1)-a*a*b*b;
	while(y>0)
	{
		if (d2<0)
		{
			d2+=b*b*(2*x+2)+a*a*(-2*y+3);
			x++;
		}
		else
		{
			d2+=a*a*(-2*y+3);
		}
		y--;
		EllipsePoint(x,y,pDC);
	}
}

四分法画椭圆子函数

void CTestView::EllipsePoint(double x, double y,CDC *pDC)//四分法画椭圆子函数
{
	//椭圆中心坐标
           CP2 pc=CP2((p0.x+p1.x)/2.0,(p0.y+p1.y)/2.0); 	
           //定义椭圆的颜色
           COLORREF  clr=RGB(0,0,255); 
	pDC->SetPixelV(Round(x+pc.x),Round(y+pc.y),clr);
	pDC->SetPixelV(Round(-x+pc.x),Round(y+pc.y),clr);
	pDC->SetPixelV(Round(x+pc.x),Round(-y+pc.y),clr);
	pDC->SetPixelV(Round(-x+pc.x),Round(-y+pc.y),clr);
	pDC->MoveTo(Round(p0.x),Round(p0.y));
}

Wu反走样算法

算法原理

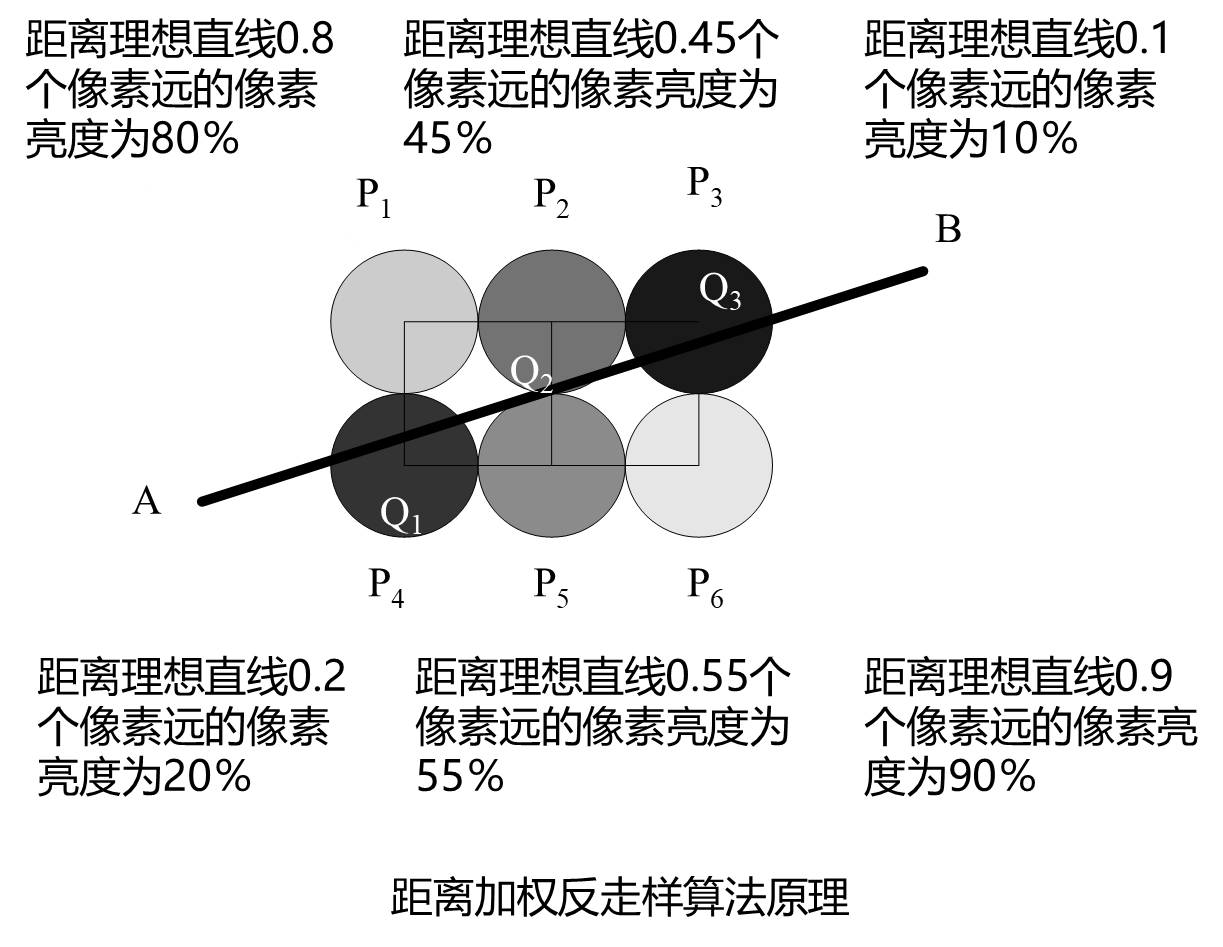
在这里插入图片描述
Wu反走样算法是采用空间混色原理来对走样进行修正。

空间混色原理指出，人眼对某一区域颜色的识别是取这个区域颜色的平均值。

在这里插入图片描述

代码

void CTestView::ALine(CDC *pDC)
{
	CPoint p0(-100,-50),p1(200,50),p;
	int dx,dy;
	dx=p1.x-p0.x;
	dy=p1.y-p0.y;
	double k=(double)dy/dx,e;
           for(p=p0,e=0;p.x<p1.x;p.x++)//不包括终点p1
	{
		pDC->SetPixelV(p.x, p.y,RGB(e*255,e*255,e*255));
                       pDC->SetPixelV(p.x, p.y+1,RGB((1-e)*255,
                                              (1-e)*255,(1-e)*255));	           
                       e+=k;
                       if(e>=1.0)
		{
	                    p.y++;
	                    e--;
		}				     
             }
}