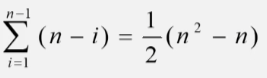文章目录

1. 冒泡排序
- 冒泡排序算法
- 冒泡排序算法分析
2. 快速排序
- 快速排序算法
- 快速排序算法分析

基本思想

每两个元素之间互相比较，如果发现大小关系相反，则将他们交换过来，直到所有记录都排好序为止。
假设希望是从小到大来排序，结果两个数的位置为 10、9，这时候就需要交换了。

常见的交换排序方法：

冒泡排序：O(n²)。
快速排序：O(nlog₂n)。

1. 冒泡排序

基本思想

每一趟将两两相邻的元素进行比较，小的放左边，大的放右边（交换数据），按照递增来排序，不满足条件就交换数据，满足则不管。

将某个数排到最终的位置，这一轮叫一趟冒泡排序。

每一趟冒泡排序可以让 1 个元素走到最终位置.
- 对于 6 个元素要进行 5 趟冒泡排序。
- n 个元素要进行 n-1 趟冒泡排序。

冒泡排序过程（升序）

初始：21，25，49，25*，16，08 ；n = 6。

第 2 趟
- 第 1 趟结束后：21，25，25*，16，08，49。
- 第 1 趟结束之后，49 已经有序了，那么下一趟就不用管它了。

第 2 趟
- 第 2 趟结束后：21，25，16，08，25*，49。
- 继续下一趟，每一趟增加一个有序元素。

第 3 趟结果：21，16，08，25，25*，49。
第 4 趟结果：16，08，21，25，25*，49。
第 5 趟结果：08，16，21，25，25*，49。

总结

n 个元素，总共需要 n-1 趟冒泡排序。
第 m 趟需要比较 n-m 次。
- 第 1 趟需要比较 5 次，第 2 趟 4 次，第 3 趟 3 次…… 。每一趟的排序的趟数 + 这趟的比较次数 = 元素个数 n 。

冒泡排序算法

//对顺序表L左冒泡排序
void bubble_sort(SqList &L)
{
		int m,i,j;
		RedType x;//交换临时存储

		for(m = 1;m <= n-1;m++)//总共需要m(n-1)趟冒泡排序
		{
				for(j = 1;j <= n-m;j++)//每一趟需要比较n-m次
				{
						if(L.r[j].key > L.r[j+1].key)//前面的比后面的大，发生逆序
						{
								x = L.r[j];
								L.r[j] = L.r[j+1];
								L.r[j+1] = x;
								//交换元素位置
						}
				}
		}
}

冒泡排序优点

优点：每趟结束时，不仅能挤出一个最大值到最后面位置，还能同时部分理顺其他元素；

如何提高效率？

一旦某一趟比较时不出现记录交换，则说明已经排好序了，就可以结束本算法来提高效率。

冒泡排序算法改进

当第 5 趟结束的时候，之前和之后的元素都已经有序了，所以后面的第 6、7 趟纯属于原地打转，浪费时间。

未发生交换时，后面几趟可以省略。

//对顺序表L进行改进的冒泡排序
void bubble_sort(SqList &L)
{
		int m,i,j;
		flag = 1;//flag作为是否有交换的标记
		RedType x;
	
		for(m = 1;m <= n-1 && flag == 1;m++)
		{
				flag = 0;
				for(j = 1;j <= m;j++)
				{
						if(L.r[j].key > L.r[j+1].key)//发生逆序
						{
								flag = 1;//发生交换，让flag为1，
								//若本趟没有发生交换，则flag保持为0，让最外层的for循环进不来
								
								x = L.r[j];
								L.r[j] = L.r[j+1];
								L.r[j+1] = x;
								//交换元素
						}
				}
		}
}

冒泡排序算法分析

时间复杂度

最好情况（正序）

比较次数：n-1 次。
移动次数：0次。

最坏情况（逆序）

比较次数：

移动次数：

冒泡排序的算法评价

冒泡排序最好时间复杂度是 O(n)。
冒泡排序最欢时间复杂度为 O(n²)。
冒泡排序平均时间复杂度为 O(n²)。
冒泡排序算法中增加一个辅助空间 temp，辅助空间为 S(n) = O(1)。
冒泡排序时稳定的（相同元素排好序后相对位置不变）。

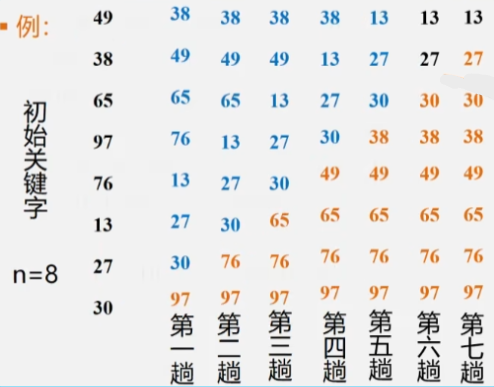
2. 快速排序

由冒跑排序改进的交换排序

基本思想

从需要排序的数据当中，任取一个元素（通常取第一个）为中心。
将所有比它小的元素一律往前放，比它大的元素一律往后放，形成左右两个子表；
接下来将左右两个子表用同样的方法进行排序（感觉和二叉排序树蛮像的），
直到每个子表的元素只剩一个。

举个例子

首先先选择第一个元素为中心点,然后划分左右子表。

子表也是用同样的方法排序，选择第一个为中心然后划分左右区。

当子表中只剩一个元素的时候，就不需要再划分了，说明已经排好位置了。

分析

基本思想：通过一趟排序，将待排序记录分割成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录进行排序，以达到整个序列有序。
具体实现：选定一个中间数作为参考，所有元素与之比较，小的调到其左边，大的调到其右边。
（枢轴）中间数：可以是第一个数、最后一个数、最中间一个数、任选一个数等。

算法步骤

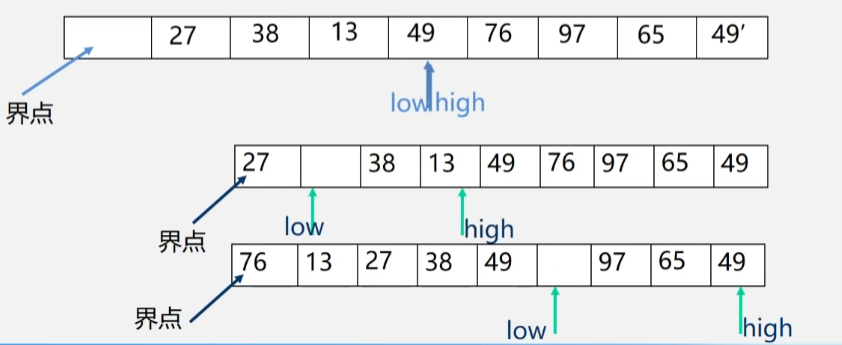
一趟快速排序的具体步骤如下：

选择待排序表中的第一个记录作为枢轴，将枢轴记录暂时存到 r[0] 的位置上。
- 另外设置两个指针 low 和 high ，初始时分别指向表的下界和上届（第一趟时，low = 1; high = L.length;）。
从表的最右测位置依次向左搜索，找到第一个关键字小于枢轴关键字 pivotkey 的记录，将其移动到 low 处。
- 具体操作：当 low < high 时，将 high 所指记录的关键字大于等于 pivotkey，则向左移动指针 high（执行操作 --high）；否则将 high 所指记录与枢轴记录交换。
然后再从表的最左侧位置，依次向右搜索找到第一个关键字大于 pivotkey 的记录和枢轴记录交换。
- 具体操作：当 low < high 时，若 low 所指记录的关键字小于等于 pivotkey，则向右移动指针 low（执行操作 ++low）；否则将 low 所指记录与枢轴记录交换。
重复步骤 2、3，直到 low 与 high 相等为止。
- 此时 low 和 high 的位置即为枢轴在此趟排序中的最终位置，原表被分为两个子表。

快速排序特点

每一趟的子表的形成是采用从两头向中间交替式逼近法；
- 一开始将枢轴元素放在 0 号位置，那么它的位置就空出来了，从后面挑比它小的元素填进来，此时小元素的原来位置就空了，再从前面般比这个移动过去的小的元素大的元素填过去，前挑大后填，后挑小前填，依次类推。
- 直到 low 和 high 重合了，这个地方就是俺们放中心点的位置。
由于每趟中对各子表的操作都相似，可采用递归算法。

快速排序算法

//对顺序表L左快速排序
void Quick(SqList &L)
{
		Qsort(L,1,L.length);
}

//调用前置初值：low=1;high=L.length
//对顺序L中的子序列L.r[low...high]左快速排序
void Qsort(SqList %L,int low,int high)
{		
		if(low < high) //长度大于1
		{
				pivotloc = partition(L,low,high);
				//将L.r[low...high]一分为二，pivotloc为枢轴元素排好序的位置

				QSort(L,low,pivotloc-1);//对左子表递归排序
				Qsort(L,pivotloc+1,high);//对右子表递归排序
		}
}

//对顺序表L中的子表r[low...high]进行一趟排序，返回中心点位置
int Partition(SqList &L,int low,int high)
{
		L.r[0] = L,r[low];	//用子表中的第一个记录左枢轴记录
		pivotkey = L.r[low].key;	//枢轴记录关键字保存在pivotkey中

		while(low < high)	//从表的两段交替的向中间扫描
		{
				while(low<high && L.r[high].key >= pivotkey)
				{
						--high;
				}
				L.r[low] = L.r[high];	//将比中心点小的元素移到到低端
				
				while(low<high && L.r[low].key <= pivotkey)
				{
						++low;
				}
				L.r[high] = L.r[low];	//将比中心点大的元素移动到高端
		}		

		L.r[low] = L.r[0];	//找到了中心点该存放的位置了，将它存进去
		return low;		//返回中心点存储的位置
}