一、本周周赛总结

• T3又被脑筋急转弯卡了，想了一小时Dp。
• T1 脑筋急转弯+数学。
• T2 脑筋急转弯+快速幂取模。
• T3 脑筋急转弯+排序。
• T4 枚举计算/DP。
  

二、 [Easy] 6337. 统计桌面上的不同数字

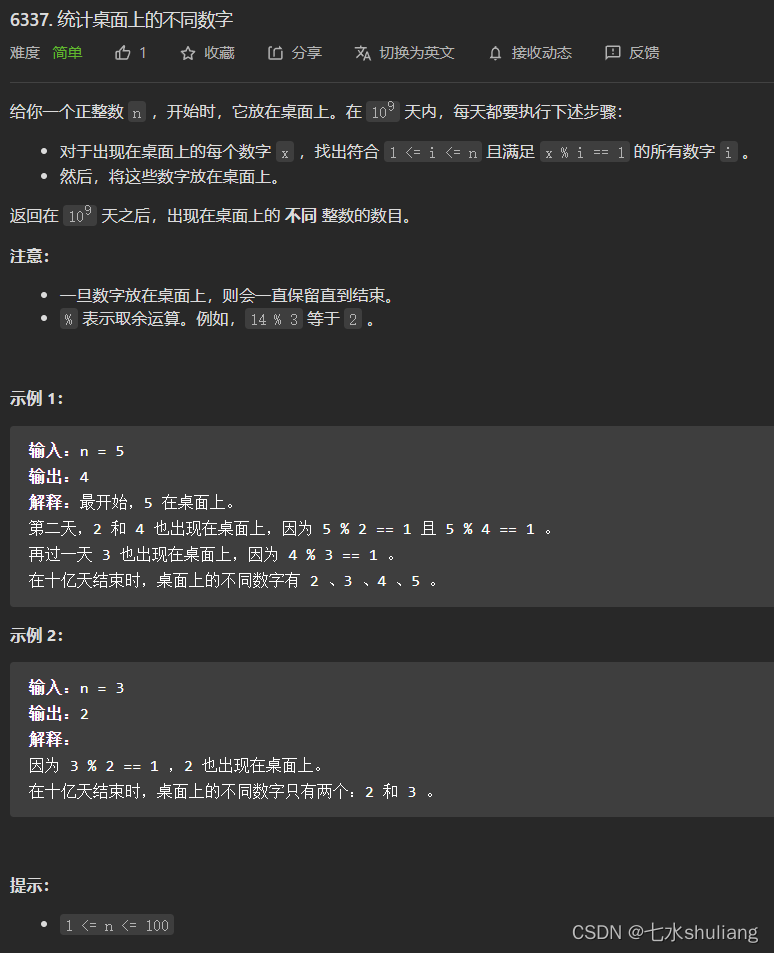
链接: 6337. 统计桌面上的不同数字

1. 题目描述

2. 思路分析

• 每次操作，每个数的i-1都会新增出来。但1不会。
• 也就是最终2~n之间的数都会出来。
• 题目限制n<=100,但 进行1e9次操作，因此必能操作到头。
• 也就是除了n=1的情况，其它都会出现2~n，即n-1个数。

3. 代码实现

class Solution:
    def distinctIntegers(self, n: int) -> int:
        if n == 1:
            return 1
        return n-1

三、[Medium] 6338. 猴子碰撞的方法数

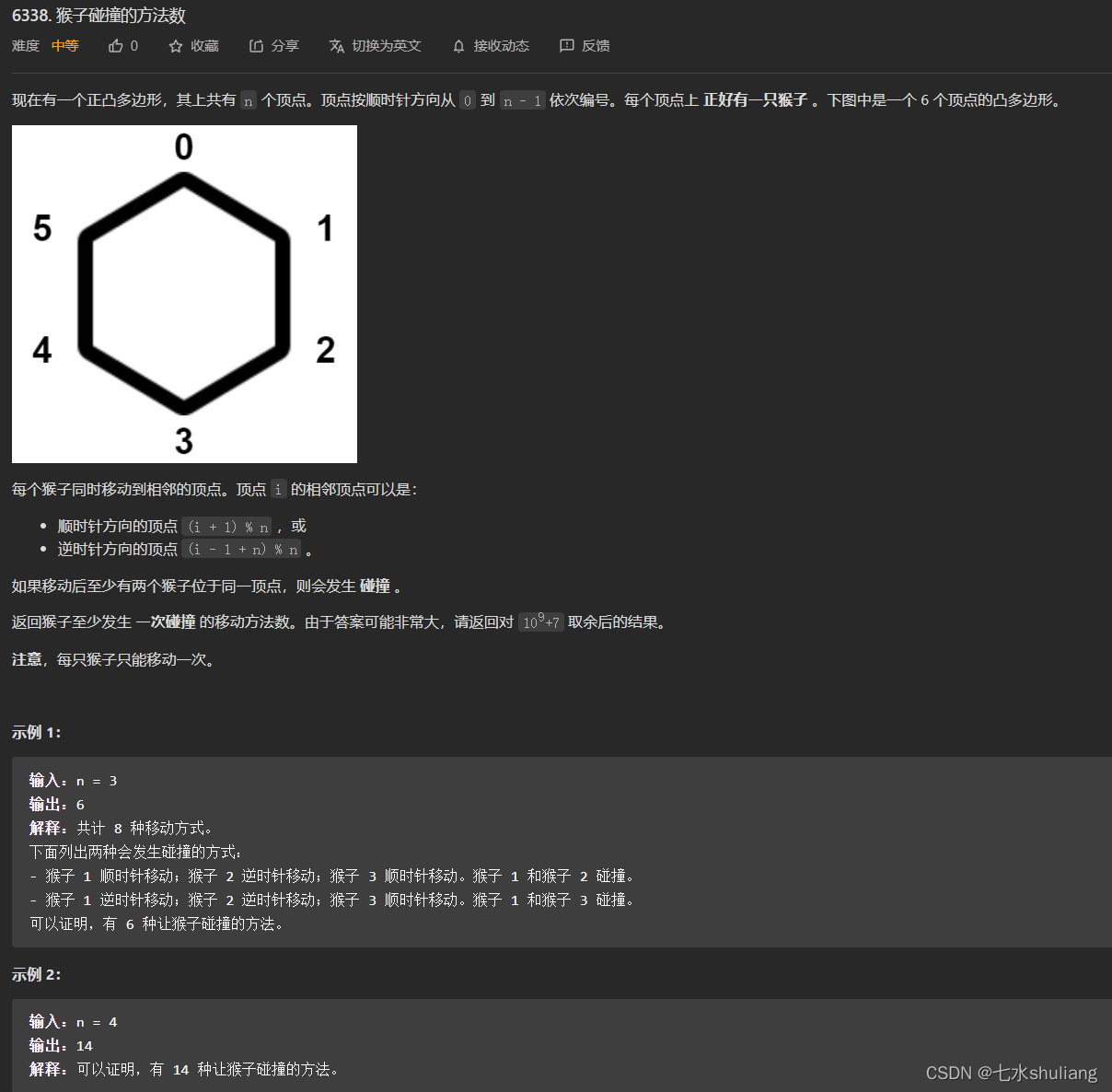
链接: 6338. 猴子碰撞的方法数

1. 题目描述

2. 思路分析

题目有歧义。实际上路径也不能相撞，否则偶数的话可以相邻猴子两两交换位置。

• 考虑不撞的方法，只有两种，就是一起顺时针或逆时针走。
• 所有走法一共有2**n。需要用快速幂取模模板。
• 这里是py就逃课了。

---

• 一开始太相信py的大数，直接2**n-2，再取模，确实TLE，pow就没问题。

3. 代码实现

MOD = 10**9+7
class Solution:
    def monkeyMove(self, n: int) -> int:
        return (pow(2,n,MOD) - 2) % MOD 

四、[Hard] 6339. 将珠子放入背包中

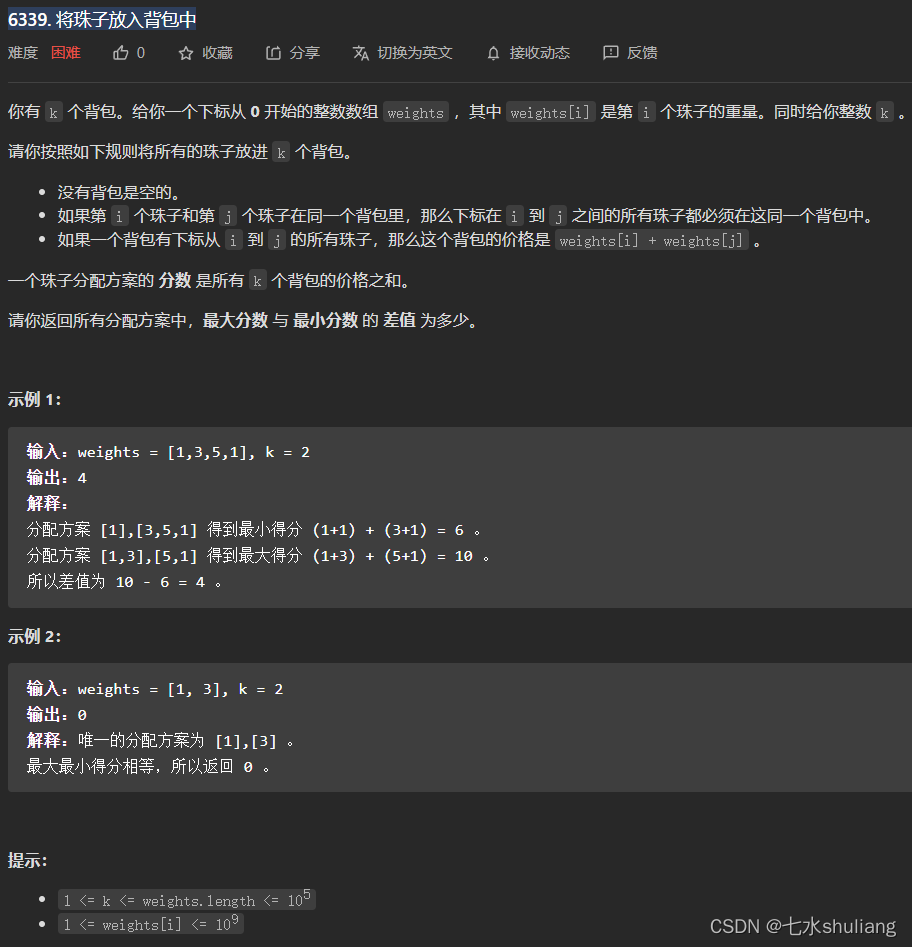
链接: 6339. 将珠子放入背包中

1. 题目描述

2. 思路分析

这题看似能DP，于是优化了一个小时都没做出来。
转化下思路就过了。

• 在最大最小值里，首尾两个数必会出现1次，因此无视。
• 那么剩下的从哪取呢，想想有k-1根棍子分割这n个柱子。
• 柱子两边的数就是这根棍子的贡献。那么排序所有可能的贡献，最大的k-1个和最小的k-1个就是答案。

3. 代码实现

class Solution:
    def putMarbles(self, w: List[int], k: int) -> int:
        if k == 1 or k == len(w):
            return 0
        a = []
        for x,y in pairwise(w):
            a.append(x+y)
        a.sort()
        return sum(a[-k+1:]) - sum(a[:k-1])

五、[Hard] 6340. 统计上升四元组

链接: 6340. 统计上升四元组

1. 题目描述

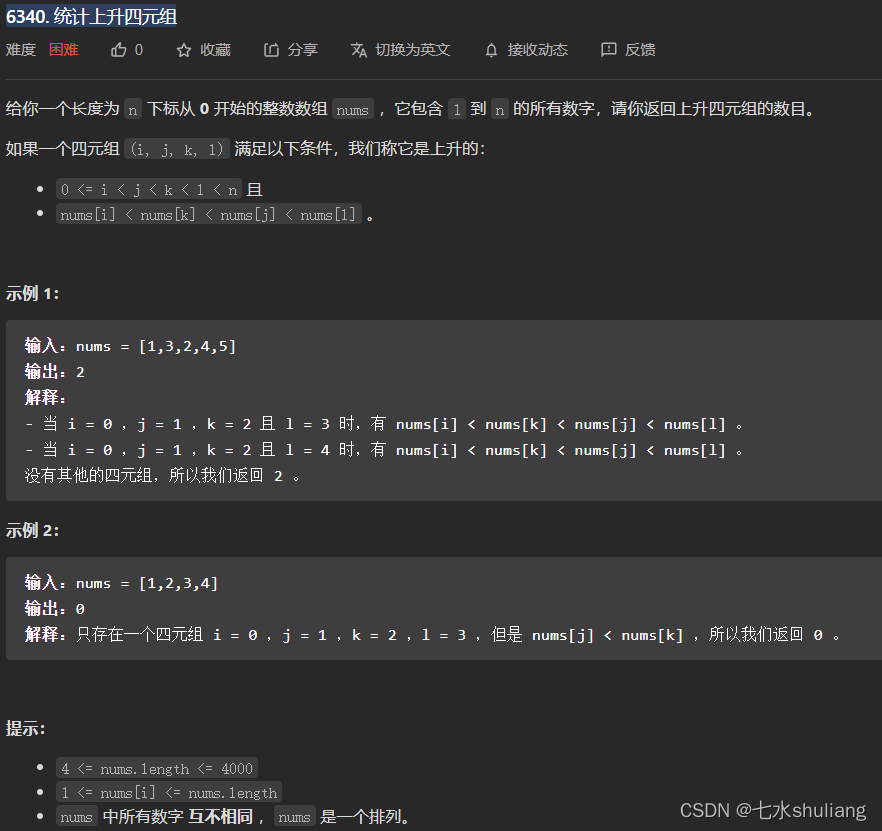
2. 思路分析

注意题目要求里k和j的相对位置，要求a1<a3<a2。

• 两层循环枚举j和l。即第二个数和第四个数。
• 在j和l之间的数k，如果小于nums[j]，则可以去j前边找有多少个i满足nums[i]小于num[k]，那就是几个ik对；如果大于，则可以加上所有k的贡献（即有多少ik对）。
• 因此用一个有序集合pre跟着j走，记录j之前所有数，便于二分。
• 外层循环枚举j，内层循环可以看成两种：
  • j右侧的数大于nums[j]的是l，小于的是k。
  • 即同时枚举k和l。
• 这里用的nnlgn的做法，后续补充一个n*n的dp。

---

• 补充n方做法。
• 枚举j和k，这样当nums[j]>nums[k]时，k后边能选大于nums[j]的数，j前边能选小于nums[k]的数。
• 如果能计数，则乘起来即可。
• 可以用n方的时间计算这两个二维数组:
  • great[i][v]代表i右边大于v的数有多少个。
  • less[i][v]代表i左边小于v的数有多少个。
• 具体计算方法有点类似子序列自动机，从前一个状态整体迁移过来，然后再计算本身的差异。
• 注：我后来试了树状数组，发现nnlgn的树状数组做法和n方的dp时间表现没什么差异：py的空间大了确实费性能。

---

• 补充一个方法三，空间O(n)，时间O(n²)，注释写的很详细。表现良好1276ms.

3. 代码实现

class Solution:
    def countQuadruplets(self, nums: List[int]) -> int:
        n = len(nums)
        ans = 0
        from sortedcontainers import SortedList
        pre = SortedList()
        for j in range(n):
            mid = 0
            for l in range(j+1,n):
                if nums[l] < nums[j]:
                    mid += pre.bisect_left(nums[l])
                else:
                    ans += mid
            
            pre.add(nums[j])
        return ans       

n方dp

class Solution:
    def countQuadruplets(self, nums: List[int]) -> int:
        n = len(nums)
        great = [[]] * n 
        great[-1] = [0]*(n+1)
        for k in range(n-2,-1,-1):
            great[k] = great[k+1][:]
            for v in range(1,nums[k+1]):
                great[k][v] += 1
        ans = 0
        less = [0]*(n+1)
        for j in range(1,n-1):
            for v in range(nums[j-1],n+1):
                less[v] += 1
            for k in range(j+1,n-1):
                if nums[j] > nums[k]:
                    ans += less[nums[k]] * great[k][nums[j]]
        return ans

方法三

class Solution:
    def countQuadruplets(self, nums: List[int]) -> int:
        n = len(nums)
        ans = 0 
        cnt = [0] * n   # cnt[j]表示以j为高点的，132形状的三元组数量
        for l in range(n):
            small = 0  # j前边小于nums[l]的数量
            for j in range(l):
                if nums[j] < nums[l]:  # 如果高点小，就是满足
                    ans += cnt[j]
                    small += 1  # 且记一个小的数
                else:
                    cnt[j] += small  # 否则可以贡献small个三元组
        return ans 

六、参考链接