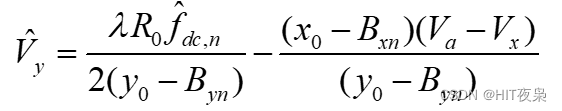二分查找算法的时间复杂度是O(logN) ，更优于传统的遍历数组算法值得我们学习。

注意二分查找一般使用的前提是：待操作的数组的元素有某种规律也就是要有二阶性，二阶性就是在数组中选取一点根据该数组元素某种规律可以把数组分为两部分，可以舍弃一部分然后在剩下的部分找出结果。

简单二分查找算法

解法一：遍历数组，时间复杂度O(n)。

解法二：二分查找，时间复杂度O(logN)。

该题数组元素是升序，因此该数组具有二阶性。可以使用二分查找算法。

二分查找得到target下标的情况  ：

1.取middle时直接取到target  

2.当left == right时，可能会取到target的下标     left == right是找到target的最后机会，如果a[left] != target则查找失败。

class Solution {
public:
	int search(vector<int>& nums, int target) {
		int left = 0, right = nums.size() - 1;
		while (left <= right)
		{
			int mid = left + (right - left) / 2;//防止数据溢出
			if (nums[mid] < target)
				left = mid + 1;
			else if (nums[mid] > target)
				right = mid - 1;
			else
				return mid;
		}
		return -1;
	}
};

进阶二分查找算法

该数组的元素是非递减序的，也就是说元素是以增大或不变的顺序排序的，因此待操作数组具有二阶性。

目标值的开始位置和结束位置要分开来找。

求目标值的开始位置：

选取mid（二分查找过程中选取的中点下标）：mid = left + (right - left) / 2

二分查找循环条件：left < right

求目标值的结束位置：

mid = left + (right - left + 1) / 2

二分查找循环条件：left < right

class Solution {
public:
	vector<int> searchRange(vector<int>& nums, int target) 
	{
		//处理数组元素为0的情况
		if (0 == nums.size())
			return { -1,-1 };
		int begin = 0;
		//1.求目标值的开始位置
		int left = 0, right = nums.size() - 1;
		while (left < right)
		{
			int mid = left + (right - left) / 2;
			if (nums[mid < target])
				left = mid - 1;
			else
				right = mid;
		}
		//判断是否有结果
		if (nums[left] != target)
			return { -1,-1 };
		else begin = left;
		//2.求目标值的结束位置
		left = 0, right = nums.size() - 1;
		while (left < right)
		{
			int mid = left + (right - left + 1) / 2;
			if (nums[mid] <= target)
				left = mid;
			else
				right = mid - 1;
		}
		return { begin,right };
	}
};