目录
一、实验目的
二、问题描述
三、实验要求
四、实验内容
动态规划法
算法描述
算法伪代码描述
算法复杂度分析
数据测试
二分优化的动态规划法
算法描述
二分优化:
算法伪代码
算法复杂度分析
数据测试
单调决策优化的动态规划法
算法描述
算法伪代码描述
算法复杂度分析
数据测试
空间降维优化
算法分析
算法伪代码描述
数据测试
综合分析
五、实验结论
一、实验目的
1. 掌握动态规划算法设计思想。
2. 掌握扔鸡蛋问题的动态规划法。
二、问题描述
扔鸡蛋问题是计算机程序设计中的一个经典问题。从一幢楼房的不同楼层往下扔鸡蛋,用最少的最坏情况试验次数,确定鸡蛋不会摔碎的最高安全楼层。仅有一个鸡蛋供试验时,只能采用顺序查找法。有足够多的鸡蛋时,可以采用二分查找法。有多于一个但数量有限的鸡蛋时,采用动态规划方法求解。双蛋问题(two-egg problem)是本问题的一个特例,曾出现于谷歌的程序员面试题中。
有一幢楼房高层。某人准备了N个鸡蛋供试验。他想知道鸡蛋从几层扔下不会摔碎,并确定出最高安全楼层。试验过程中,鸡蛋没有摔碎则可以继续使用,摔碎了则需要换一个鸡蛋继续试验。为保证试验成功,此人要设计一个程序,以最小化最坏情况的试验次数F(M, N)。作为一个数学抽象,本问题采用一些理想化假设:所有鸡蛋抗摔能力相同,不计重复坠地的累积损伤,且忽略试验结果的偶然性。试验成功的标准是在N个鸡蛋用完之前,精确确定最高安全楼层是哪一层。允许有鸡蛋剩余。
如果只有N=1个鸡蛋供试验,则为了保证试验成功,只能从一层开始逐层往上试验。这相当于采用顺序查找算法,最坏试验次数F(M, 1)=M。如果一层就碎了,则最高安全楼层为0。如果M层还不碎,则最高安全楼层为M。
三、实验要求
1. 给出解决问题的动态规划方程;
2. 理论分析该算法的时间复杂度;
3. 分别测试M=10000, 20000, …, 100000, N=20时以及M=50000, N=11, 12, …, 20时的算法运行时间,并分析实验结果;
4. 依次在终端输出M=10000, N=1~20时的F(M, N)值,实验课时检查该代码,限用C或C++语言编写。
四、实验内容
动态规划法
算法描述
动态规划的优势在于对于每一个子问题都只求解一次,而后将该结果保存,但再次对
子问题的求解时直接使用即可,这样子避免了许多子问题被重复计算多次,造成的时间复杂度较高,耗时较长的问题。
因此,我对状态进行了如下定义:
dpi,j 表示用i个鸡蛋可以确认j层楼的门槛层的最少操作次数
在状态定义完成后,便要考虑动态规划的另一个条件,初始态,即边界条件,从题目描述中我们可以得知,当鸡蛋数i=1时,对于j层楼我们需要从第一层楼开始向上测试,所需要的最少操作数目为dp1,j =j,当楼层数j=0时,对于i个鸡蛋,我们需要的最少操作次数为dpi,0 =0。
对于每一个状态,对其考虑状态转移:
对于i个鸡蛋𝑗层楼,在第𝑥层(1 ≤ 𝑥 ≤ 𝑗)扔鸡蛋时,我们用𝑝𝑥表示确定门槛层需要的操作次数。对于每个鸡蛋:
• 若鸡蛋破碎,子问题的规模是鸡蛋数变为i - 1,楼层数变为𝑥 - 1层,其最优解为dpi-1,x-1 ,最后再加上本次的操作次数,所以操作次数 𝑝𝑥 =dpi-1,x-1 + 1;
• 若鸡蛋没有破碎,此时子问题的规模是鸡蛋数不变,楼层数变为𝑗 - 𝑥层,其最优解为𝑑𝑝𝑖,𝑗-𝑥,最后再加上本次的操作次数,所以操作次数 𝑝𝑥 = dpi,j-x + 1。
但由于我们并不知道扔下去的鸡蛋是否会碎,因此我们要在两种情况的查找次数中选择最大值,即考虑最坏的情况,所以𝑝𝑥 = max(dpi-1,x-1 , dpi,j-x ) + 1
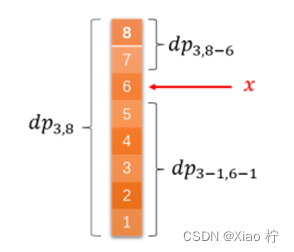
综上分析,可以写出动态规划方程:
dpi,j = { p1 , p2 ,p3 ,……., pj }
即 dpi,j=min{max(dpi-1,x-1, dpi,j-x) + 1} 1<=x<=j
其中,边界条件为dp1,j =j,dpi,0 =0
动态规划的过程实际上就是一个填表的过程,以下为模拟填表的过程:当我们要填𝑑𝑝4,6的时候,根据动态规划方程,我们需要枚举每一个扔鸡蛋的楼层𝑥(1 ≤ 𝑥 ≤ 6)作为我们的上一个状态,所有的状态中选择最小的答案即为我们的答案。

算法伪代码描述
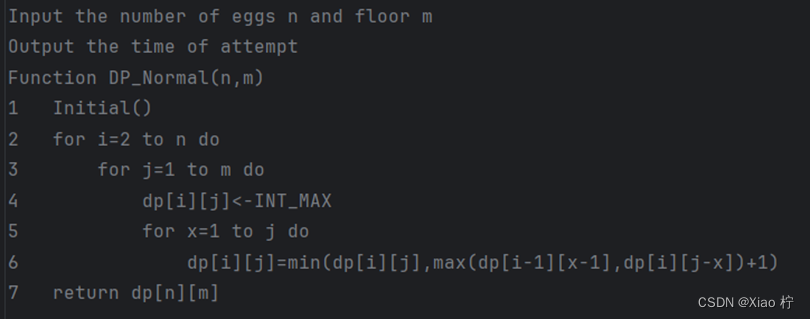
算法复杂度分析
对于n个鸡蛋和m层楼的跌落实验:
时间复杂度:状态数量一共为n*m个,并且对于每个状态枚举扔鸡蛋的楼层需要O(m)的时间,一共为O(nm2)
空间复杂度:由于所有的状态需要 O(1)的空间存储,所以空间复杂度为𝑂(nm)
数据测试
为降低偶然性,我们对每组数据重复测试 10 次再取平均值,并利用公式T=T0*n*m2n0*m0^2 绘制理论运行时间曲线。
当M=10000, 20000, …, 100000, N=20时
| 楼层 m | 10000 | 20000 | 30000 | 40000 | 50000 | 60000 | 70000 | 80000 | 90000 | 100000 |
| 操作数 | 14 | 15 | 15 | 16 | 16 | 16 | 17 | 17 | 17 | 17 |
| 实际耗时s | 13.5 | 54.3 | 122.6 | 210.9 | 329.2 | 472.3 | 642.5 | 839.4 | 1072.1 | 1320.7 |
| 理论耗时s | 13.5 | 54.0 | 121.5 | 216.0 | 337.5 | 486.0 | 662.5 | 864.0 | 1093.5 | 1350 |

由上图所示,蓝色曲线为动态规划法实际运行时间拟合曲线,橙色曲线为动态规划法理论运行时间拟合曲线,两条曲线基本吻合,故动态规划法的时间复杂度满足𝑂(nm2)。
当M=50000, N=11, 12, …, 20,程序无法在可接受的时间内求出答案
由于最基本的动态规划方程,其时间复杂度仍达到了n^3级,在面对大规模数据时,需要较长的时间才能计算出来,因此算法优化就十分重要
二分优化的动态规划法
算法描述
对于动态规划方程:
dpi,j=min{max(dpi-1,x-1, dpi,j-x) + 1} 1<=x<=j
我们可以清晰的看到,dpi,j 是一个关于楼层j的单调递增函数,但鸡蛋数i固定下来时,楼层j越高,所需要的操作数也会变多,因此,在上述转移方程中,dpi-1,x-1 项是一个随x增加而单调递增的函数,而dpi,j-x 是一个随x的增加而单调递减的函数,而我们需要求得的是,找到一个位置它的最大值是所有位置中最小的
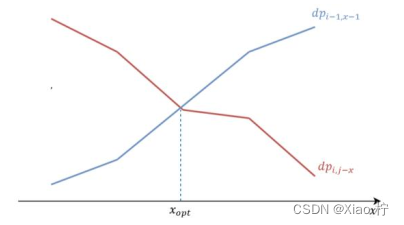
从上图中我们可以轻松找到那个位置,即为两个函数dpi-1,x-1, dpi,j-x 变化曲线相交的点x0即可,x0可保证两个函数的最大值最小。
但由于dpi-1,x-1 和dpi,j-x 都是离散函数,我们两个函数的交点可能不是整数。所以我们选择去找离这两个函数交点左右两侧最近的整数,然后取二者更优的解作为x0。 也就是说, 我们需要找到最大的满足 dpi-1,x-1 ≤ dpi,j-x 的𝑥1,以及最小的满足 dpi-1,x-1 ≥ dpi,j-x 的𝑥2,其中能保证𝑥1 + 1 = 𝑥2。
二分优化:
我们在所有满足条件的 𝑥 上进行二分查找。对于状态𝑑𝑝𝑖,𝑗而言, 𝑥 范围是 [1,𝑗]中的任一整数。 在二分查找的过程中,假设当前这一步我们查找到了𝑥𝑚𝑖𝑑,如果 𝑑𝑝𝑖-1,𝑥𝑚𝑖𝑑-1 ≥ 𝑑𝑝𝑖,𝑗-𝑥𝑚𝑖𝑑,那么真正的𝑥𝑜𝑝𝑡一定在 𝑥𝑚𝑖𝑑 的左侧,否则真正的𝑥𝑜𝑝𝑡在 𝑥𝑚𝑖𝑑的右侧。
算法伪代码
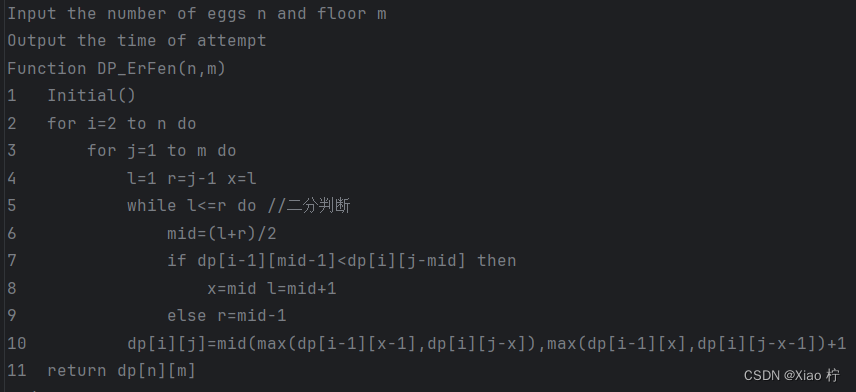
算法复杂度分析
对于n个鸡蛋和m层楼的跌落实验:
时间复杂度:状态数量一共为n*m个,由于使用的是二分查找,每个状态找特定位置x0需要O(lgm)的时间,所有时间复杂度一共为O(nmlgm)
空间复杂度:由于所有的状态需要 O(1)的空间存储,所以空间复杂度为𝑂(nm)
数据测试
为降低偶然性,我们对每组数据重复测试 10 次再取平均值,并利用公式T=T0*n*m*lgmn0*m0*lgm0 绘制理论运行时间曲线。
当M=10000, 20000, …, 100000, N=20时
| 楼层 m | 10000 | 20000 | 30000 | 40000 | 50000 | 60000 | 70000 | 80000 | 90000 | 100000 |
| 操作数 | 14 | 15 | 15 | 16 | 16 | 16 | 17 | 17 | 17 | 17 |
| 实际耗时ms | 59.6 | 127.7 | 194.2 | 269.4 | 332.4 | 417.9 | 478.4 | 557.4 | 620.9 | 700.4 |
| 理论耗时ms | 59.6 | 128.1 | 200.1 | 274.2 | 350.0 | 427.1 | 505.3 | 584.4 | 664.3 | 745.0 |
当M=50000, N=11, 12, …, 20时
| 鸡蛋数 n | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 操作数 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 |
| 实际耗时ms | 178.6 | 193.3 | 208.7 | 223.4 | 240.9 | 265.1 | 273.5 | 296.0 | 324.5 | 337.4 |
| 理论耗时ms | 178.6 | 194.3 | 211.0 | 227.3 | 243.5 | 259.7 | 276.0 | 292.5 | 308.4 | 324.7 |
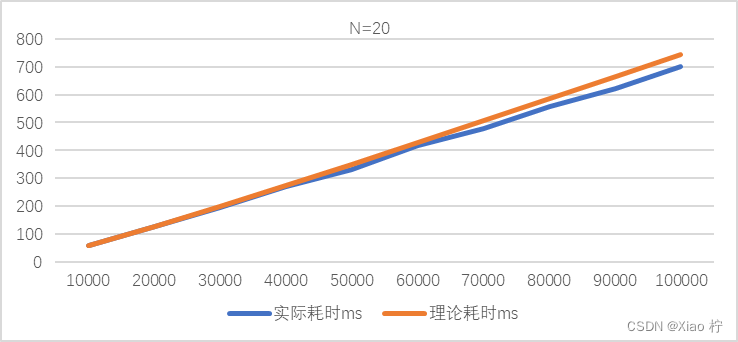
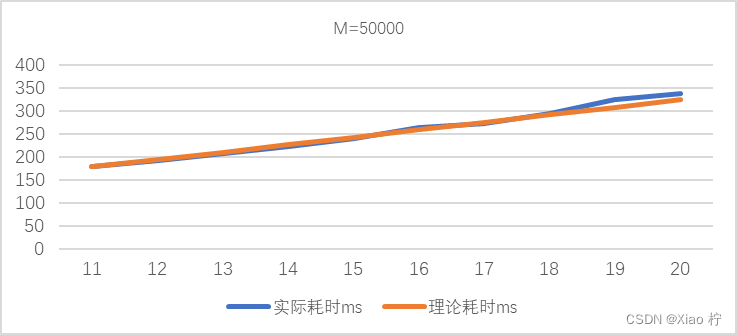
两条曲线基本吻合,故二分优化的动态规划算法的时间复杂度满足𝑂(nm log m),曲线上升趋势也符合复杂度的分析
单调决策优化的动态规划法
算法描述
对于动态规划方程:
dpi,j=min{max(dpi-1,x-1, dpi,j-x) + 1} 1<=x<=j
如果我们固定鸡蛋数ⅈ, 随着楼层数𝑗的增加, 状态转移方程中dpi,j-x 这一项的值也会增加, 而对于状态转移方程中dpi-1,x-1 这一项,它的值是不变的,因为它和 𝑗无关。在二分优化的过程中,我们知道dpi-1,x-1 随着𝑥单调递增,而dpi,j-x 随着𝑥单调递减,那么当𝑗增加时, dpi,j-x 对应的函数折线图在每个整数点上都是增加的, 如下图所示。 因此在dpi-1,x-1 不变的情况下, 随着𝑗增加, x0是单调递增的
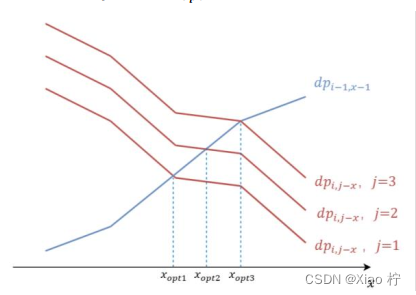
与实验2中求中间区域的最短路径相同,对于楼层j,我们寻找特定位置x0是并不需要对1~j进行二分查找,而是在之前x0的基础上进行递增查找,如此一一对应的查找,均摊下来的时间复杂度为O(1)
算法伪代码描述
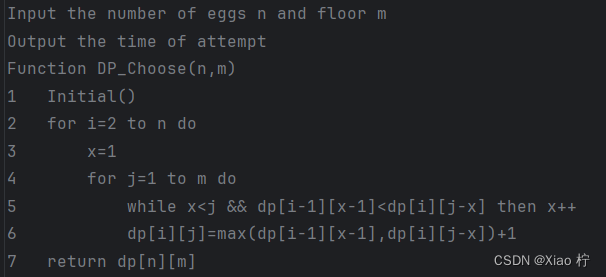
算法复杂度分析
对于n个鸡蛋和m层楼的跌落实验:
时间复杂度: 状态变量依然是n*m个, 每个状态找扔鸡蛋的楼层𝑥𝑜𝑝𝑡均摊下来的转移时间复杂度是𝑂(1), 所以时间复杂度一共为𝑂(nm)。
空间复杂度:由于所有的状态需要 O(1)的空间存储,所以空间复杂度为𝑂(nm)
数据测试
为降低偶然性,我们对每组数据重复测试 10 次再取平均值,并利用公式T=T0*n*mn0*m0 绘制理论运行时间曲线。
当M=10000, 20000, …, 100000, N=20时
| 楼层 m | 10000 | 20000 | 30000 | 40000 | 50000 | 60000 | 70000 | 80000 | 90000 | 100000 |
| 操作数 | 14 | 15 | 15 | 16 | 16 | 16 | 17 | 17 | 17 | 17 |
| 实际耗时ms | 3.9 | 10.1 | 12.4 | 16.9 | 24.4 | 28.5 | 29.5 | 31.1 | 36.9 | 40.6 |
| 理论耗时ms | 3.9 | 7.8 | 11.7 | 15.6 | 19.5 | 23.4 | 27.3 | 31.2 | 35.1 | 39.0 |
当M=50000, N=11, 12, …, 20时
| 鸡蛋数 n | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 操作数 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 |
| 实际耗时ms | 10.1 | 13.9 | 12.2 | 13.7 | 16.0 | 15.2 | 16.1 | 19.2 | 18.9 | 19.2 |
| 理论耗时ms | 10.1 | 11.0 | 11.9 | 12.8 | 13.7 | 14.6 | 15.6 | 16.5 | 17.4 | 18.3 |


蓝色曲线为决策单调性优化的动态规划算法实际运行时间拟合曲线,橙色曲线为决策单调性优化的动态规划算法理论运行时间拟合曲线,实际时间在理论时间上下波动,两条曲线基本吻合,故决策单调性优化的动态规划算法的时间复杂度满足𝑂(nm)。
空间降维优化
算法分析
对单调决策优化的动态规划法观察可以发现,状态在转移时只涉及第i−1层与第i层,第i−1层以前的状态已经不需要了,我们考虑不保存之前的状态以节省空间。为此,我们可以用两个一维数组分别表示第i−1层与第i层,从而代替整个二维数组。这样转换对于时间复杂度是没有影响的,而空间复杂度便为了O(n)。
算法伪代码描述
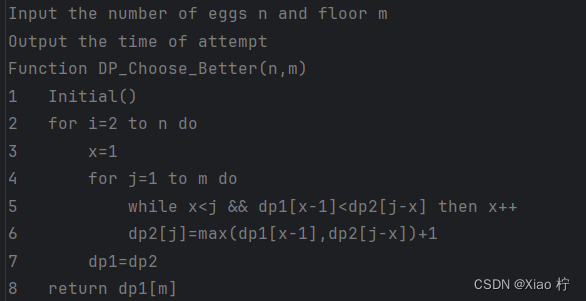
数据测试
为降低偶然性,我们对每组数据重复测试 10 次再取平均值,并利用公式T=T0*n*mn0*m0 绘制理论运行时间曲线。
当M=10000, 20000, …, 100000, N=20时
| 楼层 m | 10000 | 20000 | 30000 | 40000 | 50000 | 60000 | 70000 | 80000 | 90000 | 100000 |
| 操作数 | 14 | 15 | 15 | 16 | 16 | 16 | 17 | 17 | 17 | 17 |
| 实际耗时ms | 1.84 | 3.25 | 2.01 | 6.96 | 7.68 | 5.89 | 7.19 | 7.46 | 8.38 | 12.34 |
| 理论耗时ms | 1.84 | 3.68 | 5.52 | 7.36 | 9.2 | 11.04 | 12.88 | 14.72 | 16.56 | 18.4 |
当M=50000, N=11, 12, …, 20时
| 鸡蛋数 n | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 操作数 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 |
| 实际耗时ms | 5.0 | 5.4 | 6.4 | 7.4 | 9.3 | 7.5 | 9.2 | 9.6 | 10.3 | 10.9 |
| 理论耗时ms | 5.0 | 5.4 | 5.9 | 6.4 | 6.8 | 7.2 | 7.7 | 8.3 | 8.6 | 9.2 |
将其消耗的时间与(三)中未进行空间优化的算法消耗时间进行比较,可以明显的看出,通过空间优化,程序运行的效率得到了一个较大的提升。
综合分析
将动态规划法,通过二分优化、单调决策优化、以及降维单调决策优化的测试结果进行对比分析可以看到:
当M=10000, 20000, …, 100000, N=20时

当M=50000, N=11, 12, …, 20时

从上述两个图表的消耗时间对比我们可以看出:
决策+空间dp << 二分 dp < 朴素 dp
对于朴素动态规划算法,通过填表形式保存已求解过的状态,明显提高了算法效率,在小规模数据上速度较快,但面对大规模数据,其复杂度依旧很高,并不适用
其次是二分优化 dp, 由于其在状态转移的时候使用的是二分查找, 所以对所选楼层的查找是𝑂(log𝑛)的复杂度, 因此对于原本需要𝑂(n)时间复杂度来查找的朴素 dp, 在算法效率上由有所提高。
决策单调性优化 dp 利用了状态转移过程中x0的单调性, 在找当前状态的x0时不断利用前一个x0来查找, 利用了这种单调性, 使其查找的时间复杂度均摊下来是𝑂(1), 因此算法效率上对于二分查找优化 dp 又有进一步的提升
最后是在空间上的优化,将不再需要的空间释放掉,防止内存被消耗完,并可以减少程序在搜索上消耗的时间
五、实验结论
在本次实验中,我使用了动态规划算法对鸡蛋掉落问题进行了求解
动态规划算法利用了子问题的重叠性质,对每一个子问题只解一次,而后将其解保存在一个表格中,在以后该子问题的求解时直接查表, 这种用空间换时间的方法使时间复杂度降低为了𝑂(𝑘𝑛2), 但结果还是不够优秀。 之后我们还提出了 3 种优化算法, 分别为: 二分优化、 决策单调性优化和降维优化。 最后对各个算法进行多次测试与比较, 在算法的运行时间上我们得出以下结果:
单调决策+降维优化 dp< 单调决策优化 dp < 二分优化 dp < 朴素 dp
使用单调决策加降维优化的动态规划算法在终端输出M=10000, N=1~20时的F(M, N)值为:




![[17] 使用Opencv_CUDA 进行滤波操作](https://img-blog.csdnimg.cn/direct/0b3071cbfb7048d6b71b4b57964702fb.png)