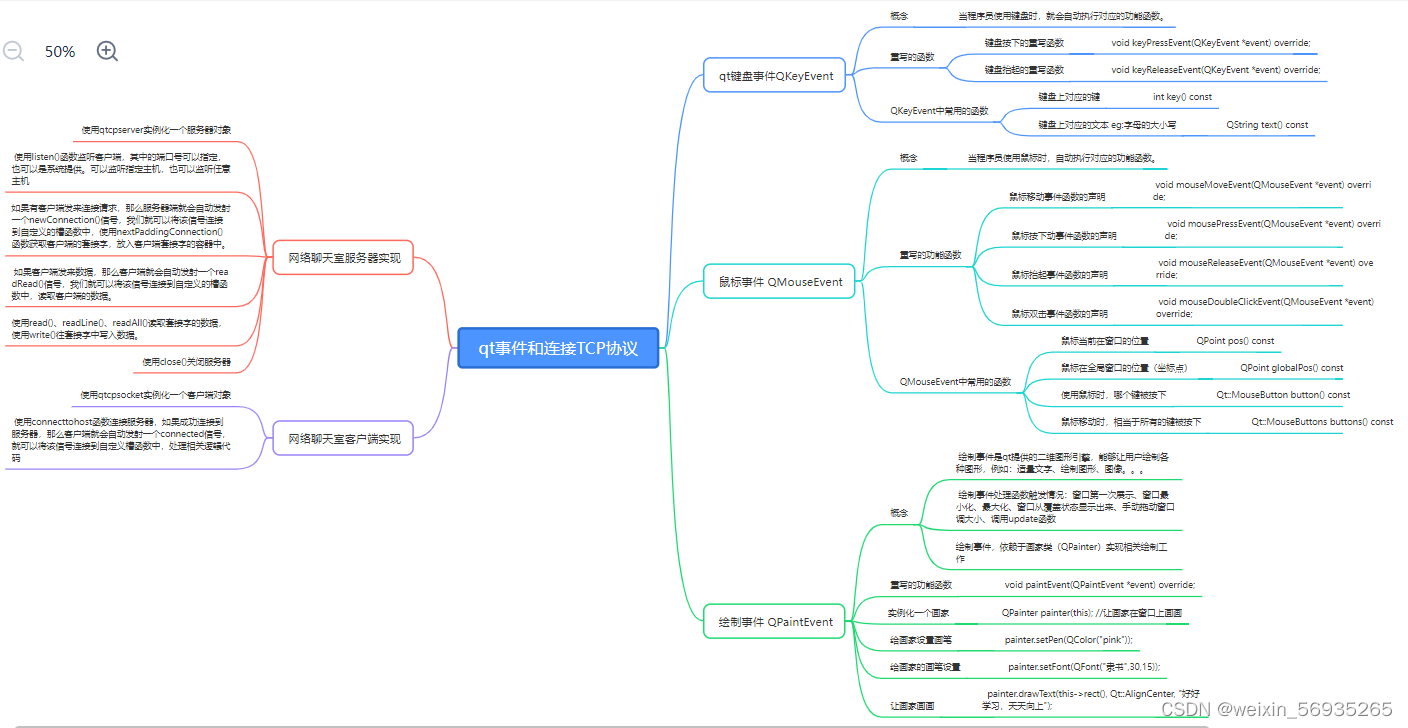
1.曲线

        曲线（Curves）在图形学中应用非常广泛，比如：相机的拍摄路径、物体的移动路径、动画曲线、矢量字体等。如下图所示，是使用曲线到矢量字体的应用，通过移动一些控制点来改变字体。

2.贝塞尔曲线

2.1 贝塞尔曲线定义

        从上图中，如果无限的放大曲线的某一块区域，任何地方都是光滑的。这就是贝塞尔曲线(Bezier Curves)。

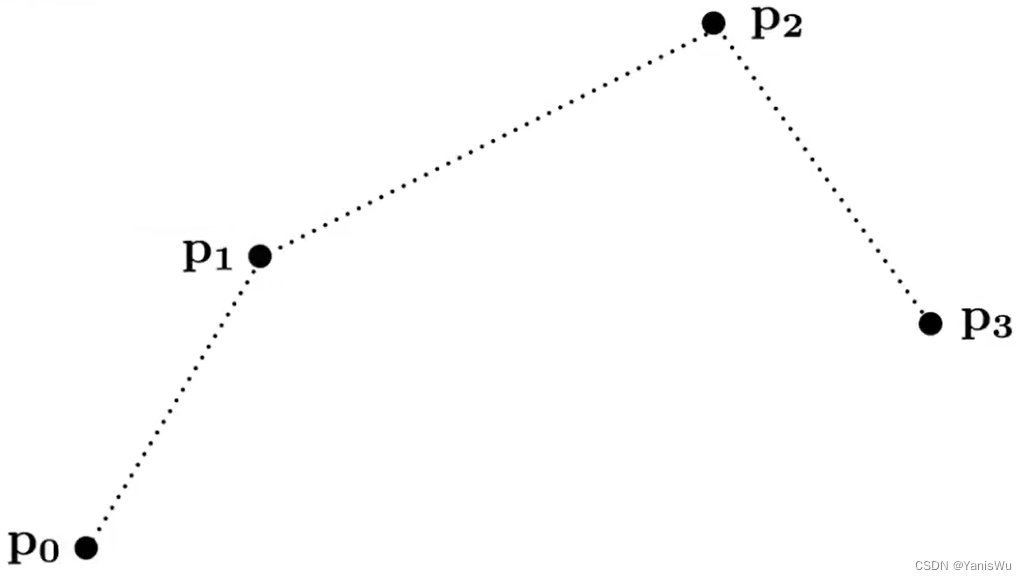
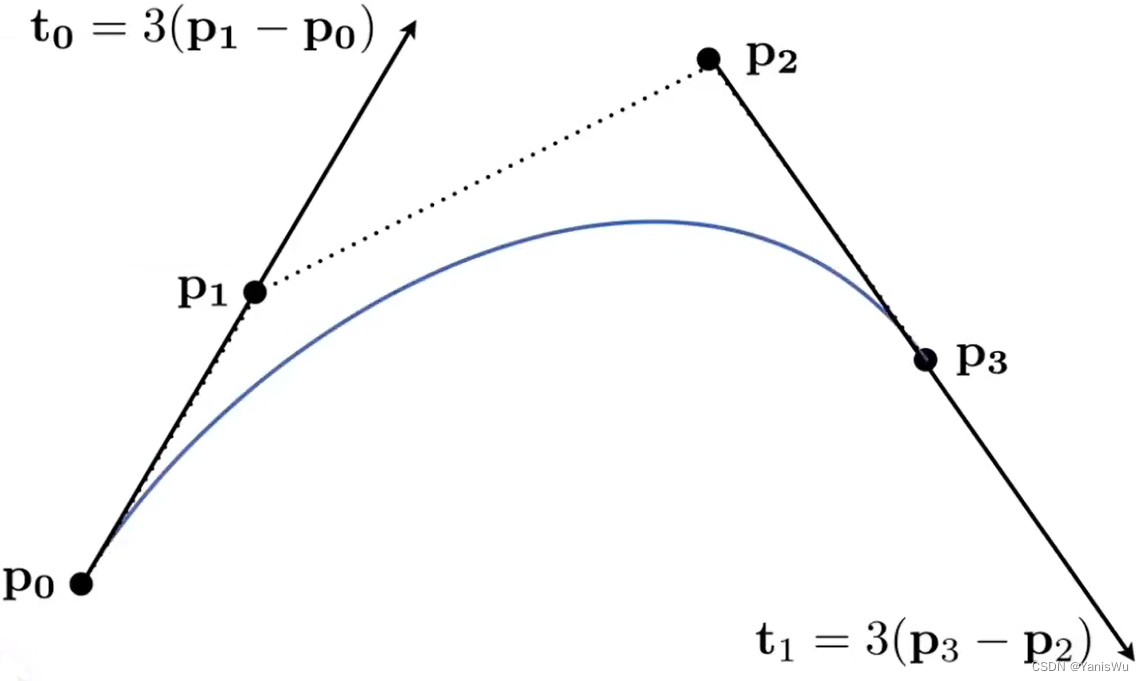
        贝塞尔曲线是通过一系列控制点进行定义的曲线。而这些控制点满足一些性质，比如要满足从P0点开始，并且沿着P0P1方向，结束沿着P2P3方向，到P3点结束。曲线不必经过所有控制点，但必须经过起始点和结束点。这样就定义了一条贝塞尔曲线，如下图所示。

2.2 绘制贝塞尔曲线

        那么，如何使用任意点绘制贝塞尔曲线呢？

        贝塞尔曲线的绘制算法是 De Casteljau's Algorithm，算法的基本思想是利用线性插值的原理，将高阶贝塞尔曲线转化为一阶贝塞尔曲线的组合。

        下面，我们以 3 个控制点绘制贝塞尔曲线的例子来进行介绍。

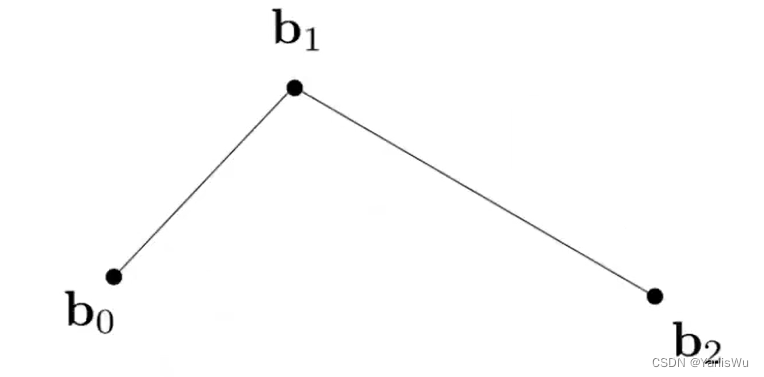
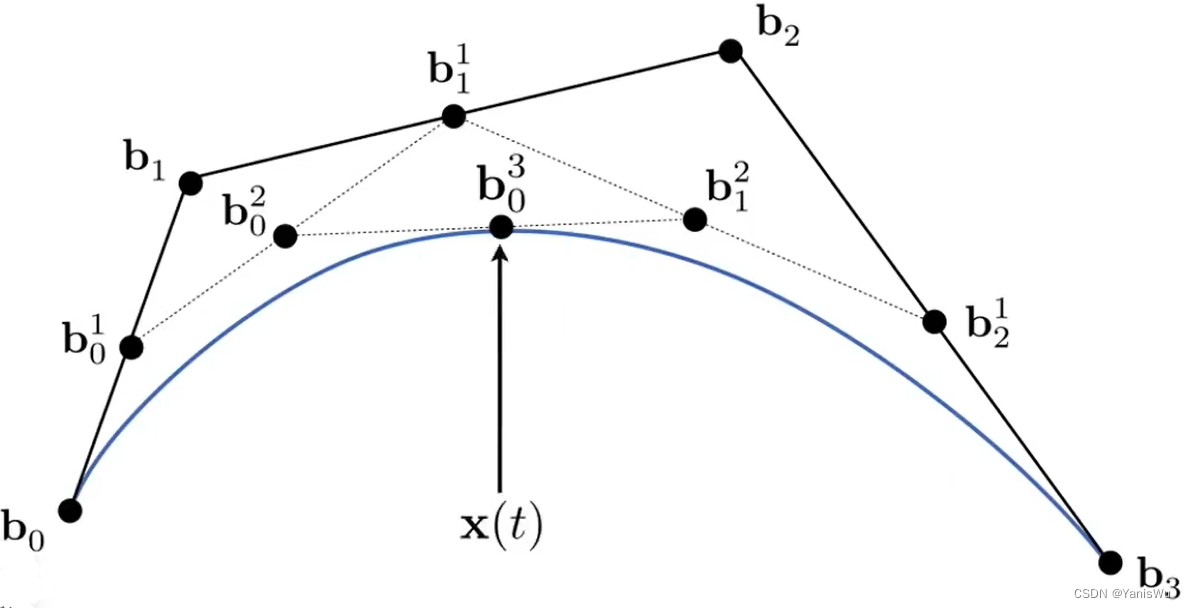
        N 个控制点绘制的贝塞尔曲线，称为 N-1 阶贝塞尔曲线。如下图所示，我们定义了 3 个控制点，由此绘制的贝塞尔曲线称之为 二阶贝塞尔曲线（Quadratic Bezier）。对于这 3 个控制点，我们首先对相邻控制点进行连线。

        定义一个变量 t，其值的范围为 [0, 1]，作为算法的输入值。当 t = 0 时，表示贝塞尔曲线起始点的输入值，当 t = 1 时，表示贝塞尔曲线结束点的输入值。所以算出 t 对应的所有点即可获得别塞尔曲线。

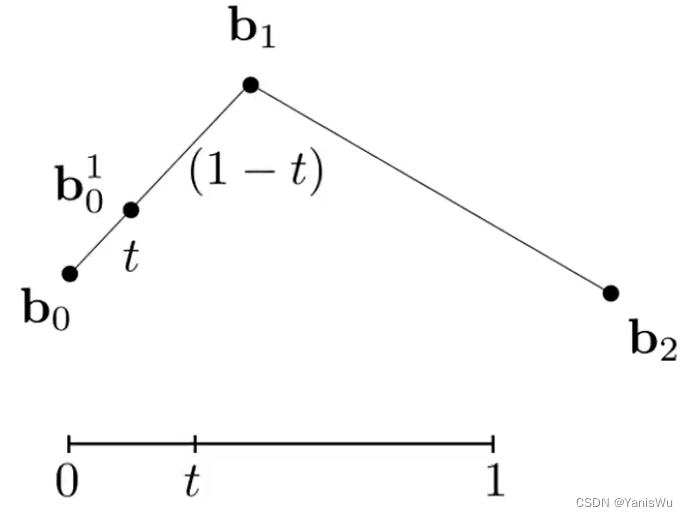
        我们在控制点所构成的各个连线上定义一个点，这个点的位置取决于 t 的值，即一个比例值。如下图所示，在 b0b1 线段上定义一个 b10 点，并在 b1b2 线段上定义一个 b11 点。

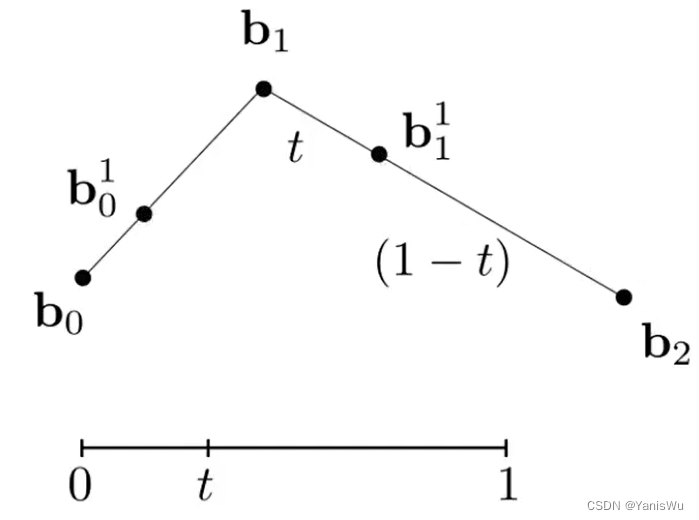
        然后，对 b10 点和 b11 点进行连线，按照上述规则，在 b10b11 线段上定义一个 b20 点，找到最后一个点就结束了。如下图所示。

        当新定义的点只有一个时，我们可以将 t 的值逐步从 0 变到 1。在这个过程中，b10、b20、b11 的位置都会随着 t 的变化而变化。对于最终的贝塞尔曲线，我们只需要关注最后定义的点 b20 的路径即可。

        当我们扩展至更多控制点时，比如 4 个控制点时，我们仍然按照上述规则来处理，将高阶贝塞尔曲线转化为一阶贝塞尔曲线的组合，最终绘制曲线。如下图所示。

        从上述可知，贝塞尔曲线也属于显式几何表示，因为显式几何表示通过直接定义或者参数定义，而这个 t 就是属于参数。

2.3 贝塞尔曲线代数公式

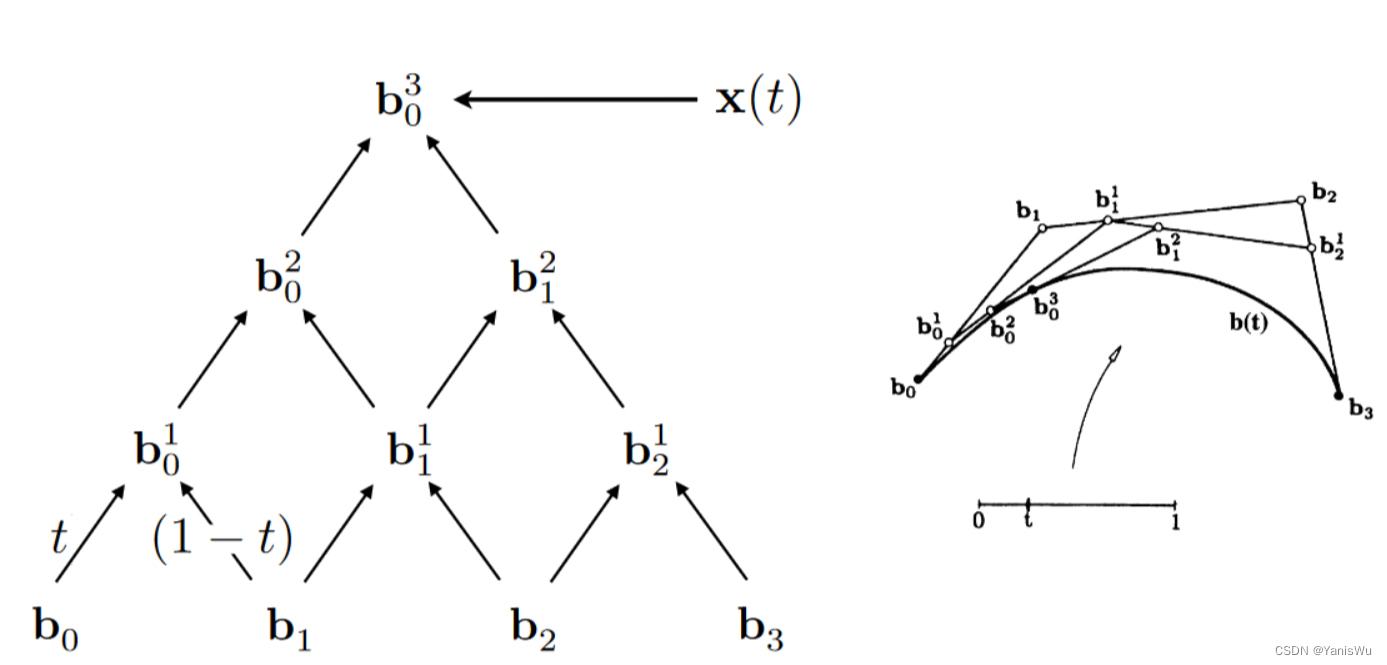
            如上图所示，De Casteljau算法给出了一个系数金字塔，从中可知通过不断线性插值得到最后一个值的算法。那么，就可以写出这个关系式，以三个控制点为例，如下图所示。

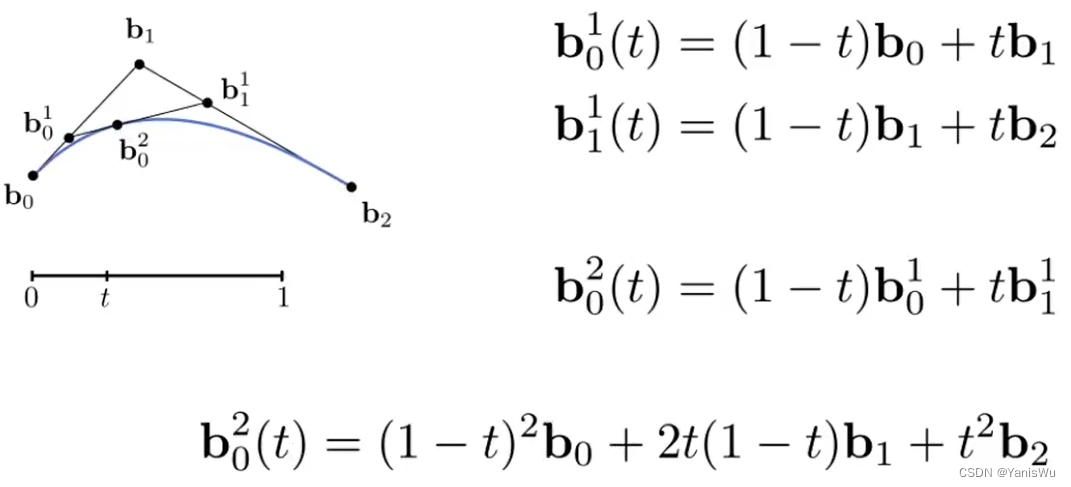
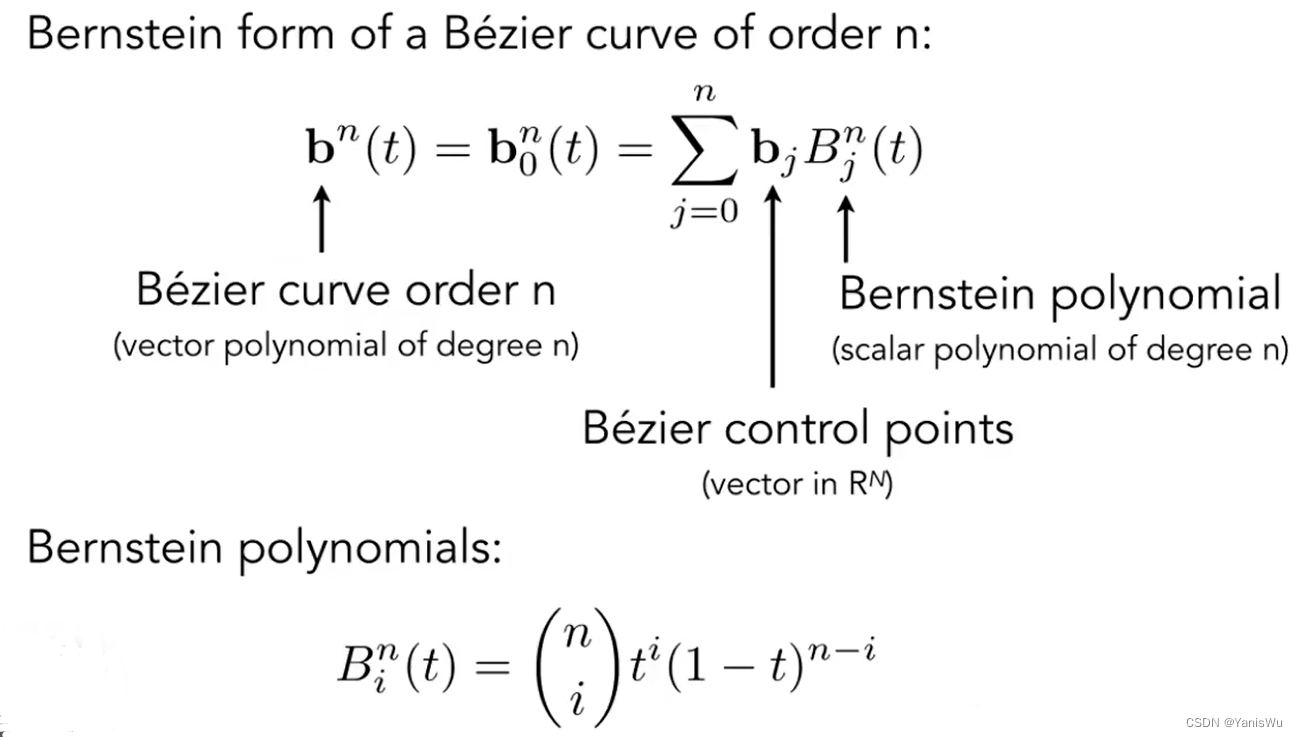
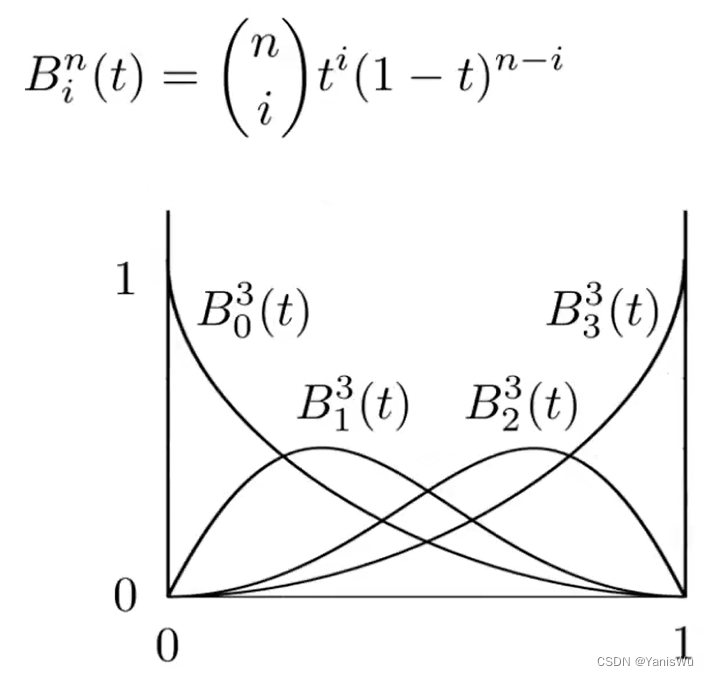
        由此，我们可以推导出 N 阶贝塞尔曲线的代数公式，如下图所示。其中，n 表示 N 阶贝塞尔曲线(n+1个控制点)， 表示控制点，为伯恩斯坦多项式（Bernstein Polynomials）。

        举个例子，假设n=3，那么可以有四个控制点，点的位置不局限于平面上，甚至在三维空间中，展开公式如下。

      对于伯恩斯坦多项式，也可得出如下关系。

2.4 贝塞尔曲线的性质

        1.一定过起点和终点。在t=0的时候一定在起点，t=1的时候一定在终点。

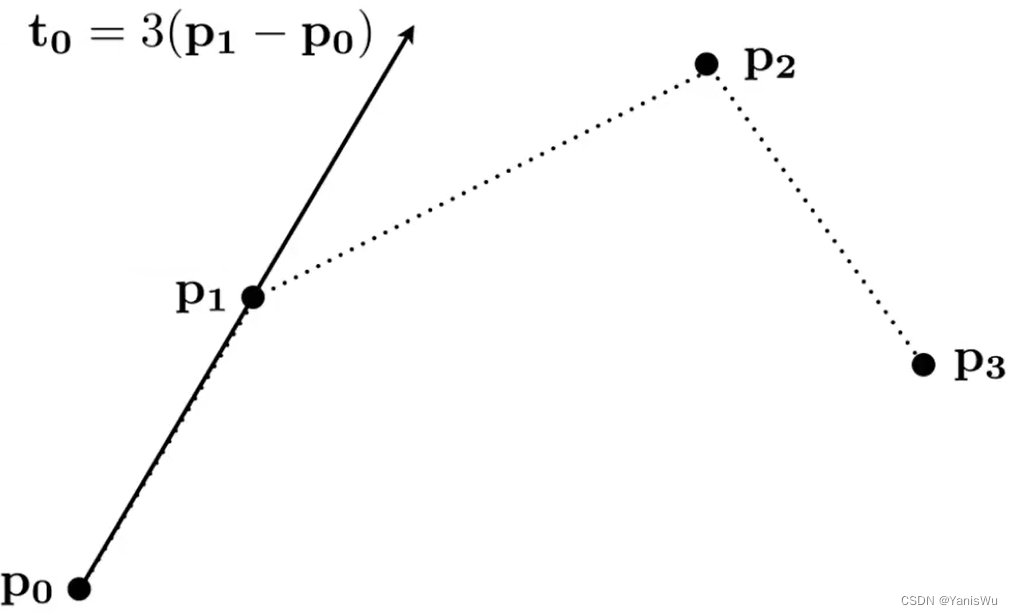
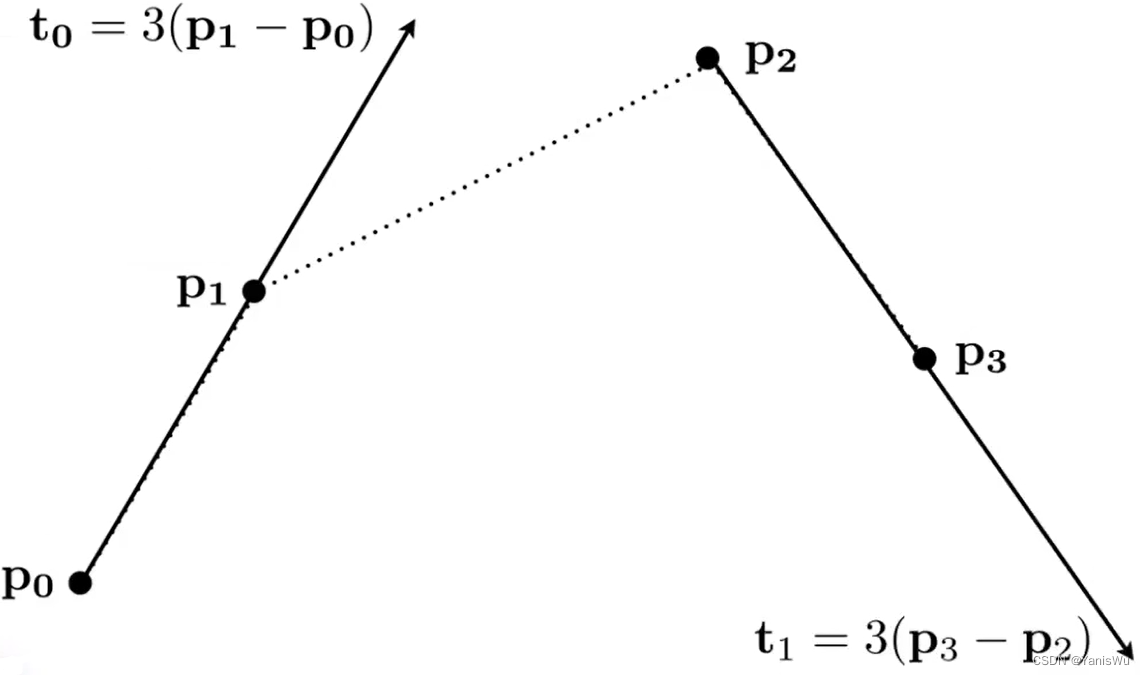
        2.起始的切线方向是由起始点和第二个点求出，结束的切线方向是由结束点和倒数第二个点求出。以四个控制举例如下，3倍只是代表4个控制点。

        3.不受仿射变换影响，受投影变换影响。

        对贝塞尔曲线上的每个控制点做仿射变换，绘制的新曲线于原曲线一样。

        在空间中绘制一条贝塞尔曲线，将控制点投影到相机看到的平面上，然后重新绘制的新曲线与原曲线不同。

        4.凸包（Convex Hull）性质：贝塞尔曲线在所有控制点的凸包范围内。如下图所示，蓝色线就是形成的凸包，凸包就是能够包围一系列几何形体的最小的凸多边形。简单理解就是一扇门上订满了钉子，然后用一块橡皮筋将外面一圈包起来，松手后橡皮筋会收缩，收缩后的外框就是凸包。

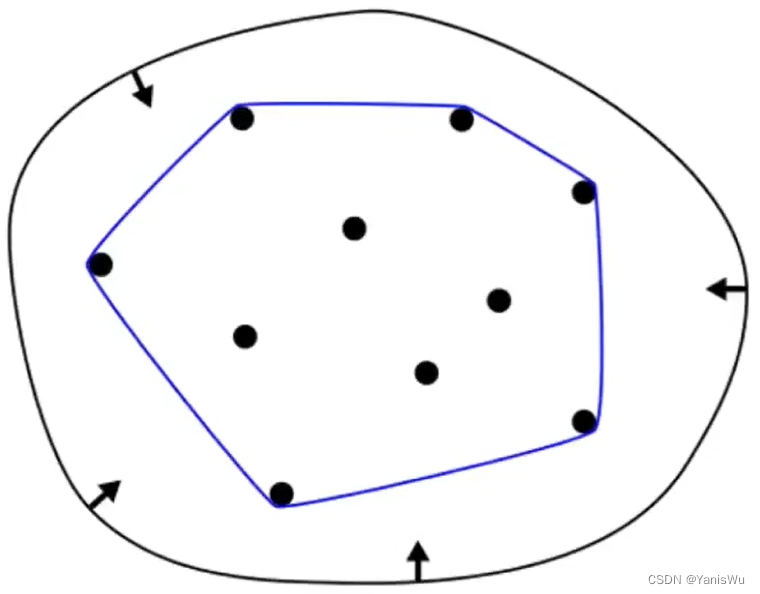
        假设有一系列从走到右排列的点，排列在一条线上，这些是绘制贝塞尔曲线的控制点，那么绘制的贝塞尔曲线应该是什么形状？根据凸包性质，这条线就是凸包，而贝塞尔曲线不能超过凸包的范围，贝塞尔曲线被限制在这条线上，所以这条线就是贝塞尔曲线。

3.分段贝塞尔曲线

3.1 定义

        如下图所示，给了11个点(n+1)，绘制一条贝塞尔曲线(蓝色线)。可以看到这条贝塞尔曲线并不直观，非常平滑，说明当控制点多的时候，贝塞尔曲线很难得到想要的形状。

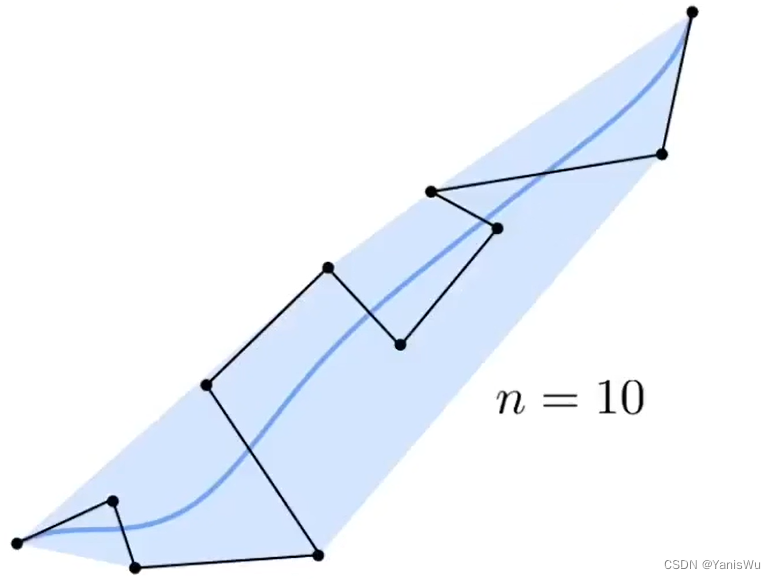
        所以，当控制点比较多时，每次用很少的控制点绘制去绘制，然后将绘制的连接成一条贝塞尔曲线。于是就有了分段贝塞尔曲线(Piecewise Bezier Curves)，即采用多条贝塞尔曲线进行串联。用4个常控制点来绘制一条贝塞尔曲线，也就是三阶贝塞尔曲线(Cubic Bezier)。如下图所示。

        在PS里钢笔工具画曲线就是这个应用。

3.2 平滑处理

        如下图所示，是一条分段贝塞尔曲线，而且每4个点绘制一条三次贝塞尔曲线。

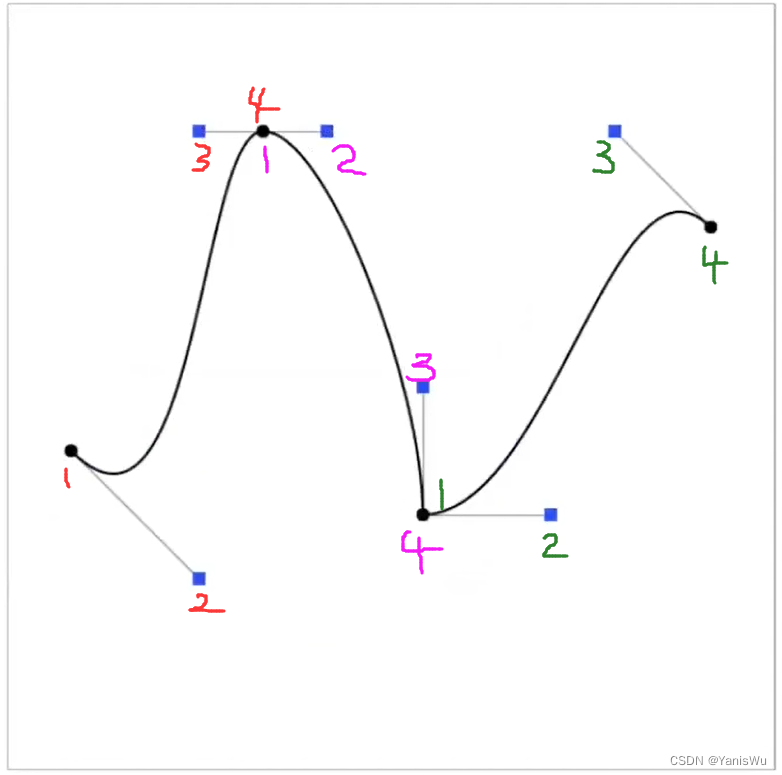
        可以发现有连接点的曲线出现了转折，不够平滑，那么如何保证连起来的曲线是平滑的呢？只要保证曲线结束的切线方向与相连曲线起始的切线相同即可(方向大小都相同)，也就是导数要连续。

        根据贝塞尔曲线的性质：三次贝塞尔曲线的起始切线的方向由第一个点和第二个点求得，结束切线的方向由第三个点和第四个点求出，并且前面有系数3。而相连的两条曲线，前一条曲线的结束点就是后一条曲线的起始点，所以需要调整前一条曲线的第三个点与后一条曲线的第二个点位置，使其切线相同。

3.3 连续性

        如下图所示，在几何上两条三次贝塞尔曲线相连通过一个控制点，这是一种最简单的连续。像这种第一段的终点等于第二段的起点叫做连续(Continuity)。

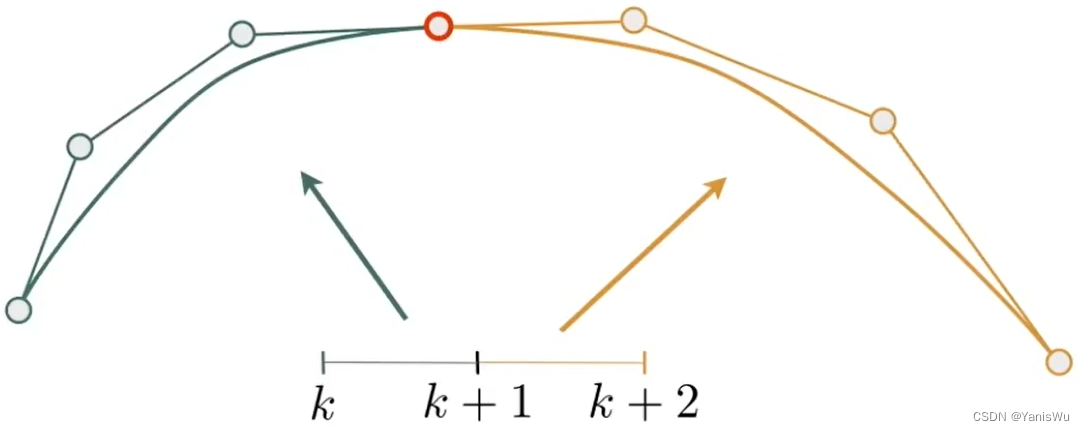
       连续关系式：。表示上一段曲线终点，表示下一段曲线起点。

       那么，在几何连续外，还需要切线的连续(切线相同，方向和大小都相同)。这叫做连续，也就是一阶导数的连续。如下图所示。

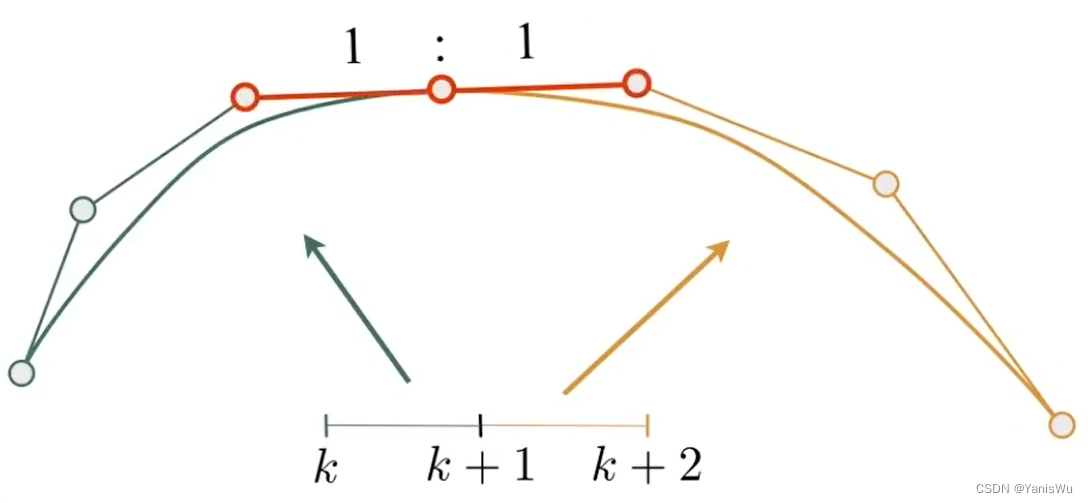
       连续关系式：。

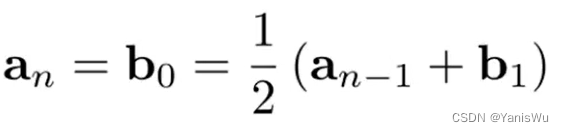       除了一阶导数连续，还有2阶导数连续，也叫做曲率连续(连续)。

        综上， 连续为两个函数在值上连续，连续为导数上的连续，为二阶导数连续，以此类推。

4.样条曲线

4.1 定义

        样条(Spline)曲线一种连续的曲线，通过一系列的控制点控制，在任意位置满足一定的连续性，也就是一定数量的连续导数(任意阶)。

        简而言之，这是一条可控的曲线。

4.2 B样条曲线

        B样条(B-Splines)是基础样条(Basis Splines)的缩写，就是基函数样条。可以理解成用伯恩斯坦多项式在时间 t 里几个不同项对不同的控制点做一个加权平均，也可以理解成不同控制点位置对伯恩斯坦多项式进行加权求和。那么，这个伯恩斯坦多项式就可以理解为基函数。基函数就是由不同函数通过不同方式组合起来可以形成别的函数。

        B样条曲线相当于是贝塞尔曲线的一个扩展。贝塞尔曲线在控制点很多的情况下，移动其中任何一个点，整个曲线在任何位置都会发生变化。假如只需要移动一个控制点改变一小段曲线的形状，也就是局部性，而B样条曲线能够满足这个功能，比分段贝塞尔曲线更方便。

        B样条需要比贝塞尔曲线更多的信息。比贝塞尔曲线更加复杂，这里不做详细介绍。