机器学习课程复习

news2024/11/22 8:14:38

参考书目：《统计学习方法》

选择题  5道  3分/道

填空题  5道  3分/道

简答题  3道  

计算题  1道  

算法设计题  1道

隐马尔可夫不考计算题

很有可能考计算题的知识点：KNN、决策树、支持向量机、聚类算法

小概率会考计算题的知识点：线性回归（最小二乘法，代公式算参数w），逻辑回归（极大似然法算参数），贝叶斯（用于分类），奇异值分解，集成学习的adaboost

1. 机器学习基本知识

机器学习课程复习——基本概念-CSDN博客

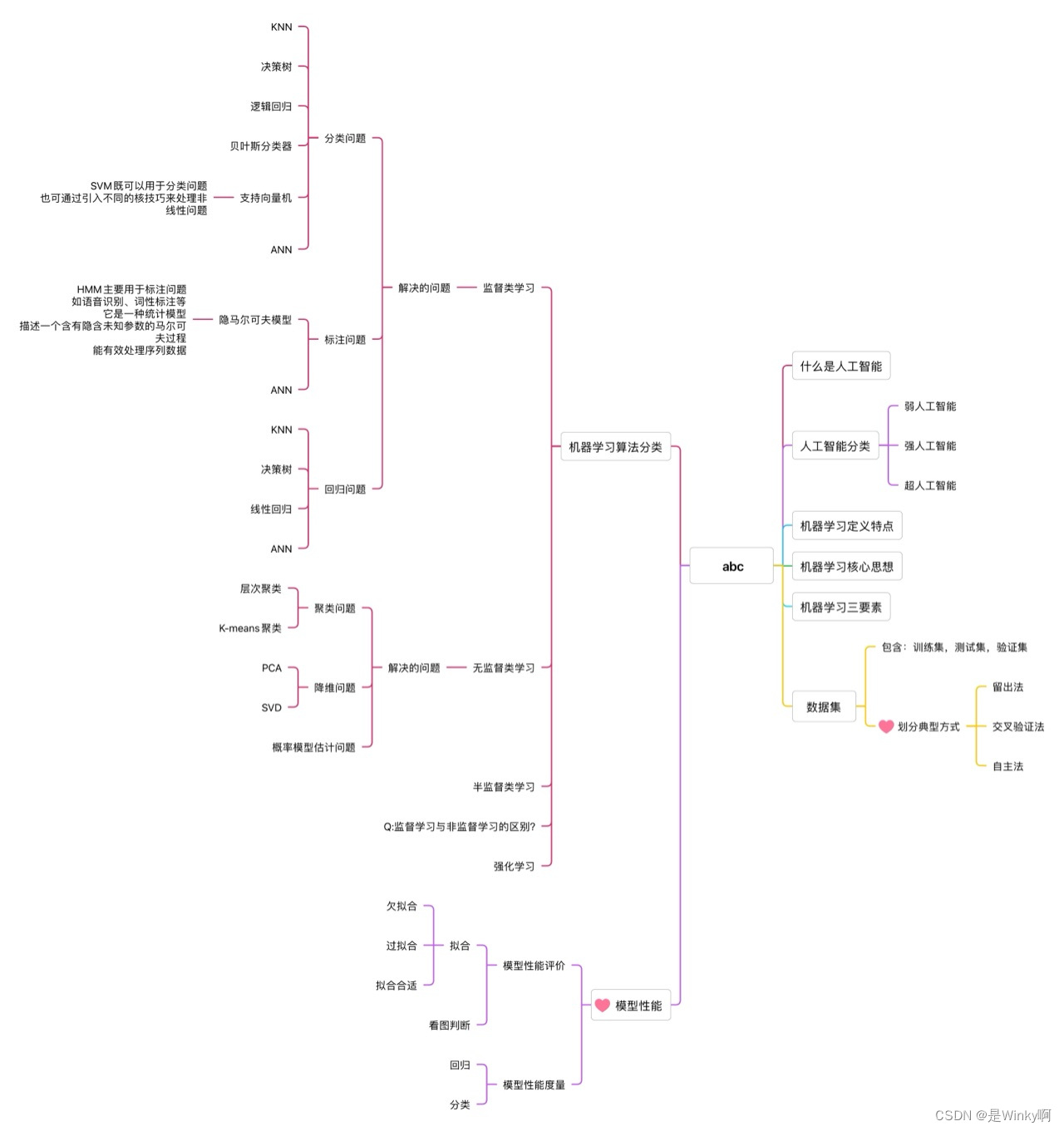b28f1cc7cf724a1a9c35c94483faae22.png2. K近邻 

机器学习课程复习——KNN-CSDN博客

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1841309.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

代码随想录——全排列（Leetcode LCR083）

代码随想录——全排列（Leetcode LCR083）

题目链接 回溯 class Solution {List<List<Integer>> res new ArrayList<List<Integer>>();List<Integer> list new ArrayList<Integer>();boolean[] used;public List<List<Integer>> permute(int[] nums) {used new bo…
阅读更多...
密码学及其应用——为什么选择接近的质数因子对RSA加密算法不安全？

密码学及其应用——为什么选择接近的质数因子对RSA加密算法不安全？

RSA加密算法是一种广泛使用的非对称加密算法&#xff0c;它的安全性依赖于大整数分解的难度。具体来说&#xff0c;RSA算法生成的公钥包含一个大整数N&#xff0c;这是两个大质数p和q的乘积。然而&#xff0c;如果这两个质数p和q太接近&#xff0c;则可以相对容易地对N进行因式…
阅读更多...
【Python机器学习实战】 | Lasso回归和弹性网回归详细分析研究

【Python机器学习实战】 | Lasso回归和弹性网回归详细分析研究

&#x1f3a9; 欢迎来到技术探索的奇幻世界&#x1f468;‍&#x1f4bb; &#x1f4dc; 个人主页&#xff1a;一伦明悦-CSDN博客 ✍&#x1f3fb; 作者简介&#xff1a; C软件开发、Python机器学习爱好者 &#x1f5e3;️ 互动与支持&#xff1a;&#x1f4ac;评论 &…
阅读更多...
【STM32】矩阵计算器

【STM32】矩阵计算器

【STM32】矩阵计算器 资料链接请在文章末尾获取~ 1.说明 使用元器件&#xff1a;stm32f103c8t6最小系统板x1&#xff0c;0.96寸OLED显示屏四角x1&#xff0c;4x4矩阵按键x1; 参考&#xff1a;正点原子有关4脚OLED驱动float型数据的驱动文件&#xff0c;CSDN有关矩阵横向扫描…
阅读更多...
网络安全：入侵检测系统的原理与应用

网络安全：入侵检测系统的原理与应用

文章目录 网络安全&#xff1a;入侵检测系统的原理与应用引言入侵检测系统简介IDS的工作原理IDS的重要性结语 网络安全&#xff1a;入侵检测系统的原理与应用 引言 在我们的网络安全系列文章中&#xff0c;我们已经涵盖了从SQL注入到端点保护的多个主题。本篇文章将探讨入侵检…
阅读更多...
八大排序————C语言版实现

八大排序————C语言版实现

Hello&#xff0c;各位未来的高级程序员们&#xff0c;大家好&#xff0c;今天我就来为大家讲解一下有关排序的内容&#xff0c;我们常见的排序就是我们接下来要讲的这八个排序&#xff0c;我们平常所说的排序有十大排序&#xff0c;我们这里的八大排序是我们生活中最为常见的八…
阅读更多...
【机器学习】：线性回归模型学习路线

【机器学习】：线性回归模型学习路线

Hi~&#xff01;这里是奋斗的小羊&#xff0c;很荣幸您能阅读我的文章&#xff0c;诚请评论指点&#xff0c;欢迎欢迎 ~~ &#x1f4a5;&#x1f4a5;个人主页&#xff1a;奋斗的小羊 &#x1f4a5;&#x1f4a5;所属专栏&#xff1a;C语言 &#x1f680;本系列文章为个人学习…
阅读更多...
探究布局模型：从LayoutLM到LayoutLMv2与LayoutXLM

探究布局模型：从LayoutLM到LayoutLMv2与LayoutXLM

LAYOUT LM 联合建模文档的layout信息和text信息&#xff0c; 预训练 文档理解模型。 模型架构 使用BERT作为backbone&#xff0c; 加入2-D绝对位置信息&#xff0c;图像信息 &#xff0c;分别捕获token在文档中的相对位置以及字体、文字方向、颜色等视觉信息。 2D位置嵌入 …
阅读更多...
DOPE-FITC在细胞定位、动态追踪等方面的应用-星戈瑞

DOPE-FITC在细胞定位、动态追踪等方面的应用-星戈瑞

DOPE-FITC作为一种荧光标记磷脂&#xff0c;在细胞生物学研究中发挥着科研作用。其荧光特性和与细胞膜的亲和性&#xff0c;使其成为细胞定位、动态追踪等方面的工具。 细胞定位 DOPE-FITC能够有效地标记细胞膜&#xff0c;使得细胞膜在荧光显微镜下呈现出明亮的绿色荧光。这种…
阅读更多...
NLP入门——复杂函数建模与链式求导

NLP入门——复杂函数建模与链式求导

复杂函数建模 前面我们研究的梯度下降法分类&#xff0c;是简单的对每类中每个子词的分数进行求和&#xff0c;统计分数最大的类别并不断调整分数来提高准确率。 我们可以修改函数模型&#xff0c;用更加复杂的函数代替sum()&#xff0c;来达到更好的学习效果。 def compute_…
阅读更多...
LLM大语言模型应用方案之RAG检索增强生成的实现步骤。

LLM大语言模型应用方案之RAG检索增强生成的实现步骤。

0.我理解的RAG 什么是RAG&#xff1f; RAG的全称是“检索增强生成模型”&#xff08;Retrieval-Augmented Generation&#xff09;。这是一种特别聪明的大语言模型。 RAG是怎么工作的呢&#xff1f; 1.检索&#xff1a;当你问RAG一个问题时&#xff0c;它会先去“图书…
阅读更多...
Dockerfile封装制作pytorch（tensorflow）深度学习框架 + jupyterlab服务 + ssh服务镜像

Dockerfile封装制作pytorch（tensorflow）深度学习框架 + jupyterlab服务 + ssh服务镜像

一&#xff1a;docker-hub官网寻找需求镜像 1.我们在https://hub.docker.com/官网找到要封装的pytorch基础镜像&#xff0c;这里我们以pytorch1.13.1版本为例 2.我们找到的这个devel版本的镜像&#xff08;我们需要cuda的编译工具&#xff09; pytorch版本是1.13.1&#xff0c;…
阅读更多...
Windows桌面运维----第四天

Windows桌面运维----第四天

1、U盘故障打不开&#xff1a; 操作方式&#xff1a;WinR打开运行&#xff0c;输入cmd确定&#xff0c;在&#xff08;C:\Users\Administrator>&#xff09;后输入chkdsk,空格&#xff0c;输入U盘盘符&#xff0c;例如F:/F&#xff0c;回车&#xff0c;等待修复完成。 2、…
阅读更多...
Bad return type in lambda expression: void cannot be converted to Unit

Bad return type in lambda expression: void cannot be converted to Unit

1.背景 当kotlin中声明需要传入一个返回值为空(Unit)的方法引用. 代码示例: 下方第二个参数为一个方法引用,(参数为BiometricPrompt.AuthenticationResult, 返回类型为Unit). object BiometricPromptUtil {private const val TAG "BiometricPromptUtil"fun cre…
阅读更多...
Day6—热点搜索词统计

Day6—热点搜索词统计

一、要求 根据用户上网的搜索记录对每天的热点搜索词进行统计&#xff0c;以了解用户所关心的热点话题。 要求完成&#xff1a;统计每天搜索数量前3名的搜索词&#xff08;同一天中同一用户多次搜索同一个搜索词视为1次&#xff09;。 二、数据 三、配置scala环境 1.下载sca…
阅读更多...
思科PAP命令笔记

思科PAP命令笔记

命令格式 含义 版权声明&#xff1a;本文为博主原创文章&#xff0c;遵循 CC 4.0 BY-SA 版权协议&#xff0c;转载请附上原文出处链接和本声明。 原文链接&#xff1a;https://blog.csdn.net/qq_44862120/article/details/115675197 ——————…
阅读更多...
动态规划——活动安排问题II（C++）

动态规划——活动安排问题II（C++）

Take it easy! 2024年6月19日 题目描述 假设有n个活动和一个资源&#xff0c;每个活动执行时都需要占用该资源&#xff0c;并且该资源在任何时间只能被一个活动所占用&#xff0c;一旦某个活动开始执行&#xff0c;中间将不能被打断&#xff0c;直到其执行完毕。每个活动i都有…
阅读更多...
数据结构--顺序表（图文）

数据结构--顺序表（图文）

顺序表的概念和特点 顺序表是一种线性数据结构&#xff0c;它由一组数据元素构成&#xff0c;这些元素具有相同的特性&#xff0c;并按照一定的顺序排列。在顺序表中&#xff0c;数据元素通常存储在连续的内存空间中&#xff0c;这使得通过索引可以直接访问到表中的任意元素。…
阅读更多...
考研计组chap2数据的表示和运算

考研计组chap2数据的表示和运算

3一、进位计数制 1.r进制 第i位表示r进制的权为i 2.进制转换 &#xff08;1&#xff09;r->10 对应位置数*权值 &#xff08;2&#xff09;2 -> 16 or 8 每三位2进制数可表示1位16进制 每四位2进制数可表示1位16进制 so 分开之后转为16进制即可 eg&#xff1a;1…
阅读更多...
欧拉函数的求解

欧拉函数的求解

欧拉函数的定义 欧拉函数的性质 性质1是性质2的特殊情况 性质1的理解&#xff1a;一个数a是质数&#xff0c;前面的数b与a的gcd一定是1 性质2的理解&#xff1a;1,2,…p,p1,p2…2p,…3p…p^k 其中以np结尾的序列重复了p^&#xff08;k-1&#xff09;次&#xff0c;每一次的循环…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023