各位CSDN的uu们你们好呀，今天我们的内容依然是关于连续函数的概念和性质及相关内容，之前的博客我们学习到了函数的连续性和函数的间断点，那今天，我们便来看看闭区间上连续函数的性质，好的，接下来就让我们进入高等数学的世界吧
一、有界性与最大值最小值定理
二、零点定理与介值定理
三、函数与极限习题课
（一）理解极限的定义
（二）掌握数列极限、函数极限的性质
（三）求极限的若干方法
1.有理函数的极限
2.有界函数*无穷小=无穷小
3.利用左、右极限相等
4.极限存在的准则
5.利用两个重要极限
6.利用等价无穷小代换（重要方法）
7.利用初等变形
8.利用数列极限与函数极限的关系
（四）无穷小阶数的比较
（五）间断点与连续性
（六）闭区间上连续函数的性质
（七）例题
一、有界性与最大值最小值定理
这个定理我们就不证明了，因为证明此定理需要用到非常复杂的实数理论
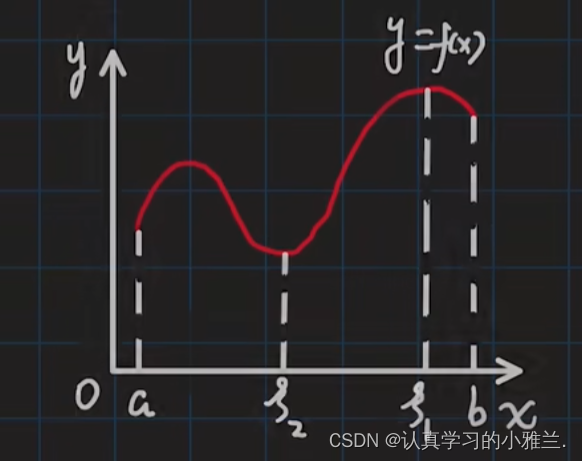
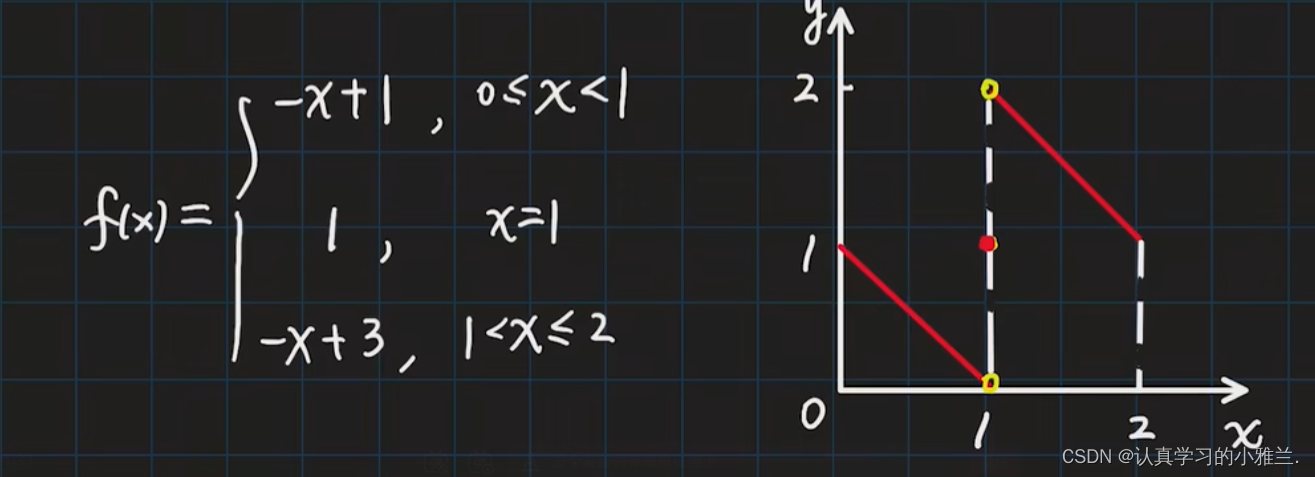对于这两个函数，在其定义域内都是既没有最大值，也没有最小值
二、零点定理与介值定理
其实，这个零点定理我们在高中应该就已经学过了，我们来复习一下，究竟什么是零点呢？
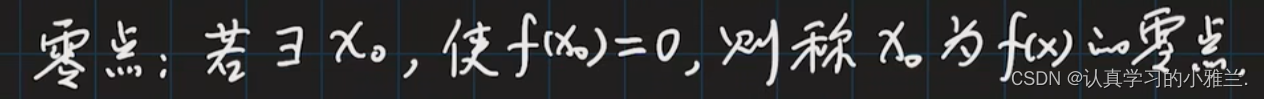
可见，零点并不是一个点，而是一个数
同样，这个定理我们也不证明了，因为比较复杂，但是，从几何上是很好理解的
这是函数图像与x轴只有一个交点的情况
这是函数图像与x轴有多个交点的情况
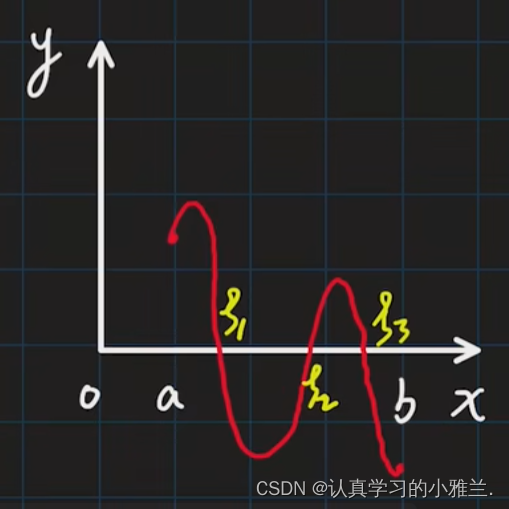
在此定理的基础上，我们很容易推出我们接下来要介绍的一个定理，那就是——介值定理
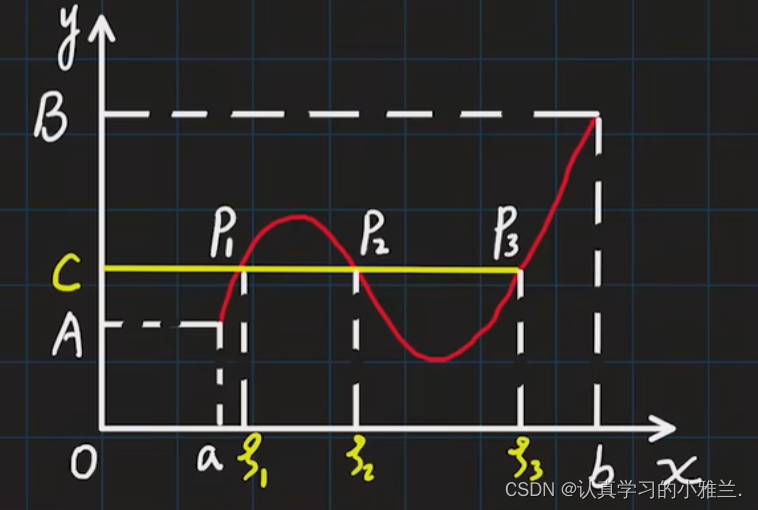
下面，来证明一下这个介值定理
然后，我们又得出了一个推论
下面，让我们来看几个例题
首先，从结论出发，构造函数
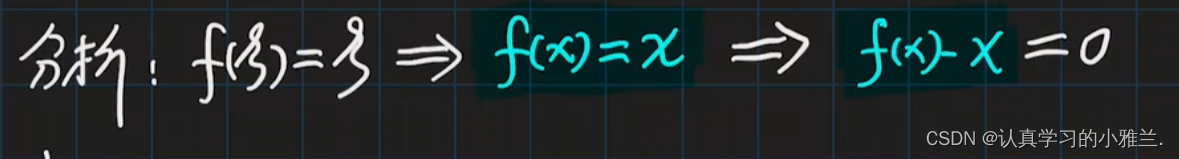
三、函数与极限习题课
1.理解极限的定义
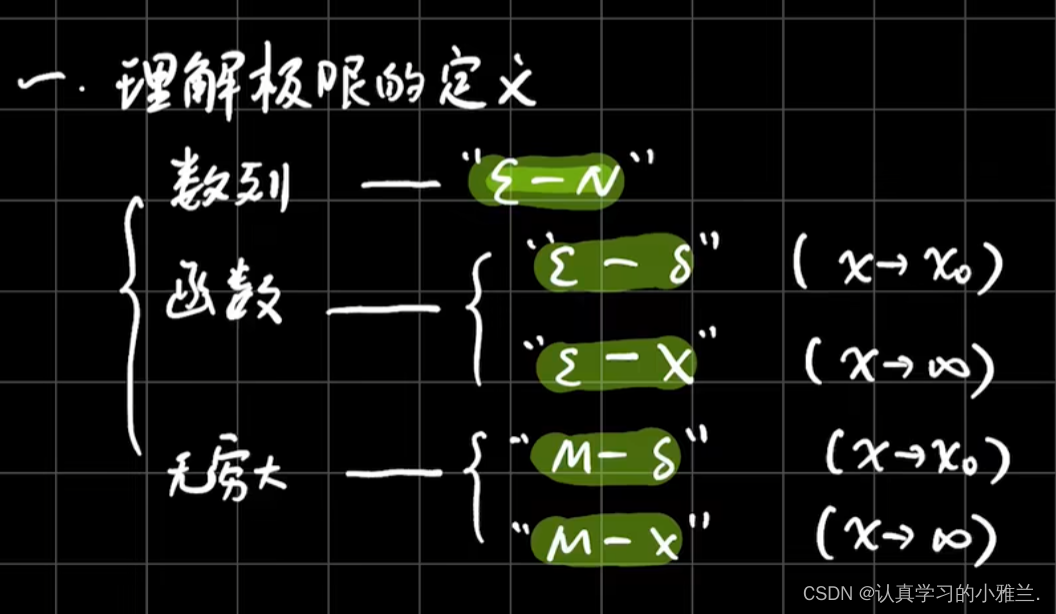
2.掌握数列极限、函数极限的性质
3.求极限的若干方法
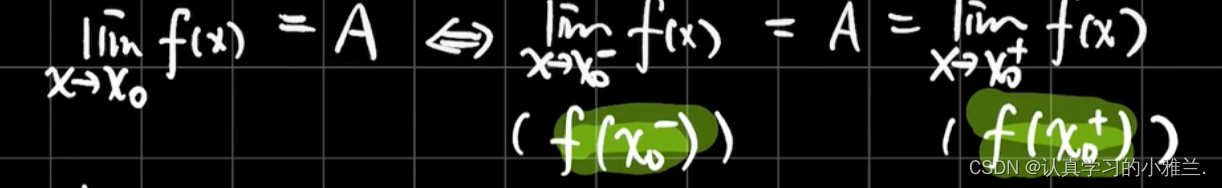
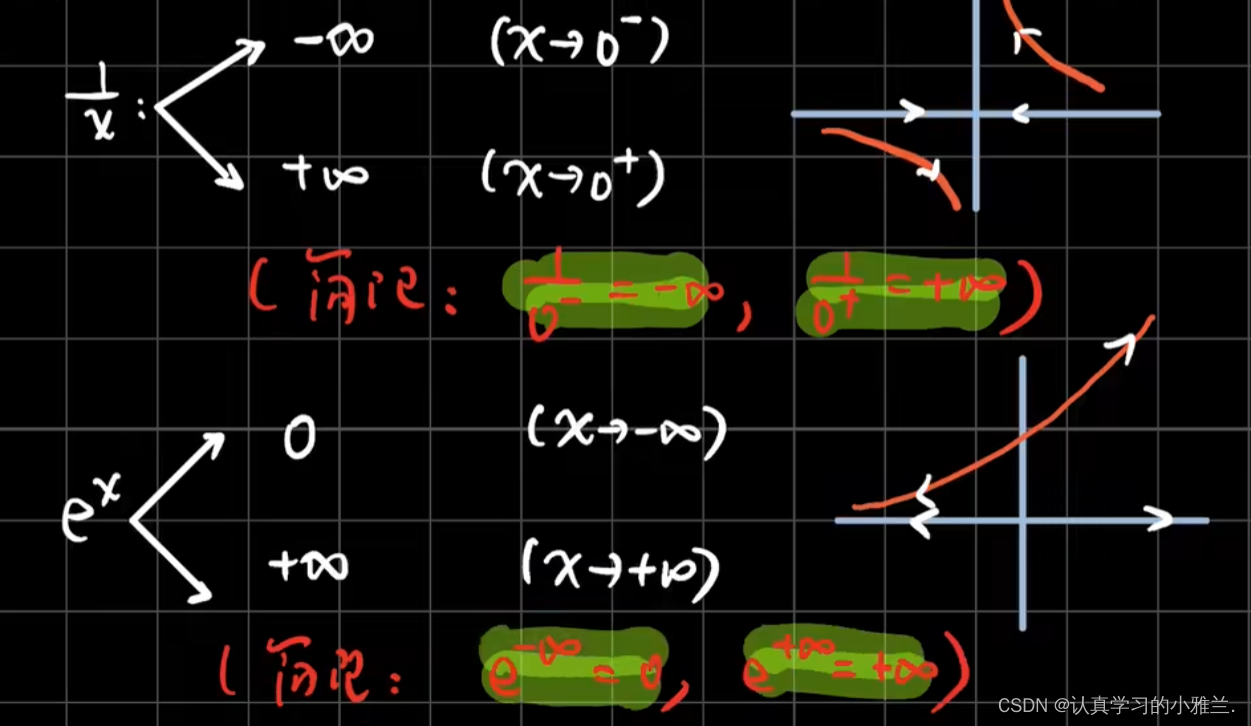
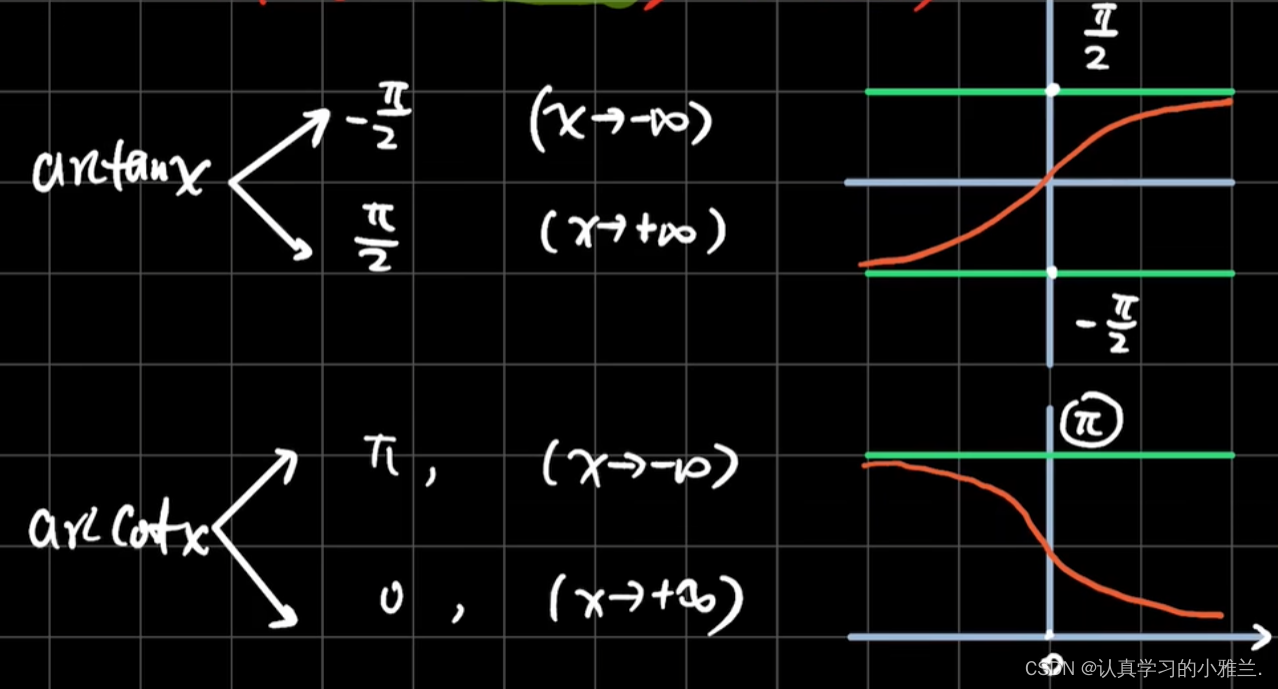
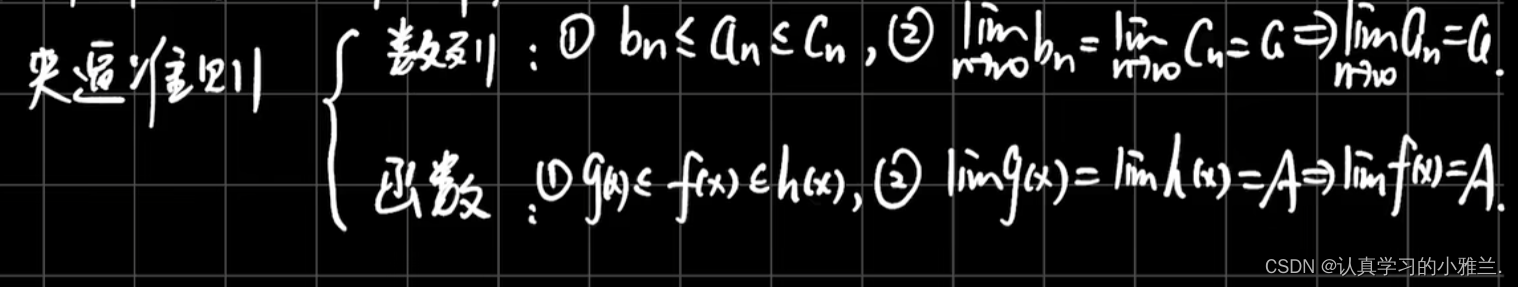
这个注意事项里面，为什么要把它划为一个问号呢？因为，在有的时候，它是成立的，而有的时候，它又是不成立的。
4.无穷小阶数的比较
5.间断点与连续性
6.闭区间上连续函数的性质
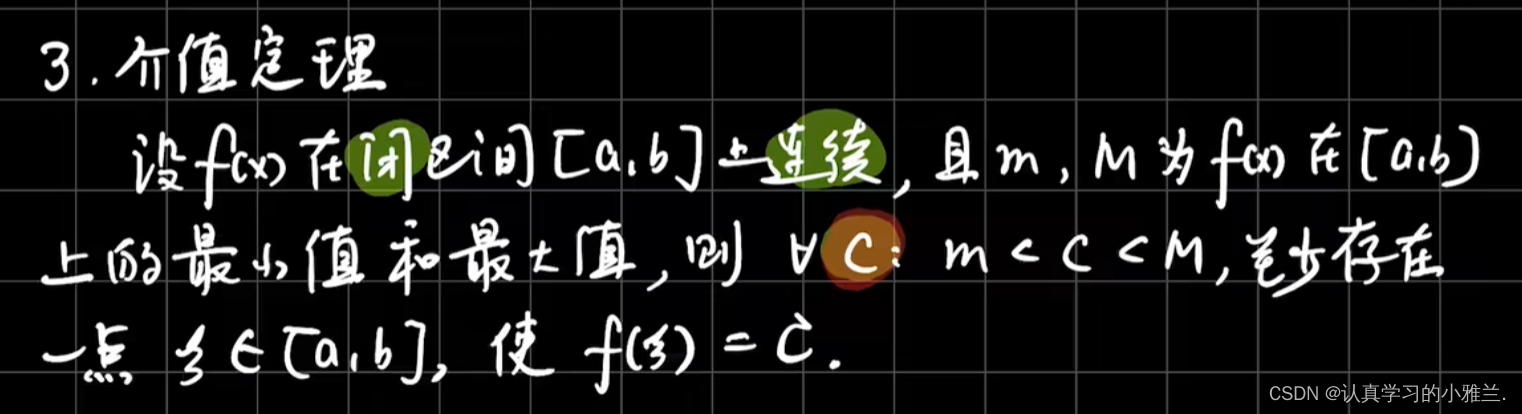
例题
所以第一个论断不正确
第二个论断也是不正确的，只能说明局部有界
所以第三个论断也是不对的
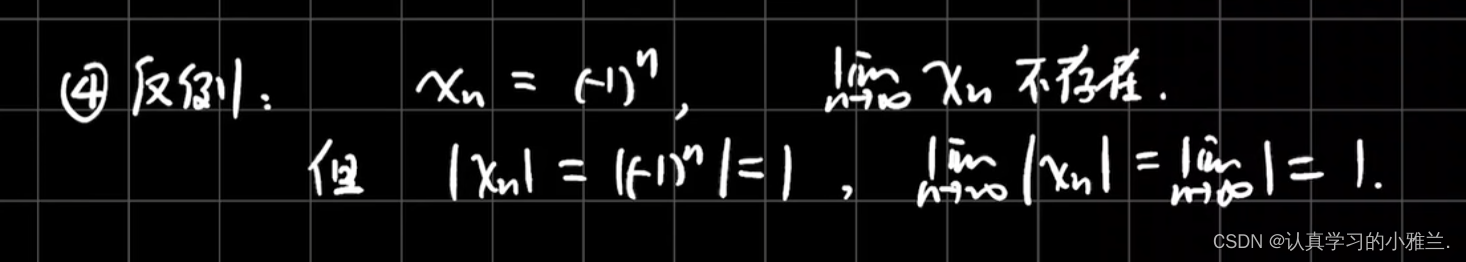
所以第四个论断也是不正确的
故，此题目正确答案选D
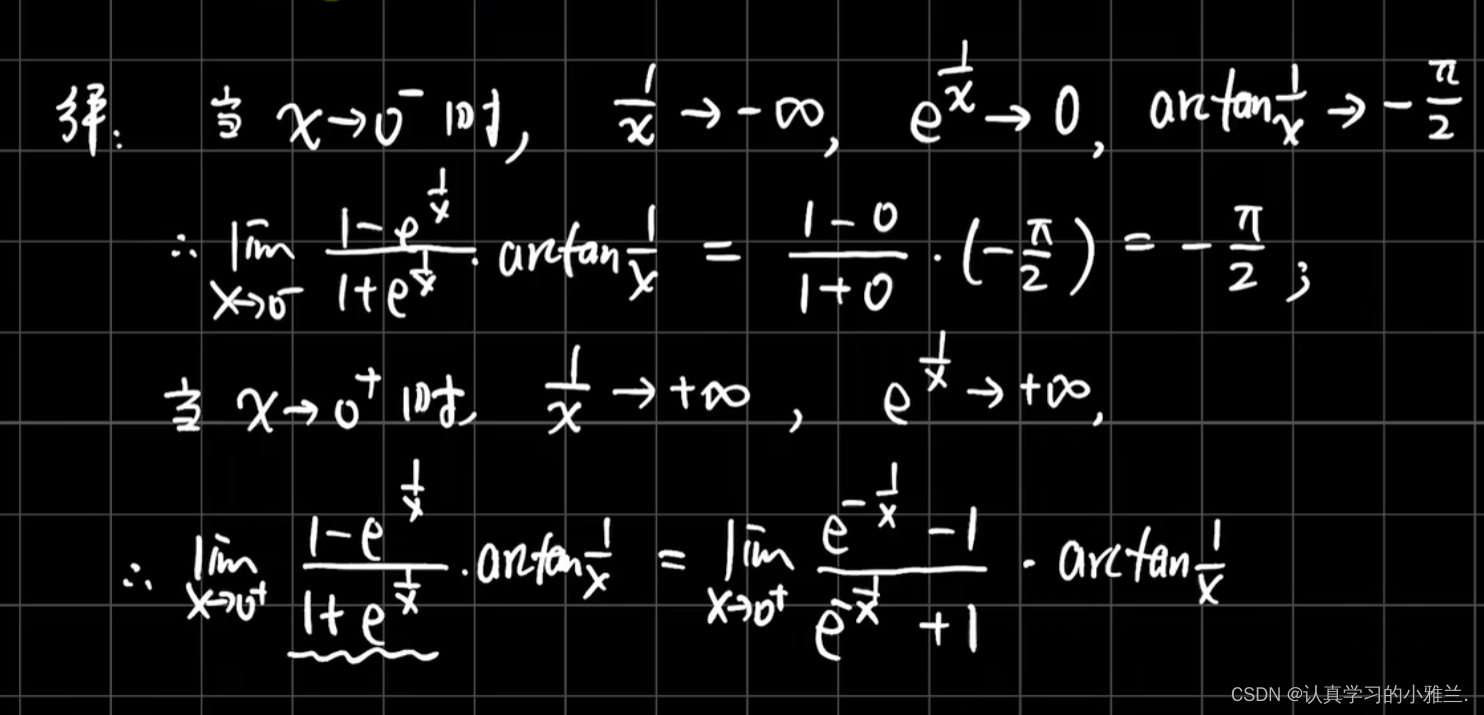
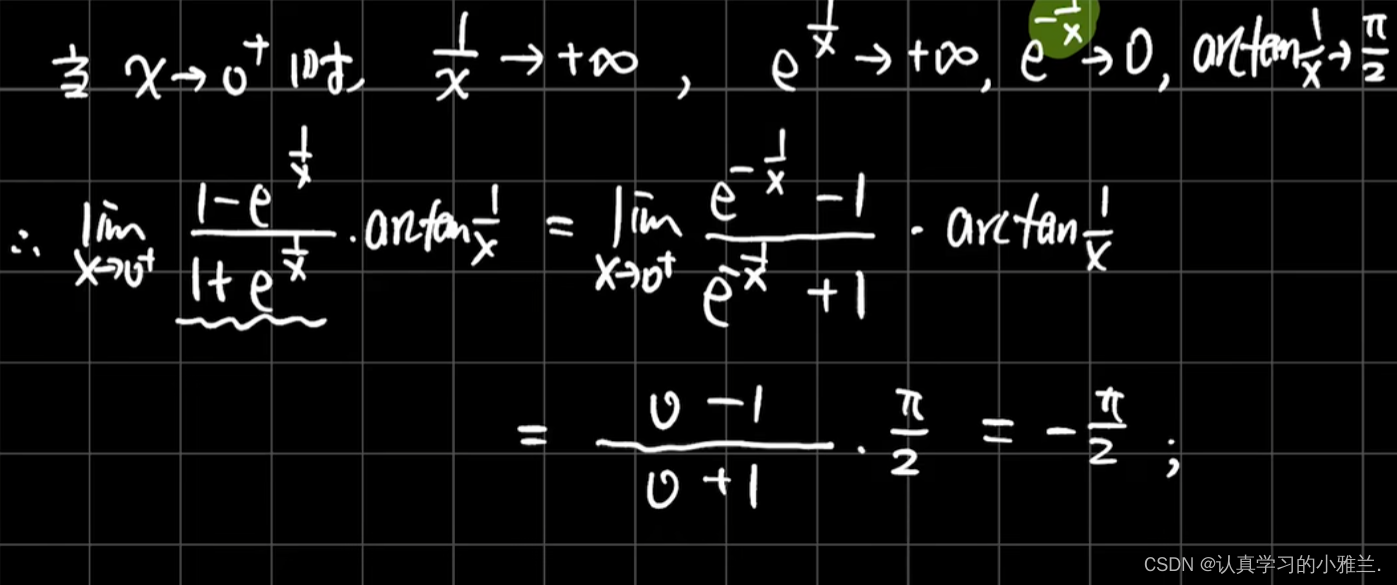
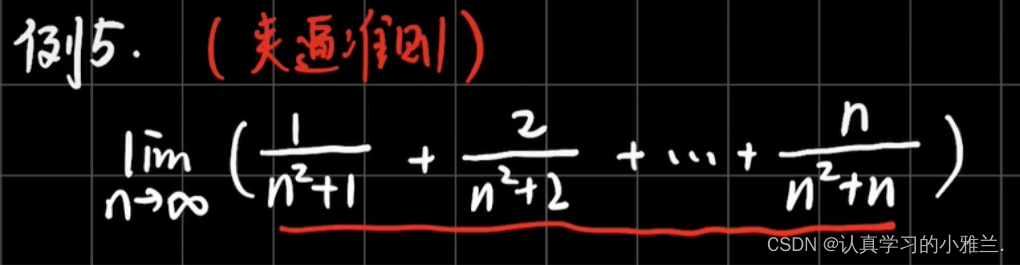
连加式
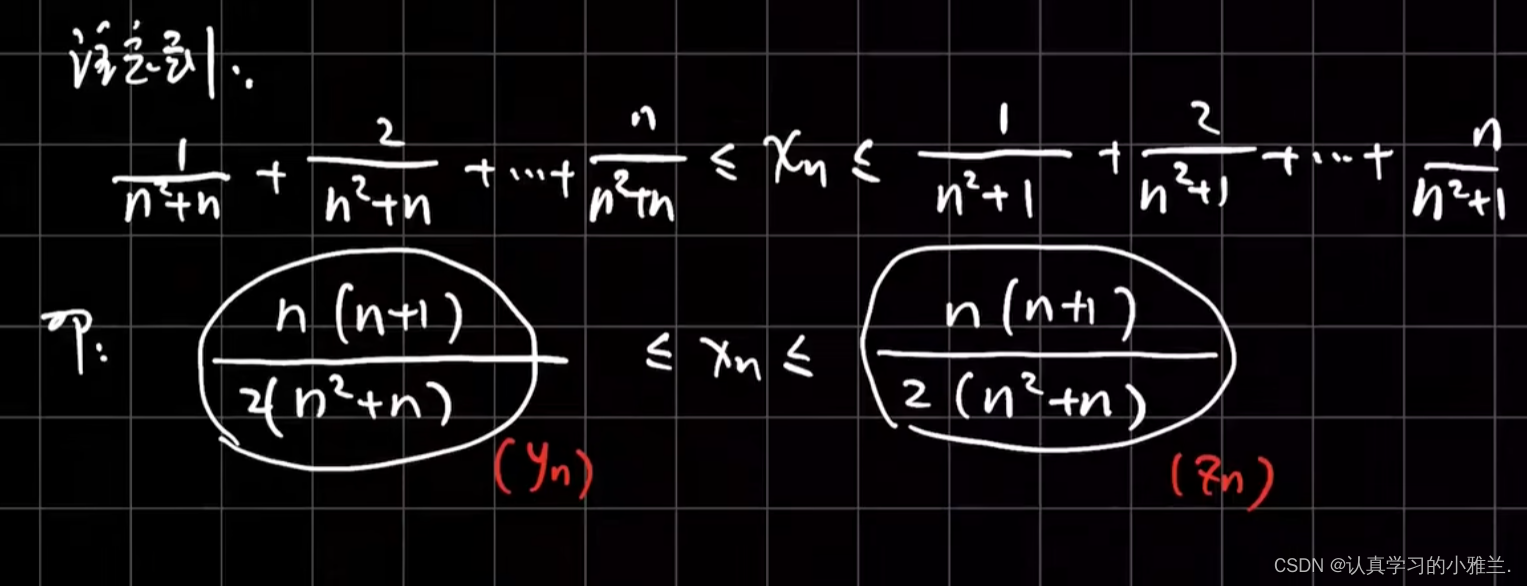
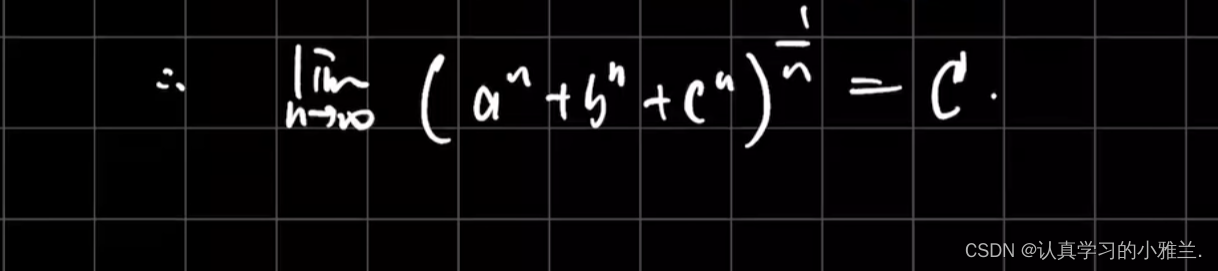我们可以把这个结论推广一下
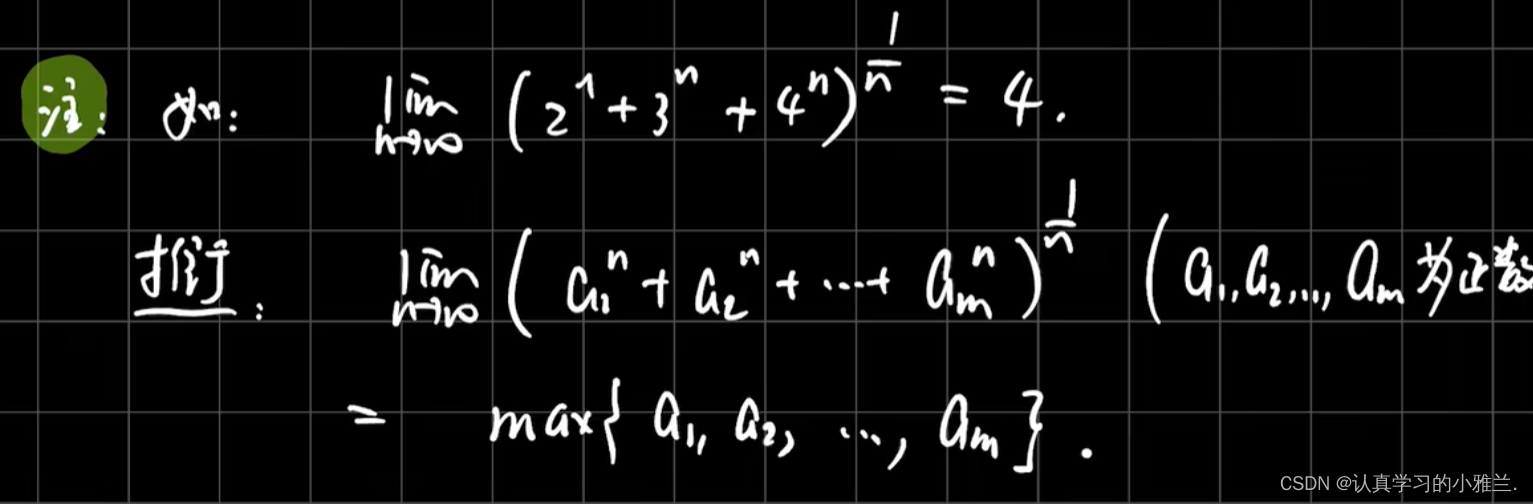
考察单调有界原理的知识点
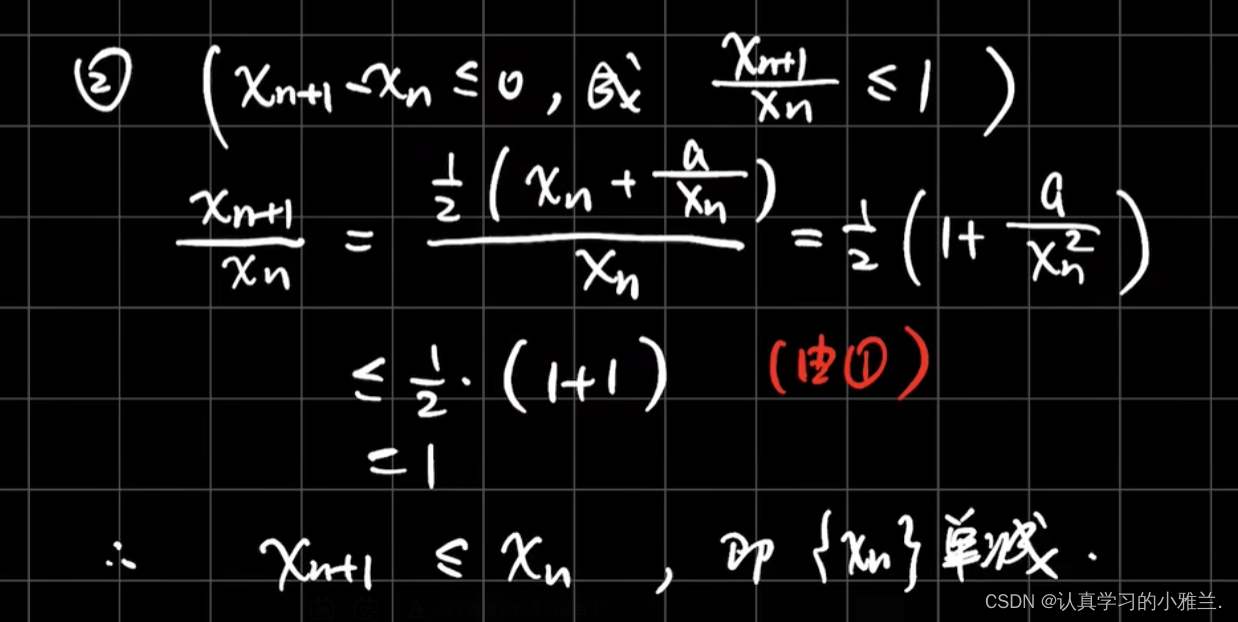
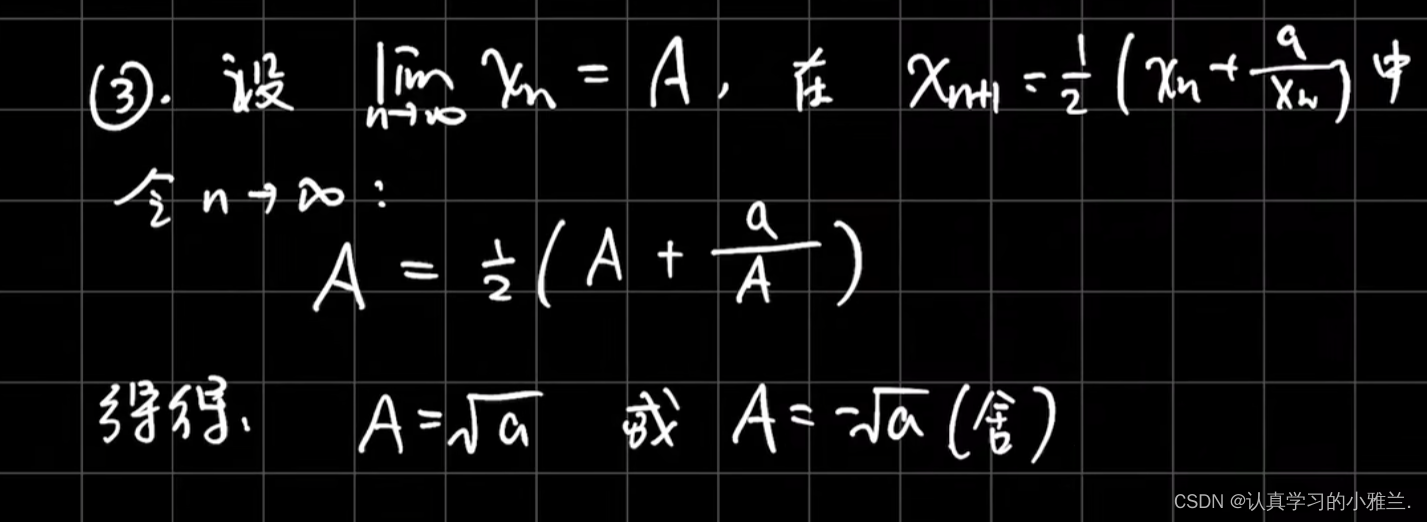因为这是一个正数列
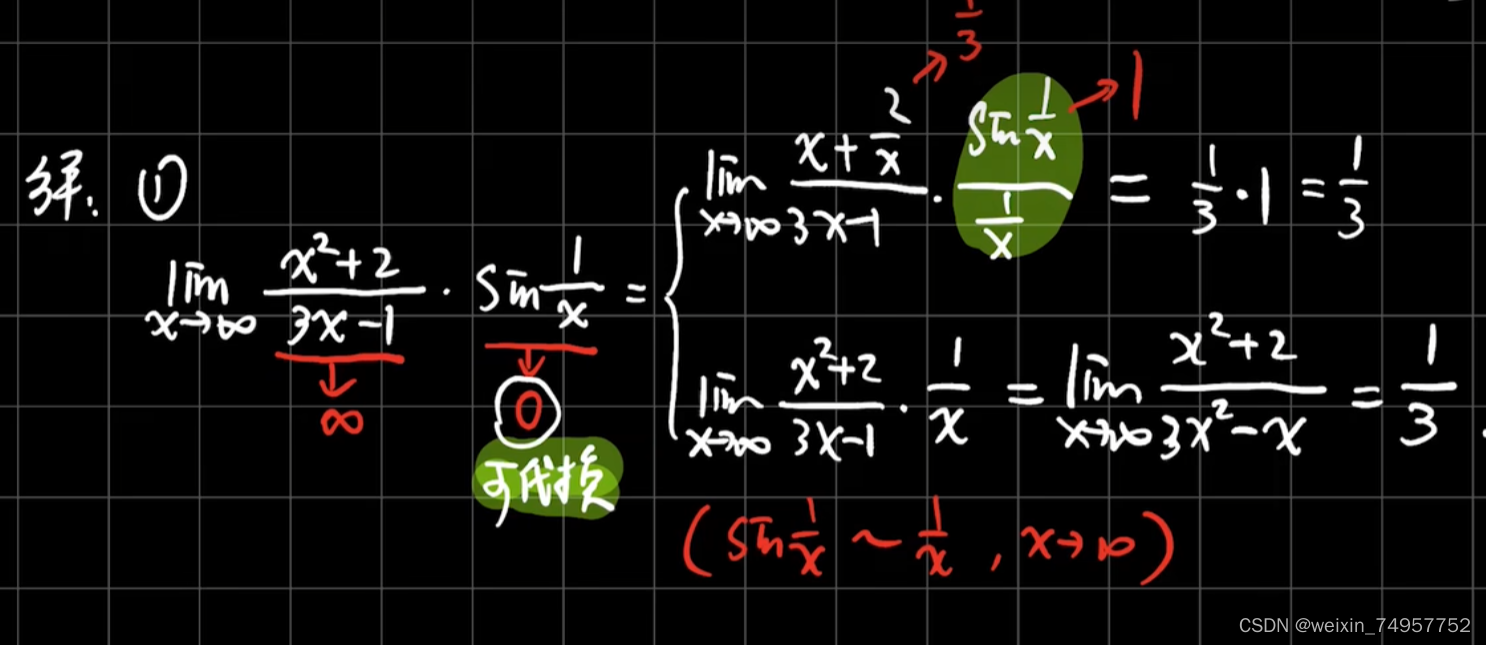
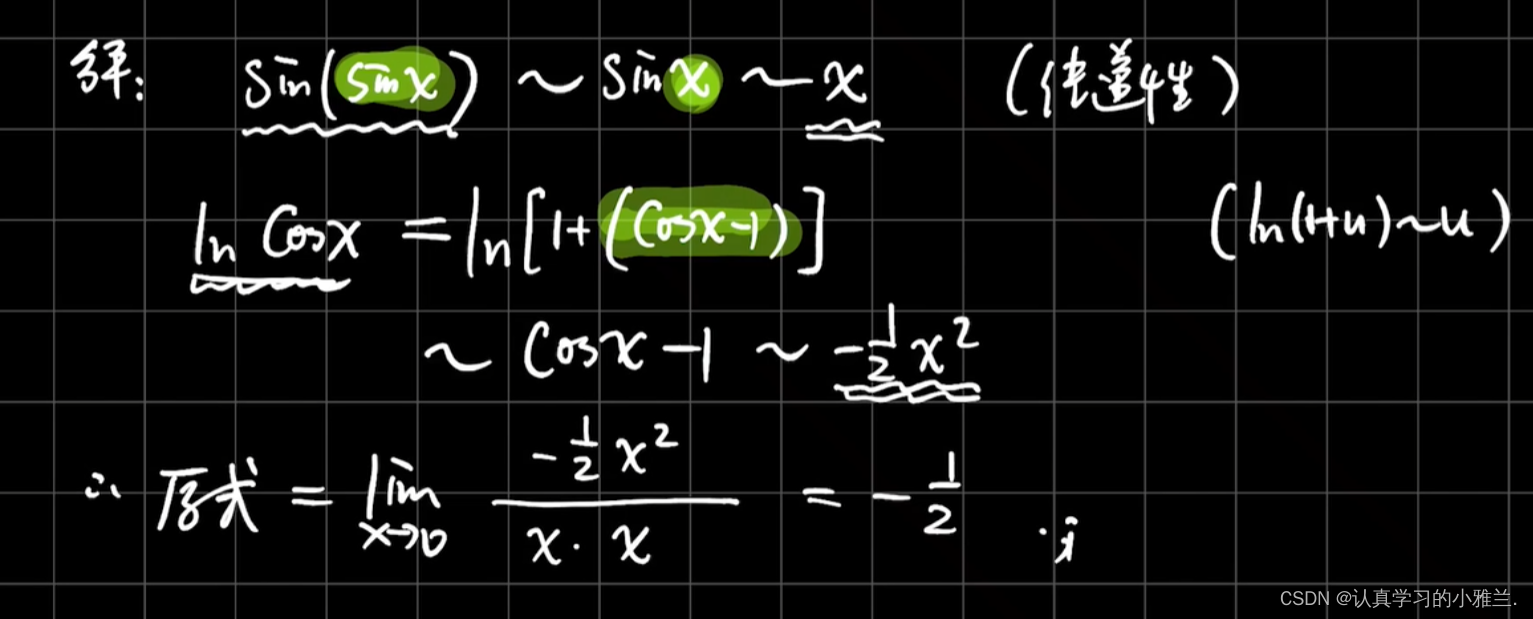
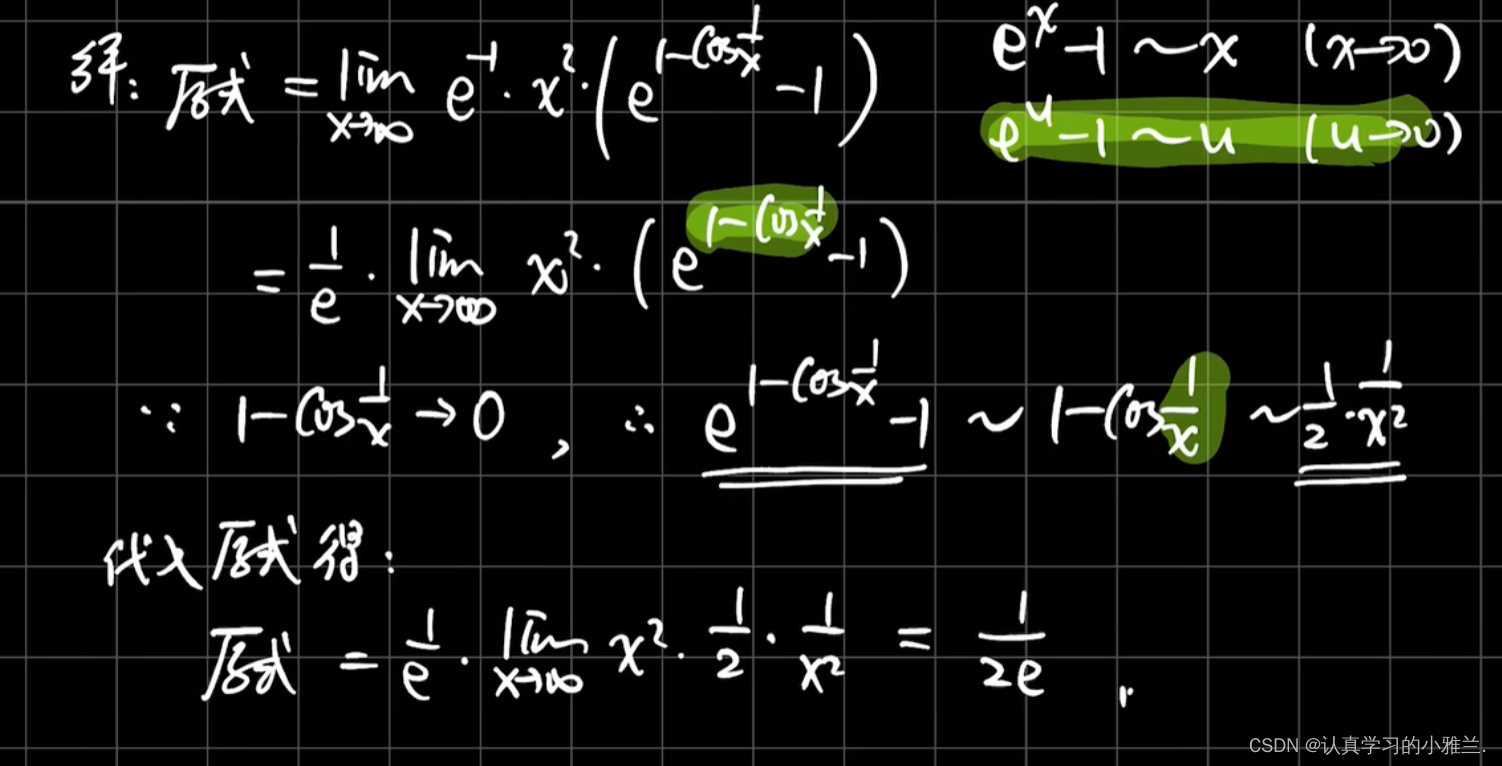
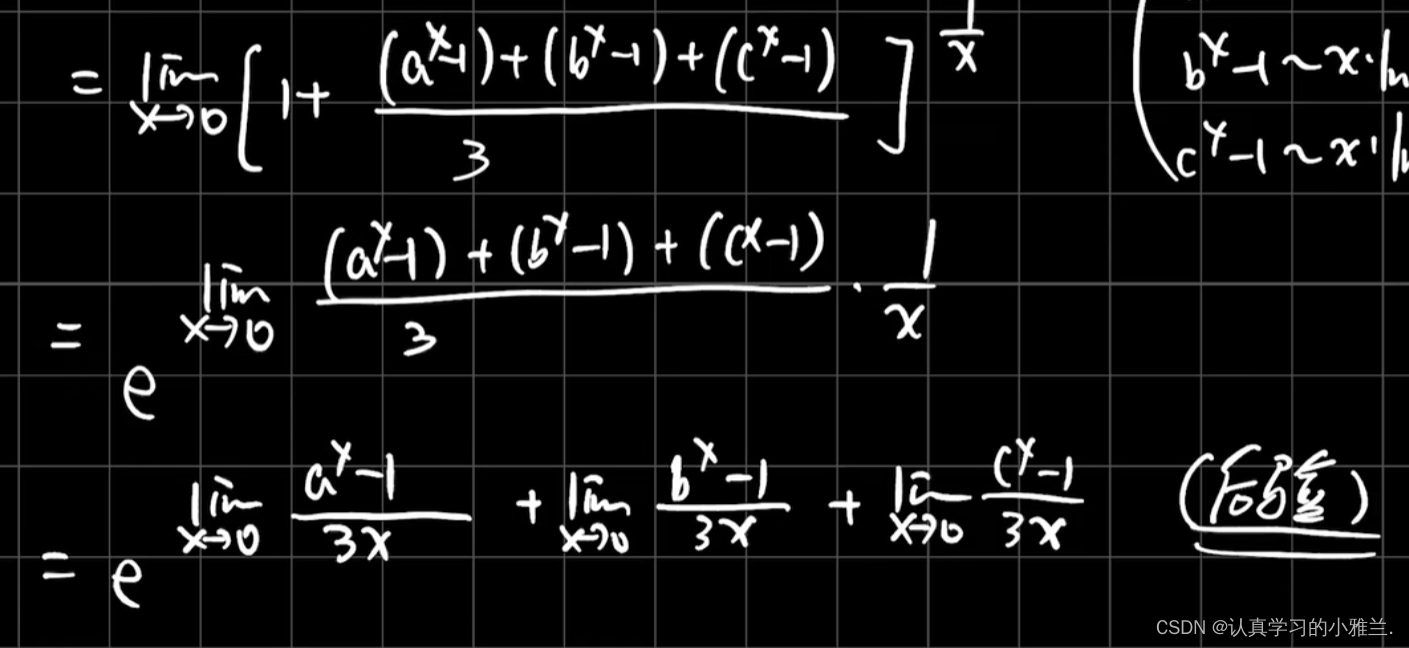有人可能会想：不是必须要求这三个极限存在才可以拆开吗？那不知道极限到底存不存在就把它拆开，这样做对吗？那么，这就是我们提及的后验问题啦，先拆开后，再看极限是否存在，如果不存在就返回反式，再来考虑别的方法，如果存在就最好不过了，继续往下做。这是一种常识。
考察无穷小比阶
采用倒代换
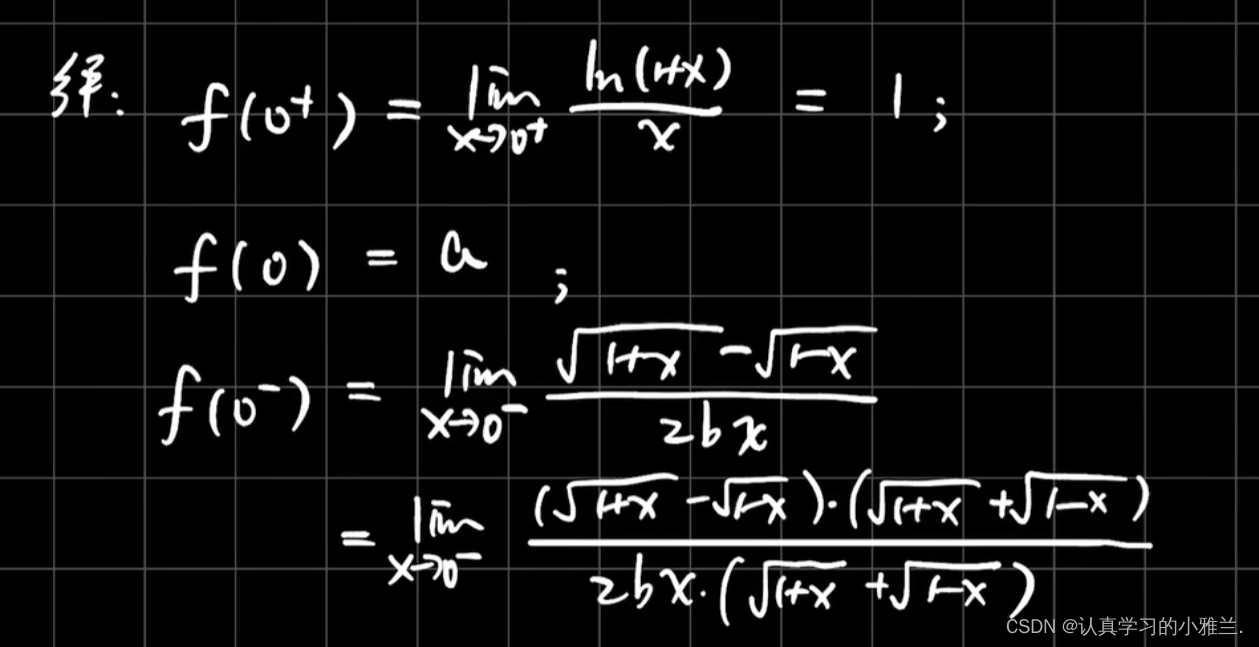采用的是分子有理化的方法
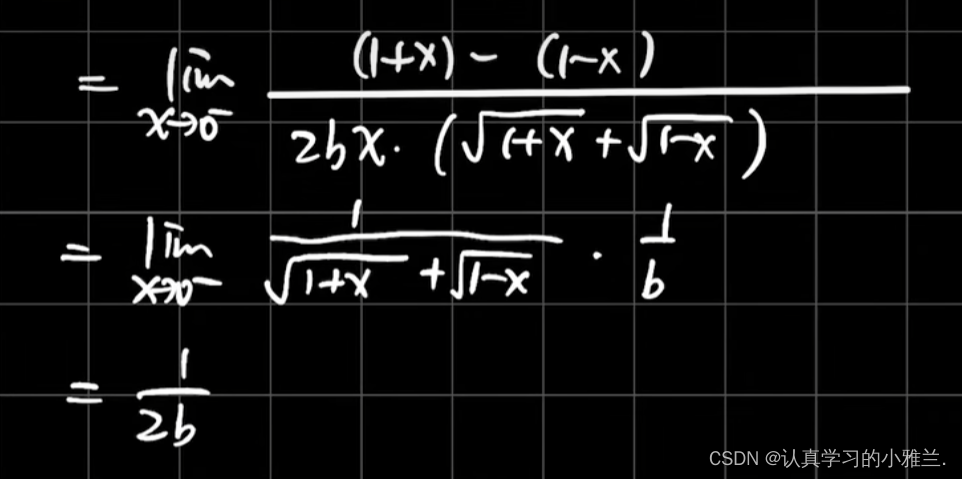
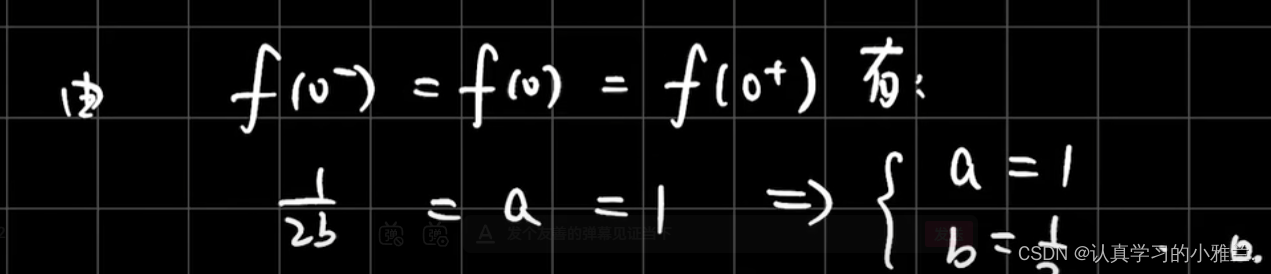
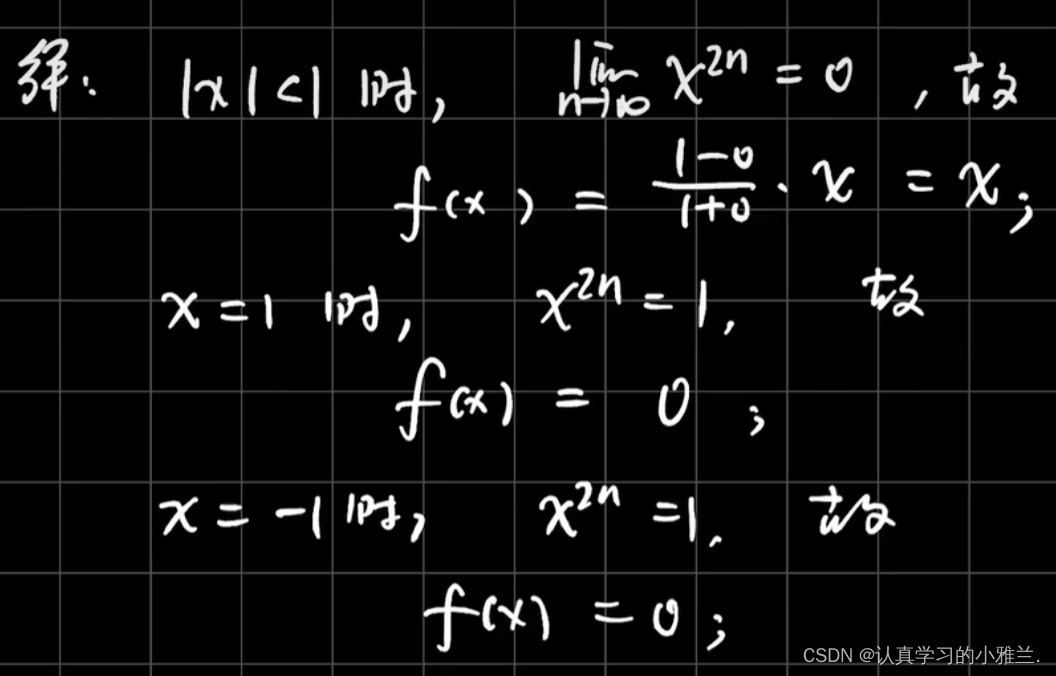
此函数没有水平渐近线
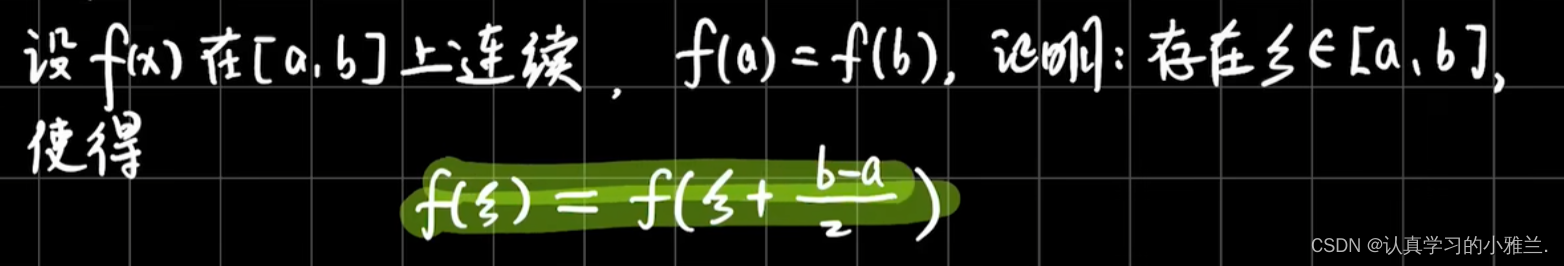
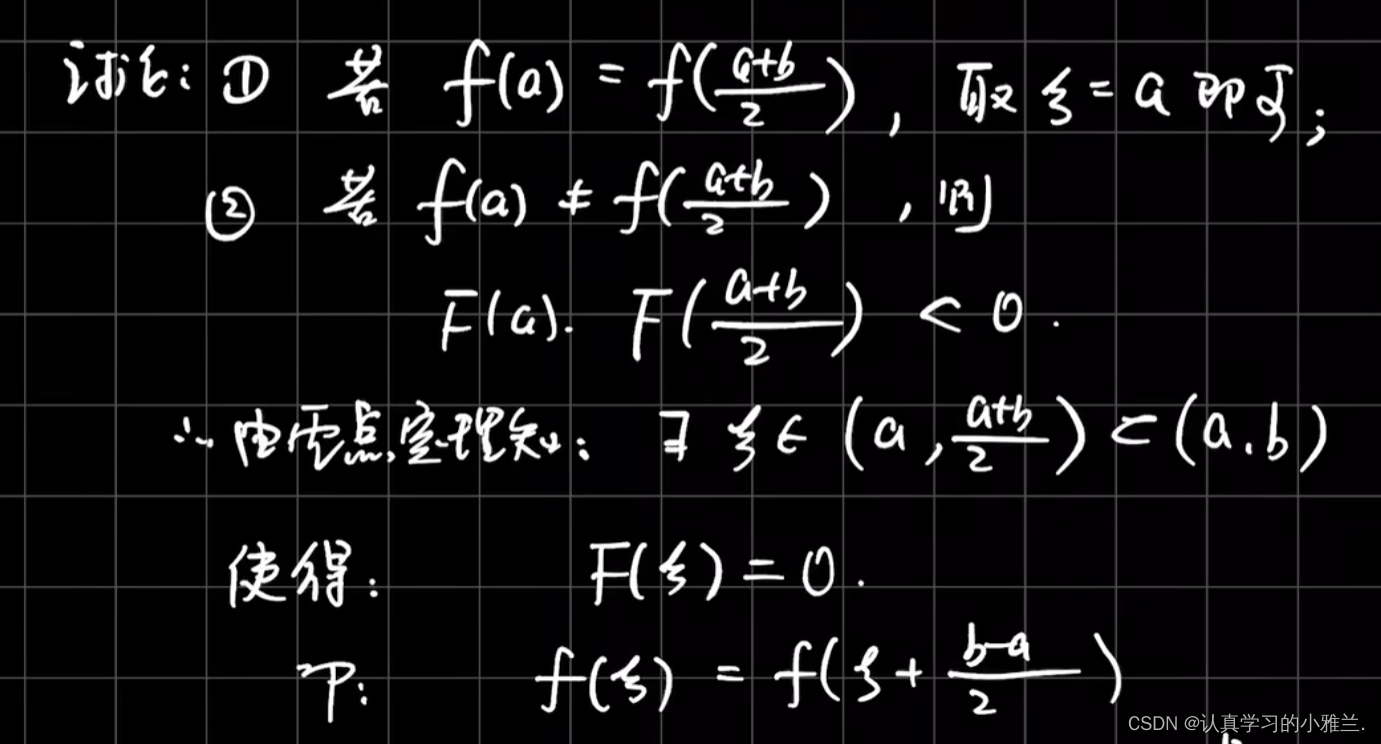好啦，我们的函数与极限的总复习就到这里结束啦
今天的内容有点小多噢，小雅兰花了好长的时间来学习，希望各位开学考的uu们跟随小雅兰的脚步一起，学习高等数学！！！（小雅兰的学校呢，开学开得非常之早，是为2月4号，我感觉全国的大学都没有我的学校开学开得早，至少在我所知道的，还没有哪个学校有我们这么早开学，呜呜呜，学不活了）虽然小雅兰知道自己已经学不完了，但还是一天一天坚持学习高等数学噢，除了高等数学之外，还有英语啊，计算机基础啊（考那些稀奇古怪的ppt word excel真是头疼得很） C语言啊 还有各种水课（什么思想道德与法治、大学心理健康教育......) 服辽服辽
