概述

对相机进行噪声模型分析，主要目的是为了更好地处理kincet深度图。
此外，噪声模型也可以更好地应用给kinectfusion系统pipeline中的滤波、体积融合以及位姿估计等动作。
实验结果表示，这样做的好处是可以重建更为精细的细节以及thinner surface。
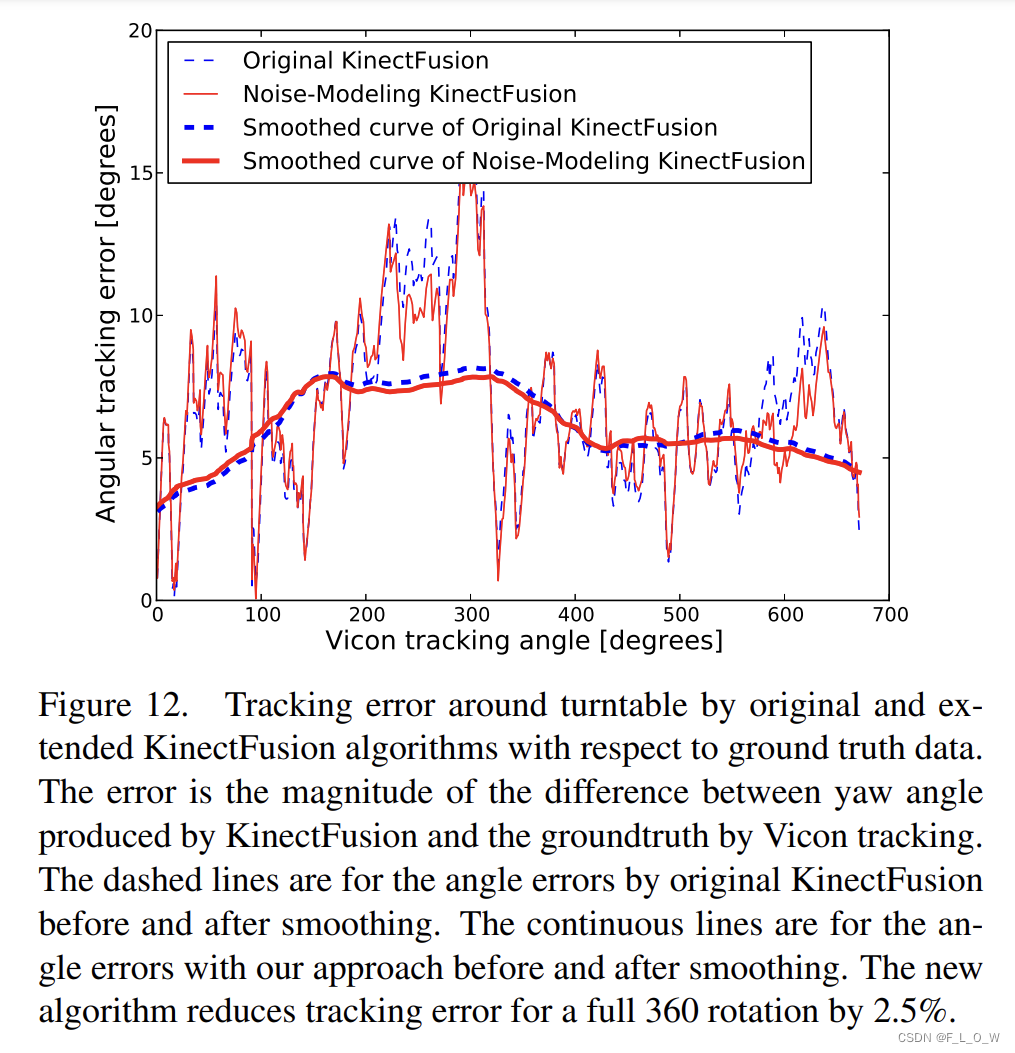
定量结果进一步地表明，噪声模型的引入，亦可以提高姿态估计的精度。

开源代码实现：https://github.com/intelligent-control-lab/Kinect_Smoothing/tree/master/kinect_smoothing （仅仅是给深度图去噪的部分有）
论文链接： http://users.cecs.anu.edu.au/~nguyen/papers/conferences/Nguyen2012-ModelingKinectSensorNoise.pdf

效果如何？

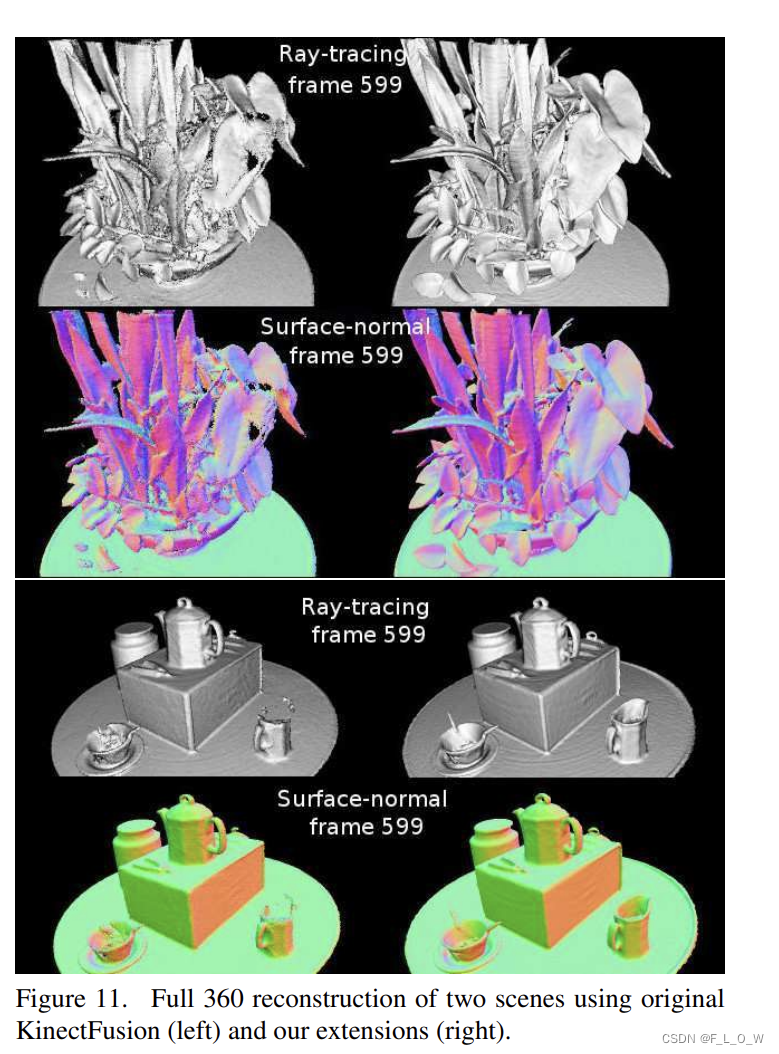
左边是原始结果，右边是引入噪声模型之后的结果：

初看只觉得提升了物体的完整性，倒是没太看出来对于细节的提升。

take home message

lateral noise 模型

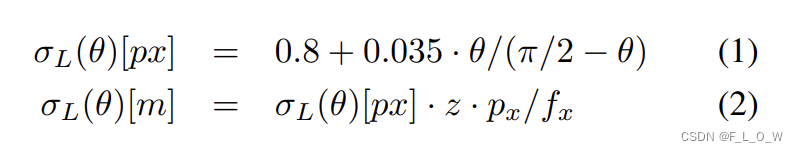
axial noise 模型

0-60°时：

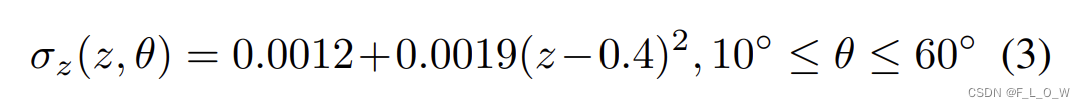
再考虑到 $\theta$接近于90°的情况，使用双曲线模型进行拟合，最终有：

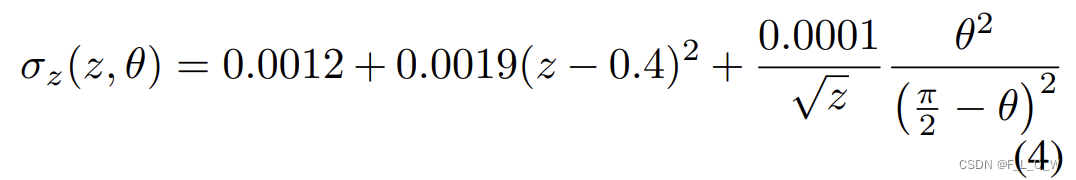
实验

kinect 传感器的噪声，在此我们直接定义为测量深度与实际深度之间的差别。

早些时候，轴向噪声（axial noise）是直接通过比较某一平面物体（比如说门）以及目标测量值（垂直于sensor的z轴）的平均深度而实现。
当sensor距离target越来越远的时候，深度测量值的方差数值呈现出上升的趋势。
但是没有去研究 surface angle或lateral noise。
lateral noise的测量没有那么直观，理想情况下是一种点扩散模型。
完全恢复这种点扩散模型是非常困难的。
一种可选的思路是用sensor的step response function进行近似。

---

简而言之：
approximate the PSF as the distribution of absolute distances from the observed edge pixels to a fitted straight edge of a planar target

实验设定

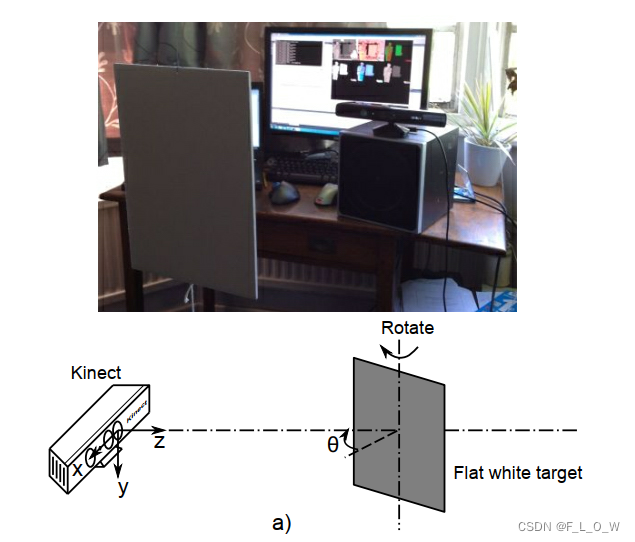
深度成像在0.4m到3.0m之间。

lateral noise与axial noise的定义

lateral noise从深度图的纵向边上进行提取：

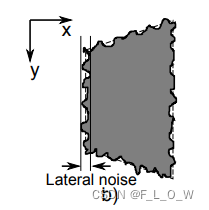
axial noise从raw depth与拟合的plane之间进行提取：

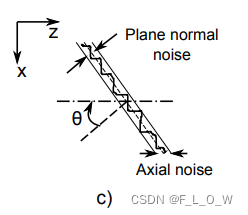
axial noise与lateral noise的提取

提取lateral noise与axial noise过程的示意图为：

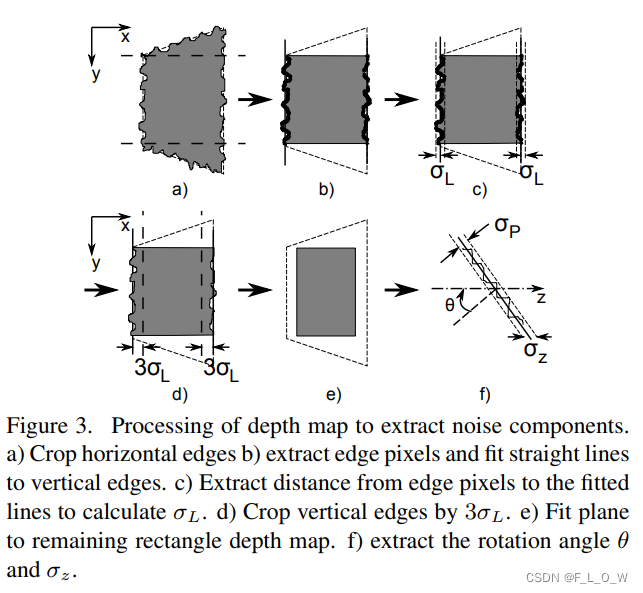
步骤(a)- 步骤（c）的目的是计算得到lateral noise STD ${\sigma }_L$:
（a） 裁剪出两条水平边；
（b）提取两条竖直边上的像素点，然后拟合成两条竖直线；
（c）提取边缘像素点到拟合直线的距离，并用于计算lateral noise STD ${\sigma }_L$；

---

（d）向内裁剪两个垂直边三倍${\sigma }_L$；
（e）拟合平面，使得其仍然保持为一个矩形的深度图；
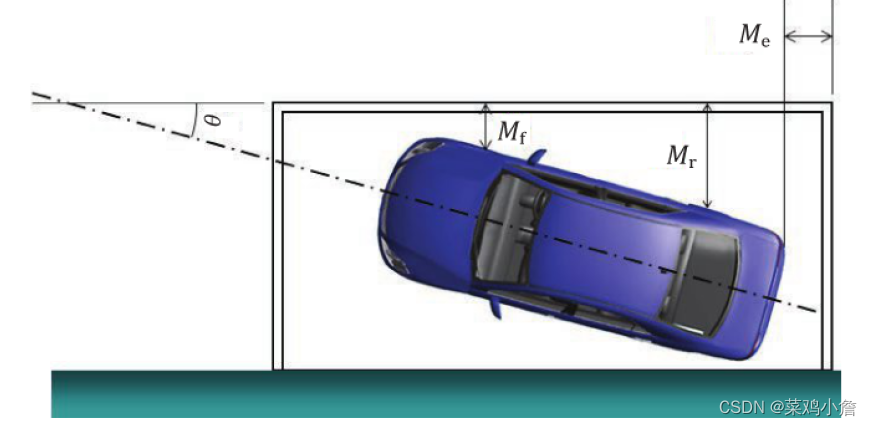
（f）提取旋转角度 $\theta$以及 ${\sigma }_Z$。

平面拟合可以通过使用orthogonal distance regression来实现。
下图为一些不同$z$位置和平面角度的示例：

噪声分布的结果和建模

target的大小是 $A2$ - $A5$。
距离从0.5m到2.75m，步距为0.25m。
在每个距离下，抓取了不同角度$\theta$的1000张深度图。这会导致在每个角度、每个距离都能够抓取大概10张左右的的深度图。
我们使用：
$A5$大小的平面在0.5m、0.75m，
$A4$大小的平面在1.0m、1.25m，
$A3$大小的平面在1.5m、1.75m，
$A2$大小的平面在2.25m、2.5m、2.75m。

---

使用kinect出厂时候的默认内参来进行镜头检校，fov是70°，等效焦距是585个像素，主点直接定义为图像中心。

三个样例距离的噪声分布有如：

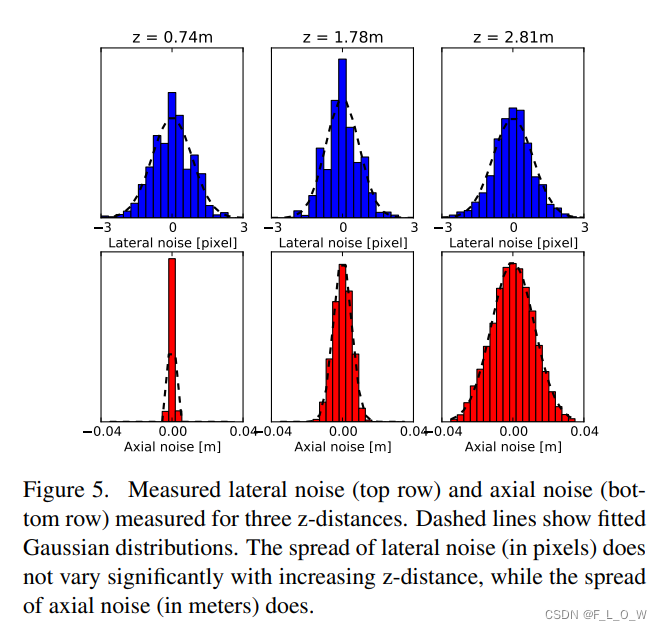
显然，lateral noise几乎不随着深度变化而显著变化。相比之下，axial noise随着深度的增加而显著增加。

图6则给出lateral noise和axial noise关于z轴距离更加直观的表现，注意，图表中避免了极限surface angle时的情况，因为无效深度像素会使得鲁棒的平面拟合不切实际：

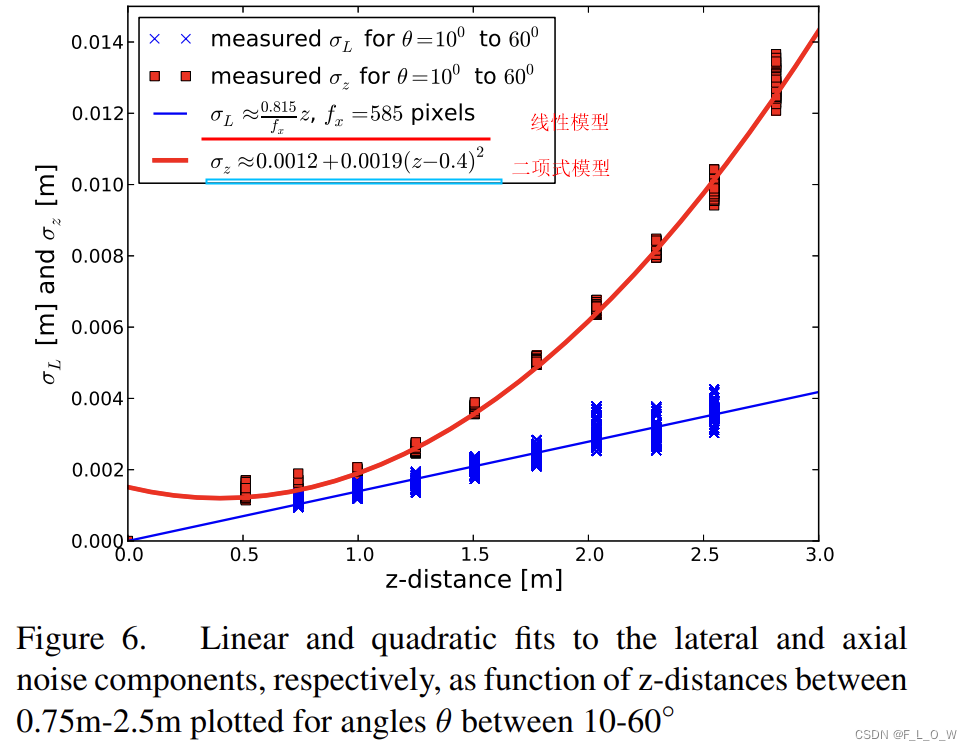
最终拟合得到的lateral noise模型

图7a展示了 lateral noise（单位是像素）关于距离和角度的变化情况：

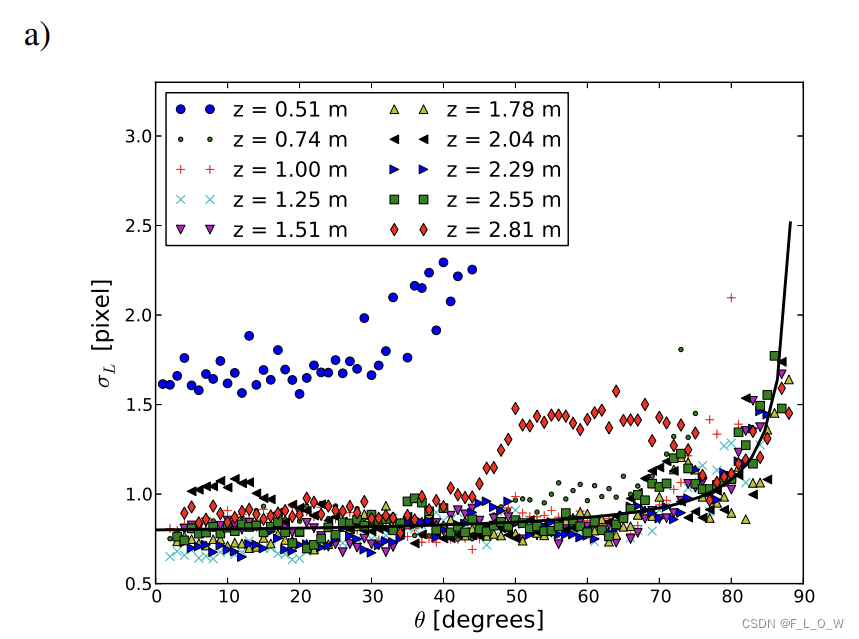
可以发现，

1. 除了在 $z=0.5m$的情况下，${\sigma }_L$在其他距离下的变化并不大；
2. 在 70°以前，${\sigma }_L$呈现微微上升的状态；如果将像素值转换成真实世界中的距离的话，就是图6中所呈现的线性增长情况。

去除小于0.5m以及大于2.8m距离的无效数据，利用常规最小二乘方法回归出线性模型（用于模拟常规接近于70°时的情况）与二次项模型（用于模拟接近于90°时的变化情况）的组合形态，正如上图（a）中黑色曲线所示。
lateral noise在像素和真实世界中的公式分别为：

最终拟合得到的axial noise模型

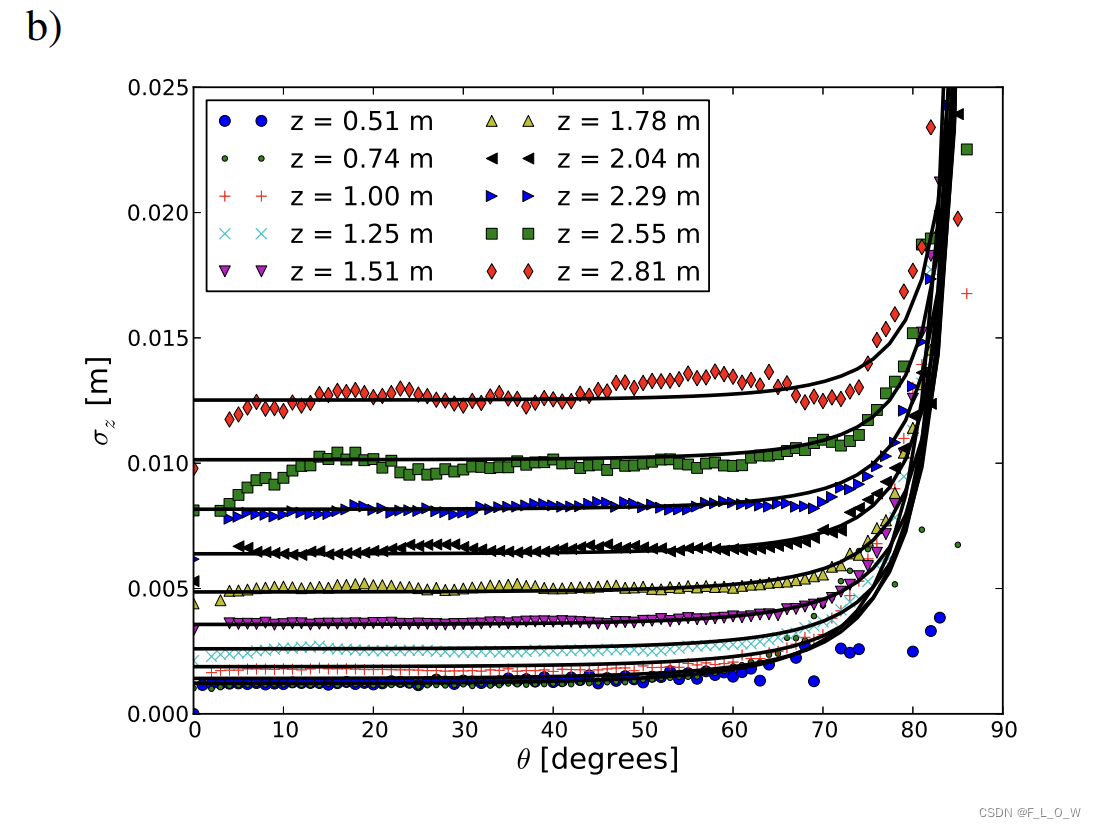
可以看到，

1. ${\sigma }_z$在不同的深度值的体现是非常不一样的，但是对于距离恒定，角度变化的情况下，60度以内基本恒定，90度以上就变得相对陡峭；
2. 当距离超过 2.5m的时候， ${\sigma }_z$在接近于0°的时候会体现较为显著的下降趋势。这主要是因为 Kinect的深度分辨率在远距离会有所下降。

---

假定在10°-60°之间 z轴向的噪声是恒定的，并使用线性回归来你和得到z轴向噪声与距离之间的关系。
当然，在线性回归的时候避免引入 10° - 60°以外的无效数据。

此时有：

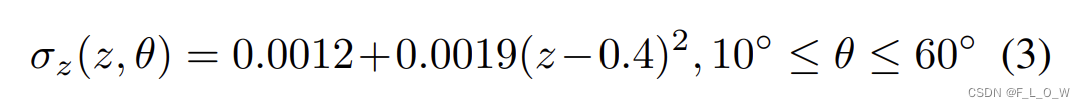
再考虑到 $\theta$接近于90°的情况，我们使用双曲线模型进行拟合，最终有：

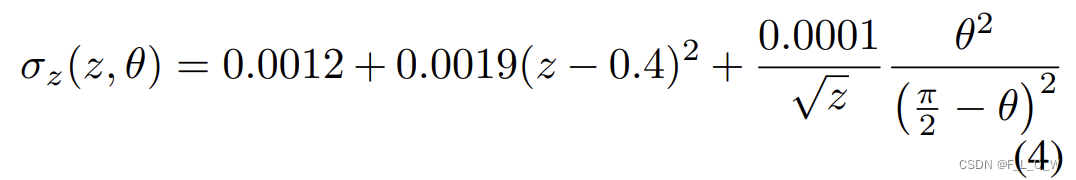
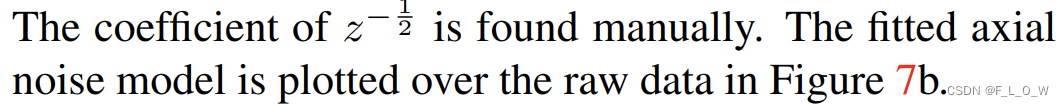
应用噪声模型至KinectFusion

在KinectFusion中，移动的深度相机的pose是通过传统ICP的point-plane变种而实现的。
Drift的减轻主要时通过frame-to-model来实现的。
隐式模型的提取主要有两种方式：ray-casting或marching cubes。

---

数学标识：

$\mathbf{u}=(x,y)$： 深度图上的2D像素坐标；
${\mathbf{D}}_i(\mathbf{u})$：在time frame $i$，$u$位置上的深度数值；
$\mathbf{K}$：内参矩阵
${\mathbf{v}}_i(\mathbf{u})={\mathbf{D}}_i(\mathbf{u}){\mathbf{K}}^{-1}[\mathbf{u},1]$：对应于深度 $\mathbf{u}$的三维顶点；
${\mathbf{v}}_i^g={\mathbf{T}}_i{\mathbf{v}}_i$： 全局坐标系下的顶点。

数据滤波

一种在3D空间下对Kinect 数据滤波的方式是将噪声PDF建模成 $3\ast 3$的协方差矩阵。
但lateral nosie与深度无关，这会导致协方差矩阵有所冗余。
进而，我们可以直接在二维的深度图上继续进行滤波。

注意，PDF仅仅在Z方向上expand。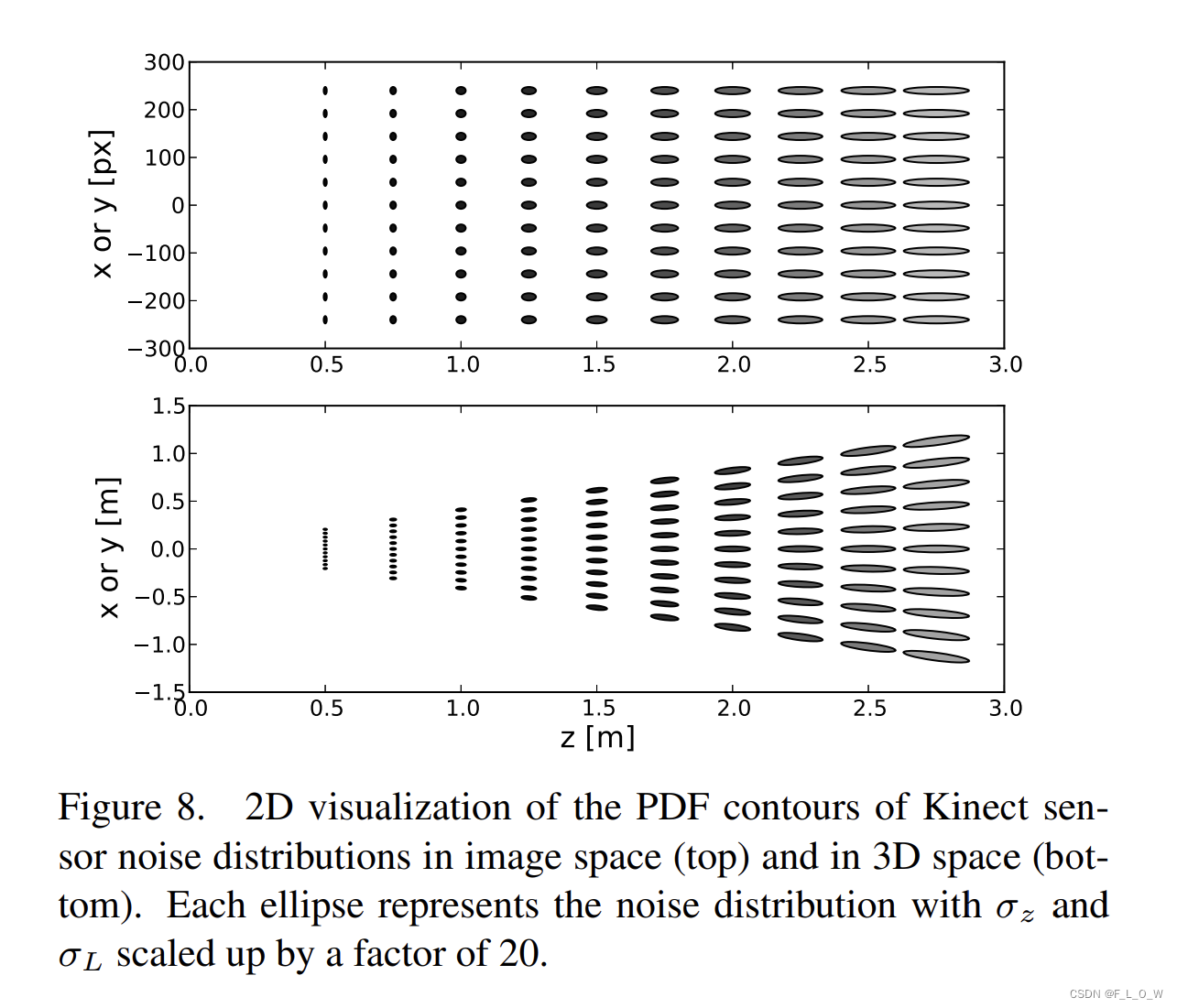

换言之， ${\sigma }_L$和${\sigma }_Z$可以被直接用于做深度图的保边滤波【怎么理解保边？】。
${\sigma }_L$在多数情况下会小于1。
首先使用$3\ast 3$大小的核对深度图 ${\mathbf{D}}_i$进行平滑滤波，进而得到平滑后的深度图 $\widetilde{{\mathbf{D}}_i}(\mathbf{u})$。

实现代码为：

	def modeling_filter(self,img, theta=30, threshold=10, depth_min=100, depth_max=4000,noise_type='normal'):
		"""
		modeling the noise distribution and filtering based on noise model
		:param img: numpy-array,
		:param theta: float, average angle between kinect z-axis and object plane.
		:param threshold: int, thrshold for 'modeling' and 'modeling_pf' method.
		:param depth_min: float,  minimum valid depth, we only filter the area of depth > depth_min
		:param depth_max: float,  maximum valid depth, we only filter the area of depth < depth_max
		:param noise_type: 'normal' of 'pf',
				'normal': noise modeling based on 'Modeling Kinect Sensor Noise for Improved 3D Reconstruction and Tracking'
				'pf': noise modeling based on 'Kinect v2 for Mobile Robot Navigation: Evaluation and Modeling'
		:return: denoised img: numpy-array
		"""

		denoised_img = img.copy()
		h, w = img.shape
		lateral_noise = self._lateral_noise_pf if noise_type=='pf' else self._lateral_noise
		axial_noise = self._axial_noise_pf if noise_type == 'pf' else self._axial_noise
		l_noise = np.power(lateral_noise(img, theta), 2)
		z_noise = np.power(axial_noise(img, theta), 2)
		distance_metrics = np.array([[1.414, 1, 1.414],
		                             [1, 0, 1],
		                             [1.414, 1, 1.414]])
		for x in range(h):
			for y in range(w):
				D_u = img[x, y]
				if D_u >= depth_min and D_u <= depth_max:
					# 计算 sigma_l, sigma_l
					sigmal_l = l_noise[x, y]
					sigmal_z = z_noise[x, y]
					D_k = img[max(x - 1, 0):x + 2, max(y - 1, 0):y + 2]
					delta_z = abs(D_k - D_u)
					delta_u = distance_metrics[int(x == 0):2 + int(x < h - 1), int(y == 0):2 + int(y < w - 1)]
					mark = delta_z < threshold
					D_k_list = D_k[mark].flatten()
					u_list = delta_u[mark].flatten()
					z_list = delta_z[mark].flatten()
					if len(D_k_list) > 0:
						w_k_list = np.exp(- u_list ** 2 / (2 * sigmal_l) - z_list ** 2 / (2 * sigmal_z))
						denoised_img[x, y] = np.sum(D_k_list * w_k_list) / w_k_list.sum()
		return denoised_img

从平滑后的深度图中，我们可以引出得到法向量图：

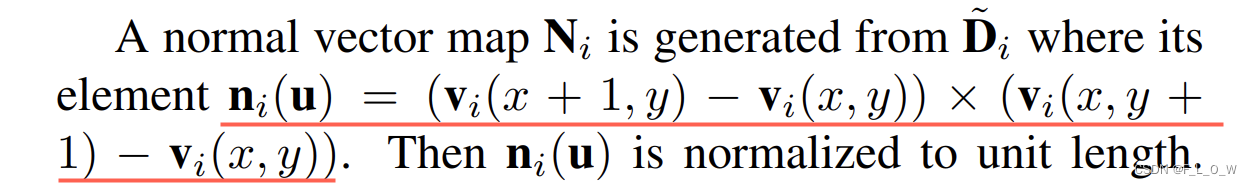
所谓的surface angle也就是 法向量方向与相机z轴方向之间的夹角，即：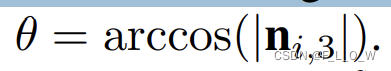

位姿估计： 加权ICP

数据关联的方式为：projective data association。
在数据关联的过程中，不仅仅使用了距离以及法向的阈值，还限制了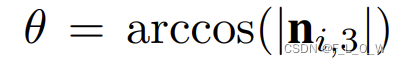
需要小于 70°。

point-plane 能量函数线性化的前提假设是上一个pose到下一个pose之间的移动是非常小的。
这种方式会使得每一个数据都有着一样的重要程度，可能会导致次优解。
因此，这里引入加权的概念，即有：

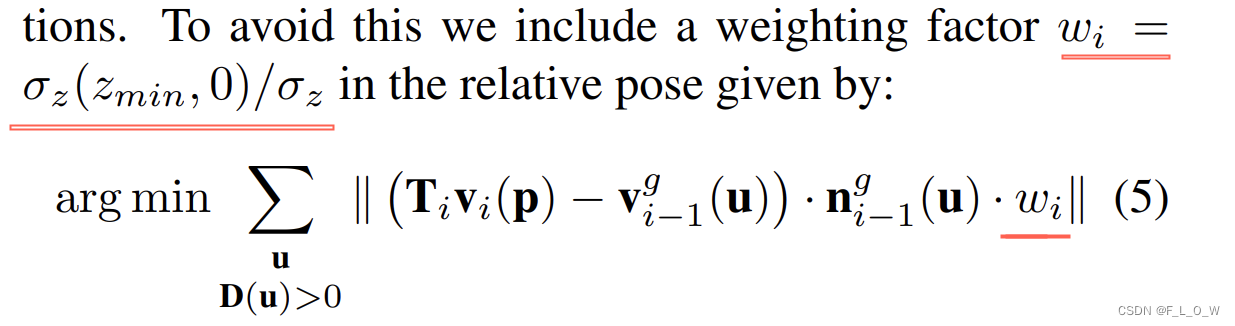
Volumetric depth map fusion

为了更好地适应高斯形态的axial-noise，进一步提出在voxel grid中的tsdf编码，主要是基于axial noise pdf的cdf。

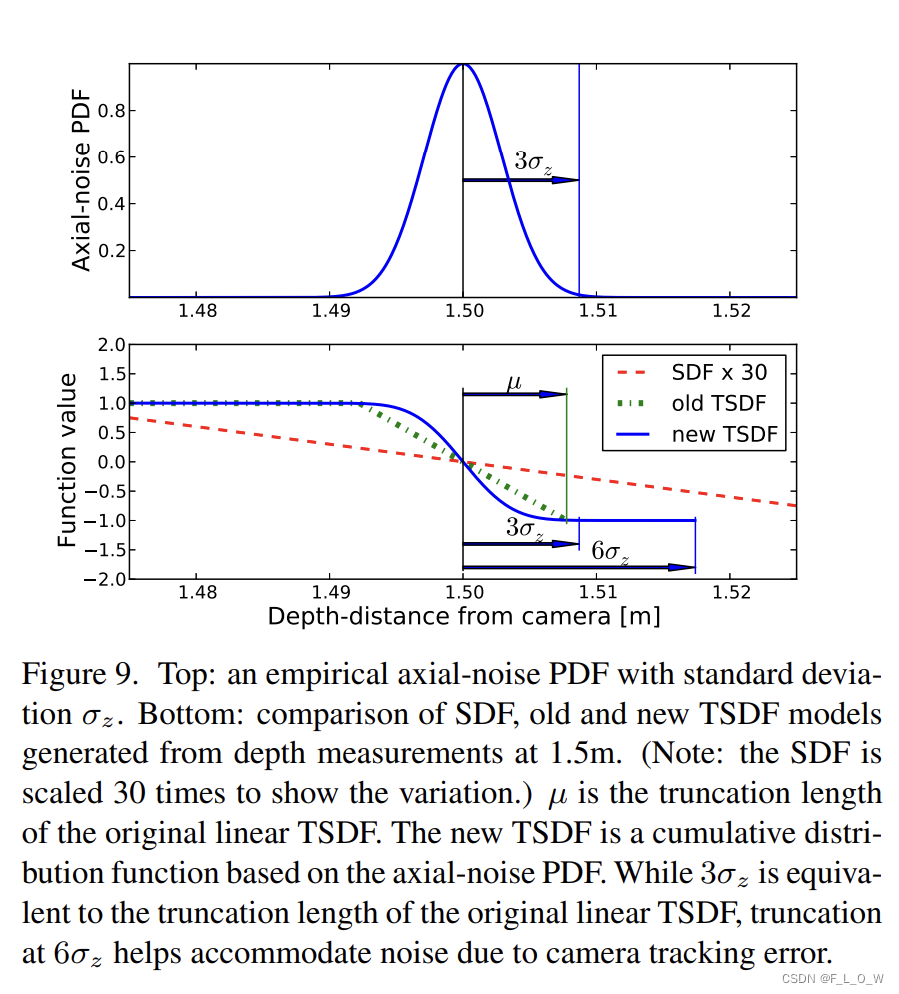
在最原始的sdf中， truncation length $\mu$主要用于去评估不确定性。在此，我们直接将其设置为 $3{\sigma }_z$。

在实验中，当截断长度为 $6{\sigma }_z$的时候，可以进一步地包容住相机tracking的误差。

随着ICP误差的逐步减小，truncation length可以被自适应地从 $6{\sigma }_z$降低至$3{\sigma }_z$。

这个过程的伪代码是：

上述伪代码的第17行是一个近似的高斯CDF的修改版本，可以使得产生的数值在 [-1,1]之间。
而 $sd{f}_k$则指代原本KinectFusion算法中的sdf数值。
在原始的KinectFusion系统中，如果下一帧融合进来的点云距离表面比较远（比如说噪声），却会以同样的权重intergrate进来，就会导致几何特征有所丢失。

为了避免这个问题，标准化的项会被加进voxel weight中，如上述伪代码的第18行所示。其中，指数项就是noise distribution weight。
项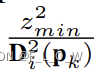主要用来自适应 3D noise 分布的宽度，在深度增加的情况下尽量覆盖更多的voxels。
项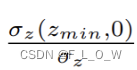 accounts for increased length of the distribution for larger z-depths:

重建与tracking结果

代码分析

初始化

从去噪滤波初始化的“flag”可以看出来，设计了四种方式：“modeling”、“modeling_pf”、“anisotropic”、“gaussian”。
我们主要关注“modeling”的方式： 使用kinect v2 噪声模型进行滤波，‘Modeling Kinect Sensor Noise for Improved 3D Reconstruction and Tracking’。，需要指定的参数为：

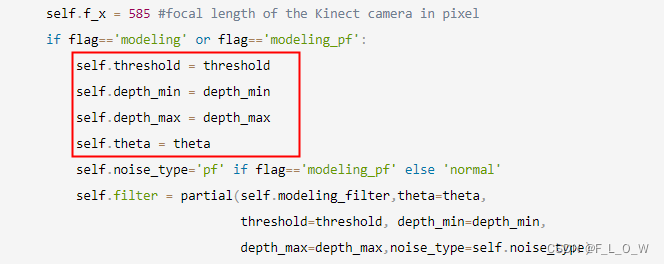
class Denoising_Filter(object):
	"""
	Denoising filter can be used to improve the resolution of the depth image
	"""
	def __init__(self, flag='modeling',theta=30, threshold=10,depth_min=100,depth_max=4000,
	             ksize=5, sigma=0.1,niter=1,kappa=50,gamma=1,option=1):
		"""
		:param flag: string, specific methods for denoising.
				'modeling': filter with Kinect V2 noise model,  'Modeling Kinect Sensor Noise for Improved 3D Reconstruction and Tracking'
				'modeling_pf': another Kinect V2 noise modeling by Peter Fankhauser, 'Kinect v2 for Mobile Robot Navigation: Evaluation and Modeling'
				'anisotropic': smoothing with anisotropic filtering, 'Scale-space and edge detection using anisotropic diffusion'
				'gaussian': smoothing with Gaussian filtering
		:param theta: float, the average angle between Kinect z-axis and the object plane.
				Used to calculate noise in the 'modeling'  and 'modeling_pf' method
		:param threshold: int, thrshold for 'modeling' and 'modeling_pf' method.
		:param depth_min: float,  minimum valid depth, we only filter the area of depth > depth_min
		:param depth_max: float,  maximum valid depth, we only filter the area of depth < depth_max
		:param ksize: int, Gaussian kernel size
		:param sigma: float, Gaussian kernel standard deviation
		:param niter: int, number of iterations for anisotropic filtering
		:param kappa: int, conduction coefficient for anisotropic filtering, 20-100 ?
		:param gamma: float, max value of .25 for stability
		:param option: 1 or 2, options for anisotropic filtering
				1: Perona Malik diffusion equation No. 1
		        2: Perona Malik diffusion equation No. 2
		"""
		self.flag=flag
		self.f_x = 585 #focal length of the Kinect camera in pixel
		if flag=='modeling' or flag=='modeling_pf':
			self.threshold = threshold
			self.depth_min = depth_min
			self.depth_max = depth_max
			self.theta = theta
			self.noise_type='pf' if flag=='modeling_pf' else 'normal'
			self.filter = partial(self.modeling_filter,theta=theta,
			                      threshold=threshold, depth_min=depth_min,
			                      depth_max=depth_max,noise_type=self.noise_type)
		elif flag=='gaussian':
			self.ksize = ksize
			self.sigma = sigma
			self.filter = partial(cv2.GaussianBlur,ksize=(ksize,ksize),sigmaX=0)
		elif flag=='anisotropic':
			self.niter = niter
			self.kappa = kappa
			self.gamma=gamma
			self.sigma=sigma
			self.option=option
			self.filter = partial(self.anisotropic_filter,niter=niter,kappa=kappa,
			                      gamma=gamma,sigma=sigma)

		if flag not in self.all_flags:
			raise('invalid  flags. Only support:', self.all_flags)

结论