声明：文章是从本人公众号中复制而来，因此，想最新最快了解各类算法的家人，可关注我的VX公众号：python算法小当家，不定期会有很多免费代码分享~

前沿创新 | KAN模型及其组合模型回归预测应用，Python预测回归全家桶更新

KAN一种全新的神经网络架构，与传统的 MLP 架构截然不同，且能用更少的参数在数学、物理问题上取得更高精度。本期将推出KAN及其组合模型（TCN-KAN、LSTM-KAN、Transformer-KAN、ResNet-KAN等等等）实现回归预测。KAN是2024年的最新研究成果，一经问世便受到众多关注，当前引用还比较少，早用早发文！！！

代码及参考文献获取见文末

KAN原理介绍

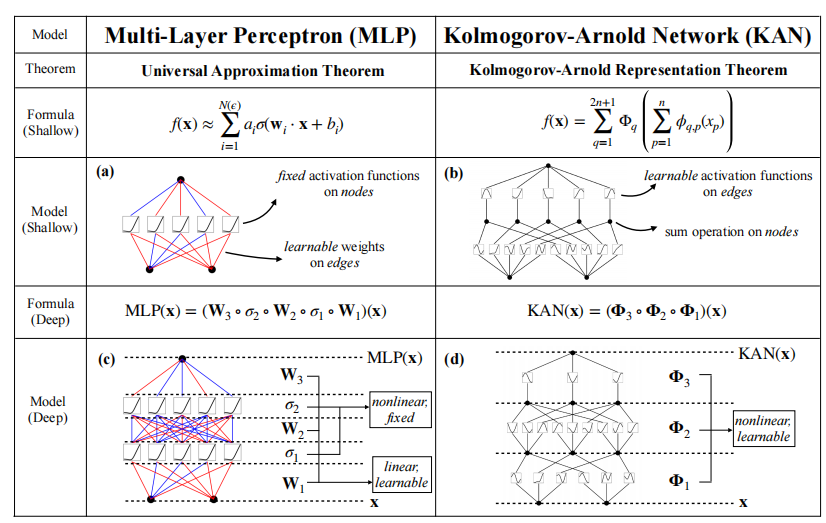
KAN网络架构是近期非常热门的一个模型，受到Kolmogorov-Arnold 定理的启发，任何连续的多变量函数 (f(x)) 都可以表示为一系列一维函数的组合。公式如下：

$$f(x)=\sum _{q=1}^{2n+1}{\Phi }_q\left(\sum _{p=1}^n{\phi }_{qp}(x_p)\right)$$

• ${\phi }_{qp}$和 ${\Phi }_q$ 是一维的可学习函数。
• 外层函数 ${\Phi }_q$ 作用于内层函数${\phi }_{qp}$ 的求和结果上。

这种表示形式允许 KAN 网络通过学习这些一维函数来逼近复杂的多变量函数，实现更灵活和强大的函数逼近能力。

MLP VS KAN

激活函数位置和类型:

• MLP中的激活函数是固定的，并且位于节点上。
• KAN中的激活函数是可学习的，并且位于边上。

模型结构:

• MLP依靠多层线性变换和固定的非线性激活函数来逼近函数。
• KAN通过可学习的非线性变换和节点上的求和操作来表示函数。
  这种比较展示了MLP和KAN在结构和功能上的关键差异，表明KAN通过更灵活和可学习的激活函数，提供了一种更强大的函数表示能力。

实验展示

本期推出KAN、KAN组合网络共10个模型，将会同步更新到Python回归预测全家桶中。下面进行展示部分模型的实验结果，输入数据为共享单车数据集。

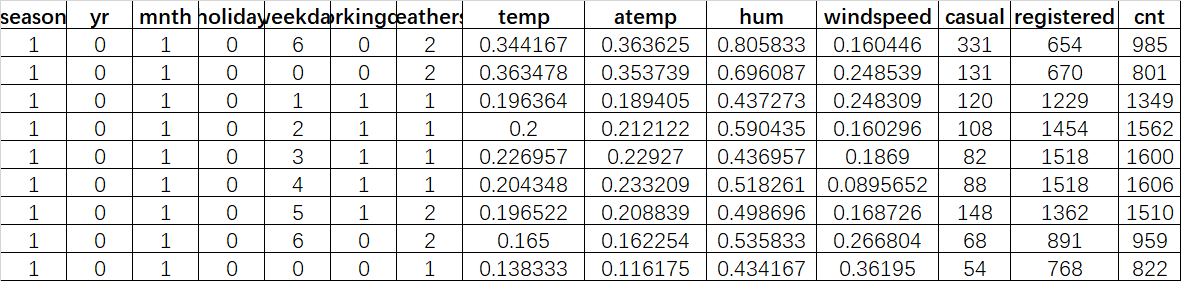
1、KAN

2、LSTM-KAN

3、BiLSTM-KAN

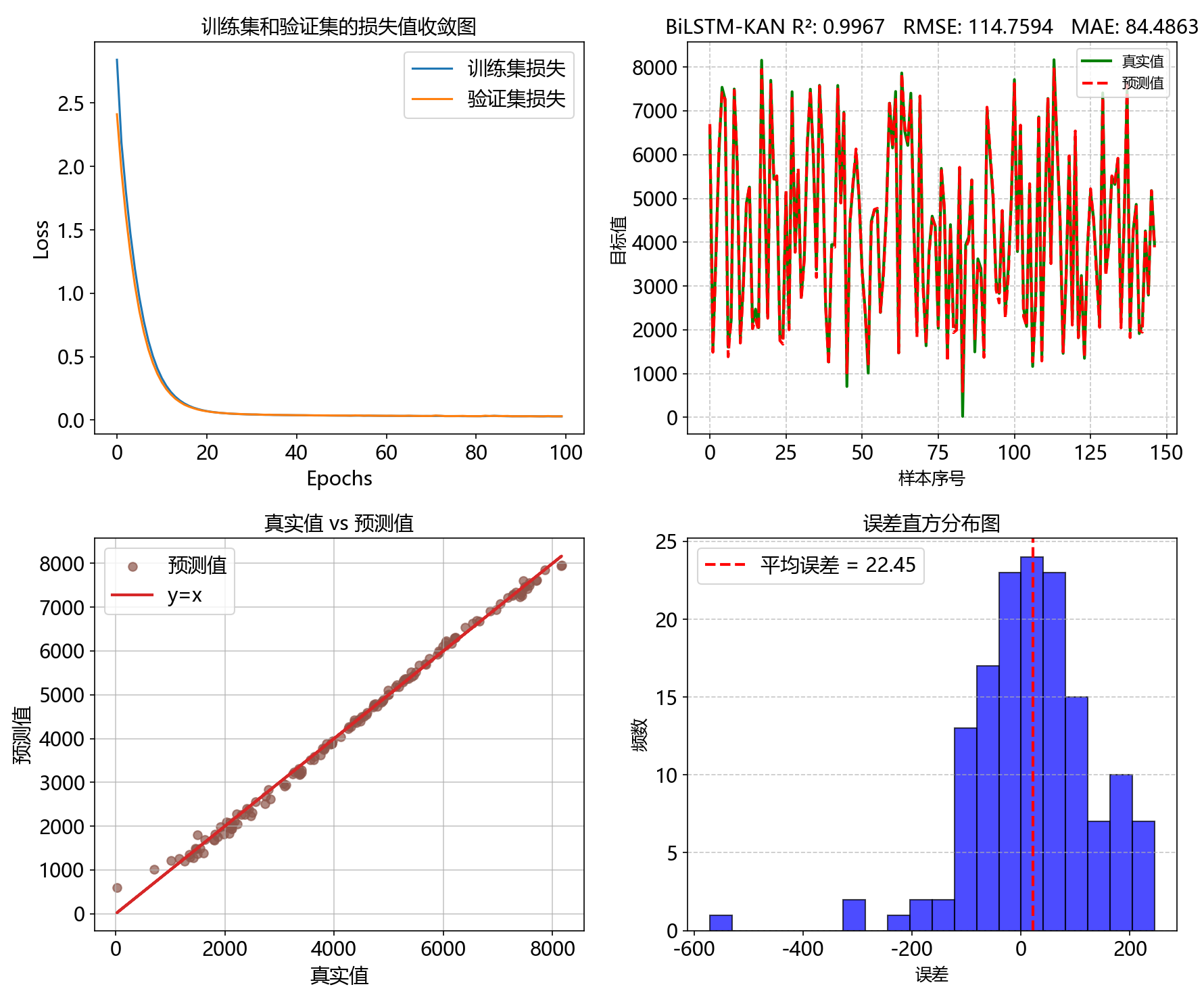
4、BiGRU-KAN

5、Attention-KAN

6、Transformer-KAN

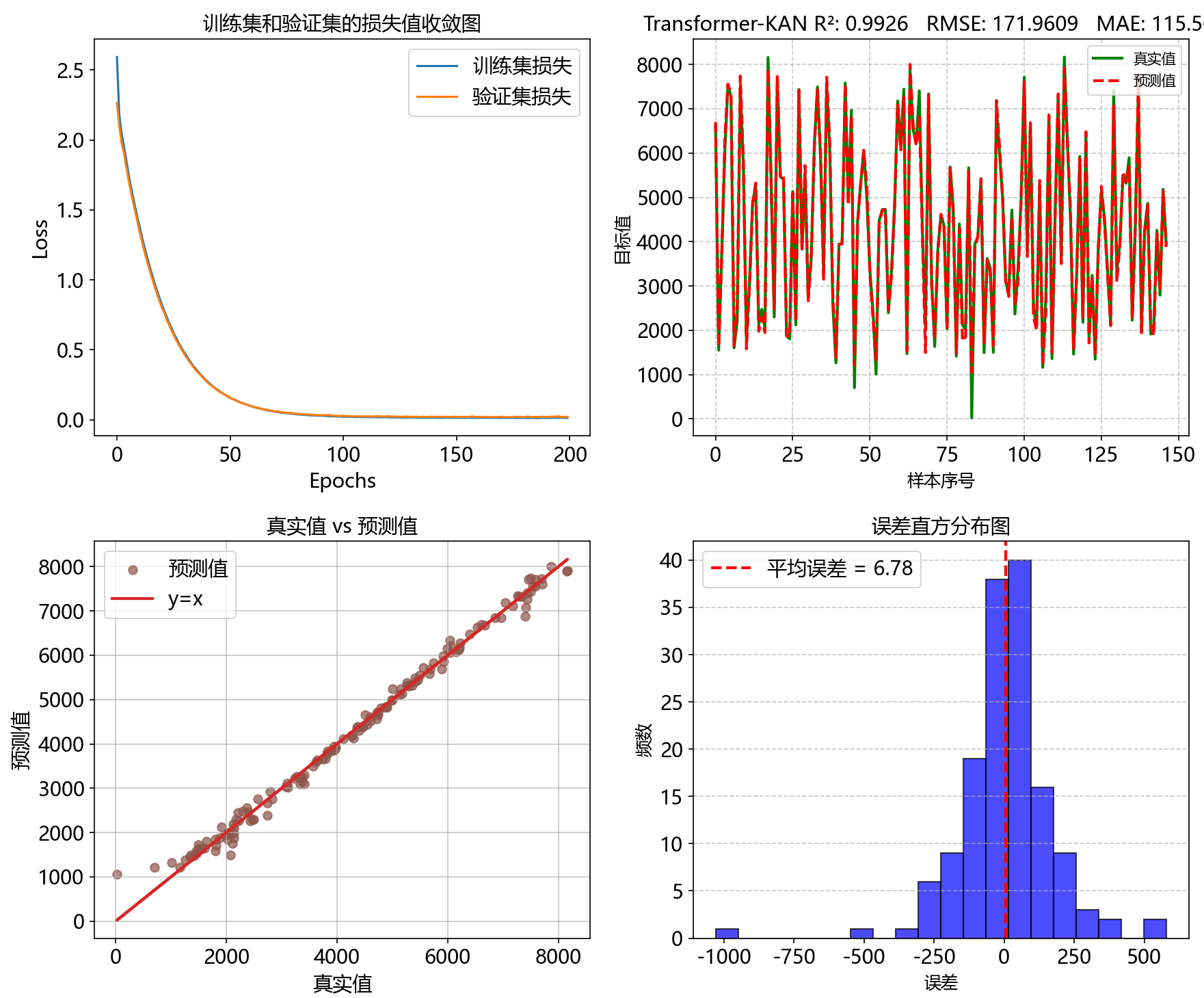
代码获取

代码获取

关注VX公众号 Python算法小当家 回复关键词 KAN