树与图的深度优先遍历
定义
从图的某个顶点出发,沿着一条路径尽可能深地访问图中顶点。
运用情况
- 图的连通性判断。
- 寻找特定路径或回路。
注意事项
- 要标记已访问的节点,以避免重复访问导致死循环。
- 对于有向图和无向图可能需要不同的处理。
解题思路
- 也是可以用递归方法,从起始顶点开始,访问该顶点,标记为已访问,然后对其未访问的邻接顶点进行深度优先遍历。
例如,对于一棵树,从根节点开始深度优先遍历,先访问根节点,再递归访问左子树和右子树。在图中,比如从一个顶点出发,访问相邻顶点,再递归深入访问它们的相邻顶点,直到无法继续深入为止,然后回溯。
AcWing.846树的重心
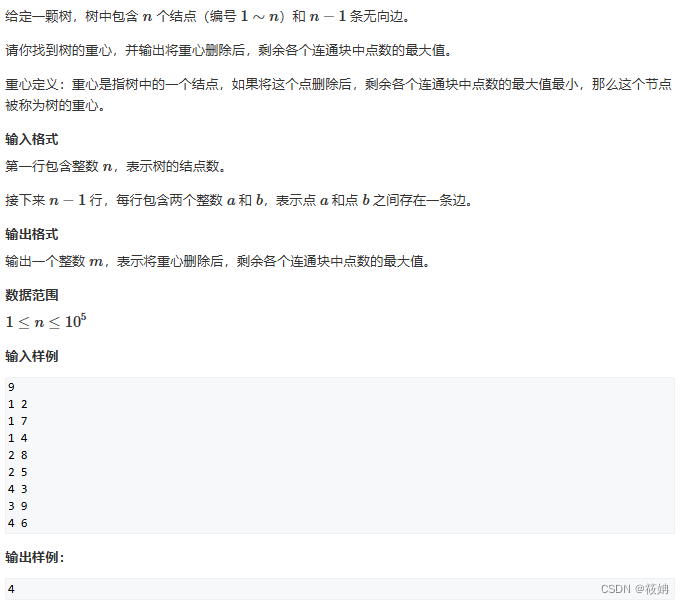
题目描述
846. 树的重心 - AcWing题库
运行代码
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int MAXN = 100005;
int n, root, ans, maxChild;
vector<int> G[MAXN];
int dfs1(int u, int fa) {
int size = 1;
for (int v : G[u]) {
if (v != fa) {
size += dfs1(v, u);
}
}
return size;
}
int dfs2(int u, int fa, int tot) {
int size = 1, maxSubtree = 0;
for (int v : G[u]) {
if (v != fa) {
int subtreeSize = dfs2(v, u, tot);
maxSubtree = max(maxSubtree, subtreeSize);
size += subtreeSize;
}
}
maxSubtree = max(maxSubtree, tot - size);
ans = min(ans, maxSubtree);
return size;
}
int main() {
cin >> n;
for (int i = 1; i < n; ++i) {
int u, v;
cin >> u >> v;
G[u].push_back(v);
G[v].push_back(u);
}
ans = n;
dfs1(root = 1, 0);
dfs2(root, 0, n);
cout << ans << endl;
return 0;
}代码思路
找到一棵树的重心,并输出删除重心后,剩余各个连通块中点数的最大值。代码采用了两次深度优先搜索(DFS)的策略来实现这一目标。
-
dfs1:第一次DFS是为了计算每个节点的子树大小(节点数)。从根节点开始,递归遍历每个子节点,并将子树的节点数累加到当前节点的子树大小中。
-
dfs2:第二次DFS是为了确定删除每个节点后,剩余树的最大连通块大小。这次DFS不仅递归遍历每个子节点,还计算以当前节点为根的子树被删除后,剩余部分的最大连通块大小,并更新全局变量
ans为所有可能情况中的最小值。 -
主函数:首先读取树的节点数
n,然后建立无向图的邻接表表示。之后,从节点1开始进行两次DFS,最后输出ans作为删除重心后,剩余连通块中点数的最大值。
改进思路
-
初始化根节点:原代码中直接将
root设为1,实际上在处理任意树结构时,可以选择任一节点作为起点,但最好明确指出这一点或者实现一个方法来自动选择一个合适的起点(如度最小的节点)。 -
减少全局变量使用:尽量减少全局变量的使用,可以将
ans和G作为参数传递给函数,提高代码的封装性和可重用性。 -
优化输出逻辑:在
dfs2中直接记录并更新最小的最大连通块大小,避免不必要的全局变量更新。
改进代码(AI生成)
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int MAXN = 100005;
vector<int> G[MAXN];
pair<int, int> findCentroid(int u, int fa, int tot, vector<int>& subtreeSize) {
int size = 1, maxSubtree = 0;
for (int v : G[u]) {
if (v != fa) {
auto [subtreeSz, _] = findCentroid(v, u, tot, subtreeSize);
size += subtreeSz;
maxSubtree = max(maxSubtree, subtreeSz);
}
}
maxSubtree = max(maxSubtree, tot - size);
subtreeSize[u] = size;
return {size, maxSubtree};
}
int main() {
int n;
cin >> n;
for (int i = 1; i < n; ++i) {
int u, v;
cin >> u >> v;
G[u].push_back(v);
G[v].push_back(u);
}
vector<int> subtreeSize(n + 1, 0);
auto [_, ans] = findCentroid(1, 0, n, subtreeSize);
cout << ans << endl;
return 0;
}其它代码
#include<iostream>
#include<cstring>
using namespace std;
const int N=100010;
int h[N],e[N*2],ne[N*2],idx,ans=N;
bool st[N];
int n;
void add(int a,int b)
{
e[idx]=b;ne[idx]=h[a],h[a]=idx++;
}
int dfs(int u)
{
st[u]=true;
int size=0,sum=0;
for(int i=h[u];i!=-1;i=ne[i])
{
int j=e[i];
if(st[j]) continue;
int s=dfs(j);
size=max(size,s);
sum+=s;
}
size=max(size,n-sum-1);
ans=min(ans,size);
return sum+1;
}
int main()
{
memset(h, -1, sizeof h);
cin>>n;
for(int i=0;i<n-1;i++)
{
int a,b;cin>>a>>b;
add(a,b),add(b,a);
}
dfs(1);
cout<<ans<<endl;
return 0;
}代码思路
数据结构与初始化
- 使用邻接表表示无向树结构。h[N]数组用于存储每个节点的边链表的头指针,初始值为-1;e[N*2]和ne[N*2]分别存储边的目标节点和下一条边的索引,idx用来追踪当前使用的边索引;st[N]数组标记节点是否已被访问过。
- N定义为节点数的上限,初始化为100010。
- 全局变量ans初始化为N,用于记录删除某个节点后,剩余各个连通块中点数的最大值,初始化为一个较大的值以便后续更新。
函数定义
add(int a, int b)函数用于添加边,构建无向图。参数a和b分别代表连接的两个节点。
主要逻辑
- 读取输入:读取节点数n,然后读取n-1条边的连接关系,构造无向树。
- 深度优先搜索(DFS):定义dfs(int u)函数,用于递归地遍历以节点u为根的子树,并计算以下内容:遍历子树中的每个节点,跳过已访问的节点。
- 计算每个子树的节点数(大小),并记录当前子树的最大节点数size。
- 计算以当前节点为根的子树的节点总和sum。
- 更新最大连通块的大小,考虑当前节点作为分割点时的情况,即size=max(size, n-sum-1),其中n-sum-1表示除了当前子树以外的其他节点数。
- 返回当前子树的节点数加1(包括根节点自己)。
- 寻找重心并输出结果:从根节点(这里假设为节点1)开始调用dfs函数。遍历结束后,ans中存储的就是删除任一节点后,剩余各个连通块中点数的最大值。最后输出ans。
优化与注意事项
- 代码中通过双向连边构建无向图,但在树结构中,实际上只需要单向连边即可,不过这不影响算法的正确性。
- 该算法通过一次深度优先遍历完成任务,时间复杂度为O(n),是较为高效的解法。
- 代码中没有显式地寻找并标识重心,而是直接计算并输出了删除任一节点后最不利情况下的连通块大小,这在逻辑上等效于找到重心的概念,但并未直接指出哪个节点是重心。