每日一题——8行Python代码实现PAT乙级1029 旧键盘（举一反三+思想解读+逐步优化）五千字好文

一个认为一切根源都是“自己不够强”的INTJ

个人主页：用哲学编程-CSDN博客
专栏：每日一题——举一反三
Python编程学习
Python内置函数

Python-3.12.0文档解读

我的写法

代码评析

时间复杂度

空间复杂度

我要更强

方法一：使用集合来存储不正确的字符

方法二：使用列表来存储错误按键

方法三：使用布尔数组来存储不正确的字符

哲学和编程思想

方法一：使用集合来存储不正确的字符

方法二：使用列表来存储错误按键

方法三：使用布尔数组来存储不正确的字符

总结

举一反三

1. 空间换时间

2. 集合论和数据结构选择

3. 算法复杂度分析

4. 简单性和可读性

5. 测试和调试

6. 学习和实践

题目链接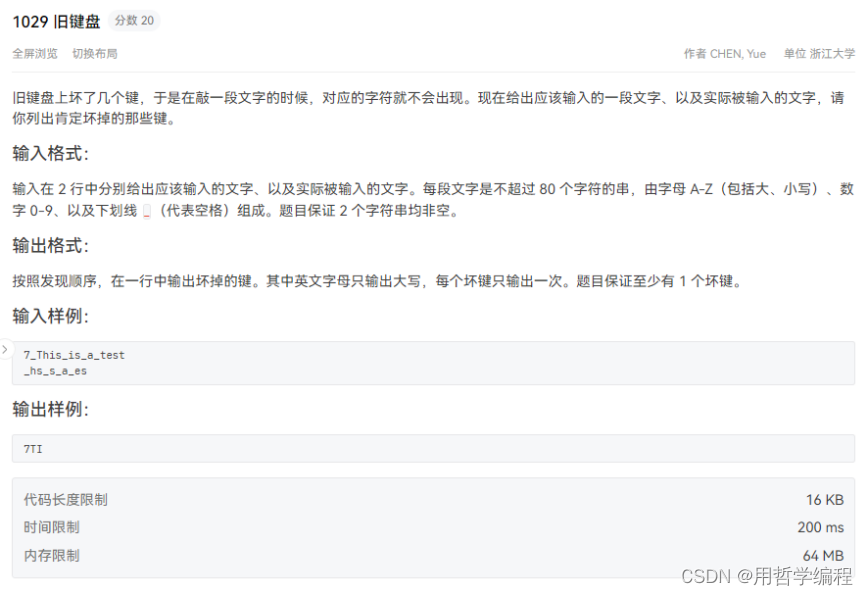

我的写法

# 读取用户输入的字符串，并将其转换为大写
corrects = input().upper()

# 创建一个集合，用于存储错误的按键
bad_keys = set()

# 再次读取用户输入的字符串，并将其转换为大写
incorrects = input().upper()

# 遍历正确字符串的每个字符
for i in range(len(corrects)):
    # 检查当前字符是否存在于不正确的字符串中
    if incorrects.find(corrects[i]) == -1:
        # 如果当前字符不在不正确的字符串中，并且它还没有被添加到错误的按键集合中
        if corrects[i] not in bad_keys:
            # 将该字符添加到错误的按键集合中
            bad_keys.add(corrects[i])
            # 打印出该字符，使用end=''确保字符在同一行输出
            print(corrects[i], end='')

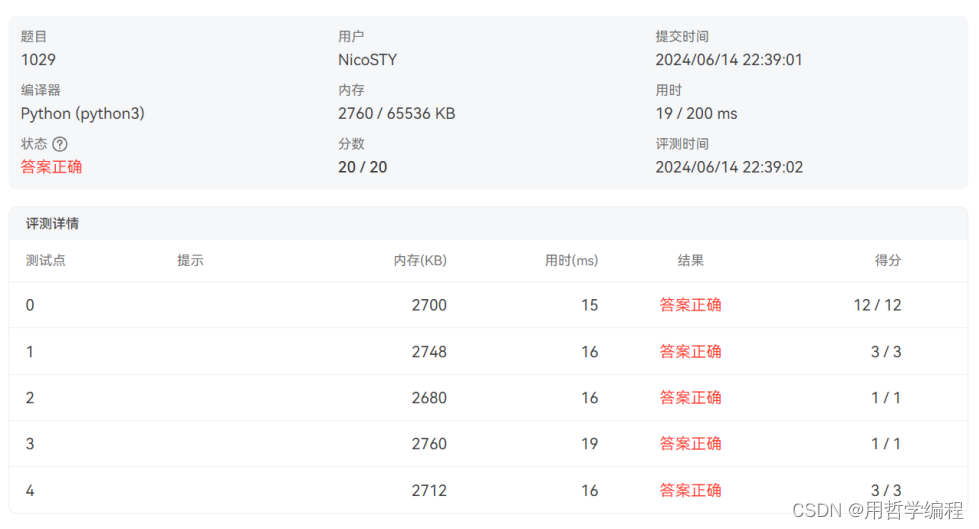
这段代码实现了一个比较简单的功能，即在两个输入字符串中找出那些在第一个字符串中出现但在第二个字符串中没有出现的字符，并且输出这些字符。下面是对这段代码的详细评析，包括时间复杂度和空间复杂度分析。

代码评析

代码逻辑清晰：代码的逻辑比较直接，通过两次读取输入来获取两个字符串，然后依次检查第一个字符串中的每个字符是否存在于第二个字符串中。这种方法直观且容易理解。
使用集合提高查找效率：利用集合 bad_keys 来存储已经发现的并输出过的错误字符。这是一个不错的设计，因为集合具有较高的查找效率（O(1) 平均时间复杂度）。
字符串查找操作：在 incorrects.find(corrects[i]) 中，字符串的 find 方法在最坏情况下的时间复杂度是 O(n)，其中 n 是字符串 incorrects 的长度。由于这是在一个循环内进行的（循环次数为 len(corrects)），因此在最坏情况下，这部分代码的时间复杂度是 O(m * n)，其中 m 是字符串 corrects 的长度，n 是字符串 incorrects 的长度。

时间复杂度

读取输入：这部分时间复杂度可以忽略不计，因为它依赖于用户输入的速度。
遍历 corrects 字符串：这个循环的时间复杂度是 O(m)，其中 m 是 corrects 字符串的长度。
查找字符是否存在于 incorrects 中：使用 find 方法，最坏情况下时间复杂度是 O(n)，其中 n 是 incorrects 字符串的长度。这一步在循环内执行，因此总的时间复杂度是 O(m * n)。
集合操作：在最坏情况下，集合的添加和查找操作的时间复杂度是 O(1)。

总结起来，这段代码的整体时间复杂度是 O(m * n)，其中 m 是 corrects 字符串的长度，n 是 incorrects 字符串的长度。

空间复杂度

字符串存储：两个输入字符串 corrects 和 incorrects 占用的空间是 O(m + n)。
集合 bad_keys：最坏情况下，集合 bad_keys 中可能包含所有正确字符串中的字符，因此占用的空间是 O(m)。

总结起来，这段代码的空间复杂度是 O(m + n)，其中 m 是 corrects 字符串的长度，n 是 incorrects 字符串的长度。

我要更强

当然，有几种优化代码的方式可以同时提高时间复杂度和空间复杂度。我会提供几个方案，并给出完整的代码和注释。

方法一：使用集合来存储不正确的字符

优化思路：通过将 incorrects 转换为集合，可以利用集合的查找效率（O(1)），从而优化时间复杂度。

代码：

# 读取用户输入的字符串，并将其转换为大写
corrects = input().upper()

# 创建一个集合，用于存储不正确的字符
incorrects = set(input().upper())

# 创建一个集合，用于存储已经检测到的错误按键
bad_keys = set()

# 遍历正确字符串的每个字符
for char in corrects:
    # 检查当前字符是否存在于不正确的字符集合中
    if char not in incorrects:
        # 如果当前字符不在不正确的字符集合中，并且它还没有被添加到错误按键集合中
        if char not in bad_keys:
            # 将该字符添加到错误按键集合中
            bad_keys.add(char)
            # 打印出该字符，使用end=''确保字符在同一行输出
            print(char, end='')

时间复杂度：O(m)

遍历 corrects 字符串的时间复杂度是 O(m)。
在 incorrects 集合中查找字符的时间复杂度是 O(1)。

空间复杂度：O(m + n)

存储 corrects 和 incorrects 共占用 O(m + n) 的空间。
存储 bad_keys 的空间是 O(k)，其中 k 是错误按键的数量，最坏情况下 k = m。

方法二：使用列表来存储错误按键

优化思路：列表的空间效率高于集合，如果错误按键数量较少，这种方法可以节省一些空间。

代码：

# 读取用户输入的字符串，并将其转换为大写
corrects = input().upper()

# 创建一个集合，用于存储不正确的字符
incorrects = set(input().upper())

# 创建一个列表，用于存储已经检测到的错误按键
bad_keys = []

# 遍历正确字符串的每个字符
for char in corrects:
    # 检查当前字符是否存在于不正确的字符集合中
    if char not in incorrects:
        # 如果当前字符不在不正确的字符集合中，并且它还没有被添加到错误按键列表中
        if char not in bad_keys:
            # 将该字符添加到错误按键列表中
            bad_keys.append(char)
            # 打印出该字符，使用end=''确保字符在同一行输出
            print(char, end='')

时间复杂度：O(m)

遍历 corrects 字符串的时间复杂度是 O(m)。
在 incorrects 集合中查找字符的时间复杂度是 O(1)。
在列表 bad_keys 中查找字符的时间复杂度是 O(k)，最坏情况下 k = m。

空间复杂度：O(m + n)

存储 corrects 和 incorrects 共占用 O(m + n) 的空间。
存储 bad_keys 的空间是 O(k)，其中 k 是错误按键的数量。

方法三：使用布尔数组来存储不正确的字符

优化思路：如果字符集的范围有限（如仅字母A-Z），可以使用固定大小的布尔数组替代集合，这样可以进一步优化空间和查找效率。

代码：

# 读取用户输入的字符串，并将其转换为大写
corrects = input().upper()

# 创建一个布尔数组，用于标记不正确的字符
incorrects = [False] * 26

# 填充不正确的字符布尔数组
for char in input().upper():
    incorrects[ord(char) - ord('A')] = True

# 创建一个集合，用于存储已经检测到的错误按键
bad_keys = set()

# 遍历正确字符串的每个字符
for char in corrects:
    # 检查当前字符是否存在于不正确的字符布尔数组中
    if not incorrects[ord(char) - ord('A')]:
        # 如果当前字符不在不正确的字符布尔数组中，并且它还没有被添加到错误按键集合中
        if char not in bad_keys:
            # 将该字符添加到错误按键集合中
            bad_keys.add(char)
            # 打印出该字符，使用end=''确保字符在同一行输出
            print(char, end='')

时间复杂度：O(m)

遍历 corrects 字符串的时间复杂度是 O(m)。
在布尔数组中查找字符的时间复杂度是 O(1)。

空间复杂度：O(m + 26)

存储 corrects 需要 O(m) 的空间，布尔数组固定为 26 个元素。
存储 bad_keys 的空间是 O(k)，其中 k 是错误按键的数量，最坏情况下 k = m。

通过这几种方法，可以有效地优化代码的时间复杂度和空间复杂度，具体选择哪种方法可以根据问题的具体场景和输入数据的特点来决定。

哲学和编程思想

这些方法背后应用了一些重要的编程哲学和思想，如空间换时间、集合论、算法复杂度分析和数据结构选择。下面具体说明这些方法中使用的编程哲学和思想：

方法一：使用集合来存储不正确的字符

编程思想：

空间换时间：
- 通过使用集合来存储不正确的字符，牺牲了一部分空间来换取查找操作的高效性（O(1)）。这是一个典型的“空间换时间”的策略，用更多的存储空间来减少时间复杂度。
集合论：
- 集合的数据结构利用哈希表实现了元素的快速查找、添加和删除操作。这种高效的集合操作源于集合论中的基本概念。
数据结构选择：

针对查找频繁且不需要保持顺序的情况，选择集合这种数据结构是非常合适的。集合能快速判断某个元素是否存在，非常适用于这类问题。

方法二：使用列表来存储错误按键

编程思想：

简单性和可读性：
- 使用列表来存储已经检测到的错误按键，这种方法更简单和直观。但在最坏情况下会影响性能（在列表中的查找操作是O(k)）。
时间复杂度分析：

充分理解算法的时间复杂度，通过对算法的时间复杂度进行分析，决定使用合适的数据结构。例如，在这里为了简化代码，选择列表，但要注意最坏情况下的性能影响。

方法三：使用布尔数组来存储不正确的字符

编程思想：

空间换时间：
- 这一方法再一次利用了“空间换时间”的哲学，通过一个固定大小的布尔数组，用更大的空间来换取查找操作的高效性（O(1)）。
数组的使用：
- 在字符集范围有限的情况下，使用数组（布尔数组）来优化性能。这是通过对问题的特性进行分析后做出的数据结构选择。
算法复杂度分析：

充分理解和分析算法的时间和空间复杂度，针对问题的特点选择最优的数据结构和算法。布尔数组在字符集范围有限的情况下，可以极大地提高查找操作的效率。

总结

这些方法背后都体现了一些关键的编程哲学和思想：

空间换时间：
- 通过增加空间使用来换取更快的时间效率，这是高效算法设计中的常见策略。
集合论和数据结构选择：
- 根据具体需求选择合适的数据结构（如集合、列表、数组等），利用其特性来优化算法。集合适合频繁查找操作，数组适合空间固定且范围有限的情况。
算法复杂度分析：
- 对时间复杂度和空间复杂度进行分析，选择最优的算法和数据结构。在设计和优化算法时，这种分析是至关重要的。
简单性和可读性：