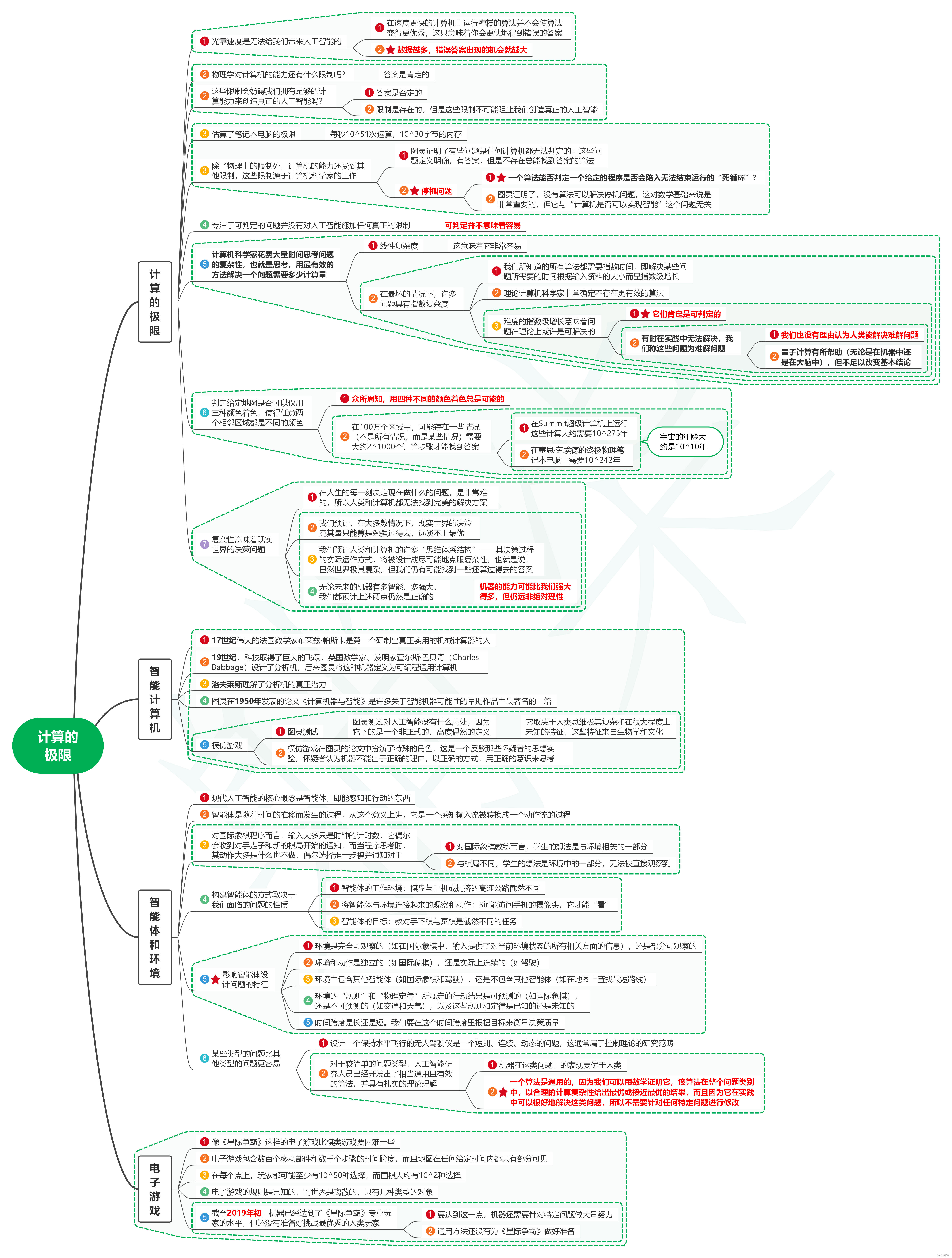
1.       计算的极限

1.1.         光靠速度是无法给我们带来人工智能的

1.1.1.           在速度更快的计算机上运行糟糕的算法并不会使算法变得更优秀，这只意味着你会更快地得到错误的答案

1.1.2.           数据越多，错误答案出现的机会就越大

1.2.         物理学对计算机的能力还有什么限制吗？

1.2.1.           答案是肯定的

1.3.         这些限制会妨碍我们拥有足够的计算能力来创造真正的人工智能吗？

1.3.1.           答案是否定的

1.3.2.           限制是存在的，但是这些限制不可能阻止我们创造真正的人工智能

1.4.         估算了笔记本电脑的极限

1.4.1.           每秒10^51次运算，10^30字节的内存

1.5.         除了物理上的限制外，计算机的能力还受到其他限制，这些限制源于计算机科学家的工作

1.5.1.           图灵证明了有些问题是任何计算机都无法判定的：这些问题定义明确，有答案，但是不存在总能找到答案的算法

1.5.2.           停机问题

1.5.2.1.            一个算法能否判定一个给定的程序是否会陷入无法结束运行的“死循环”？

1.5.2.2.            图灵证明了，没有算法可以解决停机问题，这对数学基础来说是非常重要的，但它与“计算机是否可以实现智能”这个问题无关

1.6.         专注于可判定的问题并没有对人工智能施加任何真正的限制

1.6.1.           可判定并不意味着容易

1.7.         计算机科学家花费大量时间思考问题的复杂性，也就是思考，用最有效的方法解决一个问题需要多少计算量

1.7.1.           线性复杂度

1.7.1.1.            这意味着它非常容易

1.7.2.           在最坏的情况下，许多问题具有指数复杂度

1.7.2.1.            我们所知道的所有算法都需要指数时间，即解决某些问题所需要的时间根据输入资料的大小而呈指数级增长

1.7.2.2.            理论计算机科学家非常确定不存在更有效的算法

1.7.2.3.            难度的指数级增长意味着问题在理论上或许是可解决的

1.7.2.3.1.             它们肯定是可判定的

1.7.2.3.2.             有时在实践中无法解决，我们称这些问题为难解问题

1.7.2.3.2.1.              我们也没有理由认为人类能解决难解问题

1.7.2.3.2.2.              量子计算有所帮助（无论是在机器中还是在大脑中），但不足以改变基本结论

1.8.         判定给定地图是否可以仅用三种颜色着色，使得任意两个相邻区域都是不同的颜色

1.8.1.           众所周知，用四种不同的颜色着色总是可能的

1.8.2.           在100万个区域中，可能存在一些情况（不是所有情况，而是某些情况）需要大约2^1000个计算步骤才能找到答案

1.8.2.1.            在Summit超级计算机上运行这些计算大约需要10^275年

1.8.2.2.            在塞思·劳埃德的终极物理笔记本电脑上需要10^242年

1.8.2.3.            宇宙的年龄大约是10^10年

1.9.         复杂性意味着现实世界的决策问题

1.9.1.           在人生的每一刻决定现在做什么的问题，是非常难的，所以人类和计算机都无法找到完美的解决方案

1.9.2.           我们预计，在大多数情况下，现实世界的决策充其量只能算是勉强过得去，远谈不上最优

1.9.3.           我们预计人类和计算机的许多“思维体系结构”——其决策过程的实际运作方式，将被设计成尽可能地克服复杂性，也就是说，虽然世界极其复杂，但我们仍有可能找到一些还算过得去的答案

1.9.4.           无论未来的机器有多智能、多强大，我们都预计上述两点仍然是正确的

1.9.4.1.            机器的能力可能比我们强大得多，但仍远非绝对理性

2.       智能计算机

2.1.         17世纪伟大的法国数学家布莱兹·帕斯卡是第一个研制出真正实用的机械计算器的人

2.2.         19世纪，科技取得了巨大的飞跃，英国数学家、发明家查尔斯·巴贝奇（Charles

Babbage）设计了分析机，后来图灵将这种机器定义为可编程通用计算机

2.3.         洛夫莱斯理解了分析机的真正潜力

2.4.         图灵在1950年发表的论文《计算机器与智能》是许多关于智能机器可能性的早期作品中最著名的一篇

2.5.         模仿游戏

2.5.1.           图灵测试

2.5.1.1.            图灵测试对人工智能没有什么用处，因为它下的是一个非正式的、高度偶然的定义

2.5.1.1.1.             它取决于人类思维极其复杂和在很大程度上未知的特征，这些特征来自生物学和文化

2.5.2.           模仿游戏在图灵的论文中扮演了特殊的角色，这是一个反驳那些怀疑者的思想实验，怀疑者认为机器不能出于正确的理由，以正确的方式，用正确的意识来思考

3.       智能体和环境

3.1.         现代人工智能的核心概念是智能体，即能感知和行动的东西

3.2.         智能体是随着时间的推移而发生的过程，从这个意义上讲，它是一个感知输入流被转换成一个动作流的过程

3.3.         对国际象棋程序而言，输入大多只是时钟的计时数，它偶尔会收到对手走子和新的棋局开始的通知，而当程序思考时，其动作大多是什么也不做，偶尔选择走一步棋并通知对手

3.3.1.           对国际象棋教练而言，学生的想法是与环境相关的一部分

3.3.2.           与棋局不同，学生的想法是环境中的一部分，无法被直接观察到

3.4.         构建智能体的方式取决于我们面临的问题的性质

3.4.1.           智能体的工作环境：棋盘与手机或拥挤的高速公路截然不同

3.4.2.           将智能体与环境连接起来的观察和动作：Siri能访问手机的摄像头，它才能“看”

3.4.3.           智能体的目标：教对手下棋与赢棋是截然不同的任务

3.5.         影响智能体设计问题的特征

3.5.1.           环境是完全可观察的（如在国际象棋中，输入提供了对当前环境状态的所有相关方面的信息），还是部分可观察的

3.5.2.           环境和动作是独立的（如国际象棋），还是实际上连续的（如驾驶）

3.5.3.           环境中包含其他智能体（如国际象棋和驾驶），还是不包含其他智能体（如在地图上查找最短路线）

3.5.4.           环境的“规则”和“物理定律”所规定的行动结果是可预测的（如国际象棋），还是不可预测的（如交通和天气），以及这些规则和定律是已知的还是未知的

3.5.5.           时间跨度是长还是短。我们要在这个时间跨度里根据目标来衡量决策质量

3.6.         某些类型的问题比其他类型的问题更容易

3.6.1.           设计一个保持水平飞行的无人驾驶仪是一个短期、连续、动态的问题，这通常属于控制理论的研究范畴

3.6.2.           对于较简单的问题类型，人工智能研究人员已经开发出了相当通用且有效的算法，并具有扎实的理论理解

3.6.2.1.            机器在这类问题上的表现要优于人类

3.6.2.2.            一个算法是通用的，因为我们可以用数学证明它，该算法在整个问题类别中，以合理的计算复杂性给出最优或接近最优的结果，而且因为它在实践中可以很好地解决这类问题，所以不需要针对任何特定问题进行修改

4.       电子游戏

4.1.         像《星际争霸》这样的电子游戏比棋类游戏要困难一些

4.2.         电子游戏包含数百个移动部件和数千个步骤的时间跨度，而且地图在任何给定时间内都只有部分可见

4.3.         在每个点上，玩家都可能至少有10^50种选择，而围棋大约有10^2种选择

4.4.         电子游戏的规则是已知的，而世界是离散的，只有几种类型的对象

4.5.         截至2019年初，机器已经达到了《星际争霸》专业玩家的水平，但还没有准备好挑战最优秀的人类玩家

4.5.1.           要达到这一点，机器还需要针对特定问题做大量努力

4.5.2.           通用方法还没有为《星际争霸》做好准备