位运算算法：编程世界中的魔法符号

news2024/11/25 9:57:59

✨✨✨学习的道路很枯燥，希望我们能并肩走下来!

文章目录

前言

一. 常见位运算总结

二、常见位运算题目

2.1 位1的个数

2.2 比特数记位（典型dp）

2.3 汉明距离

2.4 只出现一次的数字（1）

2.5 只出现一次的数字（2）

2.6 只出现一次的数字（3）

2.7 判断字符是否为1

2.8 丢失的数字

2.9 两整数之和

2.10 消失的两个数字

总结

前言

本篇详细介绍了位运算算法的使用，让使用者了解位运算，而不是仅仅停留在表面，文章可能出现错误，如有请在评论区指正，让我们一起交流，共同进步！

一. 常见位运算总结

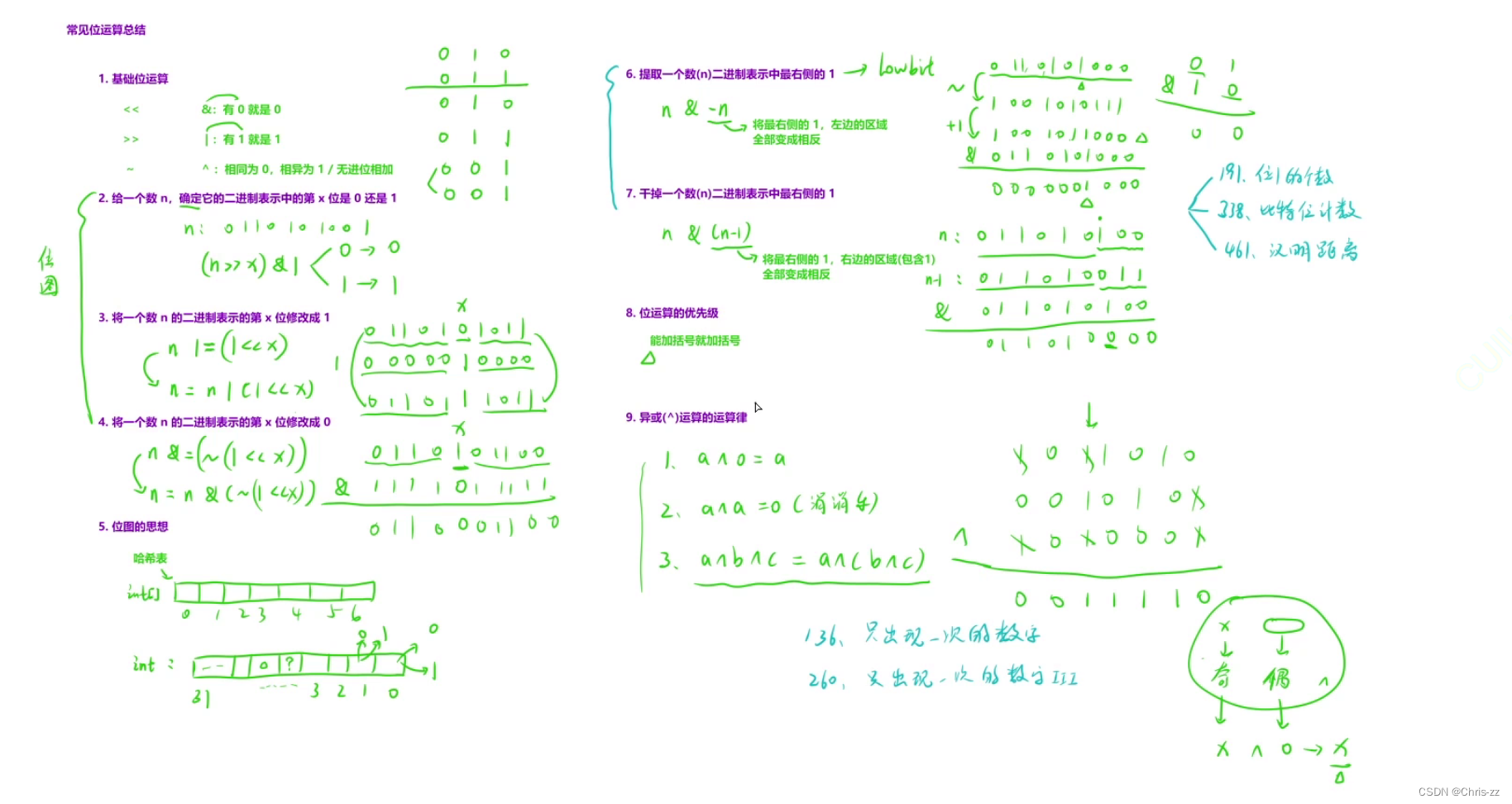
二、常见位运算题目

2.1 位1的个数

191. 位1的个数 - 力扣（LeetCode）

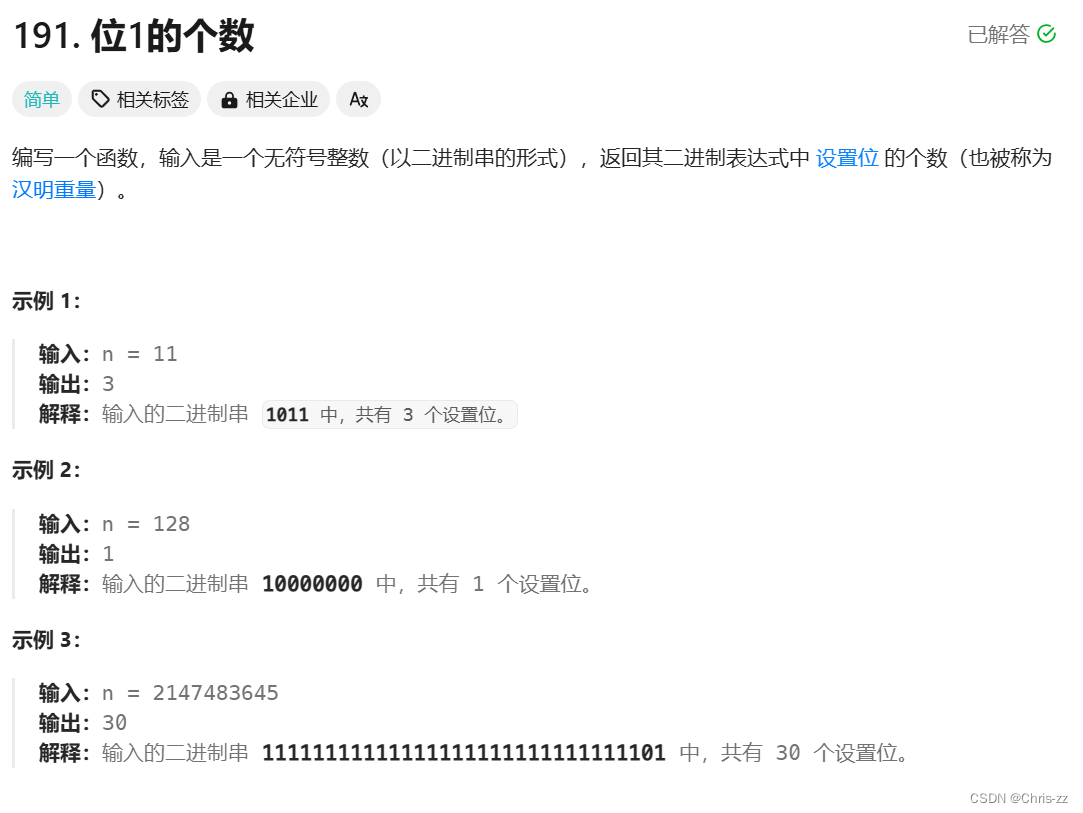利用第七条特性：n&（n-1）干掉最后一个1，然后每次都用count++去统计，直到变成0

class Solution {
public:
    int hammingWeight(int n) {
        int count = 0;
        while(n&(-n))
        {
            n&=(n-1);
            count++;
        }
        return count;
    }
};

2.2 比特数记位（典型dp）

338. 比特位计数 - 力扣（LeetCode）

思路1：每遍历一个数都用n&（n-1）去数他一共有多少个1，然后放ret数组中

class Solution {
public:
    vector<int> countBits(int n) {
        vector<int> ret(n+1);
        for(int i = 0 ;i<=n;i++)
        {
            int m = i;
            int count = 0;
            while(m&(-m))
            {
                m&=(m-1);
                count++;
            }
            ret[i] = count;
        }
        return ret;

    }
};

思路2：简单dp（前缀和 + 位运算

我们发现第i个位置的1的个数等于第i-1位置的1的个数+1

class Solution {
public:
    vector<int> countBits(int n) {
        vector<int> ret(n+1);
        for(int i = 1 ;i<=n;i++)
        {
            ret[i] = ret[i&(i-1)] + 1;
        }
        return ret;

    }
};

2.3 汉明距离

461. 汉明距离 - 力扣（LeetCode）

利用异或相同为0相异为1的特点，x和y异或后不一样的位都会变成1，这个时候再用n&（n-1）去统计1个个数，即为这两个数字的汉明距离

class Solution {
public:
    int hammingDistance(int x, int y) 
    {
      //异或的特点，相同为0，相异为1     然后再利用n&(n-1)统计1的个数
      int n=x^y;
      int count=0;
      while(n)
      {
        n&=(n-1);
        ++count;
      }
      return count;
    }
};

2.4 只出现一次的数字（1）

136. 只出现一次的数字 - 力扣（LeetCode）

思路：利用异或的性质，出现两次的数异或后为0，出现一次的数异或0还是本身

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int value = 0;
        for(auto &e : nums)
        {
            value^=e;
        }
        return value;
    }
};

2.5 只出现一次的数字（2）

137. 只出现一次的数字 II - 力扣（LeetCode）

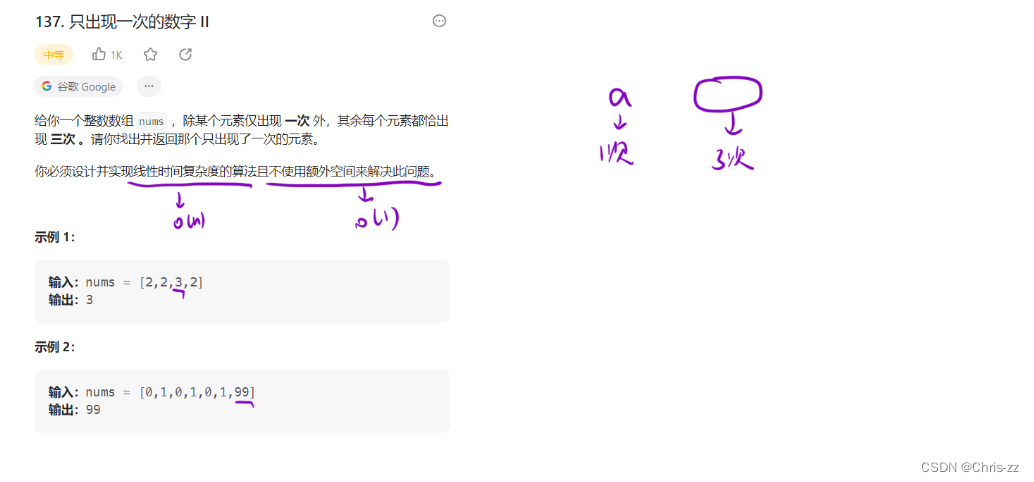
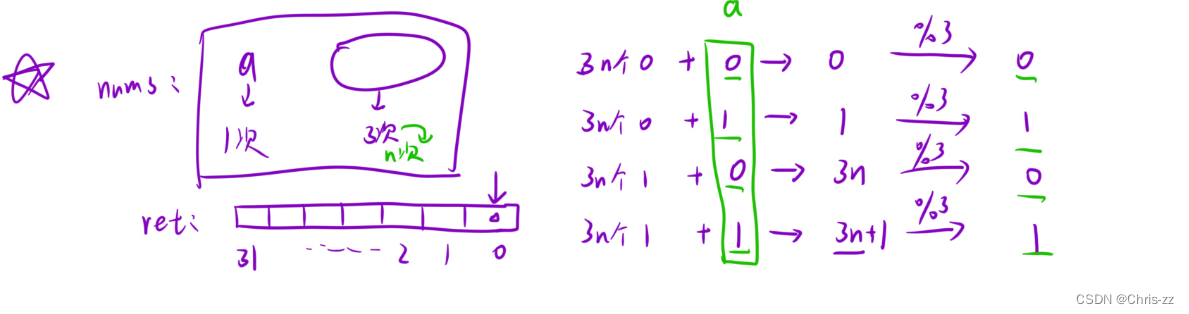
具体地，考虑答案的第 iii 个二进制位（iii 从 000 开始编号），它可能为 000 或 111。对于数组中非答案的元素，每一个元素都出现了 333 次，对应着第 iii 个二进制位的 333 个 000 或 333 个 111，无论是哪一种情况，它们的和都是 333 的倍数（即和为 000 或 333）。因此：

答案的第 iii 个二进制位就是数组中所有元素的第 iii 个二进制位之和除以 333 的余数。

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int ans = 0;
        for (int i = 0; i < 32; ++i) {


            // 统计该每个数字第i个比特位为1的总数
            int total = 0;
            for (int num: nums) {
                total += ((num >> i) & 1);
            }


            // 如果total能够被3整除，说明只出现一次的数字在该位置上一定是0
            // 否则在该位置上一定是1
            if (total % 3) {
                ans |= (1 << i);
            }
        }
        return ans;
    }
};

2.6 只出现一次的数字（3）

260. 只出现一次的数字 III - 力扣（LeetCode）

class Solution {
public:
    vector<int> singleNumber(vector<int>& nums) 
    {
       unsigned int temp=0;//遇到INT_MIN会溢出，10000……00
       for(int num:nums) temp^=num;
       int x=temp&(-temp);//x拿到最后一个1，即两个数不同的地方
       //int x= (temp == temp ? temp : temp & (-temp));
       int type1=0,type2=0;
       for(int num:nums) if(num&x) value1^=num; else value2^=num;
       return {value,value};
    }
};

一般解法：

class Solution {
public:
    vector<int> singleNumber(vector<int>& nums) {
    sort(nums.begin(), nums.end());
    vector<int> res;
    int i = 0;
    for (; i < nums.size() - 1; ) 
    {
      if (nums[i] == nums[i + 1]) 
      {
        i += 2;
      } 
      else 
      {
        res.push_back(nums[i]);
        i += 1;
      }
    }
    if (i < nums.size()) 
    {
      res.push_back(nums[i]);
    }
    return res;     
  }
};

2.7 判断字符是否为1

面试题 01.01. 判定字符是否唯一 - 力扣（LeetCode）

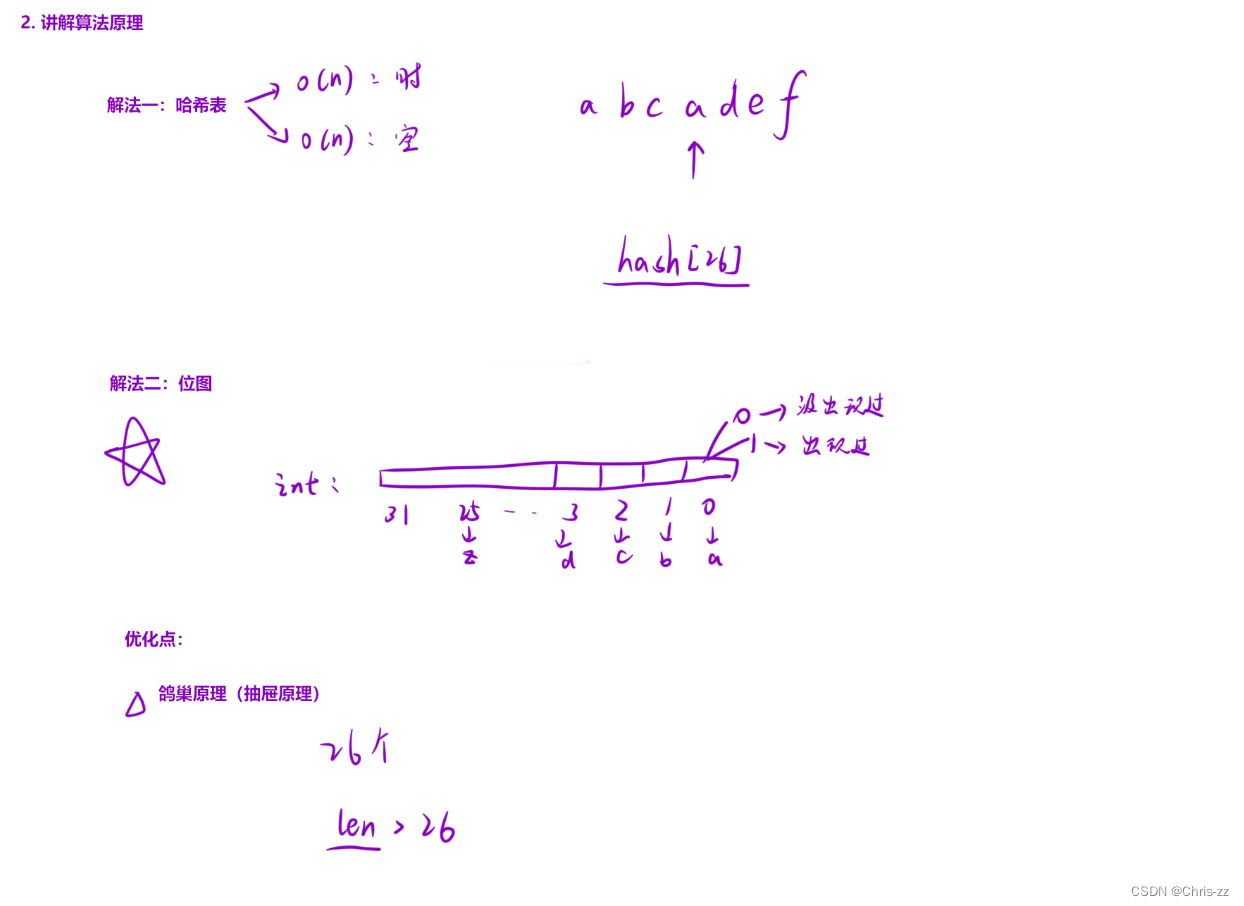
class Solution {
public:
    bool isUnique(string astr) {
        // 利用鸽巢原理做优化
        if(astr.size()>26) return false;

        int bitMap = 0;
        for(auto& ch : astr)
        {
            int i = ch - 'a';
            // 先判断字符是否出现过
            if((bitMap>>i) & 1 == 1) return false;
            // 将当前字符加入到位图中
            bitMap |= (1<<i);
        }
        return true;
    }
};

2.8 丢失的数字

268. 丢失的数字 - 力扣（LeetCode）

思路1：高斯公式

class Solution {
public:
    int missingNumber(vector<int>& nums) {
        int n = nums.size();
        int ret = ((0 + n)*(n+1))/2;
        for(auto& e : nums)
        {
            ret -= e;
        }
        return ret;
    }
};

思路2：异或运算

class Solution {
public:
    int missingNumber(vector<int>& nums) {
        int n = nums.size();
        int ret = 0;
        for(auto& e : nums) ret^=e;
        for(int i = 0;i<=n;i++) ret^=i;
        return ret;
    }
};

2.9 两整数之和

371. 两整数之和 - 力扣（LeetCode）

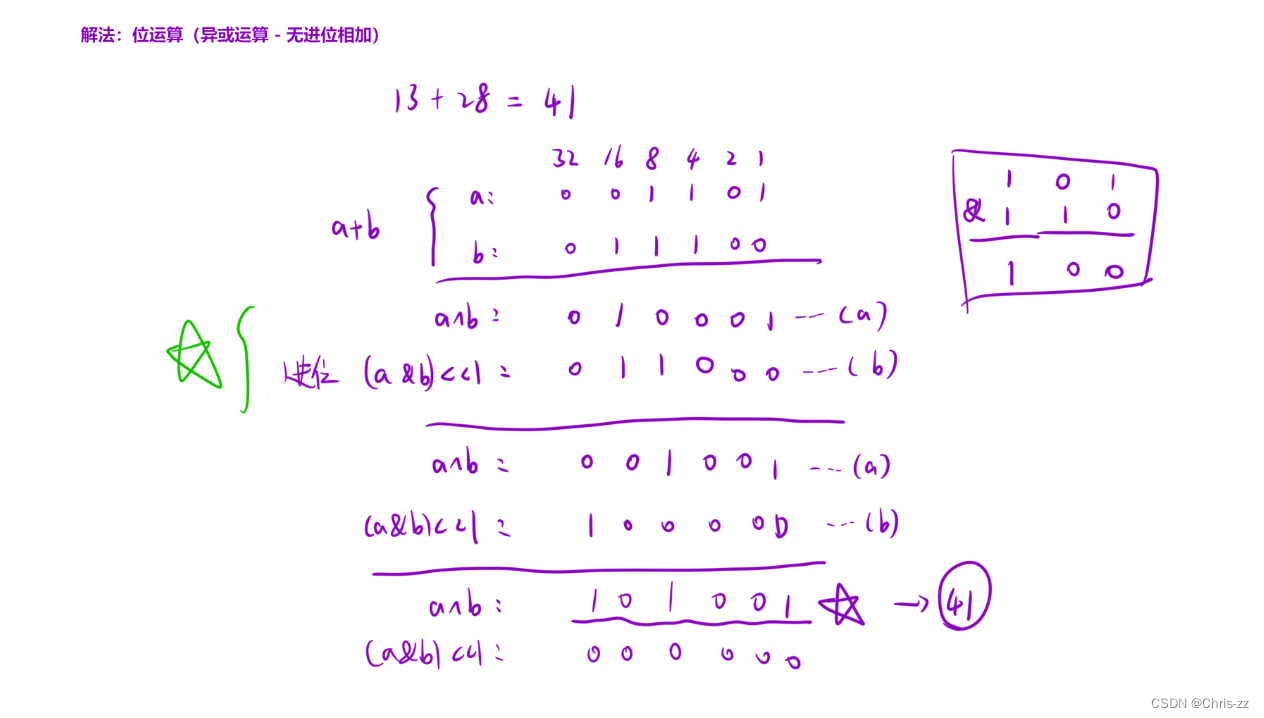
class Solution {
public:
    int getSum(int a, int b) {
        while(b != 0)
        {
            int x = a^b; //先算出无进位相加的结果
            unsigned int carry = (unsigned int)(a&b)<<1; //算出进位，//要考虑-1，因为-1的右移操作是没有定义的
            a = x;
            b = carry;
        }
        return a;
    }
};

2.10 消失的两个数字

面试题 17.19. 消失的两个数字 - 力扣（LeetCode）

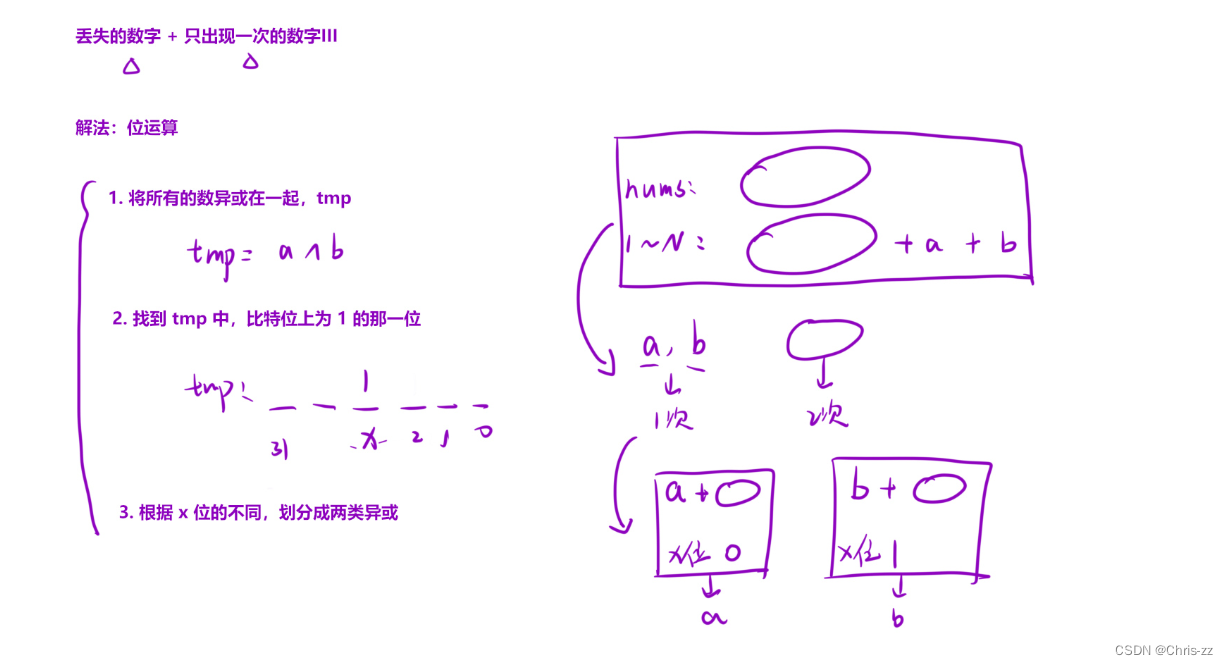
class Solution {
public:
    vector<int> missingTwo(vector<int>& nums) {
        //1.将所有的数异或在一起
        int tmp = 0;
        for(auto& e : nums)
            tmp^=e;
        for(int i = 1;i<=nums.size()+2;i++)
            tmp^=i;
        //2. 找a，b中比特位不同的那一位
        int x = tmp&(-tmp);
        // 3. 根据比特位不同的那一位，划分成两类来异或
        int a = 0, b = 0;
        for(auto& e : nums)
        {
            if(e&x) a^=e;
            else    b^=e;
        }
        for(int i=1;i<=nums.size()+2;++i)
        {
            if(i&x) a^=i;  
            else  b^=i;
        }
        return {a,b};
    }
};