java高级——Arrays工具类
- 前情提要
- 文章介绍
- 提前了解的知识点
- 1 二分查找思想
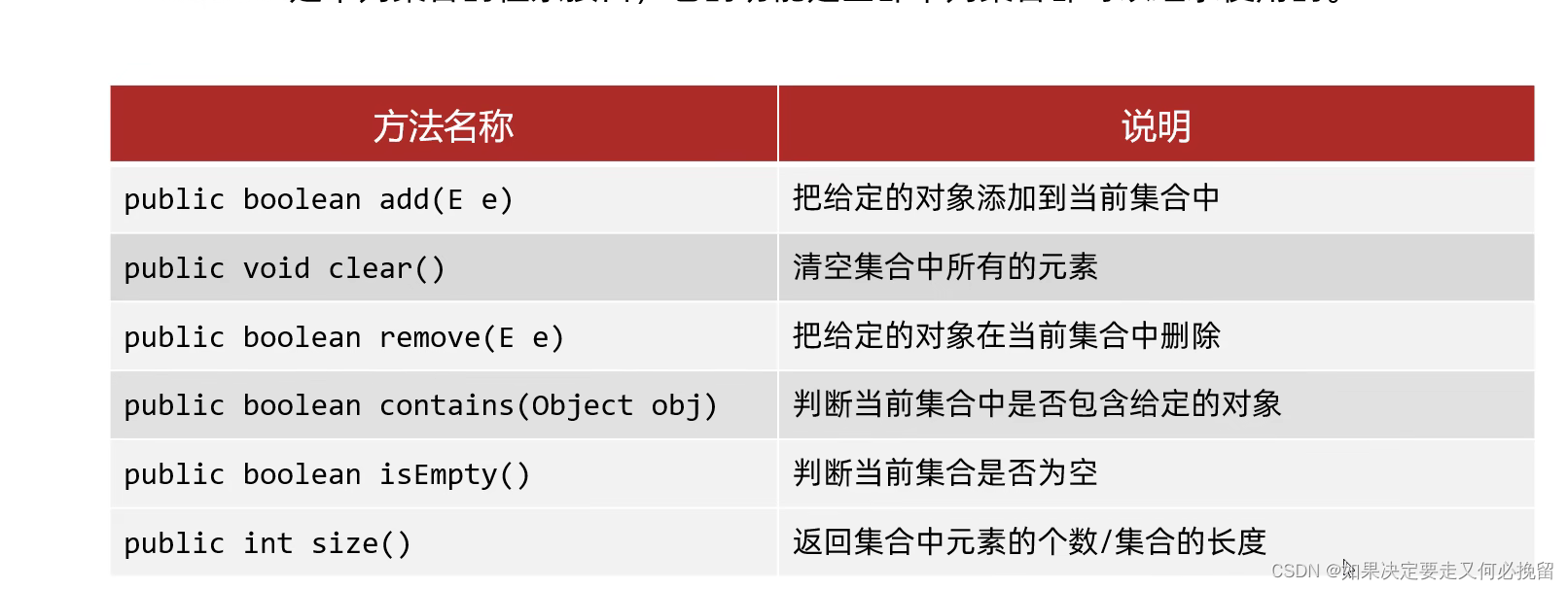
- Arrays常用方法介绍(8大类)
- 1. 创建数组
- 1.1 copyOf()
- 1.2 copyOfRange()
- 1.3 fill()
- 2. 数组转集合:Arrays.asList(常用,也可称为快速初始化集合)
- 3. 数组比较
- 3.1 equals()方法(全部比较以及部分比较)
- 3.2 deepEquals()方法
- 3.3 hashCode()比较
- 4. 数组排序(重点讲解归并排序以及二分排序)
- 4.1 普通sort()排序
- 4.2 增强parallelSort()排序(适用于大数据量)
- 4.3 归并排序(legacyMergeSort)
- 4.5 jdk1.8新排序算法(融合`二分插入排序`binarySort()和`归并排序`mergeSort())
- 5. 数组查询(binarySearch二分查找)
- 6. 数组转Stream流(Arrays.stream)
- 7. 数组打印(Arrays.deepToString)
- 8. 数组填充(setAll和parallelPrefix)
- 总结
- 下期预告
前情提要
上一篇文章我们探索了Collection家族中List集合,包含了ArrayList、LinkedList、Vector等底层实现和区别,这一篇主要围绕Arrays工具类进行探索,对List集合进行扩展。
java高级——Collection集合之List探索
文章介绍
Arrays工具类大多数是对数组进行的简化操作,而ArrayList的底层就是基于数组实现的,具有一定的研究意义,不过经过资料和自证发现其实实际在开发中使用的并不多,因为Stream已经占据了集合操作的大部分,本文将着重介绍常用的操作和思想,有三点:二分查找和快速创建数组以及我们的归并排序和二分排序。
提前了解的知识点
1 二分查找思想
二分查找思想是一个非常重要的思想,大大简化了查询的方式,效率非常高,但势必是有缺陷的,那就是数组必须是有序的,排除这个影响那是非常棒。
简单用文字说明一下什么是二分查询,当一个数组经过排序后,整个数组中的数据就变得非常清晰了,第二个数据一定比第一个大或者小,那么当我们查找指定的数据时,平常的思路都是遍历整个数组进行查询,而二分法则是先寻找中间的数据和查找的数据进行比较,因为有序的前提,瞬间就排除了一半的数据,依此类推,相当于寻址的次数就少了很多,如果有8条数据,寻找最后一条,普通的查询需要寻址8次,而二分法只需要3次,相当于指数倍缩减寻址次数。有兴趣的伙伴瞅一下下面这篇博客,讲得很详细。
什么是二分查找
Arrays常用方法介绍(8大类)
1. 创建数组
1.1 copyOf()
见名知意,这是一个复制的方法,作用就是复制一个新的数组,可指定长度(可以复制从头开始的一部分)。
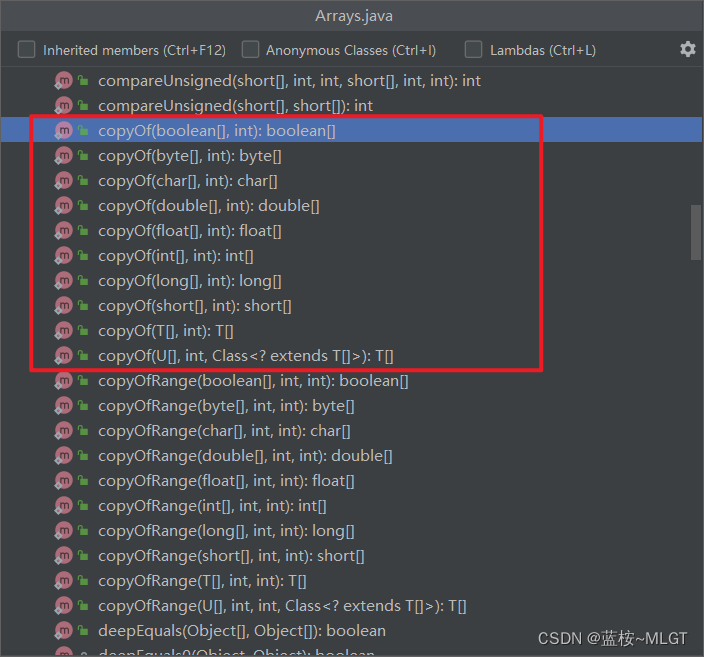
上图看copyOf一共有10中重载方法,每一种所对应的参数不同,包含了基本类型和任意的未知类型(很优美,不愧是源码),其实最终的实现都是一个核心的方法System.arraycopy,这是一个native方法,不需要深究哈,我们在ArrayList的copy方法中也讲到过。
// 默认两个起始位置都是0,目标数组是new的,复制的长度是用户自定义的
System.arraycopy(original, 0, copy, 0, Math.min(original.length, newLength));
// src:原数组
// srcPos: 原数组的起始位置
// dest:目标数组
// destPos: 目标数组的起始位置
// length: 要复制的长度
public static native void arraycopy(Object src, int srcPos,
Object dest, int destPos,
int length);
接下来看一个例子就更清晰了。
public static void main(String[] args) {
String[] test = {"1", "2", "3"};
// 复制了一个长度为2的数组,数据为原数组最开始的两个元素
String[] strings = Arrays.copyOf(test, 2);
// strings = [1, 2]
System.out.println("strings = " + Arrays.toString(strings));
// test = [1, 2, 3]
System.out.println("test = " + Arrays.toString(test));
}
1.2 copyOfRange()
见名知意,这是copyOf的升级版,是带范围的复制数组,相对与copyOf多了一个参数,简单分析一下。
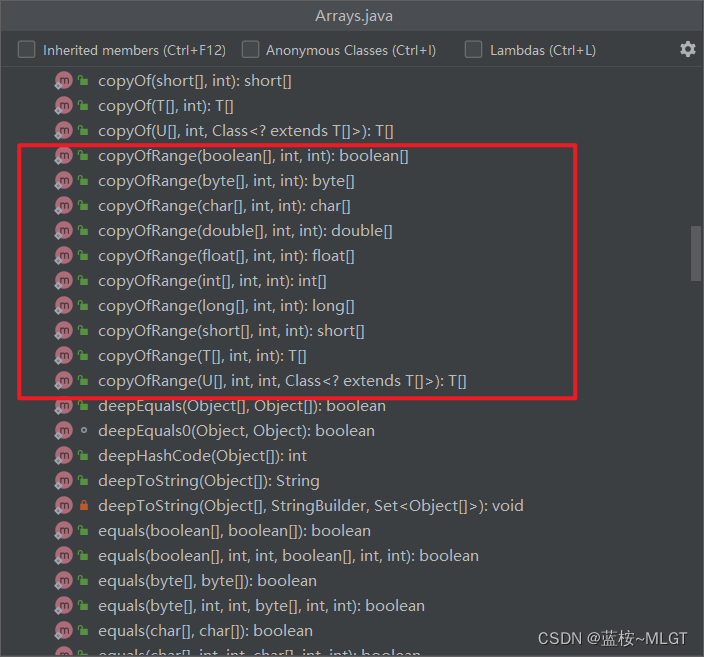
// from:起始下标,to:结束下标
public static byte[] copyOfRange(byte[] original, int from, int to) {
// 复制的数组长度
int newLength = to - from;
if (newLength < 0)
throw new IllegalArgumentException(from + " > " + to);
byte[] copy = new byte[newLength];
// 这里的主要区别是取了一个最小值
System.arraycopy(original, from, copy, 0,
Math.min(original.length - from, newLength));
return copy;
}
public static void main(String[] args) {
String[] test = {"1", "2", "3"};
// 复制了一个长度为2的数组,数据为原数组最开始的两个元素
String[] strings = Arrays.copyOf(test, 2);
// strings = [1, 2]
System.out.println("strings = " + Arrays.toString(strings));
// test = [1, 2, 3]
System.out.println("test = " + Arrays.toString(test));
String[] strings1 = Arrays.copyOfRange(test, 1, 2);
// strings1 = [2]
System.out.println("strings1 = " + Arrays.toString(strings1));
}
简单唠唠这个方法,说是复制数组,其实就是变相的截取数组,因为数组在创建之初是确定好长度的,无法截取,只能通过复制操作达到截取的目的,而通过源码可以看到实现方式,稍有区别,不过这个方法虽然更加灵活,但需要注意的也不少,源码中只是判断了from不能大于to,但是没说下标不能为负数,如果你给负数肯定是报错,不过非常不建议,这种错误是native代码中报的,不好捕捉,尽量在执行前进行参数的校验。
1.3 fill()
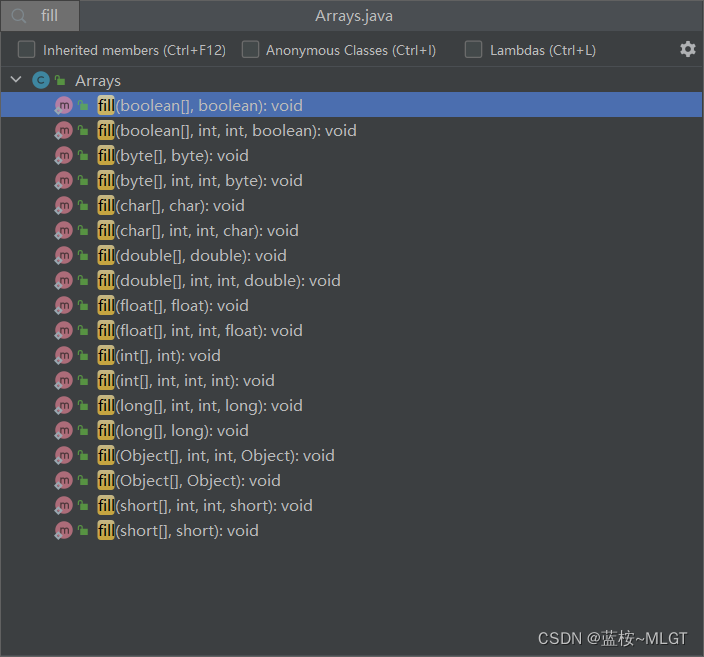
这是一个初始化数组元素为指定值的方法,就是整个数组将会是同一个元素,不太常见,上面介绍的17种重载实现的效果差不多,除了参数类型不同外,还有一个区别就是可以指定区间进行填充,有fromIndex和endIndex参数。
public static void main(String[] args) {
String[] test = new String[3];
Arrays.fill(test, "test");
// test = [test, test, test]
System.out.println("test = " + Arrays.toString(test));
String[] test1 = new String[3];
Arrays.fill(test1, 0, 1, "test");
// test1 = [test, null, null]
System.out.println("test1 = " + Arrays.toString(test1));
}
2. 数组转集合:Arrays.asList(常用,也可称为快速初始化集合)
这是开发中常用的初始化数组手段,相比于普通的给List中一个一个add元素很快捷,不过要注意的是,此时返回的List是java.util.Arrays.ArrayList类型,不支持动态增删,但是可以修改和查看,一般我们是用于初始化一个静态集合,只是用于读取和查看,相当于常量。
List<String> list = Arrays.asList("hello", "world");
// list = [hello, world]
System.out.println("list = " + list);
List<User> users = Arrays.asList(new User("张三", "1"), new User("李四", "2"));
// users = [User{name='张三', sex='1'}, User{name='李四', sex='2'}]
System.out.println("users = " + users.toString());
上面一般是将数组转为集合的方法,有一定缺陷,而下面也是开发中常见的一种快速初始化数组,同样适用于map,而且数组也可以动态的增删。
List<User> userList = new ArrayList<User>(){{
add(new User("王五", "3"));
}};
userList.add(new User("1", "2"));
System.out.println("userList = " + userList);
3. 数组比较
数组也是使用频率较高的一个方法,在ArrayList中我们曾说过其中的equals方法,大概就是说先对两个集合的内存地址比较,之后是长度和修改次数,最后则是每个元素的equals方法,而Arrays中的数组比较类似,一共有3个方法可以使用。
3.1 equals()方法(全部比较以及部分比较)
最常用的比较方法(全部比较)。
public static boolean equals(Object[] a, Object[] a2) {
// 内存地址比较
if (a==a2)
return true;
if (a==null || a2==null)
return false;
int length = a.length;
// 长度比较
if (a2.length != length)
return false;
// 如果长度相等,则比较对应位置的元素是否全部相等
for (int i=0; i<length; i++) {
if (!Objects.equals(a[i], a2[i]))
return false;
}
return true;
}
指定范围进行比较,这种情况适用于不用复制数组来判断两个数组的某一段数据是否相等,同时也有一个重载方法,最后一个参数是Comparator<? super T> cmp,更加灵活的定制比较器。
// a和b分别为两个比较的数组,跟着的就是需要比较的范围
public static boolean equals(Object[] a, int aFromIndex, int aToIndex,
Object[] b, int bFromIndex, int bToIndex) {
// 检查范围是否越界
rangeCheck(a.length, aFromIndex, aToIndex);
rangeCheck(b.length, bFromIndex, bToIndex);
// 检查是否是同一个范围,如果不是则直接返回false
int aLength = aToIndex - aFromIndex;
int bLength = bToIndex - bFromIndex;
if (aLength != bLength)
return false;
// 检查指定范围内所有的对象是否相同
for (int i = 0; i < aLength; i++) {
if (!Objects.equals(a[aFromIndex++], b[bFromIndex++]))
return false;
}
return true;
}
String[] a1 = {"1", "2", "5"};
String[] a2 = {"1", "2", "6"};
boolean equals = Arrays.equals(a1, 0, 2, a2, 0, 2);
// 输出:true
System.out.println("equals = " + equals);
剩余的方法都是其他数据类型的重载方法,目前看就这两种是值得研究的比较方法。
3.2 deepEquals()方法
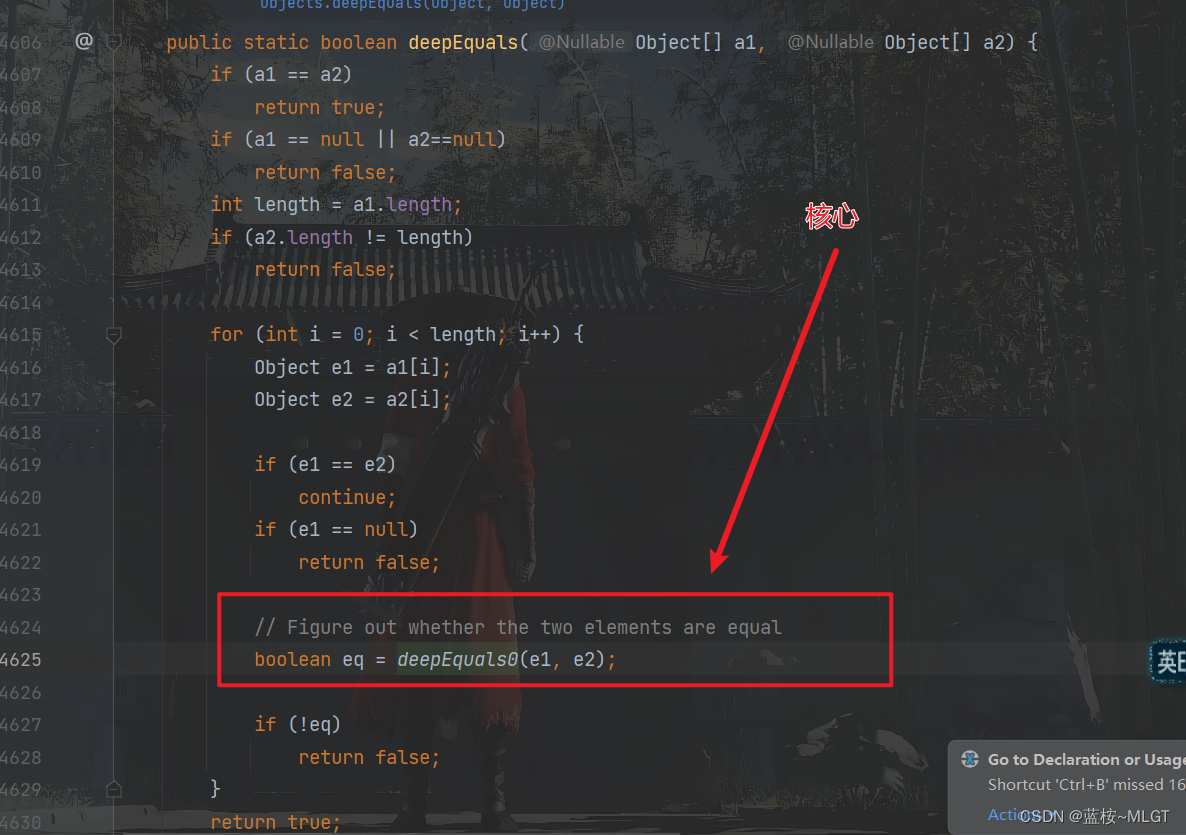
深度比较方法,上面这个图展现了这个方法最核心的是deepEquals0这个方法,其余大差不差。这个方法存在的意义是当我们的数组中元素不只是简单数据类型时也可以完美比较出是否一致,比如说数组中存在另一个数组的情况。
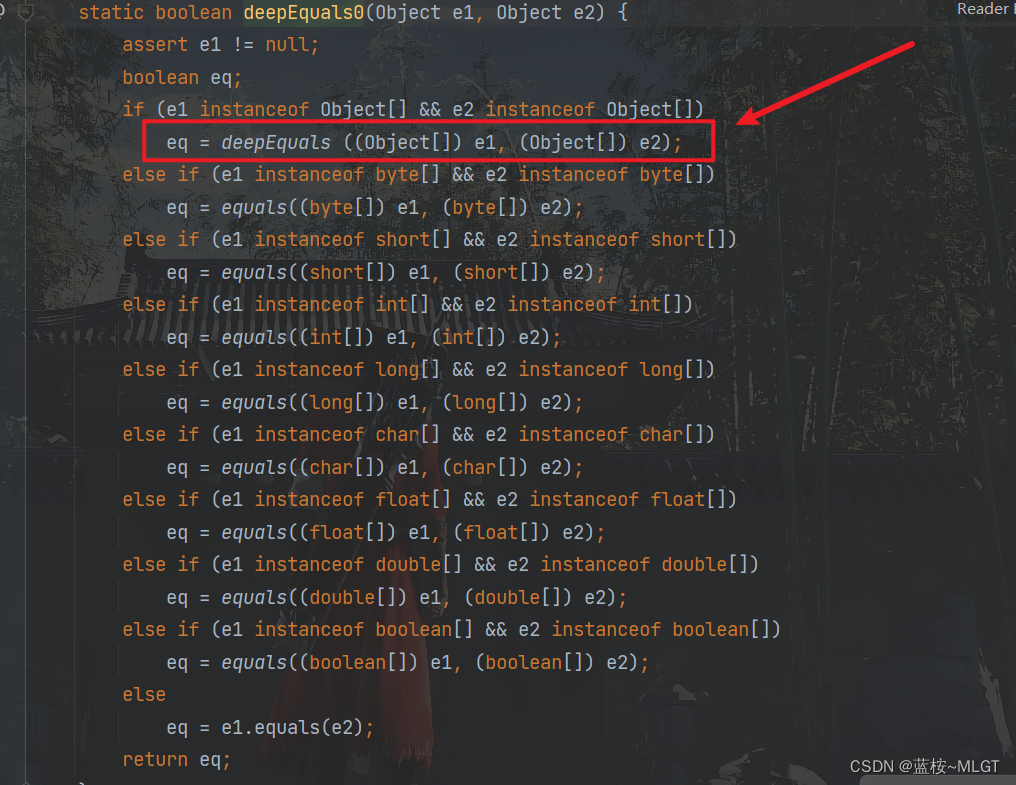
如果说数组中存在的元素是另外一个数组,那就会通过上面这个方法进行递归调用(有点递归的意思),这样就可以做到深度比较。
3.3 hashCode()比较
public static int hashCode(Object a[]) {
if (a == null)
return 0;
int result = 1;
// 可能会存在元素为空,计算出来的hashcode相等的情况
for (Object element : a)
result = 31 * result + (element == null ? 0 : element.hashCode());
return result;
}
通过比较两个数组的hashCode也可以比较是否相等,按照正常情况来说,两个对象的hashCode相等,则这两个对象一定是相等的,但放在数组中可能会存在个例,因为最终返回的是一个不断叠加的hashCode值,如果存在元素为null的情况,hashCode值就是0了,所以说这个方法还是不建议使用。
4. 数组排序(重点讲解归并排序以及二分排序)
数组中我们大多数使用的排序都是简单的数字排序或者字母排序,如果是对象数组则多半会选择集合的stream流+Comparable比较,因为对象集合排序都是基于对象某个属性或者多个属性进行排序,使用数组倒是不太好,这里重点介绍一种归并排序的思路,其中很多排序都用这个思路进行实现。
4.1 普通sort()排序
上面的这么多方法大致分为三种,一种是简单类型的排序,一种是简单类型的范围排序,一种则是对象的排序(不介绍,用stream实现更好),这里说一下前面两种。
- 普通排序(默认升序)
String[] a3 = {"1", "3", "2"};
String[] a5 = {"abe", "abc", "ba"};
Arrays.sort(a3);
Arrays.sort(a5);
// a3 = [1, 2, 3]
System.out.println("a3 = " + Arrays.deepToString(a3));
// a5 = [abc, abe, ba]
System.out.println("a5 = " + Arrays.deepToString(a5));
- 指定范围排序
String[] a6 = {"abe", "ba", "as"};
Arrays.sort(a6, 1, 3);
// a3 = [abe, as, ba]
System.out.println("a3 = " + Arrays.deepToString(a6));
4.2 增强parallelSort()排序(适用于大数据量)
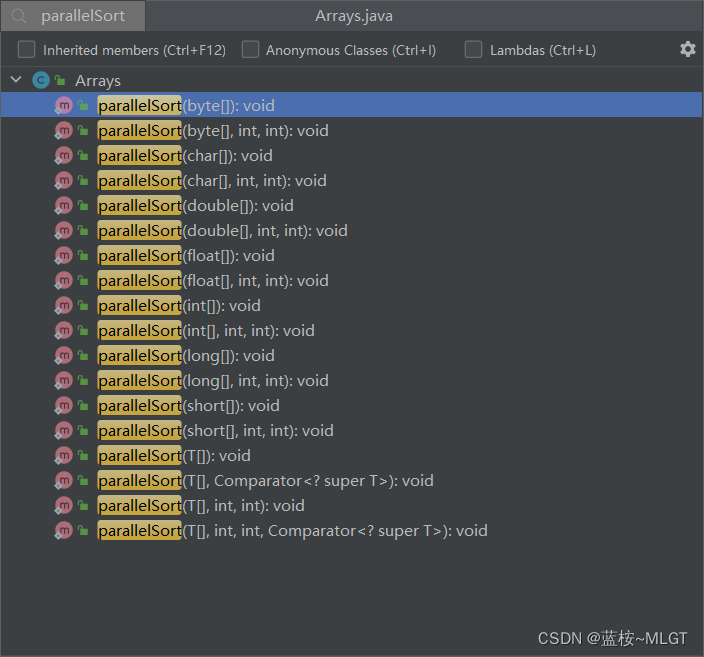
这个方法在使用上和sort相同,都有整体排序和部分排序的功能,不过区别就在于这个方法适用于大数据量的排序,底层使用了并行排序-合并排序算法,就是将数组拆分为多个小的数组并行排序,之后进行合并,大大提高了效率。
4.3 归并排序(legacyMergeSort)
到底什么是归并排序,为什么要使用归并排序呢?
从定义上来讲,归并排序的核心是两个,一个是“分”,一个是“治”,简单来讲就是将一个大数组不断进行均分,直到剩余一个元素,之后各个最小单位进行排序,最后进行合并,能大大节省时间,是不是有点像接力传西瓜一样。
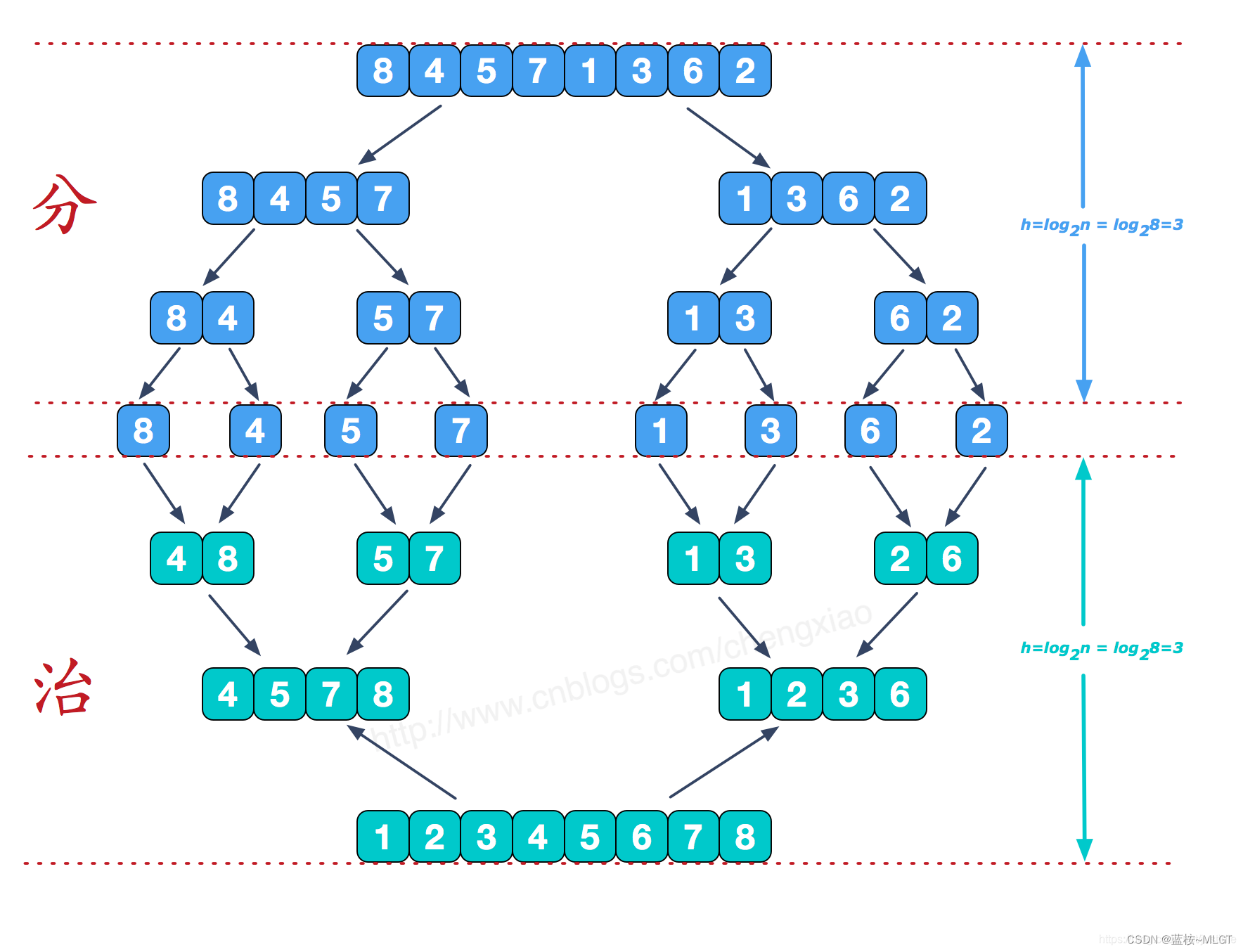
详细请了解这篇博客,非常推荐:归并排序
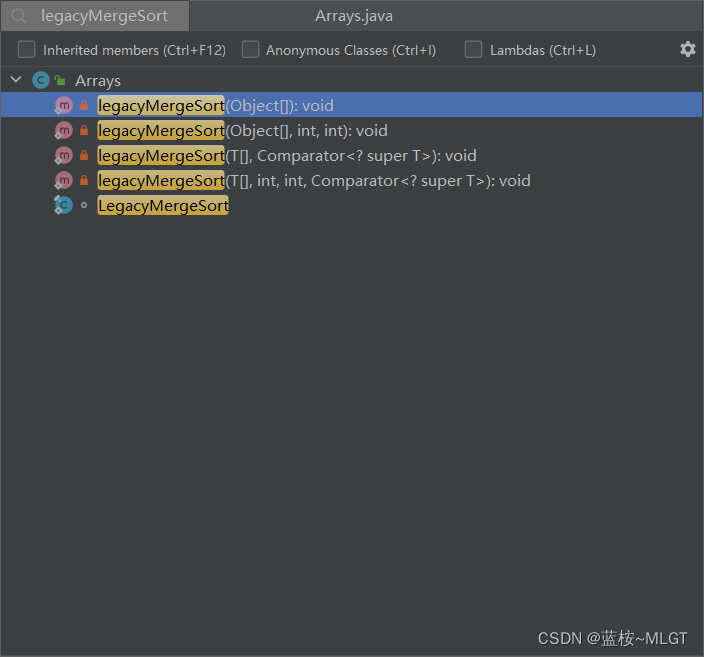
在Arrays工具类中主要实现归并排序的第一是上面这种方法,当然这是jdk1.8之前的实现方式,这里简单分析一下怎么实现的,重点是理解归并排序的思路,我们直接将源码提出来模拟为一个方法进行分析。
public static void main(String[] args) {
Integer[] array = {2, 1, 8, 4, 9, 3, 6, 7, 10, 30, 21, 32, 18, 29, 39, 100, 30};
Integer[] descArray = Arrays.copyOf(array, array.length);
mergeSort(array, descArray, 0, array.length, 0);
// Arrays.deepToString(array) = [1, 2, 3, 4, 6, 7, 8, 9, 10, 18, 21, 29, 30, 30, 32, 39, 100]
System.out.println("Arrays.deepToString(array) = " + Arrays.deepToString(array));
}
/**
*
* @param src 需要排序的数组
* @param dest 一般是复制要排序的数组
* @param low 一般为0
* @param high 一般为数组长度
* @param off 一般为0
*/
public static void mergeSort(Object[] src,
Object[] dest,
int low,
int high,
int off) {
int length = high - low;
// 7 = INSERTIONSORT_THRESHOLD
// jdk1.8前如果分割后的数组长度小于7,采用插入排序,循环套循环比较后切换位置
if (length < 7) {
for (int i=low; i<high; i++)
for (int j=i; j>low &&
((Comparable) dest[j-1]).compareTo(dest[j])>0; j--)
// 交换位置的方法
swap(dest, j, j-1);
return;
}
int destLow = low;
int destHigh = high;
low += off;
high += off;
// 移位运算,左移一位相当于对半砍
int mid = (low + high) >>> 1;
// 递归调用,每次切割后将切割的两个数组分别再次调用此函数,最终执行上面的插入排序
// 注意了:这里交换了desc和src的顺序,其实后面排序的就是src
mergeSort(dest, src, low, mid, -off);
mergeSort(dest, src, mid, high, -off);
// 这里有个优化,如果左边最大的元素小于右边最小的,表示数组已经排序完毕
// 这里已经代表两个分割后的数组完成了排序,所以这个判断成立
// 这里的返回一定是最后执行的
if (((Comparable)src[mid-1]).compareTo(src[mid]) <= 0) {
System.arraycopy(src, low, dest, destLow, length);
return;
}
// 这里进行归并排序,通过代码可以看到这里实际是归并排序的第二核心:治
// 这里分割后的两个数组排好序了,仔细看下,比较首先是左边排好序的最小值和右边排好序的最小值比较
// 依次类推,不用嵌套循环,只执行两个数组合并长度的循环
// 这里可能有人疑惑,为啥排序的是desc,因为上面交换了位置
for(int i = destLow, p = low, q = mid; i < destHigh; i++) {
if (q >= high || p < mid && ((Comparable)src[p]).compareTo(src[q])<=0)
dest[i] = src[p++];
else
dest[i] = src[q++];
}
}
private static void swap(Object[] x, int a, int b) {
Object t = x[a];
x[a] = x[b];
x[b] = t;
}
4.5 jdk1.8新排序算法(融合二分插入排序binarySort()和归并排序mergeSort())
这一小节应该是本篇文章最核心的知识点了,经过大量资料查询和融合,最终整理出来了java中最新的排序算法,据说是最快的排序,话不多说直接来。
参考这篇博客,这里面最香的还是讲解了两种排序的实现思路,用流程图的形式,非常清晰明了,我将在此基础上掺杂更详细的代码分析,建议还是先看一下这篇博客。
世界上最快的排序算法-Timsort
public static void sort(Object[] a) {
if (LegacyMergeSort.userRequested)
legacyMergeSort(a);
else
ComparableTimSort.sort(a, 0, a.length, null, 0, 0);
}
上面是Arrays中常用的排序算法,上面4.3说了legacyMergeSort是为了兼容之前的版本做的归并排序,现在使用的都是ComparableTimSort.sort这个方法,这个方法有两种实现方式。先来说第一种
二分插入排序:
// 先不用纠结这么多参数是干什么的,只需要知道a是排序的数组,lo是0也就是数组起始下标
// hi是数组长度,默认全部排序,其余暂时用不到,都是null和0
static void sort(Object[] a, int lo, int hi, Object[] work, int workBase, int workLen) {
assert a != null && lo >= 0 && lo <= hi && hi <= a.length;
int nRemaining = hi - lo;
// 这就简单了,如果数组长度小于2,肯定不需要排序了
if (nRemaining < 2)
return; // Arrays of size 0 and 1 are always sorted
// 经过java的不断调试,发现数组长度如果小于32,使用二分排序插入排序更快
// 所以首先我们研究的是二分插入排序
if (nRemaining < MIN_MERGE) {
int initRunLen = countRunAndMakeAscending(a, lo, hi);
binarySort(a, lo, hi, lo + initRunLen);
return;
}
// 下面是第二种实现方式
......
}
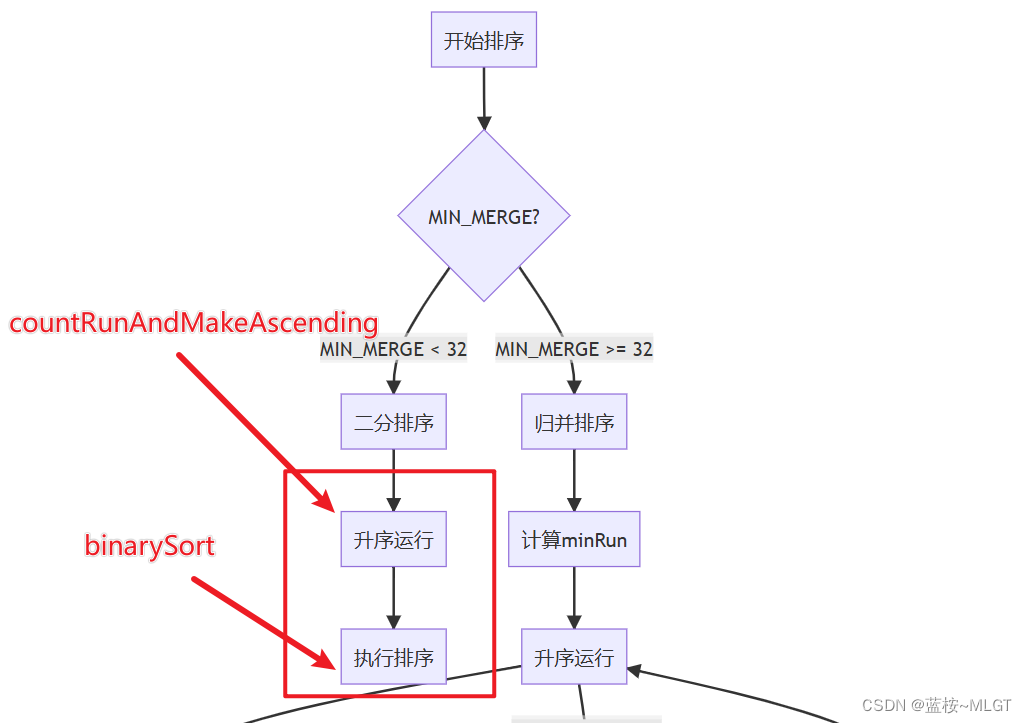
二分排序一共分为两步,第一步是升序运行(必须的步骤),第二步就是核心的排序算法,第一步的代码和讲解如下:
// 参数为数组和两个下标:起始0和长度
private static int countRunAndMakeAscending(Object[] a, int lo, int hi) {
assert lo < hi;
int runHi = lo + 1;
if (runHi == hi)
return 1;
// 下面这一步做了两件事情,第一件是寻找最小的升序子数组,假设数组为[2, 1, 4, 5, 6]
// 那返回的就是2,因为这个数组的第一个元素比第二个元素大,必须要寻找一个长度最短的升序数组
// 这里找到的就是数组[1, 2],返回的就是这个数组的长度2
// 第二件事情就是给排序的数组进行第一步排序,排序的范围就是上面寻找的最小升序数组的长度
// 一定要进行这个排序,这是二分排序的出发点,如果没有这一步下面的核心排序将无法完成
// 那么最终返回的数组就是[1, 2, 4, 5, 6]
if (((Comparable) a[runHi++]).compareTo(a[lo]) < 0) { // 检测到第二个元素比第一个小(降序)
while (runHi < hi && ((Comparable) a[runHi]).compareTo(a[runHi - 1]) < 0)
runHi++;
// 对指定范围排序的方法,这里就是反转那部分数组
reverseRange(a, lo, runHi);
} else { // 相反,最开始有升序的数组
while (runHi < hi && ((Comparable) a[runHi]).compareTo(a[runHi - 1]) >= 0)
runHi++;
}
return runHi - lo;
}
上面一直强调说要一定要找到数组中的最小升序子数组并排序,可能不太明白为啥吧,看下面这张二分排序的图可能就理解了。

这就相当于给了一个台阶,一个起始点,因为二分排序都是在前面的元素找合适自己的位置,所以起码排序的数组要有一个简单的升序小数组,不然你第一个元素前面也没有东西啊是不是,无论从逻辑还是代码上都是不可行的,所以这一步是非常有必要的,如果还不理解到排序的时候就又知道了。
来吧,核心的第二步,温馨提示,下面的代码研究了稍微长的时间,别看就这么一点,也是debug源码了很长时间才理解的,建议还是看完后在源码中进行debug,对应看就可以很快理解。
// 参数:a为排序的数组,lo为0(起始下标),hi为数组长度,start为排序的起始下标
// start就是上面那一步寻找的最小升序子数组的长度
private static void binarySort(Object[] a, int lo, int hi, int start) {
// 断言,一般用在指定范围排序时,如果不指定范围肯定不会出错
assert lo <= start && start <= hi;
if (start == lo)
start++;
// 源码中常见的for循环写法
for ( ; start < hi; start++) {
// 类型转换为Comparable ,用compare方法比较
Comparable pivot = (Comparable) a[start];
// 这里的left可以理解为排序范围的最左边下标,一般都是0
// right就是排序范围最右边下标,根据循环不断+1
// left和right就是排序的元素需要再前面寻找合适范围时的数组范围,可以根据图片在理解一下
int left = lo;
int right = start;
assert left <= right;
// 这一步就是判断start之前的数组需要整体移动还是部分移动
// 整体移动就是start下标的元素放在了最前面
// 部分移动就是start下标的元素放在了中间
while (left < right) {
// 移位运算,和最开始说的二分查找有联动,先找前面最中间的元素比较
// 如果比中间的元素大,则继续向上的,减少判断次数
int mid = (left + right) >>> 1;
if (pivot.compareTo(a[mid]) < 0)
right = mid;
else
left = mid + 1;
}
assert left == right;
// 这里的n是判断数组要怎样移动,有三种移动方式
// 当n为2,需要进行三次交换,这三次交换是将排序的元素放在中间的某个位置了
// 当n为1,需要进行两次交换,依旧是放在了中间的某个位置
int n = start - left; // The number of elements to move
switch (n) {
case 2: a[left + 2] = a[left + 1];
case 1: a[left + 1] = a[left];
break;
// 这一步是n可能不是1和2,表示排序的元素需要移动到最前面
// 这时候就将数组排序范围内除第一个元素外,整体向后挪动
// 例如[2, 3, 4, 1],将1移动到最前面,这一步就是将数组变为了[2, 2, 3, 4]
// 下面那一步将第一个元素赋值为1,这一段排序完成
// 也有可能排序的位置比前面元素都大,这时候的复制操作相当于没有移动
default: System.arraycopy(a, left, a, left + 1, n);
}
// 这一步必须,如果是正常的顺序如[1, 2, 3],也是将3换为了3
// 相反则是将排序的元素放到应该的位置
a[left] = pivot;
}
}
上面最难懂的可能就是那个while循环和switch了,如果要快速理解这两段代码你需要正确理解二分查询的思路,又回到了我们说第一步要找一个有序的子数组,就是为了二分查询做准备,每次都对半比较,非常节省时间,而switch中的2和1其实就是看怎么你在哪个范围进行数组交换,想一想,上面的while循环是二分查找无非就是两种结果,你比前面的都大,要么在前面的某个元素后面,那么这个后面又可以分为两种情况,一种是正好在中间,你需要移动其它两个元素,一种是在边界,你移动一个元素就好,有的人可能又疑惑,为啥只有1和2两种,好理解也不好理解,相当于你插队要么在最前面和最后面,要么在中间,只有这两种可能吧,别说你要骑在人家头上哈。
二分排序为啥快呢?如果从移动的次数来讲,都是一样的,咋滴你都得移动那么多次,无论是哪种排序,效率只能体现了时间复杂度上了,二分排序就是降低了时间复杂度,为
l
o
g
n
logn
logn,包括上面的复制数组,就是整体移动的操作,比你一个一个移动快吧,现在知道为啥说这个效率高了吧。
归并排序:
这里实现的思路和代码都比较复杂,我这里简单分析一下步骤,如果要完全搞懂里面的所有实现方式还是比较费劲的,如果对算法很感兴趣可以看一下具体的实现步骤,里面包含了太多算法的知识。
ComparableTimSort ts = new ComparableTimSort(a, work, workBase, workLen);
// 计算最小的运行长度,也就是看分割数组的长度最小是多少合适
// 因为当数组长度达到一定程度时,使用二分排序较快,这也是这个步骤的作用
int minRun = minRunLength(nRemaining);
do {
// 为二分排序做准备
int runLen = countRunAndMakeAscending(a, lo, hi);
// 如果达到二分排序的条件,进行二分排序
if (runLen < minRun) {
int force = nRemaining <= minRun ? nRemaining : minRun;
binarySort(a, lo, lo + force, lo + runLen);
runLen = force;
}
// 将分割的排序数组压入栈
ts.pushRun(lo, runLen);
// 合并相邻的两个排序数组
ts.mergeCollapse();
// Advance to find next run
lo += runLen;
nRemaining -= runLen;
} while (nRemaining != 0);
assert lo == hi;
// 整体合并所有的排序数组为1个
ts.mergeForceCollapse();
assert ts.stackSize == 1;
世界上最快的排序算法-Timsort
想要深入了解的可以看上面那篇博客,其中对核心步骤进行了讲解。
5. 数组查询(binarySearch二分查找)
二分查找看到这已经不陌生了吧,我们直接上代码。
有很多重载方法,最终实现的核心方法为binarySearch0,同样有指定范围查找和全部查询。
private static int binarySearch0(Object[] a, int fromIndex, int toIndex,
Object key) {
int low = fromIndex;
int high = toIndex - 1;
while (low <= high) {
// 移位运算,对半砍下标
int mid = (low + high) >>> 1;
@SuppressWarnings("rawtypes")
// 类型转换为comparable
Comparable midVal = (Comparable)a[mid];
@SuppressWarnings("unchecked")
// 需要比较的元素和中间的元素比较
int cmp = midVal.compareTo(key);
// 如果中间元素小,则在上半部分寻找,low限定下标范围为上半部分
if (cmp < 0)
low = mid + 1;
// 相反则为下半部分
else if (cmp > 0)
high = mid - 1;
// 找到了,返回下标
else
return mid; // key found
}
// 没找到
return -(low + 1); // key not found.
}
6. 数组转Stream流(Arrays.stream)
Stream流作为jdk1.8的新特性是非常受欢迎的,Arrays工具类也提供了将数组转为流进行操作的接口,具体如下:
Set<Integer> arr = Arrays.stream(array).collect(Collectors.toSet());
System.out.println("arr = " + arr);
其实来说就是提供更加方便的操作,让我们能对数组也进行流的操作,毕竟数组是无法直接转为流的,转为流其实你就可以为所欲为了,比如我们常见的去重操作,查询,过滤,统计,分组等等都可以使用,非常方便。
7. 数组打印(Arrays.deepToString)
这个方法是我们开发中打印到控制台的一个接口,不同的是可以完美的数组元素,如果直接打印会是数组的内存地址,之前都是for循环打印的,这个接口给我们提供了便利。
因为底层实现太长,而且思路也很简单,就是使用StringBuilder进行了元素的拼接,之后调用toString方法打印到控制台,只不过需要注意的是,如果是对象数组,需要重写对象的toString方法,不然打印的还是对象的内存地址。
8. 数组填充(setAll和parallelPrefix)
最开始我们说过fill方法可以填充数组,但前提是会填充相同的元素,而这两个方法使用函数式编程可以更灵活的填充我们想要的元素。我们只需要了解怎么使用即可,具体底层想要了解函数式编程的可以看看,关于函数式编程,后期会专门出一篇。
int[] arr = new int[] { 1, 2, 3, 4};
Arrays.parallelPrefix(arr, (left, right) -> left + right);
// [1, 3, 6, 10]
System.out.println(Arrays.toString(arr));
这里简单演示了一下对数组元素相邻元素相加,当然还有很多用法,具体就要看你的业务需求了。
总结
总体来说还是涉及了很多的底层知识,其中最难得莫过于归并排序和二分排序了,当然这也是我们不断提高自己的方式,总要挑战难点吧,不然怎么强大呢。
下期预告
下一篇博客我们将围绕集合中的Set家族进行讲解,期待下次见面。





![[DDR4] DDR 简史](https://img-blog.csdnimg.cn/direct/8d31fad7a28745eb81e253606f226423.png#pic_center)