转载请注明出处: https://blog.csdn.net/weixin_44013533/article/details/139701843
作者:CSDN@|Ringleader|
目录
- 目标
- 数学理论
- 资源准备
- 数据准备
- 代码实现
- Unity准备
- 效果展示
- 注意事项
- 后记
目标
目标:利用Unity的物理引擎实现 “日地月三体系统” 。
效果类似下面的示意图:

数学理论
- 万有引力公式
- 向心力公式
- 天体圆周运动轨道速度公式

资源准备
日月地模型及贴图:
https://assetstore.unity.com/packages/3d/environments/planets-of-the-solar-system-3d-90219

数据准备
| 名称 | 数值 |
|---|---|
| 引力常数 ( G ) | G = 6.67430 × 1 0 − 11 m 3 kg − 1 s − 2 G = 6.67430 \times 10^{-11} \, \text{m}^3 \, \text{kg}^{-1} \, \text{s}^{-2} G=6.67430×10−11m3kg−1s−2 |
| 太阳半径 R Sun R_{\text{Sun}} RSun | R Sun = 6.96 × 1 0 8 m R_{\text{Sun}} = 6.96 \times 10^8 \, \text{m} RSun=6.96×108m |
| 太阳质量 M Sun M_{\text{Sun}} MSun | M Sun = 1.989 × 1 0 30 kg M_{\text{Sun}} = 1.989 \times 10^{30} \, \text{kg} MSun=1.989×1030kg |
| 日地距离 r Sun-Earth r_{\text{Sun-Earth}} rSun-Earth | r Sun-Earth = 1.496 × 1 0 11 m r_{\text{Sun-Earth}} = 1.496 \times 10^{11} \, \text{m} rSun-Earth=1.496×1011m |
| 地球半径 R Earth R_{\text{Earth}} REarth | R Earth = 6.371 × 1 0 6 m R_{\text{Earth}} = 6.371 \times 10^6 \, \text{m} REarth=6.371×106m |
| 地球质量 M Earth M_{\text{Earth}} MEarth | M Earth = 5.972 × 1 0 24 kg M_{\text{Earth}} = 5.972 \times 10^{24} \, \text{kg} MEarth=5.972×1024kg |
| 地月距离 r Earth-Moon r_{\text{Earth-Moon}} rEarth-Moon | r Earth-Moon = 3.844 × 1 0 8 m r_{\text{Earth-Moon}} = 3.844 \times 10^8 \, \text{m} rEarth-Moon=3.844×108m |
| 月球半径 R Moon R_{\text{Moon}} RMoon | R Moon = 1.7371 × 1 0 6 m R_{\text{Moon}} = 1.7371 \times 10^6 \, \text{m} RMoon=1.7371×106m |
| 月球质量 M Moon M_{\text{Moon}} MMoon | M Moon = 7.348 × 1 0 22 kg M_{\text{Moon}} = 7.348 \times 10^{22} \, \text{kg} MMoon=7.348×1022kg |
当然不能取这么大,缩放下比例尺后的数据如下,同时用这些数据初始化系统。
public class ConstantParamter : MonoBehaviour
{
public static float gravitationalConstant = 0.6674f; // 原6.674e-11
public static float sunMass = 1.989e6f; //缩小10^24倍,原1.989e30
public static float earthMass = 5.972f; //原5.972e24
public static float moonMass = 0.07348f; //原7.348e22
public static float distanceOfSunAndEarth = 1496f; //缩小10^8倍,原1.496e11
public static float distanceOfEarthAndMoon = 3.844f; //原3.844e8
public static float sunScale = 6.96f;
public static float earthScale = 0.06371f;
public static float moonScale = 0.017371f;
public static float earthTangentialVelocityScale = 1.4f; //1.45是近似标准圆
public static float moonTangentialVelocityScale = 1f; //1.45是近似标准圆
public Rigidbody sun;
public Rigidbody earth;
public Rigidbody moon;
private void Start()
{
// 初始化太阳
sun.mass = sunMass;
sun.position = Vector3.zero;
// 初始化地球
earth.mass = earthMass;
earth.position = new Vector3(distanceOfSunAndEarth, 0, 0);
// var earthScale = ConstantParamter.earthScale;
// earth.transform.localScale = new Vector3(earthScale, earthScale, earthScale);
//初始化月球 (月球位置在日地之间还是外面不影响)
moon.mass = moonMass;
moon.position = new Vector3(distanceOfSunAndEarth - distanceOfEarthAndMoon, 0, 0);
// var moonScale = ConstantParamter.moonScale;
// moon.transform.localScale = new Vector3(moonScale, moonScale, moonScale);
}
}
scale 和初始位置最好能自己调整,方便后面的collider范围确定。
代码实现
-
UniversalGravity万有引力脚本,对进入trigger的物体施加指向自己的万有引力public class UniversalGravity : MonoBehaviour { private float gravitationalConstant = ConstantParamter.gravitationalConstant; public Rigidbody center; private int moonLayer; private int earthLayer; private int sunLayer; public bool printMsg = false; private void Start() { moonLayer = LayerMask.NameToLayer("moon"); earthLayer = LayerMask.NameToLayer("earth"); sunLayer = LayerMask.NameToLayer("sun"); } private void OnTriggerStay(Collider other) { try { Print(other.name+"进入"+this.name+"引力场触发器"); var layer = other.gameObject.layer; if (layer.Equals(moonLayer) || layer.Equals(earthLayer)) { var otherAttachedRigidbody = other.attachedRigidbody; var gravityDirection = center.transform.position - other.transform.position ; var gravityForce = gravitationalConstant * center.mass * otherAttachedRigidbody.mass / Mathf.Pow(gravityDirection.magnitude, 2); otherAttachedRigidbody.AddForce(gravityDirection.normalized * gravityForce); var msg = $"{other.name}被{center.name}施以{gravityDirection.normalized * gravityForce}的引力。"; Print(msg); } } catch (Exception e) { Print(other.name+"异常:"+e); throw; } } void Print(string msg) { if (printMsg) { Debug.Log(msg); } } } -
EarthTangentialVelocity:计算地球绕日运动的初速度,因为轨道可能是椭圆,所以在标准圆轨道速度基础上乘以个缩放值// 计算地球绕日运动的初速度,因为轨道可能是椭圆,所以在标准圆轨道速度基础上乘以个缩放值 public class EarthTangentialVelocity : MonoBehaviour { private float gravitationalConstant = ConstantParamter.gravitationalConstant; private float earthTangentialVelocityScale = ConstantParamter.earthTangentialVelocityScale; public Rigidbody sun; Rigidbody rig; private void Start() { rig = GetComponent<Rigidbody>(); rig.velocity = CalculateVelocity(rig, sun, earthTangentialVelocityScale); print(name + "的初始速度为:" + rig.velocity); } private Vector3 CalculateVelocity(Rigidbody rigid, Rigidbody center, float tangentialVelocityScale) { Vector3 startPosition = rigid.position; var distance = startPosition - center.position; var tangentialDirection = Vector3.Cross(distance, Vector3.up).normalized; Vector3 tangentialVelocity = tangentialDirection * Mathf.Sqrt(gravitationalConstant * center.mass / distance.magnitude) * tangentialVelocityScale; return tangentialVelocity; } } -
MoonTangentialVelocity:计算月球初始切向速度。// 计算月球初始切向速度。 // 把月亮起源当作地球抛落物,所以月球初始速度=地球绕日标准圆速度+月球绕地标准圆速度 // 当然由于轨道不一定是标准圆,所以会加一个缩放值 public class MoonTangentialVelocity : MonoBehaviour { private float gravitationalConstant = ConstantParamter.gravitationalConstant; private float earthTangentialVelocityScale = ConstantParamter.earthTangentialVelocityScale; private float moonTangentialVelocityScale = ConstantParamter.moonTangentialVelocityScale; public Rigidbody sun; public Rigidbody earth; Rigidbody rig; private void Start() { rig = GetComponent<Rigidbody>(); var tangentialVelocity1 = CalculateVelocity(rig, earth, moonTangentialVelocityScale); var tangentialVelocity2 = CalculateVelocity(earth, sun, earthTangentialVelocityScale); rig.velocity = tangentialVelocity1 + tangentialVelocity2; print(name + "的初始速度为:" + rig.velocity); } private Vector3 CalculateVelocity(Rigidbody rigid, Rigidbody center, float tangentialVelocityScale) { Vector3 startPosition = rigid.position; var distance = startPosition - center.position; var tangentialDirection = Vector3.Cross(distance, Vector3.up).normalized; Vector3 tangentialVelocity = tangentialDirection * Mathf.Sqrt(gravitationalConstant * center.mass / distance.magnitude) * tangentialVelocityScale; return tangentialVelocity; } }
Unity准备
- 本系统使用Unity的built-in physics,将上面store下载的日月地三体模型prefab拖入场景中,各自新增三个万有引力碰撞体,设为isTrigger并调整大小,分别拖入
UniversalGravity脚本并添加引力中心。

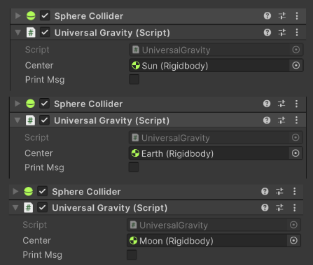
- 为earth和moon分别添加
EarthTangentialVelocity、MoonTangentialVelocity脚本,这两个脚本是为地球和月球提供初始切向速度, 以保证它们能绕太阳做圆周运动。 - 使用trail组件即可展示地月运行轨迹
- moon和earth添加对应的layer,注意对应的trigger也要添加layer,过滤不需要施加力的对象。
效果展示
(紫色为月球轨迹,绿色为地球轨迹)
unity物理引擎实现简单日地月三体系统

地月交会瞬间

完整地月绕日轨道
注意事项
-
一定要考虑月球对地球的引力,这是月球不会脱离地球的主要原因
如果不考虑月球对地球的引力,那么在离心力的作用下月球将会逐渐远离太阳,当然也可能像彗星一样绕超长轨道绕日运动。(就像旋转的雨伞,水滴脱离伞面后将会远远地抛离)实验效果:

当没有月球对地球引力作用时,月球绕日轨道(类似彗星轨道)
我一开始就是因为没考虑月球引力作用,总是得不到正确的轨道,还以为是比例尺导致的,不断调整日地引力常数,缩放月地切线速度,一直没成功,直到考虑到月球引力作用,才瞬间豁然开朗。
-
月球初速一定是在地球绕日初速的基础上进行增减的。也就是我代码中提到的 “月球是地球抛落物” 基于这个假说进行的(二体同源)。
当然也可以采用 “捕获说” ,但实验下来会发现,月球的初速对实验结果影响很大,月球轨道很容易变成或大或小的椭圆。

月球和地球速度不能差异过大,此图为月球速度过大,导致轨道为大椭圆

月球和地球速度不能差异过大,此图为月球速度过小,导致轨道为小椭圆
-
月球不应作为地球的子对象。第一rigidbody会忽略层级关系,也就是说地球不会带动月球移动;第二也不应该用非物理系统的思想模拟地月系统。
- 一开始就是因为我得不到正常的月绕地轨道,所以尝试了用transform更新月球和fixJoint 来绑定月球,但觉得这种方式很不物理,所以折腾了几个小时参数,才突然考虑到上面第一条问题。
-
本文只是实现了简单的日地月系统,没有精确确定地球月球公转周期,自转也没考虑,如果详细实现的话,就可以做成类似下面链接中所展示的太阳系模型了。
太阳系模型
后记
经过上面的实验,基本实现了简单的日地月三体系统。还是相当好玩的。至于月球对地球引力是不是实验中所展示的那样重要,可能还需要更多理论学习才能明白。
延申阅读
- 太阳对月球的引力比地球大两倍多,为什么月球没有被太阳吸过去?
- 太阳对月球的引力是地球2.2倍,为啥月亮没被太阳抢走?
当然未来有时间的话,还会尝试其他天体系统,比如三体运动。

三体问题
物理系统的话不久将会更新,内容还是比较多的,本节因为比较简短独立且比较好玩,所以独立成章了。
![【2024最新华为OD-C/D卷试题汇总】[支持在线评测] URL拼接(100分) - 三语言AC题解(Python/Java/Cpp)](https://img-blog.csdnimg.cn/direct/c1b7a8418ef34a48b018f2cb7fb89101.png)