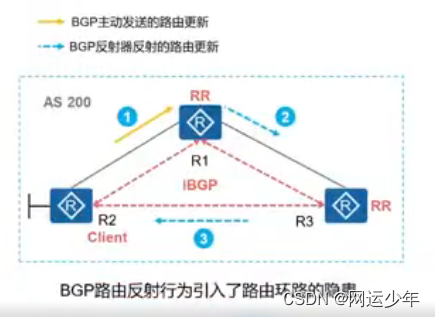
前言

题解
A. 最少胜利题数
签到
n1 = len(set(input()))
n2 = len(set(input()))
if n1 < n2:
n1, n2 = n2, n1
print (-1 if n1 == 6 else n1 - n2 + 1)
B. 最少操作次数
思路: 分类讨论
只有-1,0,1,2这四种结果
特判 0+1+, 1+0+
n = int(input())
s = input()
# 枚举
from collections import Counter
cnt = Counter(s)
if cnt['0'] == cnt['1']:
if s[0:(n//2)] == "0" * (n//2) or s[0:(n//2)] == "1" * (n//2):
print (-1)
else:
print (2)
elif cnt['0'] == n or cnt['1'] == n:
print (0)
else:
print (1)
C. 最多数组数量
思路: 双指针
枚举第一个和第二个数组的分割点x
然后找第二个和第三个数组的分割点y
找到y点后,往右移动的点都满足需求
很典的题,应该还有其他的解法
n = int(input())
arr = list(map(int, input().split()))
# 双指针
res = 0
j = 0
s1, s2 = 0, 0
s = sum(arr)
for i in range(n - 2):
s1 += arr[i]
while j <= i:
s2 += arr[j]
j += 1
while (j < n and (s2 - s1 <= s1 or s2 - s1 <= s - s1 - (s2 - s1))):
s2 += arr[j]
j += 1
if j < n:
res += (n - j)
print (res)
D. 最小连通代价
思路: 分类讨论
非常好的一道题,分别讨论ab的正负
因为要尽量小,所以负值为完全图,正值维护最简单的树结构
- 完全图
- 树形图
ab都为正数时,其大小关系也需要在讨论下
t = int(input())
def solve():
n, a, b = list(map(int, input().split()))
arr = list(map(int, input().split()))
n1 = sum([1 for v in arr if v % 2 == 0])
n2 = sum([1 for v in arr if v % 2 != 0])
res = 0
if a <= 0 and b <= 0:
res += n1 * (n1 - 1) // 2 * a
res += n2 * (n2 - 1) // 2 * a
res += n1 * n2 * b
elif a <= 0:
res += n1 * (n1 - 1) // 2 * a
res += n2 * (n2 - 1) // 2 * a
if n1 > 0 and n2 > 0:
res += b
elif b <= 0:
if n1 > 0 and n2 > 0:
res = n1 * n2 * b
elif n1 > 0:
res = (n1 - 1) * a
elif n2 > 0:
res = (n2 - 1) * a
else:
if b <= a:
if n1 > 0 and n2 > 0:
res = (n1 + n2 - 1) * b
elif n1 > 0:
res = (n1 - 1) * a
elif n2 > 0:
res = (n2 - 1) * a
else:
if n1 > 0:
res += (n1 - 1) * a
if n2 > 0:
res += (n2 - 1) * a
if n1 > 0 and n2 > 0:
res += b
print (res)
for _ in range(t):
solve()
E. 最大稳定数值
思路: 树上DFS + 名次树(离散化+数状数组/动态开点的线段树)
对于某个节点,祖先的前缀和不会变,但是子孙的和会变小
根据定义,节点会因为子树的删边而成为满足要求
这些点具备如下特点
- 祖先节点前缀和大于等于该节点
- 该节点大于子树节点和
可以称这些节点为候选节点
然后从删边寻求突破口
删边会影响祖先节点集的子树和,能否快速统计影响个数呢? 删边会影响祖先节点集的子树和,能否快速统计影响个数呢? 删边会影响祖先节点集的子树和,能否快速统计影响个数呢?
或者说挪动某个范围,统计满足条件的个数 或者说挪动某个范围,统计满足条件的个数 或者说挪动某个范围,统计满足条件的个数
这种一般采用,名次树/树状数组/线段树来快速计算
所以大致的思路为
- 自底向上DFS,统计子树和和祖先前缀和
- 自顶向下DFS,利用名次树统计变更节点数
这样两次DFS即可,时间复杂度为 O ( n ) O(n) O(n)
import java.io.BufferedInputStream;
import java.util.*;
public class Main {
static class BIT {
int n;
int[] arr;
public BIT(int n) {
this.n = n;
this.arr = new int[n + 1];
}
int query(int p) {
int res = 0;
while (p > 0) {
res += arr[p];
p -= p & -p;
}
return res;
}
void update(int p, int d) {
while (p <= n) {
this.arr[p] += d;
p += p & -p;
}
}
}
static
public class Solution {
int n;
int[] arr;
List<Integer>[]g;
long[] up;
long[] down;
int[] cs;
Map<Long, Integer> idMap = new HashMap<>();
BIT bit;
public int solve(int n, int[] arr, int[] pa) {
this.n = n;
this.arr = arr;
this.up = new long[n];
this.down = new long[n];
this.cs = new int[n];
this.g = new List[n];
Arrays.setAll(g, x->new ArrayList<>());
for (int i = 0; i < n; i++) {
if (pa[i] != -1) {
g[pa[i]].add(i);
}
}
dfs(0, -1, 0);
TreeSet<Long> ids = new TreeSet<>();
for (int i = 0; i < n; i++) {
if (up[i] - arr[i] >= arr[i] && down[i] - arr[i] > arr[i]) {
ids.add(down[i] - 2l * arr[i]);
}
ids.add(down[i]);
}
int ptr = 1;
for (long k: ids) {
idMap.put(k, ptr++);
}
this.bit = new BIT(ids.size());
dfs3(0, -1);
return gAns + cs[0];
}
int gAns = 0;
void dfs3(int u, int fa) {
int idx = idMap.get(down[u]);
int r = bit.query(idx);
r -= cs[u];
if (r > gAns) {
gAns = r;
}
if (up[u] - arr[u] >= arr[u] && down[u] - arr[u] > arr[u]) {
bit.update(idMap.get(down[u] - arr[u] * 2l), 1);
}
for (int v: g[u]) {
if (v == fa) continue;
dfs3(v, u);
}
if (up[u] - arr[u] >= arr[u] && down[u] - arr[u] > arr[u]) {
bit.update(idMap.get(down[u] - arr[u] * 2l), -1);
}
}
void dfs(int u, int fa, long pre) {
up[u] = pre + arr[u];
down[u] += arr[u];
for (int v: g[u]) {
if (v == fa) continue;
dfs(v, u, up[u]);
down[u] += down[v];
cs[u] += cs[v];
}
if (up[u] - arr[u] >= arr[u] && down[u] - arr[u] <= arr[u]) {
cs[u] += 1;
}
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(new BufferedInputStream(System.in));
int n = sc.nextInt();
int[] arr = new int[n];
for (int i = 0; i < n; i++) {
arr[i] = sc.nextInt();
}
int[] pa = new int[n];
for (int i = 0; i < n; i++) {
pa[i] = sc.nextInt() - 1;
}
Solution solution =new Solution();
System.out.println(solution.solve(n, arr, pa));
}
}
F. 最少逆序对数
这题的思路可以分为两层
- 求一个固定长度的数组,其逆序对最小为多少
- 如何解决数组递增的问题
先来解决第一个问题
前置准备,令
f
(
a
i
)
为数组中大于
a
i
的个数
f(a_i)为数组中大于a_i的个数
f(ai)为数组中大于ai的个数
g
(
a
i
)
为数组中小于
a
i
的个数
g(a_i)为数组中小于a_i的个数
g(ai)为数组中小于ai的个数
在一个数组中arr,移动一次的代价为

h ( a 0 ) = f ( a 0 ) − g ( a 0 ) h(a_0) = f(a_0) - g(a_0) h(a0)=f(a0)−g(a0)
显然这题等价转换后,找到一个j,使得
S ( a ) = m i n ∑ i = 0 i = j h ( a i ) , 0 ≤ j < n S(a) = min \sum_{i=0}^{i=j} h(a_i), 0\le j \lt n S(a)=mini=0∑i=jh(ai),0≤j<n
那这题的难点就在于,
如何快速的求解 f ( a i ) , g ( a i ) 如何快速的求解f(a_i), g(a_i) 如何快速的求解f(ai),g(ai)
引入迭代的思维
假设 a r r [ 0 : i ] 子数组,其每个元素的 f i ( a j ) , g i ( a j ) 已维护,那尾巴新增一个元素 a r r [ i + 1 ] ,此时会变化什么呢? arr[0:i]子数组,其每个元素的f_i(a_j), g_i(a_j)已维护,那尾巴新增一个元素arr[i+1],此时会变化什么呢? arr[0:i]子数组,其每个元素的fi(aj),gi(aj)已维护,那尾巴新增一个元素arr[i+1],此时会变化什么呢?,
f i + 1 ( a j ) , g i + 1 ( a j ) 的更新只需要 O ( 1 ) 代价 f_{i+1}(a_j), g_{i+1}(a_j)的更新只需要O(1)代价 fi+1(aj),gi+1(aj)的更新只需要O(1)代价
进而 a r r [ 0 : i + 1 ] 的 h i + 1 序列重建,只需要 O ( n ) 的代价 进而{arr[0:i+1]的h_{i+1}序列重建,只需要O(n)的代价} 进而arr[0:i+1]的hi+1序列重建,只需要O(n)的代价
a r r [ 0 : i + 1 ] 的最小逆序也可以 O ( n ) 求解 arr[0:i+1]的最小逆序也可以O(n)求解 arr[0:i+1]的最小逆序也可以O(n)求解
这样n长度的数组,只需要 O ( n 2 ) O(n^2) O(n2)求解得最终的解
如果这题,改为在线查询,可能会更难
n = int(input())
arr = list(map(int, input().split()))
f = [0] * n
g = [0] * n
acc = 0
res = []
for i in range(n):
for j in range(i - 1, -1, -1):
if arr[j] < arr[i]:
f[j] += 1
g[i] += 1
elif arr[j] > arr[i]:
g[j] += 1
f[i] += 1
acc += f[i]
ans = acc
tmp = 0
for j in range(i):
tmp = tmp + f[j] - g[j]
ans = min(ans, acc + tmp)
res.append(ans)
print (*res)
写在最后