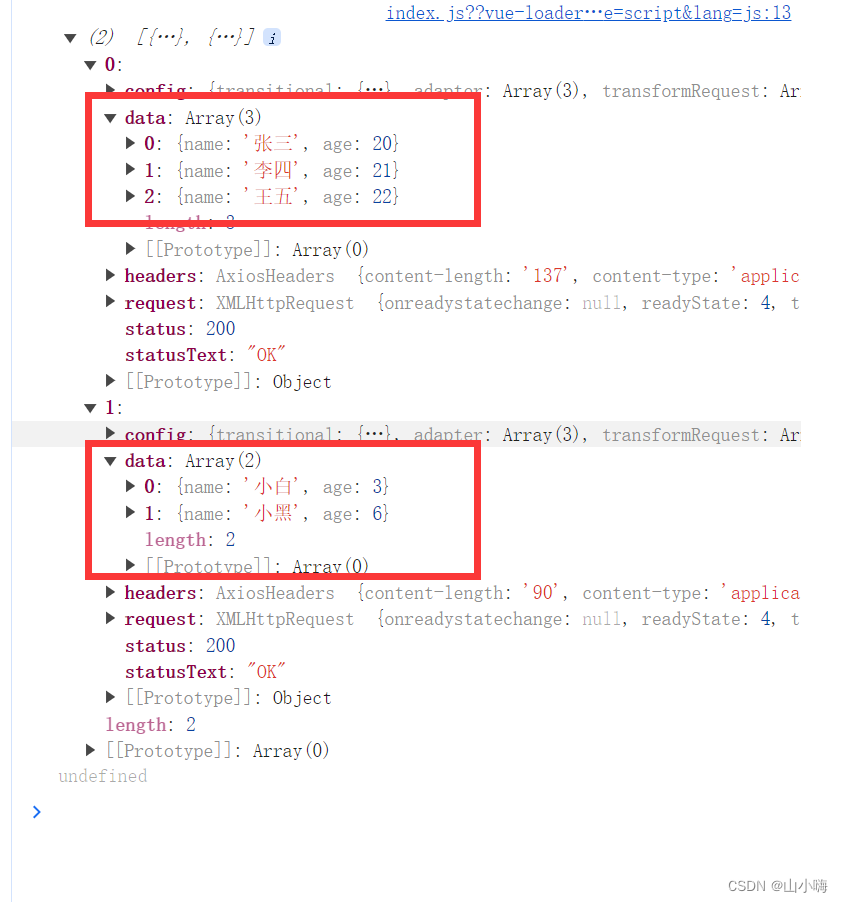
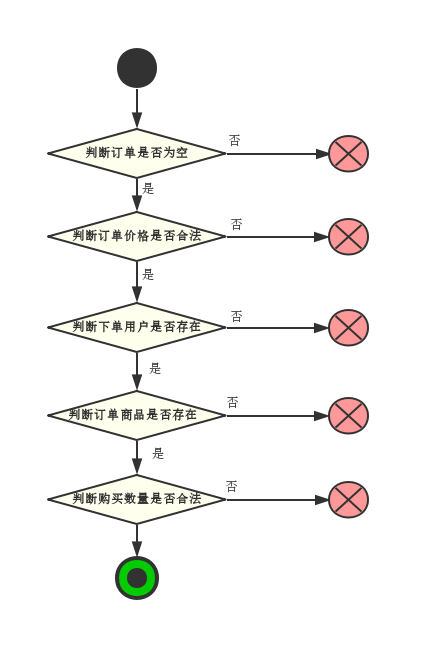
1. 建立 QP 模型:
1.1 车辆模型:
注:使用车辆横向动力学模型 + 纵向动力学模型(误差模型)

1.2 QP 问题模型:
注:详细推导见 笔记100:使用 OSQP-Eigen 对 MPC 进行求解的方法与代码-CSDN博客 中对【线性系统 + 线性约束】问题的 QP 问题的构建过程;
- 构建代价函数:

- 构建约束:

注1:其中
注2:其中 ,因为本身车辆模型提供的状态空间方程的状态量 x 就是误差量,对于误差量而言他的目标值就是0;
a
a
a
a
a
2. 代码实现
- 头文件 common.h :定义各种结构体
#include <fstream>
#include <iostream>
#include <string>
#include <lgsvl_msgs/VehicleControlData.h>
#include <nav_msgs/Odometry.h>
#include <std_msgs/Header.h>
#include <sensor_msgs/Imu.h>
#include "map.h"
#include "reference_line.h"
#include "ros/ros.h"
#include "tf/tf.h"
// 车辆状态信息
struct VehicleState {
double x; // 车辆在【全局坐标系】中的 -- x值
double y; // 车辆在【全局坐标系】中的 -- y值
double heading; // 车辆在【全局坐标系】中的 -- 车辆朝向(车辆横摆角/航向角,也即车辆欧拉角中的偏航角 yaw)
double kappa; // 车辆在【全局坐标系】中的 -- 曲率(转弯半径的倒数)
double velocity; // 车辆在【全局坐标系】中的 -- 线速度
double angular_velocity; // 车辆在【全局坐标系】中的 -- 角速度(横摆角变化率)
double acceleration; // 车辆在【全局坐标系】中的 -- 加速度
double vx; // 速度在【车身坐标系的x轴】上的分量
double vy; // 速度在【车身坐标系的y轴】上的分量
double vz; // 速度在【车身坐标系的z轴】上的分量
double pitch; // 欧拉角 -- 在【车身坐标系】绕x轴转角 -- 俯仰角
double yaw; // 欧拉角 -- 在【车身坐标系】绕y轴转角 -- 偏航角
double roll; // 欧拉角 -- 在【车身坐标系】绕z轴转角 -- 横滚角
double target_curv; // 期望点的曲率
// 起点处车辆的信息
double planning_init_x; // 车辆起点在【全局坐标系】中的 -- x值
double planning_init_y; // 车辆起点在【全局坐标系】中的 -- y值
// added
double start_point_x;
double start_point_y;
double relative_x = 0;
double relative_y = 0;
double relative_distance = 0;
double last_velocity = 0; // 上一个时间步的 -- 车辆线速度
double last_v_err = 0; // 上一个时间步的 -- 车辆线速度误差
double last_v_time = 0; // 上一个时间步的 -- 速度时间戳
double last_acc = 0; // 上一个时间步的 -- 加速度
double cur_v_err = 0; // 当前时间步的 -- 速度误差
double cur_v_time = 0; // 当前时间步的 -- 速度时间戳
double cur_acc = 0; // 当前时间步的 -- 加速度
};
// 轨迹(目标)点
struct TrajectoryPoint {
double x; // 目标点在【全局坐标系】中的 -- x值
double y; // 目标点在【全局坐标系】中的 -- y值
double heading; // 目标点在【全局坐标系】中的 -- 目标点处的切线与全局坐标系的x轴之间的夹角(目标航向角)
double kappa; // 目标点在【全局坐标系】中的 -- 目标点处的曲率
double v; // 目标点在【全局坐标系】中变化的 -- 速度
double a; // 目标点在【全局坐标系】中变化的 -- 加速度
};
// 目标轨迹(vector容器中装有所有的路径点)
struct TrajectoryData {
std::vector<TrajectoryPoint> trajectory_points;
};
// 车辆横向动力学模型(误差型)中状态量x包含的4个分量
struct LateralControlError {
double lateral_error; // 横向误差
double heading_error; // 航向误差
double lateral_error_rate; // 横向误差变化率
double heading_error_rate; // 航向误差变化率
};
// 控制命令
struct ControlCmd {
double steer_target; //横向控制命令:方向盘转角
double acc; //总想控制命令:油门开度
};
typedef std::shared_ptr<LateralControlError> LateralControlErrorPtr;- 头文件 mpc_controller.h :定义车辆模型涉及到的所有矩阵和信息
#pragma once
#include <math.h>
#include <fstream>
#include <iomanip>
#include <memory>
#include <string>
#include "Eigen/Core"
#include "common.h"
#include "mpc_osqp.h"
namespace shenlan {
namespace control {
using Matrix = Eigen::MatrixXd;
class MPCController {
public:
MPCController();
~MPCController();
void LoadControlConf();
void Init();
bool ComputeControlCommand(const VehicleState &localization, const TrajectoryData &planning_published_trajectory, ControlCmd &cmd);
protected:
double Wheel2SteerPct(const double wheel_angle);
void UpdateState(const VehicleState &vehicle_state);
void UpdateMatrix(const VehicleState &vehicle_state);
// 计算横向误差(未定义)
void ComputeLateralErrors(const double x, const double y, const double theta, const double linear_v, const double angular_v, const double linear_a, LateralControlErrorPtr &lat_con_err);
// 计算纵向误差(未定义)
void ComputeLongitudinalErrors(const VehicleState &vehicle_state);
void ComputeErrors(const double x, const double y, const double theta, const double linear_v, const double angular_v, const double linear_a, LateralControlErrorPtr &lat_con_err);
void ToTrajectoryFrame(const double x, const double y, const double theta, const double v, const TrajectoryPoint &ref_point, double *ptr_s, double *ptr_s_dot, double *ptr_d, double *ptr_d_dot);
TrajectoryPoint QueryNearestPointByPosition(const double x, const double y);
// 全局规划路径中的所有点:
std::vector<TrajectoryPoint> trajectory_points_;
// 车辆的物理参数汇总:
double ts_ = 0.0; // 两个控制命令之间的时间间隔
double cf_ = 0.0; // 前轮侧偏刚度
double cr_ = 0.0; // 后轮侧偏刚度
double wheelbase_ = 0.0; // 车辆纵轴长度
double mass_ = 0.0; // 车辆总质量
double lf_ = 0.0; // 车辆纵轴中的lf
double lr_ = 0.0; // 车辆纵轴中的lr
double iz_ = 0.0; // 汽车的转动惯量
double steer_ratio_ = 0.0; // 方向盘的转角到轮胎转动角度之间的比值系数
Eigen::MatrixXd matrix_a_;
Eigen::MatrixXd matrix_a_coeff_;
Eigen::MatrixXd matrix_ad_;
Eigen::MatrixXd matrix_b_;
Eigen::MatrixXd matrix_bd_;
Eigen::MatrixXd matrix_state_;
Eigen::MatrixXd matrix_r_;
Eigen::MatrixXd matrix_q_;
Eigen::MatrixXd matrix_q_updated_;
const int basic_state_size_ = 6; // 状态量x的大小(横向误差 / 横向误差变化率 / 航向误差 / 航向误差变化率 / 纵向位置误差 / 纵向速度误差)
const int controls_ = 2; // 控制量u的大小(方向盘转角 / 汽车加速度)
double station_error_ = 0.0; // 纵向位置误差
double speed_error_ = 0.0; // 纵向速度误差
int mpc_max_iteration_ = 0; // MPC求解器的参数 -- QP求解器最大迭代次数
double mpc_eps_ = 0.0; // MPC求解器的参数 -- 计算阈值
const int horizon_ = 10; // MPC有限时域长度
double max_acceleration_ = 0.0; // 车辆最大加速度
double max_deceleration_ = 0.0; // 车辆最小加速度
double max_lat_acc_ = 0.0; // 转向时的最大横向加速度
double minimum_speed_protection_ = 0.1; // 车辆最小速度
double steer_single_direction_max_degree_ = 0.0; // 方向盘的最大转角
double wheel_single_direction_max_degree_ = 0.0; // 车轮的最大转角
};
} // namespace control
} // namespace shenlan- 源文件 mpc_controller.cpp :
#include "mpc_controller.h"
#include <algorithm>
#include <iomanip>
#include <utility>
#include <vector>
#include "Eigen/LU"
#include "math.h"
using namespace std;
namespace shenlan {
namespace control {
// 函数作用:构造函数
MPCController::MPCController() {}
// 函数作用:析构函数
MPCController::~MPCController() {}
// 函数作用:初始化车辆物理参数
void MPCController::LoadControlConf() {
ts_ = 0.01; // 两个控制命令之间的时间间隔
cf_ = 155493.663; // 前轮侧偏刚度
cr_ = 155493.663; // 后轮侧偏刚度
wheelbase_ = 1.0; // 车辆纵轴长度
max_acceleration_ = 0.8; // 车辆最大加速度 (总加速度)
max_deceleration_ = -0.8; // 车辆最小加速度 (总加速度)
max_lat_acc_ = 5.0; // 转向时的最大横向加速度 (横向加速度)
steer_ratio_ = 1.0; // 传动比
steer_single_direction_max_degree_ = 40.0; // 方向盘的最大转角(角度)
wheel_single_direction_max_degree_ = steer_single_direction_max_degree_ / steer_ratio_ / 180 * M_PI; // 车轮最大转角(弧度)
const double mass_fl = 55.0; // 左前悬的质量
const double mass_fr = 55.0; // 右前悬的质量
const double mass_rl = 65.0; // 左后悬的质量
const double mass_rr = 65.0; // 右后悬的质量
const double mass_front = mass_fl + mass_fr; // 前悬质量
const double mass_rear = mass_rl + mass_rr; // 后悬质量
mass_ = mass_front + mass_rear; // 总车质量
lf_ = wheelbase_ * (1.0 - mass_front / mass_); // 汽车前轮到中心点的距离
lr_ = wheelbase_ * (1.0 - mass_rear / mass_); // 汽车后轮到中心点的距离
iz_ = lf_ * lf_ * mass_front + lr_ * lr_ * mass_rear; // 汽车的转动惯量
mpc_eps_ = 0.01; // MPC求解器的参数 -- 计算阈值
mpc_max_iteration_ = 1500; // MPC求解器的参数 -- 最大迭代次数
return;
}
// 函数作用:初始化 -- 横向动力学模型中的矩阵 + 代价函数J中的矩阵
void MPCController::Init() {
LoadControlConf();
// 初始化(连续型)车辆横向动力学模型 -- 矩阵A
matrix_a_ = Matrix::Zero(basic_state_size_, basic_state_size_);
matrix_a_(0, 1) = 1.0;
matrix_a_(1, 2) = (cf_ + cr_) / mass_;
matrix_a_(2, 3) = 1.0;
matrix_a_(3, 2) = (lf_ * cf_ - lr_ * cr_) / iz_;
matrix_a_(4, 5) = 1;
matrix_a_(5, 5) = 0.0;
matrix_a_coeff_ = Matrix::Zero(basic_state_size_, basic_state_size_);
matrix_a_coeff_(1, 1) = -(cf_ + cr_) / mass_;
matrix_a_coeff_(1, 3) = (lr_ * cr_ - lf_ * cf_) / mass_;
matrix_a_coeff_(2, 3) = 1.0;
matrix_a_coeff_(3, 1) = (lr_ * cr_ - lf_ * cf_) / iz_;
matrix_a_coeff_(3, 3) = -1.0 * (lf_ * lf_ * cf_ + lr_ * lr_ * cr_) / iz_;
// 初始化(连续型)车辆横向动力学模型 -- 矩阵B
matrix_b_ = Matrix::Zero(basic_state_size_, controls_);
matrix_b_(1, 0) = cf_ / mass_;
matrix_b_(3, 0) = lf_ * cf_ / iz_;
matrix_b_(4, 1) = 0.0;
matrix_b_(5, 1) = -1.0;
// 初始化(离散型)车辆横向动力学模型 -- 矩阵Ad
matrix_ad_ = Matrix::Zero(basic_state_size_, basic_state_size_);
// 初始化(离散型)车辆横向动力学模型 -- 矩阵Bd
matrix_bd_ = Matrix::Zero(basic_state_size_, controls_);
matrix_bd_ = matrix_b_ * ts_;
// 初始化(离散型)车辆横向动力学方程 -- 状态量x
matrix_state_ = Matrix::Zero(basic_state_size_, 1);
// 初始化代价函数J -- 矩阵R
matrix_r_ = Matrix::Identity(controls_, controls_);
matrix_r_(0, 0) = 3.25; // 方向盘转角
matrix_r_(1, 1) = 1.0; // 车辆加速度(总价速度)
// 初始化代价函数J -- 矩阵Q
matrix_q_ = Matrix::Zero(basic_state_size_, basic_state_size_);
matrix_q_(0, 0) = 3.0; // 横向误差
matrix_q_(1, 1) = 0.0; // 横向误差变化率
matrix_q_(2, 2) = 15.0; // 朝向误差
matrix_q_(3, 3) = 0.0; // 朝向误差变化率
matrix_q_(4, 4) = 0.0; // 纵向位置误差
matrix_q_(5, 5) = 10; // 纵向速度误差
return;
}
// 函数作用:计算目标点和车辆当前位置之间距离的平方
double PointDistanceSquare(const TrajectoryPoint &point, const double x, const double y) {
const double dx = point.x - x;
const double dy = point.y - y;
return dx * dx + dy * dy;
}
// 函数作用:将弧度值归化到 [-M_PI, M_PI] 之间,防止弧度值超过量纲
double NormalizeAngle(const double angle) {
double a = std::fmod(angle + M_PI, 2.0 * M_PI);
if (a < 0.0) a += (2.0 * M_PI);
return a - M_PI;
}
// 函数作用:
double MPCController::Wheel2SteerPct(const double wheel_angle) {
return wheel_angle / wheel_single_direction_max_degree_ * 100;
}
// 函数作用:计算控制命令
bool MPCController::ComputeControlCommand(const VehicleState &localization, const TrajectoryData &planning_published_trajectory, ControlCmd &cmd) {
// 所有轨迹点(全局规划器提供的全局路径)
trajectory_points_ = planning_published_trajectory.trajectory_points;
// 更新当前时间步的状态空间变量 x_0(均为误差量)
UpdateState(localization);
// 更新状态矩阵 Ad
// 解释:因为矩阵Ad的计算涉及到车速vx,所以每往后走一个时间步,都要同步更新一下系统横向动力学模型中的Ad矩阵
UpdateMatrix(localization);
// 初始化控制量u的矩阵
Matrix control_matrix = Matrix::Zero(controls_, 1);
// 车辆当前的目标状态量 x_ref(也都是误差量,恒定为 0 向量)
Matrix reference_state = Matrix::Zero(basic_state_size_, 1);
// 初始化控制量u中每个分量的上下限值
// 方向盘转角,车辆加速度
Matrix lower_bound(controls_, 1);
Matrix upper_bound(controls_, 1);
lower_bound << -M_PI/6, max_deceleration_;
upper_bound << M_PI/6, max_acceleration_;
// 初始化状态量x中每个分量的上下限值
// 横向误差,横向误差变化率,航向误差,航向误差变化率,纵向位置误差,纵向速度误差
Matrix lower_state_bound(basic_state_size_, 1);
Matrix upper_state_bound(basic_state_size_, 1);
const double max = std::numeric_limits<double>::max();
lower_state_bound << -1.0 * max, -1.0 * max, -1.0 * M_PI, -1.0 * max, -1.0 * max, -1.0 * max;
upper_state_bound << max, max, M_PI, max, max, max;
// 初始化需要发送给carla模拟器的控制命令
// 方向盘转角,车辆加速度
std::vector<double> control_cmd(controls_, 0);
// 初始化QP求解器
MpcOsqp mpc_osqp(matrix_ad_, // Ad
matrix_bd_, // Bd
matrix_q_, // Q
matrix_r_, // R
matrix_state_, // x0
lower_bound, // 不等式约束
upper_bound, // 不等式约束
lower_state_bound, // 不等式约束
upper_state_bound, // 不等式约束
reference_state, // 车辆当前位置匹配的目标点的 -- 目标状态量 xref
mpc_max_iteration_, // QP求解器最大迭代次数
horizon_, // 有限时域长度
mpc_eps_); // 计算阈值
// 调用QP求解器开始计算具体的控制命令
if (!mpc_osqp.Solve(&control_cmd)) {
std::cout << "MPC OSQP solver failed" << std::endl;
}
else {
std::cout << "MPC OSQP problem solved" << std::endl;
control_matrix(0, 0) = control_cmd.at(0);
control_matrix(1, 0) = control_cmd.at(1);
}
// 发布控制命令
double steer_angle_feedback = control_matrix(0, 0);
double acc_feedback = control_matrix(1, 0);
cmd.steer_target = steer_angle_feedback;
cmd.acc = acc_feedback;
return true;
}
// 函数作用:更新状态空间变量x
void MPCController::UpdateState(const VehicleState &vehicle_state) {
// 智能指针
std::shared_ptr<LateralControlError> lat_con_err = std::make_shared<LateralControlError>();
// 计算状态量x中的每个分量(存储在变量 lat_con_err 中)
ComputeErrors(vehicle_state.x, vehicle_state.y, vehicle_state.heading, vehicle_state.velocity, vehicle_state.angular_velocity, vehicle_state.acceleration, lat_con_err);
// 更新状态量x中的每个分量
matrix_state_(0, 0) = lat_con_err->lateral_error; // 横向误差
matrix_state_(1, 0) = lat_con_err->lateral_error_rate; // 横向误差变化率
matrix_state_(2, 0) = lat_con_err->heading_error; // 朝向误差
matrix_state_(3, 0) = lat_con_err->heading_error_rate; // 朝向误差变化率
matrix_state_(4, 0) = station_error_; // 纵向位置误差
matrix_state_(5, 0) = speed_error_; // 纵向速度误差
}
// 函数作用:更新矩阵 A_d (计算车辆横向动力学模型 -- 矩阵A + 矩阵Ad)
void MPCController::UpdateMatrix(const VehicleState &vehicle_state) {
// 防止车辆速度为0
double v;
v = std::max(vehicle_state.velocity, minimum_speed_protection_);
// 计算(连续型)车辆横向动力学模型 -- 矩阵A
matrix_a_(1, 1) = matrix_a_coeff_(1, 1) / v;
matrix_a_(1, 3) = matrix_a_coeff_(1, 3) / v;
matrix_a_(3, 1) = matrix_a_coeff_(3, 1) / v;
matrix_a_(3, 3) = matrix_a_coeff_(3, 3) / v;
// 计算(离散型)车辆横向动力学模型 -- 矩阵Ad
Matrix matrix_i = Matrix::Identity(matrix_a_.cols(), matrix_a_.cols());
matrix_ad_ = (matrix_i - ts_ * 0.5 * matrix_a_).inverse() * (matrix_i + ts_ * 0.5 * matrix_a_);
}
// 函数作用:计算状态空间变量x的每个分量
void MPCController::ComputeErrors(const double x, const double y, const double theta, const double linear_v, const double angular_v, const double linear_a, LateralControlErrorPtr& lat_con_err) {
// 查询距离车辆当前位置最近的路径点作为目标点
TrajectoryPoint target_point;
target_point = QueryNearestPointByPosition(x, y);
const double dx = x - target_point.x;
const double dy = y - target_point.y;
const double cos_target_heading = std::cos(target_point.heading);
const double sin_target_heading = std::sin(target_point.heading);
double lateral_error = cos_target_heading * dy - sin_target_heading * dx; // 横向误差(使用的是车身坐标系和全局坐标系的变换公式计算的)
double heading_error = NormalizeAngle(theta - target_point.heading); // 航向误差
auto lateral_error_dot = linear_v * std::sin(heading_error); // 横向误差变化率
double ref_heading_rate = target_point.kappa * target_point.v; // 航向误差变化率
station_error_ = -(dx * cos_target_heading + dy * sin_target_heading); // 纵向位置误差
speed_error_ = target_point.v - linear_v * std::cos(abs(heading_error)) / (1 - target_point.kappa * lateral_error); // 纵向速度误差
lat_con_err->lateral_error = lateral_error;
lat_con_err->heading_error = heading_error;
lat_con_err->lateral_error_rate = lateral_error_dot;
lat_con_err->heading_error_rate = angular_v - ref_heading_rate;
}
// 函数作用:返回全局规划路径上,距离车辆当前位置最近的点
TrajectoryPoint MPCController::QueryNearestPointByPosition(const double x, const double y) {
double d_min = PointDistanceSquare(trajectory_points_.front(), x, y);
size_t index_min = 0;
for (size_t i = 1; i < trajectory_points_.size(); ++i) {
double d_temp = PointDistanceSquare(trajectory_points_[i], x, y);
if (d_temp < d_min) {
d_min = d_temp;
index_min = i;
}
}
return trajectory_points_[index_min];
}
} // namespace control
} // namespace shenlan- 头文件 mpc_osqp.h :定义 QP 问题所涉及的所有矩阵和信息
#pragma once
#include <algorithm>
#include <limits>
#include <memory>
#include <utility>
#include <vector>
#include "Eigen/Eigen"
#include "osqp/osqp.h"
namespace shenlan {
namespace control {
class MpcOsqp {
public:
/**
* @brief Solver for discrete-time model predictive control problem.
* @param matrix_a The system dynamic matrix
* @param matrix_b The control matrix
* @param matrix_q The cost matrix for control state costfunction
* @param matrix_lower The lower bound control constrain matrix
* @param matrix_upper The upper bound control constrain matrix
* @param matrix_initial_state The initial state matrix
* @param max_iter The maximum iterations
*/
MpcOsqp(const Eigen::MatrixXd &matrix_a, const Eigen::MatrixXd &matrix_b, // Ad, Bd
const Eigen::MatrixXd &matrix_q, const Eigen::MatrixXd &matrix_r, // Q , R
const Eigen::MatrixXd &matrix_initial_x, // 初始状态空间
const Eigen::MatrixXd &matrix_u_lower, // 控制变量下界
const Eigen::MatrixXd &matrix_u_upper, // 控制变量上界
const Eigen::MatrixXd &matrix_x_lower, // 状态变量下界
const Eigen::MatrixXd &matrix_x_upper, // 状态变量上界
const Eigen::MatrixXd &matrix_x_ref, // 车辆当前位置匹配的目标点的 -- 目标状态量x
const int max_iter, // QP 求解器的最大迭代次数
const int horizon, // MPC 的有限时域长度
const double eps_abs); // QP 求解器的计算阈值
bool Solve(std::vector<double> *control_cmd);
private:
void CalculateKernel(std::vector<c_float> *P_data, std::vector<c_int> *P_indices, std::vector<c_int> *P_indptr); // 求 P
void CalculateEqualityConstraint(std::vector<c_float> *A_data, std::vector<c_int> *A_indices, std::vector<c_int> *A_indptr); // 求 A_c
void CalculateGradient(); // 求 q
void CalculateConstraintVectors(); // 求 l 和 u
OSQPSettings* Settings();
OSQPData* Data();
void FreeData(OSQPData *data);
template <typename T>
T *CopyData(const std::vector<T> &vec) {
T* data = new T[vec.size()];
memcpy(data, vec.data(), sizeof(T) * vec.size());
return data;
}
private:
Eigen::MatrixXd matrix_a_; // Ad
Eigen::MatrixXd matrix_b_; // Bd
Eigen::MatrixXd matrix_q_; // Q
Eigen::MatrixXd matrix_r_; // R
Eigen::MatrixXd matrix_initial_x_; // x_0
const Eigen::MatrixXd matrix_u_lower_; //
const Eigen::MatrixXd matrix_u_upper_; //
const Eigen::MatrixXd matrix_x_lower_; //
const Eigen::MatrixXd matrix_x_upper_; //
const Eigen::MatrixXd matrix_x_ref_; // x_ref
size_t state_dim_;
size_t control_dim_;
size_t num_param_;
int num_constraint_;
int max_iteration_;
size_t horizon_;
double eps_abs_;
Eigen::VectorXd gradient_; // q 矩阵
Eigen::VectorXd lowerBound_; // l 向量
Eigen::VectorXd upperBound_; // u 向量
// 注:没有定义矩阵 P 和 A_c ,因为这俩都是稀疏矩阵,而且很大,如果直接存储太消耗资源,所以使用列压缩的方式转化为了3个特征数组
};
} // namespace control
} // namespace shenlan- 源文件 mpc_osqp.cpp :
#include "mpc_osqp.h"
namespace shenlan {
namespace control {
// 函数作用:有参构造函数
MpcOsqp::MpcOsqp(const Eigen::MatrixXd &matrix_a, // Ad
const Eigen::MatrixXd &matrix_b, // Bd
const Eigen::MatrixXd &matrix_q, // Q
const Eigen::MatrixXd &matrix_r, // R
const Eigen::MatrixXd &matrix_initial_x, // x_0(当前时间步系统初始状态量)
const Eigen::MatrixXd &matrix_u_lower, // 控制量u的下界(维数:2 -- 横向1个 + 纵向1个)
const Eigen::MatrixXd &matrix_u_upper, // 控制量u的上界
const Eigen::MatrixXd &matrix_x_lower, // 状态量x的下界(维数:6 -- 横向4个 + 纵向2个)
const Eigen::MatrixXd &matrix_x_upper, // 状态量x的上界
const Eigen::MatrixXd &matrix_x_ref, // x_ref(当前时间步目标状态量,恒定为 0)
const int max_iter, // QP 求解器的最大迭代次数
const int horizon, // MPC 的有限时域长度
const double eps_abs) // QP 求解器的计算阈值
:
matrix_a_(matrix_a), // 6 * 6 非定值
matrix_b_(matrix_b), // 6 * 2 定值
matrix_q_(matrix_q), // 6 * 6 定值
matrix_r_(matrix_r), // 2 * 2 定值
matrix_initial_x_(matrix_initial_x), // 6 * 1 非定值
matrix_u_lower_(matrix_u_lower), // 2 * 1 定值
matrix_u_upper_(matrix_u_upper), // 2 * 1 定值
matrix_x_lower_(matrix_x_lower), // 6 * 1 定值
matrix_x_upper_(matrix_x_upper), // 6 * 1 定值
matrix_x_ref_(matrix_x_ref), // 6 * 1 定值(恒定为0)
max_iteration_(max_iter),
horizon_(horizon),
eps_abs_(eps_abs) {
state_dim_ = matrix_b.rows(); // 状态量数目:6
control_dim_ = matrix_b.cols(); // 控制量数目:2
num_param_ = state_dim_ * (horizon_ + 1) + control_dim_ * horizon_; // 代价函数涉及参数数目:6 * (10 + 1) + 2 * 10
}
// 函数作用:计算 P 矩阵,并将稀疏矩阵 P 表示为 csc_matrix(压缩列存储)格式
void MpcOsqp::CalculateKernel(std::vector<c_float> *P_data, std::vector<c_int> *P_indices, std::vector<c_int> *P_indptr) {
// P_data 稀疏矩阵 P 内的所有非零数值
// P_indices 稀疏矩阵 P 内每一列上的非零数字的行索引值
// P_indptr 稀疏矩阵 P 内截止到到当前列(不含当前列)所有非零数字的数量
// 注意:这三个数组是将稀疏矩阵 P 的内容提炼了出来,将这三个数组传入,就知道他们原本代表的稀疏矩阵 P 的样子了
// 注意:这三个数组均为函数 csc_matrix() 的参数,函数的作用是通过传入的三个数组,恢复稀疏矩阵 P 原有的样子
// 初始化数组 columns
// 这个数组没什么特别的含义,只是一个中间量,是为了后面求解数组 P_data / P_indices / P_indptr 更方便
// 这个数组用来按列存放稀疏矩阵 P 中每个非零元素,从左到右按顺序遍历稀疏矩阵 P 的每一列,一次寻找一列内的所有非零元素,存放内容为 pair(非零元素所在行索引 , 非零元素值)
std::vector<std::vector<std::pair<c_int, c_float>>> columns;
// 外侧数组 -- 外壳
// 内侧数组 -- 代表按列
columns.resize(num_param_);
// 临时变量
// 作用:用来计数到目前为止遍历到的稀疏矩阵 P 中非零元素的个数
int value_index = 0;
// 数组 columns 中 -- 稀疏矩阵 P 的左上角对角阵 diag(Q , Q , ... , Q) 对应的部分(N + 1个Q)(N = horizon_)
for (size_t i = 0; i <= horizon_; ++i) { // 按 Q 块
for (size_t j = 0; j < state_dim_; ++j) { // 按列
// 使用函数 emplace_back() 在数组 columns 的尾部添加新元素 -- pair(行索引 , 非零数值)
columns[i * state_dim_ + j].emplace_back(i * state_dim_ + j, matrix_q_(j, j));
++value_index;
}
}
// 数组 columns 中 -- 稀疏矩阵 P 的右下角对角阵 diag(R , R , ... , R) 对应的部分(N个R)
const size_t state_total_dim = state_dim_ * (horizon_ + 1);
for (size_t i = 0; i < horizon_; ++i) { // 按 R 块
for (size_t j = 0; j < control_dim_; ++j) { // 按列
columns[i * control_dim_ + j + state_total_dim].emplace_back(i * control_dim_ + j + state_total_dim, matrix_r_(j, j));
++value_index;
}
}
// 到此为止得到完整的数组 columns ;
// 临时变量
// 作用:用来计数遍历到当前列(不包含该列)时,累计的非零元素的数量
int ind_p = 0;
// 使用数组 columns 得到数组 P_data / P_indices / P_indptr
// 对于 P 矩阵,相当于按列遍历
for (size_t i = 0; i < num_param_; ++i) { // 按列
P_indptr->emplace_back(ind_p);
for (const auto &row_data_pair : columns[i]) { // columns[i] 里的内容为第 i 列中所有非零元素的 pair 对
P_data->emplace_back(row_data_pair.second);
P_indices->emplace_back(row_data_pair.first);
++ind_p;
}
}
P_indptr->emplace_back(ind_p);
}
// 函数作用:计算 q 矩阵
// 注意:车辆在每个时间步的目标状态量 x_ref 都是 0 向量,因为状态量本社就是误差量,我们的目的就是让误差量全为 0
void MpcOsqp::CalculateGradient() {
gradient_ = Eigen::VectorXd::Zero(state_dim_ * (horizon_ + 1) + control_dim_ * horizon_, 1);
for (size_t i = 0; i < horizon_ + 1; i++) {
gradient_.block(i * state_dim_, 0, state_dim_, 1) = -1.0 * matrix_q_ * matrix_x_ref_;
}
}
// 函数作用:计算 A_c 矩阵,并将稀疏矩阵 A_c 表示为 csc_matrix(压缩列存储)格式
void MpcOsqp::CalculateEqualityConstraint(std::vector<c_float> *A_data, std::vector<c_int> *A_indices, std::vector<c_int> *A_indptr) {
static constexpr double kEpsilon = 1e-6;
Eigen::MatrixXd control_identity_mat = Eigen::MatrixXd::Identity(control_dim_, control_dim_);
// 初始化矩阵 A_c
Eigen::MatrixXd matrix_constraint = Eigen::MatrixXd::Zero(state_dim_ * (horizon_ + 1) + state_dim_ * (horizon_ + 1) + control_dim_ * horizon_, state_dim_ * (horizon_ + 1) + control_dim_ * horizon_);
// 填充矩阵 A_c
Eigen::MatrixXd state_identity_mat = Eigen::MatrixXd::Identity(state_dim_ * (horizon_ + 1), state_dim_ * (horizon_ + 1));
matrix_constraint.block(0, 0, state_dim_ * (horizon_ + 1), state_dim_ * (horizon_ + 1)) = -1 * state_identity_mat;
for (size_t i = 0; i < horizon_; i++) {
matrix_constraint.block((i + 1) * state_dim_, i * state_dim_, state_dim_, state_dim_) = matrix_a_;
}
for (size_t i = 0; i < horizon_; i++) {
matrix_constraint.block((i + 1) * state_dim_, i * control_dim_ + (horizon_ + 1) * state_dim_, state_dim_, control_dim_) = matrix_b_;
}
Eigen::MatrixXd all_identity_mat = Eigen::MatrixXd::Identity(num_param_, num_param_);
matrix_constraint.block(state_dim_ * (horizon_ + 1), 0, num_param_, num_param_) = all_identity_mat;
// 将矩阵 A_c 表示为按列压缩格式
std::vector<std::vector<std::pair<c_int, c_float>>> columns;
columns.resize(num_param_ + 1);
int value_index = 0;
// 得到 columns 数组,用来后续辅助生成 3 个特征数组
for (size_t i = 0; i < num_param_; ++i) { // col
for (size_t j = 0; j < num_param_ + state_dim_ * (horizon_ + 1); ++j) { // row
if (std::fabs(matrix_constraint(j, i)) > kEpsilon) {
// (row, val)
columns[i].emplace_back(j, matrix_constraint(j, i));
++value_index;
}
}
}
// 求出按列压缩 A_c 的 3 个特征数组
int ind_A = 0;
for (size_t i = 0; i < num_param_; ++i) {
A_indptr->emplace_back(ind_A);
for (const auto &row_data_pair : columns[i]) {
A_data->emplace_back(row_data_pair.second);
A_indices->emplace_back(row_data_pair.first);
++ind_A;
}
}
A_indptr->emplace_back(ind_A);
}
// 函数作用:计算约束向量 l 和 u
void MpcOsqp::CalculateConstraintVectors() {
// 不等式约束形成的上下界:[xmin , xmin , ... , xmin | umin , umin , ... umin ]
Eigen::VectorXd lowerInequality = Eigen::MatrixXd::Zero(state_dim_ * (horizon_ + 1) + control_dim_ * horizon_, 1);
Eigen::VectorXd upperInequality = Eigen::MatrixXd::Zero(state_dim_ * (horizon_ + 1) + control_dim_ * horizon_, 1);
// 控制量 u 的上下界
for (size_t i = 0; i < horizon_; i++) {
lowerInequality.block(control_dim_ * i + state_dim_ * (horizon_ + 1), 0, control_dim_, 1) = matrix_u_lower_;
upperInequality.block(control_dim_ * i + state_dim_ * (horizon_ + 1), 0, control_dim_, 1) = matrix_u_upper_;
}
// 状态量 x 的上下界
for (size_t i = 0; i < horizon_ + 1; i++) {
lowerInequality.block(state_dim_ * i, 0, state_dim_, 1) = matrix_x_lower_;
upperInequality.block(state_dim_ * i, 0, state_dim_, 1) = matrix_x_upper_;
}
// 等式约束形成的上下界:[ -x0 , 0 , 0 , ... , 0 ]
Eigen::VectorXd lowerEquality = Eigen::MatrixXd::Zero(state_dim_ * (horizon_ + 1), 1);
Eigen::VectorXd upperEquality;
lowerEquality.block(0, 0, state_dim_, 1) = -1 * matrix_initial_x_;
upperEquality = lowerEquality;
lowerEquality = lowerEquality;
// 合并等式约束和不等式约束
lowerBound_ = Eigen::MatrixXd::Zero(2 * state_dim_ * (horizon_ + 1) + control_dim_ * horizon_, 1);
lowerBound_ << lowerEquality, lowerInequality;
upperBound_ = Eigen::MatrixXd::Zero(2 * state_dim_ * (horizon_ + 1) + control_dim_ * horizon_, 1);
upperBound_ << upperEquality, upperInequality;
}
// 函数作用:配置 QP 问题的参数
// 注1:返回值是一个 OSQPSettings 结构体的指针
// 注2:OSQPSettings 是 OSQP 库中的一个结构体,用于配置 OSQP 求解器的参数,该结构体中的所有属性都是 QP 问题的参数
// 注3:osqp_set_default_settings 是 OSQP 中的一个函数,作用为将指针指向的 OSQPSettings 结构体初始化为默认的设置值,用户可以根据具体需求进行调整
OSQPSettings* MpcOsqp::Settings() {
// 分配内存:
// 解释:c_malloc 函数作用是分配内存并返回一个 void* 类型的指针,并使用 reinterpret_cast 函数将指针类型强制转化为 OSQPSettings* 类型
OSQPSettings* settings = reinterpret_cast<OSQPSettings *>(c_malloc(sizeof(OSQPSettings)));
// 指针为空代表分配内存失败
if (settings == nullptr) {
return nullptr;
}
else {
osqp_set_default_settings(settings);
settings->polish = true;
settings->scaled_termination = true;
settings->verbose = false;
settings->max_iter = max_iteration_; // QP 最大迭代次数
settings->eps_abs = eps_abs_; // QP 计算精度
return settings;
}
}
// 函数作用:配置 QP 问题的矩阵和向量
// 注1:返回值是一个 OSQPData 结构体的指针
// 注2:OSQPData 是 OSQP 库中的一个结构体,用于存储二次规划(QP)问题的输入数据,OSQPData 包含了定义 QP 问题所需的所有矩阵和向量
OSQPData* MpcOsqp::Data() {
// 分配内存:
OSQPData* data = reinterpret_cast<OSQPData *>(c_malloc(sizeof(OSQPData)));
size_t kernel_dim = state_dim_ * (horizon_ + 1) + control_dim_ * horizon_; // QP 问题需要求解的变量的数量【( x_0 ~ x_N ) + ( u_0 ~ u_N-1 )】
size_t num_affine_constraint = 2 * state_dim_ * (horizon_ + 1) + control_dim_ * horizon_; // QP 问题约束的数量
if (data == nullptr) {
return nullptr;
}
else {
data->n = kernel_dim; // 需要求解的变量的数量
data->m = num_affine_constraint; // 约束的数量 = 等式约束的数量 + 不等式约束的数量
// 初始化稀疏矩阵 P 的 3 个特征数组
std::vector<c_float> P_data;
std::vector<c_int> P_indices;
std::vector<c_int> P_indptr;
// 计算稀疏矩阵 P 的 3 个特征数组
CalculateKernel(&P_data, &P_indices, &P_indptr);
// 通过 3 个特征数组计算出 P 阵,并将 P 阵传入
data->P = csc_matrix(kernel_dim, kernel_dim, P_data.size(), CopyData(P_data), CopyData(P_indices), CopyData(P_indptr));
// 将数组 q 传入
data->q = gradient_.data();
// 初始化稀疏矩阵 A_c 的 3 个特征数组
std::vector<c_float> A_data;
std::vector<c_int> A_indices;
std::vector<c_int> A_indptr;
// 计算稀疏矩阵 A_c 的 3 个特征数组
CalculateEqualityConstraint(&A_data, &A_indices, &A_indptr);
// 通过 3 个特征数组计算出 A_c 阵,并将 A_c 阵传入
data->A = csc_matrix(state_dim_ * (horizon_ + 1) + state_dim_ * (horizon_ + 1) + control_dim_ * horizon_, kernel_dim, A_data.size(), CopyData(A_data), CopyData(A_indices), CopyData(A_indptr));
// 将上下界约束 l 和 u 传入
data->l = lowerBound_.data();
data->u = upperBound_.data();
return data;
}
}
// 函数作用:释放 data 指针指向位置的内存
// 注:使用 c_malloc 函数分配内存,使用 c_free 函数释放内存,这两个函数是配套使用的
void MpcOsqp::FreeData(OSQPData* data) {
c_free(data->A);
c_free(data->P);
c_free(data);
}
// 函数作用:求解 QP 问题
// 返回值:当前时刻的控制命令
bool MpcOsqp::Solve(std::vector<double>* control_cmd) {
CalculateGradient();
CalculateConstraintVectors();
OSQPData* data = Data();
OSQPSettings* settings = Settings();
// 注:OSQPWorkspace 是 OSQP 库中的一个类,用于管理和操作 OSQP 求解器的工作空间,包括定义问题、设置参数、执行求解等功能;这里创建了一个名为 osqp_workspace 的指针指向了这个工作空间
OSQPWorkspace* osqp_workspace = nullptr;
// 注:osqp_setup 函数是用来初始化 OSQP 求解器的工作空间的函数;这个函数的作用是根据传入的数据(data)和设置(settings)来设置和配置 OSQP 求解器的工作环境,以便后续能够使用 OSQP 求解器来解决具体的凸二次规划问题
osqp_workspace = osqp_setup(data, settings);
// 注:osqp_solve 函数的作用是调用 OSQP 求解器来解决已经设置好的凸二次规划问题;osqp_solve(osqp_workspace) 表示你正在使用 osqp_workspace 所指向的 OSQP 求解器工作空间来执行求解操作
osqp_solve(osqp_workspace);
// 完成求解后,求解过程中涉及的所有信息都会存储在 workspace 的 info 中,获得的结果都会存储在在 workspace 的 solution 中;
// 这里取出了求解器的状态信息:
// 1. 求解器状态小于 0:表示求解过程中出现了错误或者未能达到收敛状态
// 2. 求解器状态为 1:表示求解器已经收敛并找到了最优解
// 3. 求解器状态为 2:表示求解器达到了最大迭代次数而停止
auto status = osqp_workspace->info->status_val;
if (status < 0 || (status != 1 && status != 2)) {
osqp_cleanup(osqp_workspace);
FreeData(data);
c_free(settings);
return false;
}
else if (osqp_workspace->solution == nullptr) {
// 注:如果 solution 为 nullptr,表示求解器没有成功生成解
osqp_cleanup(osqp_workspace);
FreeData(data);
c_free(settings);
return false;
}
size_t first_control = state_dim_ * (horizon_ + 1); // 第一个控制量所在位置的索引值
// 因为 QP 问题的变量是 [ x_0 , x_1 , ... , x_N-1 ,x_N | u_0 , u_1 , ... , u_N-1 ]
// 而我们需要的只是当前时刻的控制量 u_0 ,而 u_0 在变量中的位置的索引是 6*(N+1)
// 给控制命令赋值为 u_0
for (size_t i = 0; i < control_dim_; ++i) {
control_cmd->at(i) = osqp_workspace->solution->x[i + first_control];
}
// 清理内存
osqp_cleanup(osqp_workspace);
FreeData(data);
c_free(settings);
return true;
}
} // namespace control
} // namespace shenlan- 头文件 reference_line.h :补全参考线信息
#include <vector>
#include <iostream>
#include <math.h>
namespace shenlan {
namespace control {
class ReferenceLine {
public:
ReferenceLine(const std::vector<std::pair<double, double>>& xy_points);
~ReferenceLine() = default;
// 函数作用:计算参考线。参考线的每个点需要包含以下信息
// 1) xy_pionts_ 路径点坐标
// 2) headings 路径点朝向角
// 3) accumulated_s 路径点累计路程
// 4) kappas 路径点曲率
// 5) dkappas 路径点曲率的变化率
bool ComputePathProfile(std::vector<double>* headings, std::vector<double>* accumulated_s, std::vector<double>* kappas, std::vector<double>* dkappas);
private:
std::vector<std::pair<double, double>> xy_points_; // 用vector装载规划的全局路径上所有点的坐标
};
} // namespace control
} // namespace shenlan- 源文件 reference_line.cpp :
#include "reference_line.h"
namespace shenlan {
namespace control {
// 函数作用:拷贝构造函数
ReferenceLine::ReferenceLine(const std::vector<std::pair<double, double>>& xy_points) { xy_points_ = xy_points; }
// 函数作用:由于全局路径规划期仅仅给出了全局路径信息(即所有点的xy坐标),而没有任何关于这条全局路径的其他几何信息(如每个路径点的 朝向角/距离/曲率/曲率变化率);
// 而我们在局部规划中使用的参考线其实是和全局路径重合的,也就是说参考线上的所有路径点就是全局路径的所有路径点;
// 但是要注意,我们需要的参考线不能仅仅只有每个路径点的坐标,还需要有每个路径点的各个几何信息(如 朝向角/距离/曲率/曲率变化率);
// 因此我们直接计算全局路径中每个路径点的几何信息,然后汇总到一起,就是我们需要的参考线信息;
bool ReferenceLine::ComputePathProfile(std::vector<double>* headings, std::vector<double>* accumulated_s, std::vector<double>* kappas, std::vector<double>* dkappas) {
headings->clear(); // 装载每个路径点的 -- 朝向角
accumulated_s->clear(); // 装载每个路径点的 -- 到达该点时所累积的路径长度(起点到该点的几何路径长度)
kappas->clear(); // 装载每个路径点的 -- 曲率
dkappas->clear(); // 装载每个路径点的 -- 曲率变化率
if (xy_points_.size() < 2) return false;
std::vector<double> dxs; // 路径点处的 -- dx
std::vector<double> dys; // 路径点处的 -- dy
std::vector<double> y_over_s_first_derivatives; // 路径点处的 -- 一阶偏x导数
std::vector<double> x_over_s_first_derivatives; // 路径点处的 -- 一阶偏y导数
std::vector<double> y_over_s_second_derivatives; // 路径点处的 -- 二阶偏x导数
std::vector<double> x_over_s_second_derivatives; // 路径点处的 -- 二阶偏y导数
// 计算每个路径点的x,y差值(即dx,dy)
std::size_t points_size = xy_points_.size();
for (std::size_t i = 0; i < points_size; ++i) {
double x_delta = 0.0;
double y_delta = 0.0;
if (i == 0) {
x_delta = (xy_points_[i + 1].first - xy_points_[i].first);
y_delta = (xy_points_[i + 1].second - xy_points_[i].second);
} else if (i == points_size - 1) {
x_delta = (xy_points_[i].first - xy_points_[i - 1].first);
y_delta = (xy_points_[i].second - xy_points_[i - 1].second);
} else {
x_delta = 0.5 * (xy_points_[i + 1].first - xy_points_[i - 1].first);
y_delta = 0.5 * (xy_points_[i + 1].second - xy_points_[i - 1].second);
}
dxs.push_back(x_delta);
dys.push_back(y_delta);
}
// 计算每个路径点的朝向角
for (std::size_t i = 0; i < points_size; ++i) {
headings->push_back(std::atan2(dys[i], dxs[i]));
}
// 计算每个路径点处的累计路径长度
double distance = 0.0;
accumulated_s->push_back(distance); // 第一个路径点(起点)的 index = 0 ,且在该点处的累计路径长度为 0
double fx = xy_points_[0].first; // 起点横坐标
double fy = xy_points_[0].second; // 起点纵坐标
double nx = 0.0;
double ny = 0.0;
for (std::size_t i = 1; i < points_size; ++i) {
nx = xy_points_[i].first;
ny = xy_points_[i].second;
double end_segment_s = std::sqrt((fx - nx) * (fx - nx) + (fy - ny) * (fy - ny));
accumulated_s->push_back(end_segment_s + distance);
distance += end_segment_s;
fx = nx;
fy = ny;
}
// 计算每个路径点相对于路径长度ds的x和y的一阶导数
for (std::size_t i = 0; i < points_size; ++i) {
double xds = 0.0;
double yds = 0.0;
if (i == 0) {
xds = (xy_points_[i + 1].first - xy_points_[i].first) / (accumulated_s->at(i + 1) - accumulated_s->at(i));
yds = (xy_points_[i + 1].second - xy_points_[i].second) / (accumulated_s->at(i + 1) - accumulated_s->at(i));
} else if (i == points_size - 1) {
xds = (xy_points_[i].first - xy_points_[i - 1].first) / (accumulated_s->at(i) - accumulated_s->at(i - 1));
yds = (xy_points_[i].second - xy_points_[i - 1].second) / (accumulated_s->at(i) - accumulated_s->at(i - 1));
} else {
xds = (xy_points_[i + 1].first - xy_points_[i - 1].first) / (accumulated_s->at(i + 1) - accumulated_s->at(i - 1));
yds = (xy_points_[i + 1].second - xy_points_[i - 1].second) / (accumulated_s->at(i + 1) - accumulated_s->at(i - 1));
}
x_over_s_first_derivatives.push_back(xds);
y_over_s_first_derivatives.push_back(yds);
}
// 计算每个路径点相对于路径长度ds的x和y的二阶导数
for (std::size_t i = 0; i < points_size; ++i) {
double xdds = 0.0;
double ydds = 0.0;
if (i == 0) {
xdds = (x_over_s_first_derivatives[i + 1] - x_over_s_first_derivatives[i]) / (accumulated_s->at(i + 1) - accumulated_s->at(i));
ydds = (y_over_s_first_derivatives[i + 1] - y_over_s_first_derivatives[i]) / (accumulated_s->at(i + 1) - accumulated_s->at(i));
} else if (i == points_size - 1) {
xdds = (x_over_s_first_derivatives[i] - x_over_s_first_derivatives[i - 1]) / (accumulated_s->at(i) - accumulated_s->at(i - 1));
ydds = (y_over_s_first_derivatives[i] - y_over_s_first_derivatives[i - 1]) / (accumulated_s->at(i) - accumulated_s->at(i - 1));
} else {
xdds = (x_over_s_first_derivatives[i + 1] - x_over_s_first_derivatives[i - 1]) / (accumulated_s->at(i + 1) - accumulated_s->at(i - 1));
ydds = (y_over_s_first_derivatives[i + 1] - y_over_s_first_derivatives[i - 1]) / (accumulated_s->at(i + 1) - accumulated_s->at(i - 1));
}
x_over_s_second_derivatives.push_back(xdds);
y_over_s_second_derivatives.push_back(ydds);
}
// 计算每个路径点处的曲率
for (std::size_t i = 0; i < points_size; ++i) {
double xds = x_over_s_first_derivatives[i];
double yds = y_over_s_first_derivatives[i];
double xdds = x_over_s_second_derivatives[i];
double ydds = y_over_s_second_derivatives[i];
double kappa = (xds * ydds - yds * xdds) / (std::sqrt(xds * xds + yds * yds) * (xds * xds + yds * yds) + 1e-6);
// 注1:曲率计算公式的分母上加上一个很小的数,防止除法失效
// 注2:这里对曲率的计算使用的是精确公式,而代码中我们在进行动力学建模,计算连续误差型状态空间方程的状态量x时(如:航向误差变化率),则是将曲率视为了半径的倒数,这是一种对曲率的估算方式;
kappas->push_back(kappa);
}
// 计算每个路径点处的曲率变化率
for (std::size_t i = 0; i < points_size; ++i) {
double dkappa = 0.0;
if (i == 0) {
dkappa = (kappas->at(i + 1) - kappas->at(i)) / (accumulated_s->at(i + 1) - accumulated_s->at(i));
} else if (i == points_size - 1) {
dkappa = (kappas->at(i) - kappas->at(i - 1)) / (accumulated_s->at(i) - accumulated_s->at(i - 1));
} else {
dkappa = (kappas->at(i + 1) - kappas->at(i - 1)) / (accumulated_s->at(i + 1) - accumulated_s->at(i - 1));
}
dkappas->push_back(dkappa);
}
return true;
}
} // namespace control
} // namespace shenlan- 主函数:
#include "mpc_controller.h"
using namespace std;
bool first_record_ = true; // 起点标志
VehicleState vehicle_state_; // 车辆状态
ControlCmd cmd_pub; // 控制命令
ros::Publisher acc_pub; // 声明了一个 ROS 发布者对象【将信息发布到一个或多个主题(Topic)上,使得其他 ROS 节点可以订阅(Subscribe)并接收这些消息】
// 函数作用:通过读取 IMU 传感器的数据,得到车辆当前的姿态信息
void IMUCallback(const sensor_msgs::Imu::ConstPtr& msg) {
// 角速度(绕z轴转动的角速度)
vehicle_state_.angular_velocity = msg->angular_velocity.z;
// 加速度(线性加速度)
vehicle_state_.acceleration = sqrt(msg->linear_acceleration.x * msg->linear_acceleration.x + msg->linear_acceleration.y * msg->linear_acceleration.y);
}
// 函数作用:通过读取 ODOM 传感器的数据,得到车辆当前的位置信息
void odomCallback(const nav_msgs::Odometry::ConstPtr& msg) {
if(first_record_) {
vehicle_state_.planning_init_x = msg->pose.pose.position.x;
vehicle_state_.planning_init_y = msg->pose.pose.position.y;
first_record_ = false;
}
vehicle_state_.x = msg->pose.pose.position.x;
vehicle_state_.y = msg->pose.pose.position.y;
vehicle_state_.last_velocity = vehicle_state_.velocity;
vehicle_state_.last_v_time = vehicle_state_.cur_v_time;
vehicle_state_.last_v_err = vehicle_state_.last_velocity - 5;
// 将 ROS 消息中的姿态信息(四元数表示的 orientation)转换为欧拉角(roll, pitch, yaw)形式,并存储到 vehicle_state_ 结构体的对应成员变量中
// 1. 声明了一个名为 q 的 tf::Quaternion 类型的变量,用于存储姿态信息的四元数表示;
tf::Quaternion q;
// 2. 将 ROS 消息中的姿态信息(msg->pose.pose.orientation)转换为 tf::Quaternion 类型并放在 q 变量内;
// quaternionMsgToTF() 是一个 ROS 中的函数,用于将 ROS 消息中的四元数表示转换为 TF 库中的四元数表示;
tf::quaternionMsgToTF(msg->pose.pose.orientation, q);
// 3. 将 q 转换为一个 3x3 的旋转矩阵,然后调用 getRPY 方法,将该旋转矩阵转换为欧拉角(Roll, Pitch, Yaw),并存储到 vehicle_state_ 的对应成员变量中;
tf::Matrix3x3(q).getRPY(vehicle_state_.roll, vehicle_state_.pitch, vehicle_state_.yaw);
vehicle_state_.heading = vehicle_state_.yaw;
vehicle_state_.velocity = std::sqrt(msg->twist.twist.linear.x * msg->twist.twist.linear.x + msg->twist.twist.linear.y * msg->twist.twist.linear.y);
vehicle_state_.cur_v_err = vehicle_state_.velocity - 5;
vehicle_state_.cur_v_time = ros::Time::now().toSec(); // 利用 ROS 提供的时间函数获取当前系统时间,并将其转换为秒数
}
// 主函数
int main(int argc, char** argv) {
// 声明文件流对象,用于打开和读取文件:
std::ifstream infile;
infile.open("src/mpc_control/data/reference_line.txt"); // 将文件流对象与文件连接起来
assert(infile.is_open()); // 若失败,则输出错误消息,并终止程序运行
std::vector<std::pair<double, double>> xy_points; // 存放所有参考点的坐标
std::string x; // 临时变量
std::string y; // 临时变量
std::string s; // 使用该变量逐行读取文件内容
while (getline(infile, s)) {
std::stringstream word(s);
word >> x;
word >> y;
double pt_x = std::atof(x.c_str());
double pt_y = std::atof(y.c_str());
xy_points.push_back(std::make_pair(pt_x, pt_y));
}
// 关闭文件流:
infile.close();
// 补全每个参考点的信息:(当前只有每个参考点的位置坐标)
std::vector<double> headings;
std::vector<double> accumulated_s;
std::vector<double> kappas;
std::vector<double> dkappas;
std::unique_ptr<shenlan::control::ReferenceLine> reference_line = std::make_unique<shenlan::control::ReferenceLine>(xy_points);
reference_line->ComputePathProfile(&headings, &accumulated_s, &kappas, &dkappas);
// 通过参考线信息构建目标轨迹:
TrajectoryData planning_published_trajectory;
for (size_t i = 0; i < headings.size(); i++) {
TrajectoryPoint trajectory_pt;
trajectory_pt.x = xy_points[i].first;
trajectory_pt.y = xy_points[i].second;
trajectory_pt.v = 5.0; // 目标速度
trajectory_pt.a = 0.0; // 目标加速度
trajectory_pt.heading = headings[i];
trajectory_pt.kappa = kappas[i];
planning_published_trajectory.trajectory_points.push_back(trajectory_pt);
}
// 使用 ROS 的 API 进行初始化和设置 ROS 节点的基本步骤
// 1. ros::init 是 ROS 提供的初始化函数,用于初始化 ROS 系统;它需要传入命令行参数 argc 和 argv 以及一个节点名称 control_pub ;
ros::init(argc, argv, "control_pub");
// 2. ros::NodeHandle 是 ROS 中的一个类,用于与 ROS 系统进行通信;这里创建了一个名为 nh 的 NodeHandle 对象,用于管理 ROS 节点的通信和资源;
ros::NodeHandle nh;
// 3. ROS_INFO 是 ROS 提供的一个宏,用于打印消息到ROS的日志系统中,这里表示节点初始化完成;
ROS_INFO("init !");
// 4. subscribe 是 NodeHandle 对象的方法,用于订阅ROS主题;
// 这行代码创建了一个名为 sub 的订阅者对象,订阅了主题 "/odom" ,缓冲区大小为 10 ,回调函数为 odomCallback;当节点收到来自 "/odom" 主题的消息时,将调用 odomCallback 函数进行处理;
ros::Subscriber sub = nh.subscribe("/odom", 10, odomCallback);
// 5. 创建了一个名为 sub_imu 的订阅者对象,订阅了主题 "/imu_raw" ,缓冲区大小为 10 ,回调函数为 IMUCallback;当节点收到来自 "/imu_raw" 主题的消息时,将调用 IMUCallback 函数进行处理;
ros::Subscriber sub_imu = nh.subscribe("/imu_raw", 10, IMUCallback);
// 6. advertise 是 NodeHandle 对象的方法,用于发布ROS主题;
// 这行代码创建了一个名为 control_pub 的发布者对象,发布类型为 lgsvl_msgs::VehicleControlData 的消息到主题 "/vehicle_cmd",并指定了发布队列的大小为1000 ;
// 这意味着节点可以同时缓存 1000 条待发布的消息,超过这个数量后新的消息将被丢弃;
ros::Publisher control_pub = nh.advertise<lgsvl_msgs::VehicleControlData>("/vehicle_cmd", 1000);
// 7. 在 ROS 中创建了一个新的发布者对象 acc_pub ,用于向主题 "/acc_pub_cmd" 发布消息类型为 lgsvl_msgs::VehicleControlData 的数据;
acc_pub = nh.advertise<lgsvl_msgs::VehicleControlData>("/acc_pub_cmd", 1000);
// MPC 控制部分:
ControlCmd cmd;
std::unique_ptr<shenlan::control::MPCController> mpc_controller = std::make_unique<shenlan::control::MPCController>();
mpc_controller->Init();
lgsvl_msgs::VehicleControlData control_cmd;
lgsvl_msgs::VehicleControlData control_cmd_pub;
ros::Rate loop_rate(100);
while (ros::ok()) {
mpc_controller->ComputeControlCommand(vehicle_state_, planning_published_trajectory, cmd);
control_cmd.header.stamp = ros::Time::now();
cout << "vehical_state_.last_v_err: " << vehicle_state_.last_v_err << endl;
cout << "vehical_state_.cur_v_err: " << vehicle_state_.cur_v_err << endl;
cout << "cur_acc: " << (vehicle_state_.cur_v_err - vehicle_state_.last_v_err) / (vehicle_state_.cur_v_time - vehicle_state_.last_v_time) << endl;
cout << "cmd.acc: " << cmd.acc << endl;
control_cmd.acceleration_pct = cmd.acc;
control_cmd.target_gear = lgsvl_msgs::VehicleControlData::GEAR_DRIVE;
control_cmd.target_wheel_angle = -cmd.steer_target;
control_pub.publish(control_cmd);
control_cmd_pub.acceleration_pct = vehicle_state_.acceleration;
acc_pub.publish(control_cmd_pub);
ros::spinOnce();
loop_rate.sleep();
}
return 0;
}