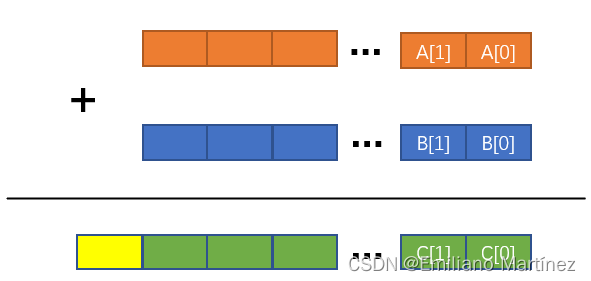
行列式公式
学习了关于行列式的这么多性质，现在我们有能力推导二阶行列式公式了：
观察上面的推导过程，不难发现，行列式的值等于使用性质3.b 分解后所得的那些非零行列式的和，所谓的非零行列式也即该行列式各行各列都有元素，故值不为零。
带着这个重要发现，我们继续尝试计算三阶行列式。以同样的步骤，先保持第2 ，3 行不变，将第1 行
进行拆分得到3 个行列式，分别对这3 个行列式的第2 行进行拆分得到共9 个行列式，再接着拆分这 9
个行列式的第3 行，最终得到27 个行列式，而我们只需要其中的非零行列式：
代数余子式
回顾上面的3 X 3 矩阵，我们已经得到了它的行列式公式：
容3 X 3 的行列式由2 X 2 行列式组成。事实上， n阶行列式同样可化为多个n - 1 阶行列式的组合。下面我们正式介绍代数余子式的概念：
- 改写中的括号部分就是代数余子式。 比如（a22a33 - a23a32）就是a11的代数余子式，（-a21a33 + a23a31）就是a12的代数余子式。
- **代数余子式 (cofactors) 是与选定元素配套的，**这也即 ‘co-’ 的意思。
- 选定元素aij的代数余子式即为：将原行列式中的第i行和第j列抹去后得到的n - 1阶行列式，再取正负(i + j为偶时取+，i+j为奇时取-)，整个记为Cij：
基于代数余子式的概念，我们容易给出新的求行列式的公式：
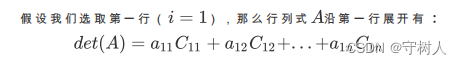
到目前为止，我们学习了三种求解行列式的方法，总结如下： - 消元，将矩阵化为三角矩阵，主元乘积记为行列式的值（最简单）
- 按照行列式公式将行列式完全展开，找到 种非零行列式，计算这些行列式的值的和（最复杂）
- 使用代数余子式对行列式进行降阶，展开得到更简单的行列式，然后再求解（介于二者之间）
下面我们举由 1组成的三对角矩阵为例，来熟悉如何使用代数余子式求解行列式：
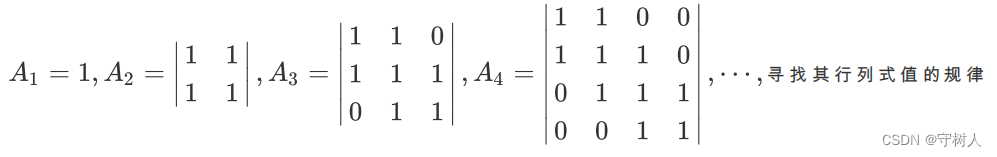
对于A1和A2能够迅速求出其行列式（利用性质）：A1 = 1，A2 = 0。
对于A3无法一眼看出答案，这里可以就A3使用这种新方法：
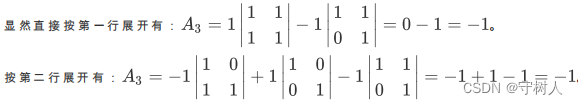
注意到，按第二行展开时，这与不等于0的aij 的个数有关。在使用代数余子式求行列式时，应该尽量选取 0元素多的行。如果各行 0元素都很少，那么根据消元不改变行列式的性质（性质5 ），我们可以先对矩阵进行消元，以得到 0元素多的行，然后再使用代数余子式进行行列式的求解。
需要补充说明的是，使用代数余子式求行列式时可以按行展开，也可以按列展开（性质10 ），比
如上式中的
，可以选取第一列展开（因为第一列 元素多），那么易得
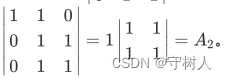
综上，|A4| = |A3| - |A2| = -1 - 0 = -1。猜想由1组成的三对角矩阵的行列式值的规律可能正是|An| = |An-1| - |An-2| ，事实上，这确实就是由1组成的三对角矩阵行列式值的规律，这是由1组成的三对角矩阵的特殊结构所决定的。
由此规律，易得|A5| = 0，|A6| = 1 ，|A7| = 1 ，|A8| = 0，到这里发现：由1组成的n阶三对角矩阵的行列式值从1阶开始按照1,0,-1,-1,0,1循环，周期为6。
