文章目录
- 回归问题和分类问题
- 问题提出
- 逻辑回归
- 二分类问题
- 逻辑函数
- 与线性回归方程的不同
- 模型变化
- loss函数不同
- BCEloss函数的介绍
- 课程代码
课程来源: 链接
课程文本来源借鉴: 链接
以及(强烈推荐) Birandaの
回归问题和分类问题
有监督学习:
- 回归问题
- 分类问题
二分类
多分类
回归问题:如果我们预测的结果是以连续数字进行表示,即我们将在连续函数中对多个输入变量建立映射关系时,则这样的问题称之为回归问题。
分类问题:如果我们预测的结果是以离散形式表示的,即我们将多个输入变量与多个不同的类别建立映射关系时,则这样的问题称之为分类问题。
问题提出
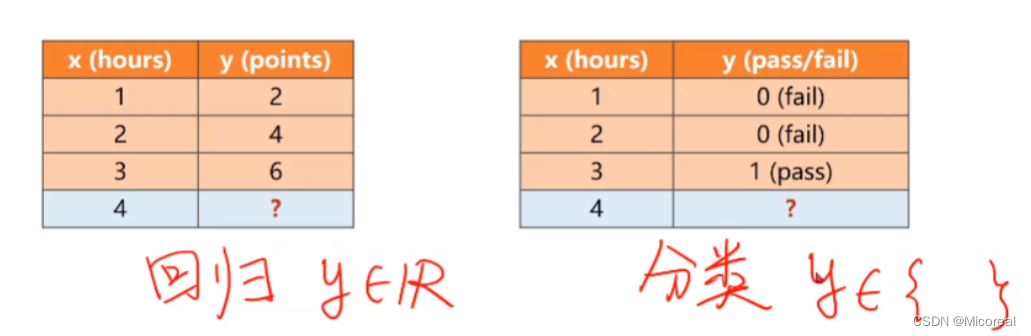
在之前提到的耗时效益的问题,是回归问题,也就是输入和输出间又数值上的关系。
| x | y |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | ? |
但如果,将 y y y的值记为是否合格,此问题变变换成一个(二)分类问题。
| x | y |
|---|---|
| 1 | fail(0) |
| 2 | fail(0) |
| 3 | pass(1) |
| 4 | pass |
实际上是计算在4工时下是否合格的概率,即对概率的计算与比较,而非类别之间的数值比较。
分类问题中,实际上是对概率的计算与比较,而非类别之间的数值比较.(也即离散问题时)
逻辑回归
二分类问题
二分类问题是非0即1的问题,由于隐藏条件的限制
P
(
y
^
=
1
)
+
P
(
y
^
=
0
)
=
1
P(\widehat y=1)+P(\widehat y=0) = 1
P(y
=1)+P(y
=0)=1
对于二分类问题结果的预测,仅需要计算在0或1的条件下即可得到答案。
通常计算
P
(
y
^
=
1
)
P(\widehat y=1)
P(y
=1)
逻辑函数
在原先的回归问题中,所利用的模型为
y
^
=
ω
x
+
b
\widehat y = \omega x+b
y
=ωx+b
此时的
y
^
∈
R
\widehat y \in R
y
∈R,但当问题为分类问题时,所求结果的值域应当发生改变,变为一个概率即
y
^
∈
[
0
,
1
]
\widehat y \in [0,1]
y
∈[0,1]
因此,需要引入逻辑函数(sigmod)来实现。
σ
(
x
)
=
1
1
+
e
−
x
\sigma(x) = \frac{1}{1+e^{-x}}
σ(x)=1+e−x1
本函数原名为logistics函数,属于sigmod类函数,由于其特性优异,代码中的sigmod函数就指的是本函数。其函数图像为
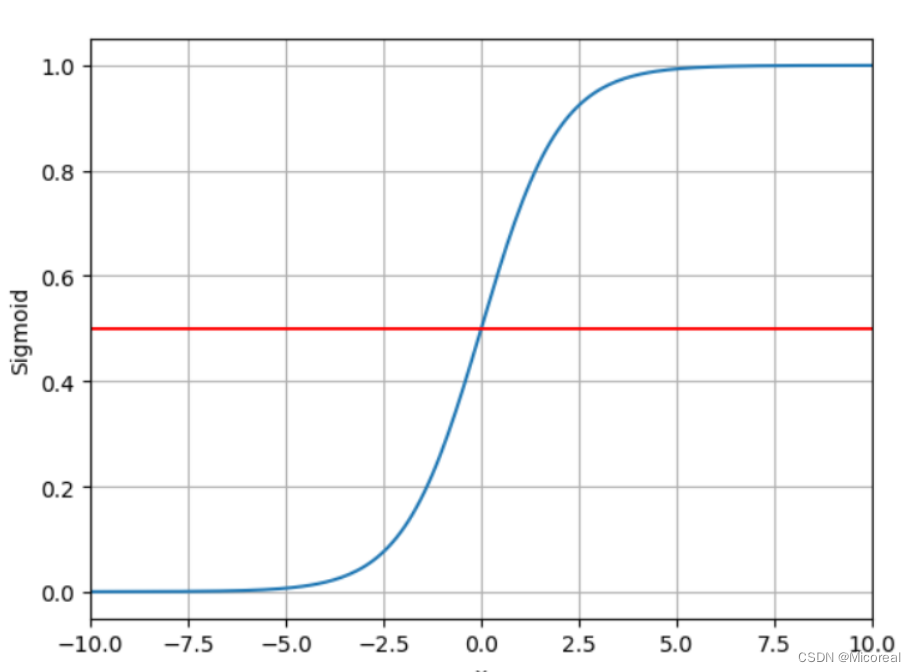
以及其他的sigmod函数:(但现在指向sigmod函数常指上面的那个函数)
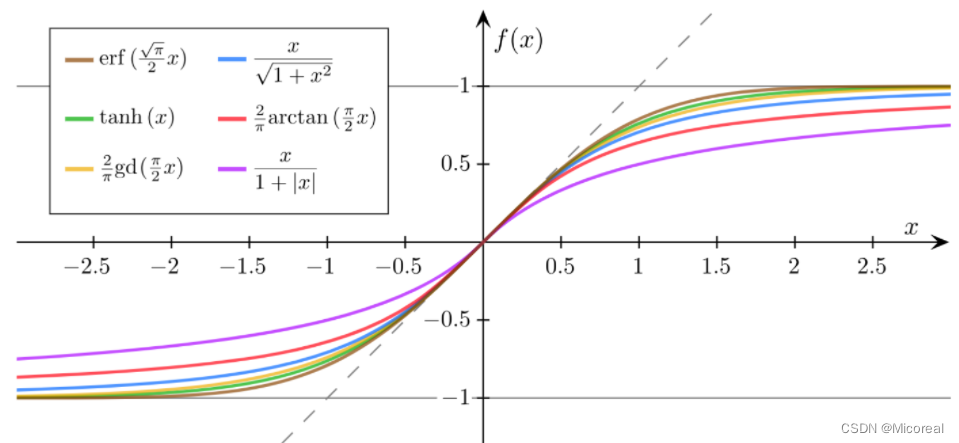
sigmod函数的特点:
- 函数值在0到1之间变化明显(导数大)
- 在趋近于0和1处函数逐渐平滑(导数小)
- 函数为饱和函数
- 单调增函数
与线性回归方程的不同
模型变化
线性函数后加上了sigmod函数

loss函数不同
损失函数由线性回归的MSE到BCE LossFunction

BCEloss函数的介绍
原先是计算两个标量数值间的差距,也就是数轴上的距离。
现在为了计算两个概率之间的差异,需要利用到交叉熵的理论。

交叉熵具体理解
简单的理解上,我们仅仅需要了解这个结论:
如下图所示,
y
^
\widehat y
y
与
y
y
y越接近,BCE Loss越小

课程代码
import torch.nn.functional as F
import torch
x_data = torch.Tensor([[1.0],[2.0],[3.0]])
y_data = torch.Tensor([[0.0],[0.0],[1.0]])
#改用LogisticRegressionModel 同样继承于Module
class LogisticRegressionModel(torch.nn.Module):
def __init__(self):
super(LogisticRegressionModel, self).__init__()
self.linear = torch.nn.Linear(1,1)
def forward(self, x):
#对原先的linear结果进行sigmod激活
y_pred = F.sigmoid(self.linear(x))
return y_pred
model = LogisticRegressionModel()
#构造的criterion对象所接受的参数为(y',y) 改用BCE
criterion = torch.nn.BCELoss(size_average=False)
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
for epoch in range(1000):
y_pred = model(x_data)
loss = criterion(y_pred,y_data)
print(epoch,loss)
optimizer.zero_grad()
loss.backward()
optimizer.step()
print('w = ', model.linear.weight.item())
print('b = ', model.linear.bias.item())
x_test = torch.Tensor([[4.0]])
y_test = model(x_test)
print('y_pred = ',y_test.data)
需要关注的是,此处的Tensor无法写成tensor,具体的区别:链接