一、实验目的

1、理解基本的二进制数字调制的原理；
2、理解ook、2FSK、2PSK信号时域波形和频谱的主要特点；
3、掌握上述matlab程序实现。

二、实验内容

用matlab产生独立等概的二进制信源，
1、画出OOK信号波形和功率谱；
2、画出2PSK信号波形和功率谱；
3、画出2FSK信号波形和功率谱

三、实验原理

1、二进制数字调制
数字调制：把数字基带信号变为数字带通信号的过程，有振幅调制，频移调制，相移调制三种。数字调制奇数有两种方法:①利用模拟调制的方法去是实现数式调制。②通过开关键控载波，称为键控法。
在这里插入图片描述
1.时域波形和频谱的主要特点
①OOK
在2ASK中，载波的幅度只有两种变化状态，分别对应二进制信息“0”或“1”。二进制振幅键控的表达式为：s(t) = A(t)cos(w0+θ) 0＜t≤T，式中，w0=2πf0为载波的角频率；A(t)是随基带调制信号变化的时变振幅，即在这里插入图片描述

其波形如下：在这里插入图片描述
②2FSK
二进制频移键控信号码元的“1”和“0”分别用两个不同频率的正弦波形来传送，而其振幅和初始相位不变。
故其表达式为

③2PSK
2PSK：载波的两种相位（0和π）去对应基带信号的“0”与“1”两种码元。因此二元数字调相就是让载波在两种相位间切换，故称相移键控。
二进制移相键控信号的典型时间波形如下图所示。
在这里插入图片描述

四、实验程序

clear all; 
close all;
clc;
M=10;                     %产生码元数    
L=100;                    %每码元复制L次
Ts=1;                 %每个码元的宽度,即码元的持续时间
Rb=1/Ts;                  %码元速率1
dt=Ts/L;                  %采样间隔
fs = 1/dt
TotalT=M*Ts;              %总时间
t=0:dt:TotalT-dt;         %时间
%% 产生单极性波形
wave=randi([0,1],1,M);    %产生二进制随机码,M为码元个数
fz=ones(1,L);             %定义复制的次数L,L为每码元的采样点数
x1=wave(fz,:);            %复制的第1行复制L次
%% 产生OOK
dnrz=reshape(x1,1,L*M);   %产生单极性不归零矩形脉冲波形
fc=2*Rb;                 %载波频率是基带信号的二倍。        
zb=sin(2*pi*fc*t);
ask2=dnrz.*zb;            %2ASK的模拟调制
%% 产生2FSK
kf=0.3;
sfm=modulate(dnrz,fc,fs,'fm',kf);
%% 产生2PSK
m1=[];
c1=[];
b1=[];
for i=1:M
      t1=(i-1)*Ts:dt:i*Ts-dt; 
        if wave(i)==0;
            m=ones(1,L);
            b=zeros(1,L);
        else wave(i)==1;
            m=-ones(1,L);
            b=ones(1,L);
        end
%通过循环方式对输入信号的进行赋值实现调制目的
        c=sin(2*pi*fc*t1);
        m1=[m1 m];
        c1=[c1 c];
        b1=[b1,b];
end
psk=c1.*m1;
%% 绘制OOK 2PSK 2FSK波形
figure(1);
subplot(411)
plot(t,dnrz)
title('单极性不归零矩形脉冲')
axis([0,TotalT,-0.1,1.1])
subplot(412)
plot(t,ask2);
title('OOK已调信号波形')
axis([0,TotalT,-1.1,1.1]);
subplot(413)
plot(t,sfm);
title('2FSK已调信号波形')
axis([0,TotalT,-1.1,1.1]);
subplot(414)
plot(t,psk)
title('2PSK已调信号波形')
axis([0,TotalT,-1.1,1.1]);
%% 频谱
T=t(end);%时间
df=1/T;%频率
N=length(ask2);%采样长度
f=(-N/2:N/2-1)*df;%采样频率
sf1=fftshift(abs(fft(ask2)));%对2ASK信号采用快速傅里叶变换并移到矩阵中心
sf2=fftshift(abs(fft(sfm)));%对2ASK信号采用快速傅里叶变换并移到矩阵中心
sf3=fftshift(abs(fft(psk)));%对2ASK信号采用快速傅里叶变换并移到矩阵中心
%% 画出频谱图
figure(2);
subplot(311)
plot(f,sf1)%画出调制信号频谱
title("OOK频谱")
subplot(312)
plot(f,sf2)%画出调制信号频谱
title("2FSK频谱")
subplot(313)
plot(f,sf3)%画出调制信号频谱
title("2PSK频谱")

五、实验结果与分析

1.OOK、2FSK和2PSK信号波形仿真结果：
在这里插入图片描述
2.OOK、2FSK和2PSK信号频谱仿真结果：

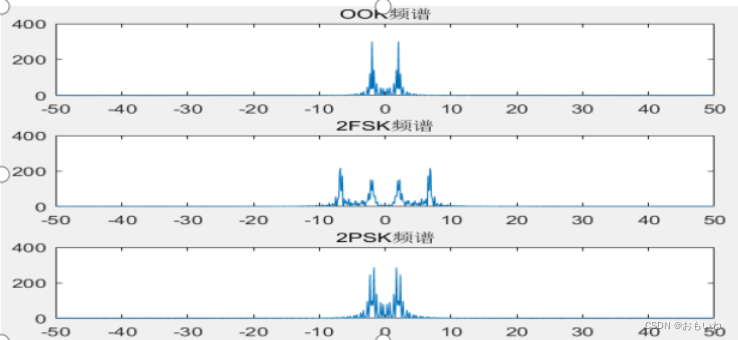
六、问题讨论

1.总结本实验的主要收获。
①对OOK，2PSK和2FSK的产生方法模拟调制法和键控法有了更深的理解和认识。
②对OOK，2PSK和2FSK的仿真频谱图进行分析，更深的理解了它们的频谱成分。
③掌握利用matlab进行傅里叶变换求信号频谱，对matlab编程更加的熟练。
2.对实验内容提出自己的想法和建议。
在此实验的基础上，我们可以进一步观察当基带信号在传输过程中存在噪声时，调制产生信号的波形，以及在接收端实现信号的解调，对仿真结果进行分析。