目录
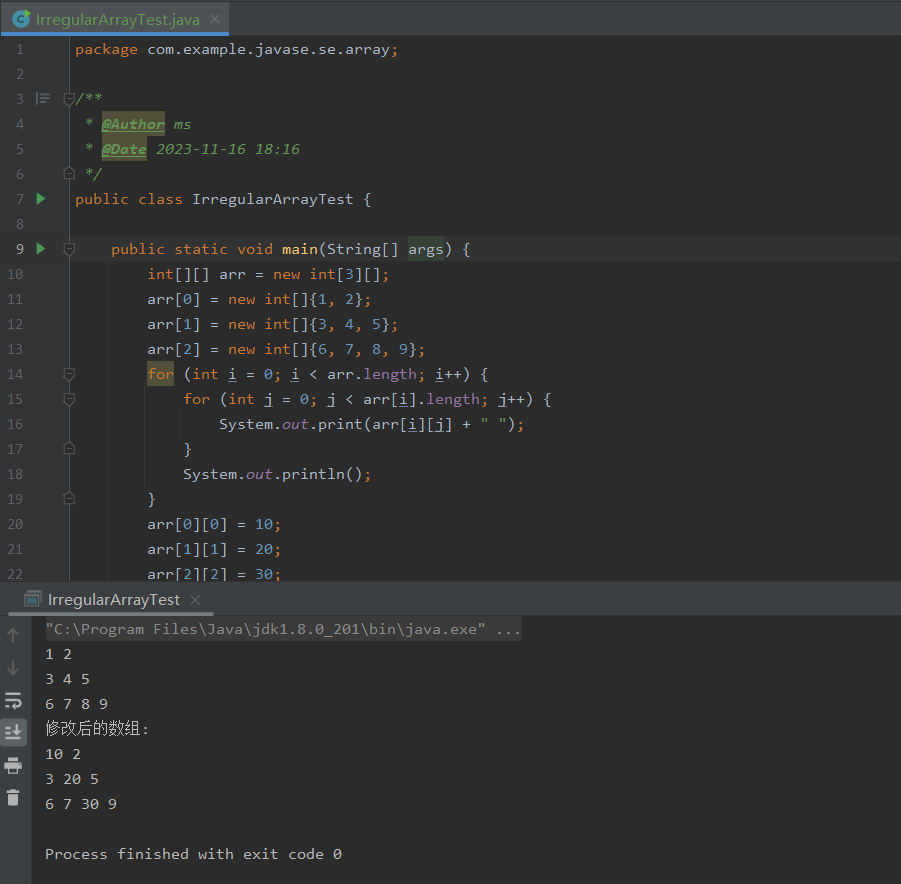
1.算法运行效果图预览
2.算法运行软件版本
3.部分核心程序
4.算法理论概述
5.算法完整程序工程
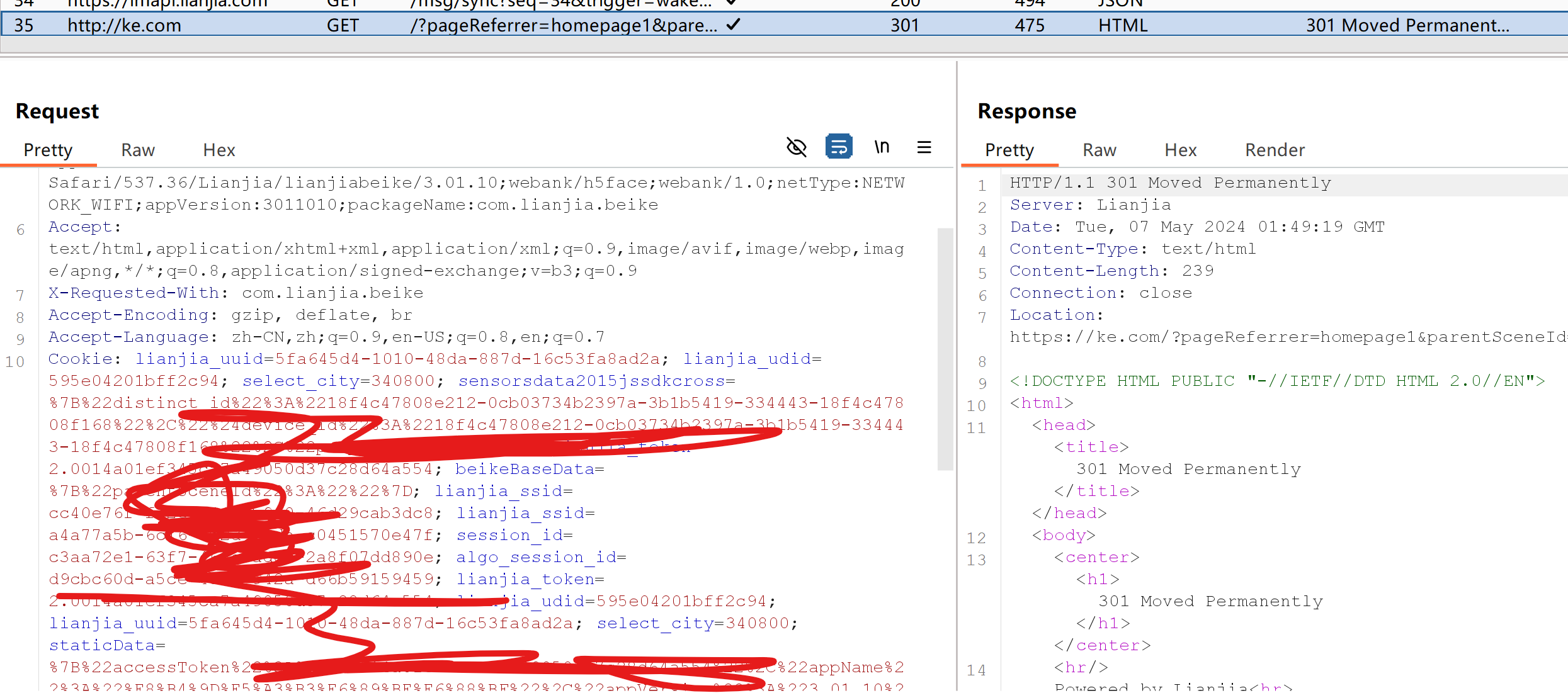
1.算法运行效果图预览
(完整程序运行后无水印)


2.算法运行软件版本
MATLAB2022a
3.部分核心程序
................................................................
while(Index<=Max_iteration)
Index
jj=1;
error2 = zeros(Len,KER);
while(jj<=Len)
for k=1:No;
d(k)=T(jj);
end
for i=1:NI;
x(i)=P(jj,i);
end
%集成多个BP神经网络
for bpj = 1:KER
for j=1:Nh%BP前向
net=0;
for i=1:NI
net=net+x(i)*W0(i,j,bpj); %加权和∑X(i)V(i)
end
y(j)=1/(1+exp(-net));
end
for k=1:No
net=0;
for j=1:Nh
net=net+y(j)*W(j,k,bpj);
end
%输出值
o(k)=1/(1+exp(-net));
end
RRR(jj,1) = round(o);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
errortmp=0.0;
for k=1:No
errortmp=errortmp+(d(k)-(o(k)))^2;%传统的误差计算方法
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
error2(jj,bpj)=0.5*errortmp/No;
for k=1:No%BP反向计算
yitao(k)=(d(k)-o(k))*o(k)*(1-o(k));%偏导
end
for j=1:Nh
tem=0.0;
for k=1:No
tem=tem+yitao(k)*W(j,k,bpj);
end
yitay(j)=tem*y(j)*(1-y(j));%偏导
end
for j=1:Nh%权值更新
for k=1:No
deltaW(j,k,bpj) = Learning_Rate*yitao(k)*y(j);
W(j,k,bpj) = W(j,k,bpj)+deltaW(j,k,bpj);
end
end
for i=1:NI
for j=1:Nh
deltaW0(i,j,bpj) = Learning_Rate*yitay(j)*x(i);
W0(i,j,bpj) = W0(i,j,bpj)+deltaW0(i,j,bpj);
end
end
end
jj=jj+1;
end
%BP训练结束
error = sum(mean(error2));
Index = Index+1;
ERR = [ERR,error];
end
.........................................................
05_035m4.算法理论概述
基于负相关误差函数(Negative Correlation Learning, NCL)的集成学习方法应用于BP(Backpropagation)神经网络,旨在通过训练多个相互独立且在预测上具有负相关的模型,提高整体模型的泛化能力和稳定性。这种方法结合了神经网络的强大表达能力和集成学习的思想,以提高预测精度和鲁棒性。
集成学习是机器学习领域的一种重要策略,它通过组合多个弱学习器来构建一个强学习器。NCL在集成学习框架下的应用,特别是与BP神经网络结合时,其核心思想是促使每个神经网络模型学习到不同的模式,从而减少整体模型之间的错误相关性。当模型间的预测错误呈现负相关时,即一个模型在某些样本上犯错时,其他模型能在这些样本上正确预测,整个集成系统的错误率会显著降低。
负相关误差函数的公式:
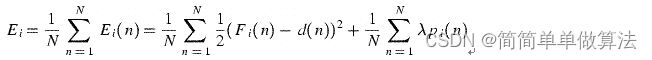
可知,当λ=0时,后面的惩罚项为0,相当于是网络单独训练,也就是传统的集成方式,当λ取大于0的值时为负相关集成,所以,以下对λ取值分别为0和其他值进行比较.
基于负相关误差函数的集成BP神经网络,通过鼓励模型间预测的负相关性,有效提升了模型的泛化能力。
5.算法完整程序工程
OOOOO
OOO
O