给定一个数组 A 和一些查询 Li,Ri，求数组中第 Li 至第 Ri 个元素之和。

小蓝觉得这个问题很无聊，于是他想重新排列一下数组，使得最终每个查询结果的和尽可能地大。

小蓝想知道相比原数组，所有查询结果的总和最多可以增加多少?

输入格式

输入第一行包含一个整数 n。

第二行包含 n 个整数 A1,A2,⋅⋅⋅,An，相邻两个整数之间用一个空格分隔。

第三行包含一个整数 m 表示查询的数目。

接下来 m 行，每行包含两个整数 Li、Ri，相邻两个整数之间用一个空格分隔。

输出格式

输出一行包含一个整数表示答案。

数据范围

对于 30% 的评测用例，n,m≤50；
对于 50% 的评测用例，n,m≤500；
对于 70% 的评测用例，n,m≤5000；
对于所有评测用例，1≤n,m≤10^5，1≤Ai≤10^6，1≤Li≤Ri≤n。

输入样例：

5
1 2 3 4 5
2
1 3
2 5

输出样例：

4

样例解释

原来的和为 6+14=20，重新排列为 (1,4,5,2,3) 后和为 10+14=24，增加了 4。

本题用到了排序不等式的概念

本题思路如下

 

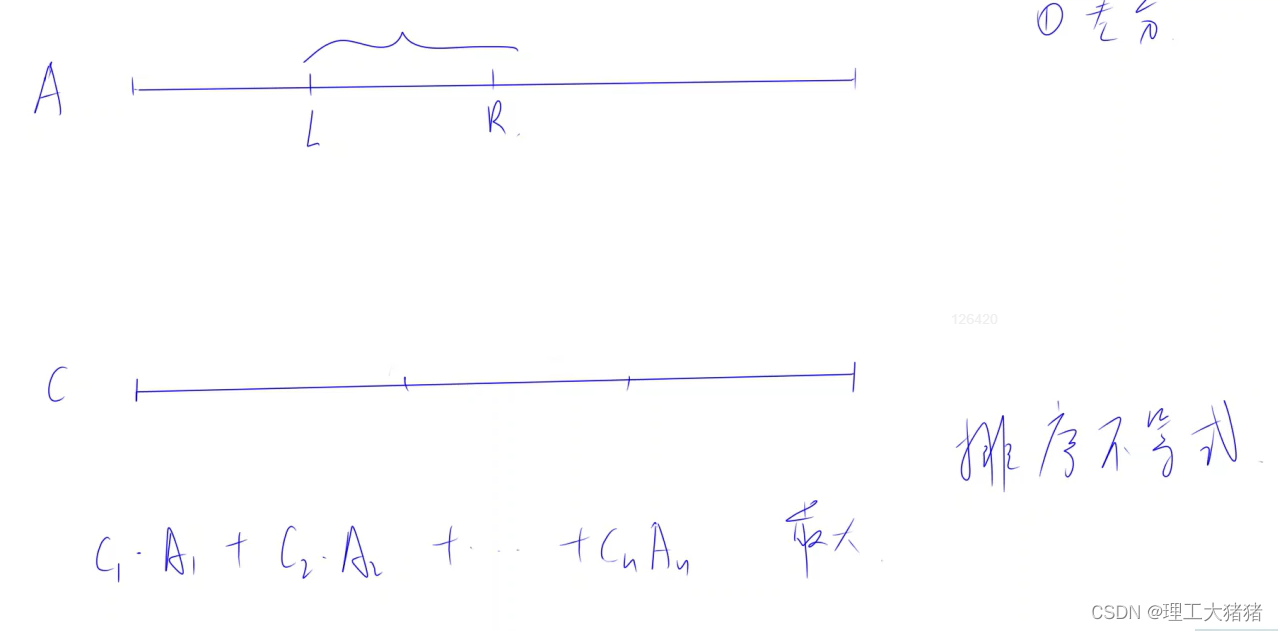
AC代码 

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;
const int N = 100010;
typedef long long LL;
int num[N], n, m, qz[N];
int main()
{
    cin >> n;
    for (int i = 1; i <= n; i ++ )   cin >> num[i];
    cin >> m;
    while (m -- ){
        int l, r;
        cin >> l >> r;
        qz[l] ++; qz[r + 1] --;
    }
    for (int i = 1; i <= n; i ++ )  qz[i] += qz[i - 1];
    LL sum1 = 0;
    for (int i = 1; i <= n; i ++ )
        sum1 += (LL)qz[i] * num[i];

    LL sum2 = 0;
    sort(num + 1, num + n + 1);
    sort(qz + 1, qz + n + 1);
    for (int i = 1; i <= n; i ++ )
        sum2 += (LL)qz[i] * num[i];

    cout << sum2 - sum1 << endl;
    return 0;
}