96. 不同的二叉搜索树
- 题目
- 算法设计:枚举
- 算法设计:动态规划
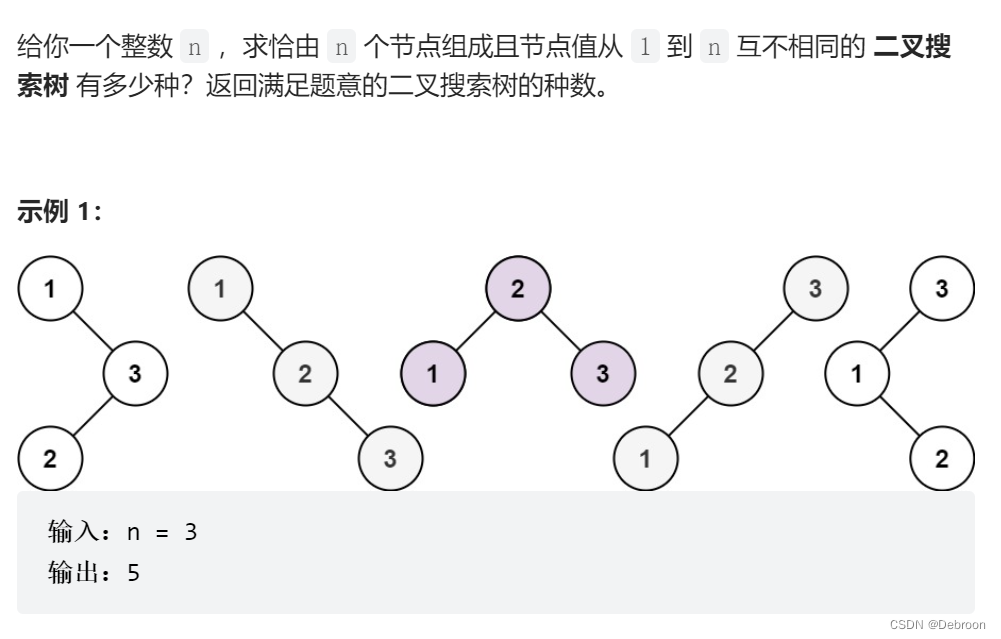
题目
传送门:https://leetcode.cn/problems/unique-binary-search-trees/
算法设计:枚举
当 n = 5,用 {1、2、3、4、5} BST数是多少组?
有 5 种情况,因为每个数字都可以作为根节点。
- 以 1 为根节点的BST数
- ······
- 以 5 为根节点的BST数
比如固定 3 作为根节点,这个前提下能有几种不同的 BST 呢?
根据 BST 的特性,根节点的左子树都比根节点的值小,右子树的值都比根节点的值大。
固定 3 作为根节点,左子树节点就是 {1,2}、{2,1} 的组合,右子树就是 {4,5}、{5、4} 的组合,2*2=4。
左子树的组合数和右子树的排列数乘积,就是 3 作为根节点时的 BST 个数。
class Solution {
public:
int numTrees(int n) {
if(n <= 1) return 1;
int ans = 0;
for(int i = 1; i <= n; i++)
ans += numTrees(i-1) * numTrees(n-i);
return ans;
}
};
缓存,减少子问题的计算:
class Solution {
public:
int dp[20];
int numTrees(int n) {
if(n <= 1) return 1;
if(dp[n]) return dp[n];
for(int i = 1; i <= n; i++)
dp[n] += numTrees(i-1) * numTrees(n-i);
return dp[n];
}
};
算法设计:动态规划
如果整数 1 ~ n 中的 k 作为根节点值,如 n = 3 时,k = 1、2、3:
- 1 为根节点时BST数量
- 2 为根节点时BST数量
- 3 为根节点时BST数量
- 定义状态 dp[i],为 i 为根节点时BST数量
那 dp[i] 从哪里来?
- 分析原理:https://leetcode.cn/problems/unique-binary-search-trees/solution/buton-by-ao-zi-ge-pilg/
class Solution {
public:
int numTrees(int n) {
vector<int> dp(n + 1);
dp[0] = 1;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= i; j++)
dp[i] += dp[j - 1] * dp[i - j];
return dp[n];
}
};