代码随想录--二叉树章节总结 Part II

代码随想录–二叉树章节总结 Part II

1.Leetcode222 求完全二叉树结点的个数

给你一棵完全二叉树的根节点 root ，求出该树的节点个数。

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

解题思路1：利用递归，按照普通的二叉树去处理

public int countNodes(TreeNode root) {
    if (root == null) return 0;
    if (root.left == null && root.right == null)
      return 1;
    // 计算左子树的元素个数
    // 计算右子树的元素个数
    // 以root为根的子树的元素个数 = 左 + 右 + 1 这个1就是root结点
    int left = countNodes(root.left);
    int right = countNodes(root.right);
    return left + right + 1;
}

解题思路2: 利用层序遍历，按照普通的二叉树去处理

public int countNodes(TreeNode root) {
    if (root == null) return 0;
    if (root.left == null && root.right == null)
      return 1;
    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root);
    int count = 0;
    while (!queue.isEmpty()) {
        TreeNode node = queue.poll();
        count++;
        if (node.left != null) queue.offer(node.left);
        if (node.right != null) queue.offer(node.right);
    }
    return count;
}

解题思路3：利用递归，结合完全二叉树的性质去做。

首先去要明确一下完全二叉树的性质

一个n层的完全二叉树，n-1层都是满二叉树
n层的满二叉树，他的结点个数为 $2^n-1$

思路如下：

我们可以递归的去判断某一个结点为根的子树是不是满二叉树，如果是满二叉树，则直接使用公式计算即可。
如果不是满二叉树，那就继续递归，判断这个结点的左右子树是不是满二叉树，最终到叶子结点，叶子结点一定是满二叉树

那么如何判断一个树是满二叉树呢，这里的前提是这个树一定是完全二叉树

我们可以从根结点开始遍历，一个指针一致沿着这个树的左边走，另一个一致沿着这个树的右边走，如果到达叶子后，这两个经过的深度不一致，则说明不是满二叉树。

有人可能会提出下面这种树，说满足左右经过深度相同，但是不一定是满二叉树，这个需要注意的是我们的前提是这个树一定是完全二叉树，下面的这个例子中的树并不是完全二叉树。

具体思路

如果传入结点是空结点，返回0
如果传入结点是叶子结点。返回1
然后创建两个指针，分别沿着左边和右边进行遍历了，直到叶子结点位置。判断两个指针经过的深度是否相同，如果相同，则直接返回根据公式计算的满二叉树结点数
如果不相同，则递归的判断左子树和右子树，求结点数量，最后+1返回

public static int countNodes(TreeNode root) {
    if (root == null) return 0;
    if (root.left == null && root.right == null) return 1;
    // 创建两个指针
    TreeNode curLeft = root.left;
    TreeNode curRight = root.right;
    int countLeft = 0, countRight = 0;
    while (curLeft != null) {
        curLeft = curLeft.left;
        countLeft++;
    }
    while (curRight != null) {
        curRight = curRight.right;
        countRight++;
    }
    if (countRight == countLeft)
      	return (2 << countRight) - 1; // 2 << 1 相当于 2*2

    // 后序
    int left = countNodes(root.left);
    int right = countNodes(root.right);

    return left + right + 1;
}

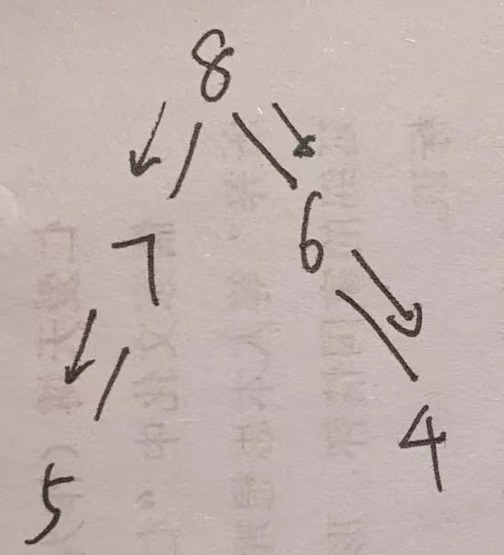
图解过程：

2.Leetcode110 平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1 。

解题思路1： 利用后序遍历递归判断。先判断根结点是不是平衡二叉树，如果根结点是平衡二叉树则继续判断左右子树是不是平衡二叉树。

为什么是后序遍历，因为最后这个根结点是不是平衡二叉树取决于左右子树是不是平衡二叉树所以是左右根
return isBalanced(root.left) && isBalanced(root.right);

public boolean isBalanced(TreeNode root) {
    if (root == null) return true;
        if (root.left == null && root.right == null) return true;

        // 后序遍历，先判断左子树是不是平衡二叉树 如果不是直接返回false
        // 左
        boolean left = isBalanced(root.left);
        if (!left) return false;
        // 右
        boolean right= isBalanced(root.right);
        if (!right) return false;
        // 中 说明左右子树都是平衡二叉树，现在判断根是不是
        if (Math.abs(getDepth(root.left) - getDepth(root.right)) <= 1) {
            return true;
        } else {
            return false;
        }
    }
}
private int getDepth(TreeNode node) {
    if (node == null) return 0;
    if (node.left == null && node.right == null) return 1;
    return Math.max(getDepth(node.left), getDepth(node.right)) + 1;
}

3.Leetcode257 二叉树所有路径

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。叶子节点 是指没有子节点的节点。

输入：root = [1,2,3,null,5]
输出：["1->2->5","1->3"]

输入：root = [1]
输出：["1"]

解题思路1：我们可以使用层序遍历。使用两个队列来记录，一个队列用来实现层序遍历，另一个队列用来记录经过的路径。当遍历到叶子结点的时候, 就把路径保存带list中。

public static List<String> binaryTreePaths(TreeNode root) {
      ArrayList<String> list = new ArrayList<>();
      if (root == null) return list;
      // 创建两个队列
      Queue<TreeNode> QNode = new LinkedList<>();
      Queue<StringBuilder> QPath = new LinkedList<>();
      // 根结点进队
      QNode.offer(root);
      QPath.offer(new StringBuilder().append(root.val));
      while (!QNode.isEmpty()) {
          // 出队
          TreeNode node = QNode.poll();
          StringBuilder poll = QPath.poll();
          // 这个if不要忘记判断！！！！！
          if (node.left == null && node.right == null) {
              // 如果是叶子结点，则直接保存到list中
              list.add(poll.toString());
          }
          if (node.left != null) {
              QNode.offer(node.left);
              QPath.offer(new StringBuilder(poll).append("->").append(node.left.val));
          }
          if (node.right != null) {
              QNode.offer(node.right);
              QPath.offer(new StringBuilder(poll).append("->").append(node.right.val));
          }
      }
      // 上面循环结束以后，QPath里面保存了根到所有叶子结点的路径
      return list;
}

图解上述方法：

解题思路2: 利用递归的方式进行前序遍历，记录路径。

从理论上说，这个代码应该包含回溯的内容，但是因为使用了String来记录，String是常量，所以不需要回溯。我还使用了StringBuilder进行测试，发现如果不回溯，会出问题。

public List<String> binaryTreePaths(TreeNode root) {
    ArrayList<String> list = new ArrayList<>();
    if (root == null) return list;
    String path = "";
    f(root, list, path);

    return list;
}

private void f(TreeNode node, ArrayList<String> list, String path) {
    path = path + "->" + String.valueOf(node.val);
    // 如果node是叶子结点
    if (node.left == null && node.right == null) {
      	list.add(path.substring(2, path.length())); // 去掉最开始的->
      	return;
    }
    // 如果不是叶子，则继续访问左右子树
    if (node.left != null) {
      	f(node.left, list, path);
    }
    if (node.right != null) {
      	f(node.right, list, path);
    }
}

下面展示使用回溯的方式

public List<String> binaryTreePaths(TreeNode root) {
    List<String> res = new ArrayList<>();
    if (root == null) {
      return res;
    }
    List<Integer> paths = new ArrayList<>();
    traversal(root, paths, res);
    return res;
}

private void traversal(TreeNode root, List<Integer> paths, List<String> res) {
    paths.add(root.val);
    // 叶子结点
    if (root.left == null && root.right == null) {
        // 输出
        StringBuilder sb = new StringBuilder();
        for (int i = 0; i < paths.size() - 1; i++) {
          	sb.append(paths.get(i)).append("->");
        }
        sb.append(paths.get(paths.size() - 1));
        res.add(sb.toString());
        return;
    }
    if (root.left != null) {
        traversal(root.left, paths, res);
        paths.remove(paths.size() - 1);// 回溯
    }
    if (root.right != null) {
        traversal(root.right, paths, res);
        paths.remove(paths.size() - 1);// 回溯
    }
}

4.Leetcode404 左叶子之和

给定二叉树的根节点 root ，返回所有左叶子之和。

示例 1：
输入: root = [3,9,20,null,null,15,7] 
输出: 24 
解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

示例 2:
输入: root = [1]
输出: 0

解题思路1： 利用递归遍历，先序遍历，判断结点是否是左叶子，如果是记录，否则继续遍历左右子树

public int sumOfLeftLeaves(TreeNode root) {
  // 如果只有一个结点，返回0
    if (root.left == null && root.right == null) return 0;
    int sum = 0;
    f(root, sum);
    return sum;
}
private void f(TreeNode node, int sum) {
    if (node.left != null && node.left.left == null && node.left.right == null) {
      	sum += node.left.val;
    } else {
        if (node.left != null)
          	f(node.left, sum);
        if (node.right != null)
          	f(node.right, sum);
    }
}

这个题里面判断叶子是不是左叶子，需要从他的父结点开始判断

首先是遍历到的这个结点他的左孩子不为空，其次是左孩子的左右结点为空，那么这个结点的左孩子就是左叶子

解题思路2: 利用迭代方式。使用了前序遍历。每遍历一个元素，就判断他是不是有左叶子，如果有则记录下来。

public int sumOfLeftLeaves(TreeNode root) {
    // 如果树为空，或者树中只有一个结点
    if (root == null || (root.left == null && root.right == null)) return 0;
    Stack<TreeNode> stack = new Stack<>();
    stack.push(root);
    int sum = 0;
    while (!stack.isEmpty()) {
        TreeNode node = stack.pop();
        if (node.left != null && node.left.left != null && node.left.right != null) {
          	sum += node.left.val;
        }
        if (node.right != null)
          	stack.push(node.right);
        if (node.left != null)
          	stack.push(node.left);
    }
    return sum;
}

5.Leetcode513 求树左下角的值

给定一个二叉树的根节点 root，请找出该二叉树的最底层最左边节点的值。

假设二叉树中至少有一个节点。

示例 1:
输入: root = [2,1,3]
输出: 1

示例 2:
输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7

解题思路1：利用层序遍历。每遍历一层，都记录着一层中被遍历到的第一个元素（覆盖）。最后返回结果即可。

public int findBottomLeftValue(TreeNode root) {
    if (root == null) return 0;
    // 首先获取到最大深度
    // 通过层序遍历
    Queue<TreeNode> queue = new LinkedList<>();
    int result = 0;
    queue.offer(root);
    while (!queue.isEmpty()) {
        int size = queue.size();
        for (int i = 0; i < size; i++) {
            TreeNode node = queue.poll();
            if (i == 0) result = node.val;
            if (node.left != null) queue.offer(node.left);
            if (node.right != null) queue.offer(node.right);
        }
    }
    return result;
}

6.Leetcode112 路径总和

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

解题思路1：层序遍历。我们可以使用层序遍历。使用两个队列来记录，一个队列用来实现层序遍历，另一个队列用来记录经过的路径。当遍历到叶子结点的时候，根据其路径求和来判断结果是不是target即可。

public boolean hasPathSum(TreeNode root, int targetSum) {
    // 处理树为空
    // 处理树为空
    if (root == null) return false;
    // 处理只有一个结点的情况
    if (root.left == null && root.right == null && root.val == targetSum)
      	return true;
    else if (root.left == null && root.right == null && root.val != targetSum)
      	return false;

    // 创建队列
    Queue<TreeNode> QNode = new LinkedList<>();
    Queue<ArrayList<Integer>> QPath = new LinkedList<>();
    // 入队
    QNode.offer(root);
    QPath.offer(new ArrayList<>(Arrays.asList(root.val)));


    // 开始遍历
    while (!QNode.isEmpty()) {
        TreeNode node = QNode.poll();
        ArrayList<Integer> path = QPath.poll();
        if (node.left != null) {
            QNode.offer(node.left);
            ArrayList<Integer> left = new ArrayList<>(path);
            left.add(node.left.val);
            QPath.offer(left);
        }
        if (node.right != null) {
            QNode.offer(node.right);
            ArrayList<Integer> right = new ArrayList<>(path);
            right.add(node.right.val);
            QPath.offer(right);
        }
        if (node.right == null && node.left == null) {
            // 如果是叶子结点，则path里面存储的就是从根结点到叶子接待的路径
            int sum = 0;
            for (Integer integer : path) {
              	sum += integer;
            }
            if (sum == targetSum) return true;
        }
    }
    return false;
}

这个题我们可以在遍历到叶子的时候，将path保存起来，这样就变成了保存满足taget的所有路径问题

图解如下：

解题思路2: 利用递归。这里采用的是前序遍历。

如果一个树是空树，则直接返回false
如果遍历到当前结点是叶子，那就需要计算是不是等于0，如果等于0，则返回true。否则返回false
如果遍历到当前结点不是叶子，则需要递归的去遍历左右子树。同时执行target-当前结点的val

public boolean hasPathSum(TreeNode root, int targetSum) {
    // 如果是空树
    if (root == null) return false;

    // 处理根结点
    if (root.left == null && root.right == null) {
        // 如果是叶子结点，则判断是否满足条件
        if (targetSum - root.val == 0) {
          	return true; // 满足返回true
        } else {
          	return false; // 不满足返回false
        }
    } else {
        // 如果不是叶子结点，则继续递归遍历左右子树
        return hasPathSum(root.left, targetSum - root.val) || hasPathSum(root.right, targetSum - root.val);
    }
}

7.Leetcode113 路径总和II

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

解题思路1: 层序遍历法，和上面的思路一样，这里就不再重复了。代码如下：

public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
    List<List<Integer>> list = new ArrayList<>();
    if (root == null) return list;

    // 创建两个队列
    Queue<TreeNode> nodeQ = new LinkedList<>();
    Queue<List<Integer>> pathQ = new LinkedList<>();

    // 根结点入队
    nodeQ.offer(root);
    pathQ.offer(new ArrayList<>(Arrays.asList(root.val)));

    // 开始循环
    while (!nodeQ.isEmpty()) {
        // 出队
        TreeNode node = nodeQ.poll();
        List<Integer> path = pathQ.poll();

        if (node.left != null) {
            nodeQ.offer(node.left);
            List<Integer> left = new ArrayList<>(path);
            left.add(node.left.val);
            pathQ.add(left);
        }

        if (node.right != null) {
            nodeQ.offer(node.right);
            List<Integer> right = new ArrayList<>(path);
            right.add(node.right.val);
            pathQ.add(right);
        }
        // 如果遍历的结点是叶子结点
        if (node.left == null && node.right == null) {
            // 计算结点和
            int sum = 0;
            for (Integer integer : path) {
              	sum += integer;
            }
            if (sum == targetSum)
              	list.add(path);
        }
    }
    return list;
}