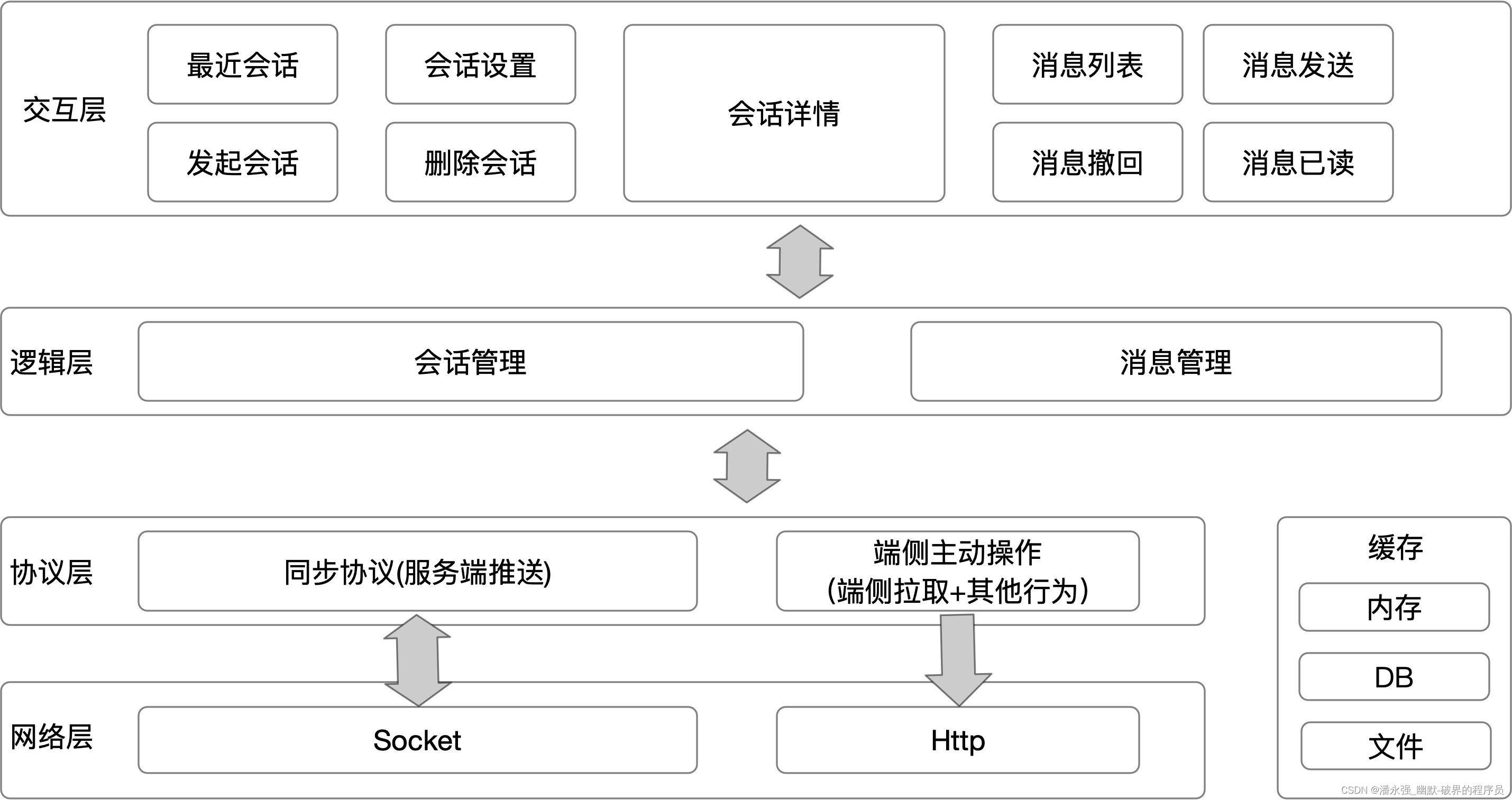
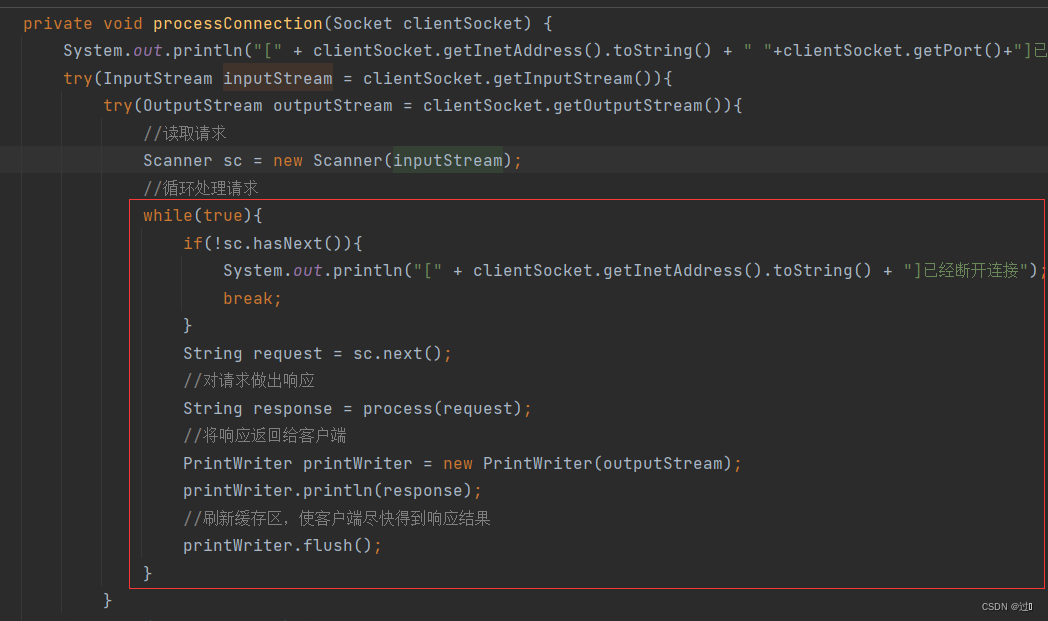
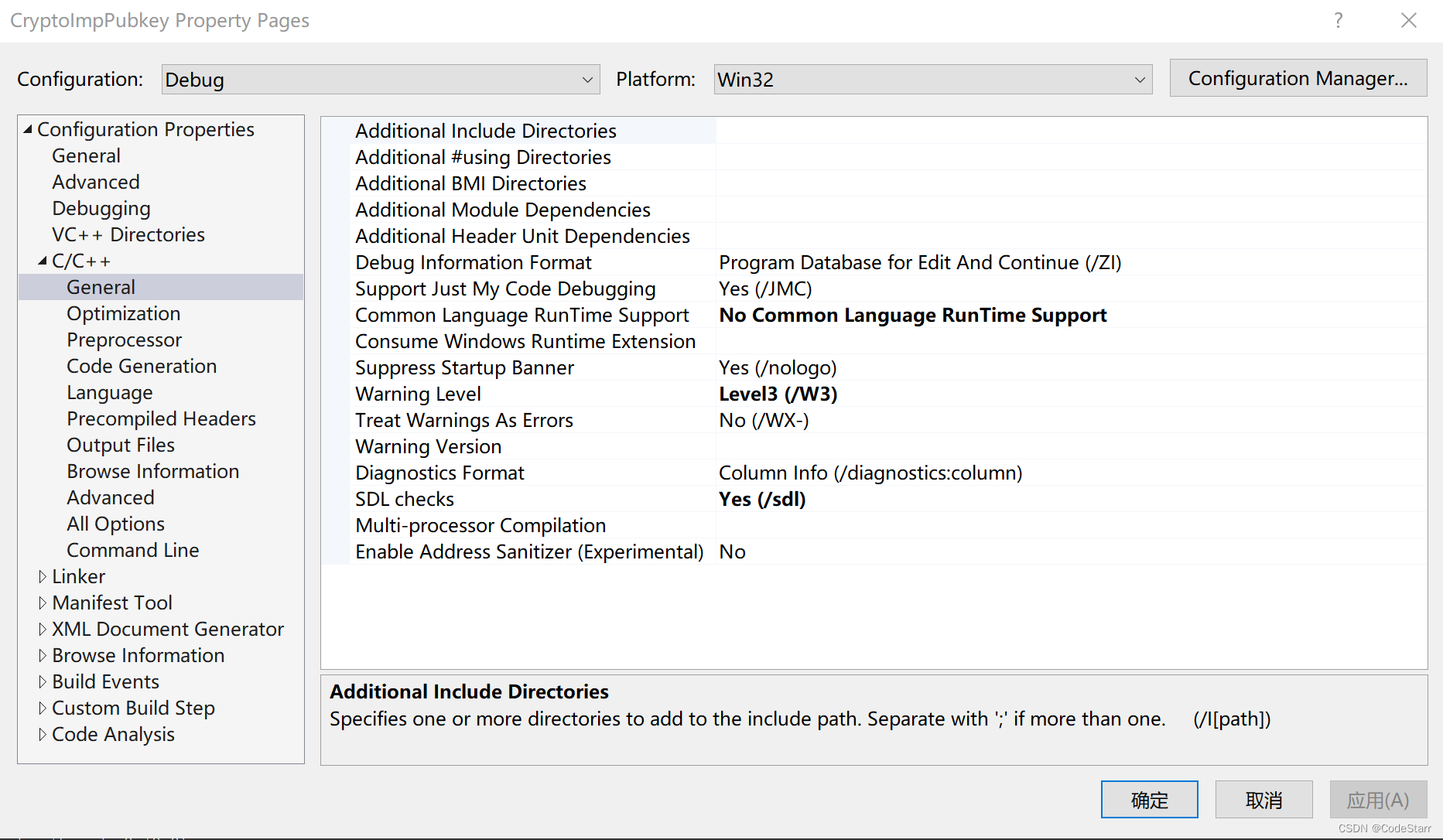
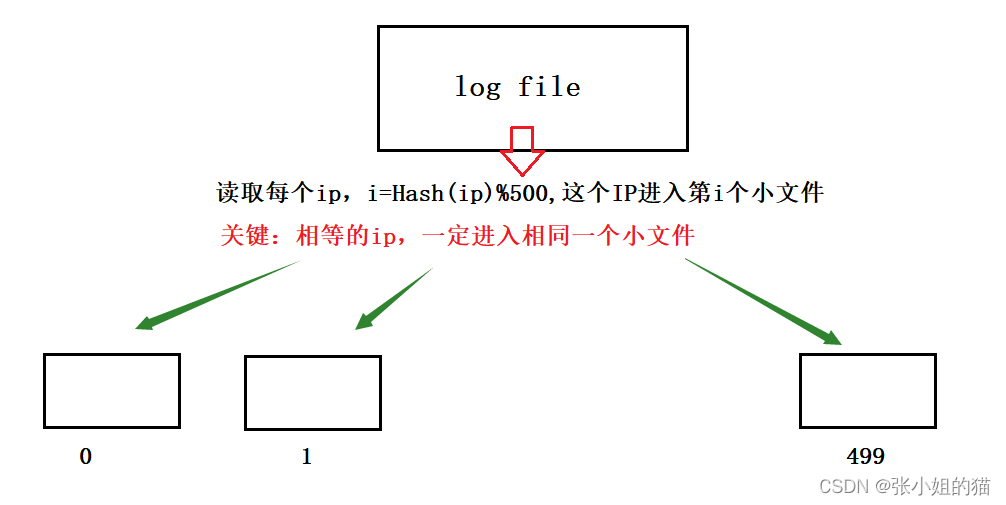
🌕 特征变换
特征变换主要就是针对一个特征,使用合适的方法,对数据的分布、尺度等进行变换,以满足建模时对数据的需求。
特征变换可分为数据的数据的无量纲化处理和数据特征变换。
🌗 数据的无量纲化处理
常用处理方法有:数据标准化、数据缩放、数据归一化等。
下面使用一个数据集进行演示。
import pandas as pd
data = pd.read_csv("D:/Pycharm/MachineLearning/program/data/chap2/Iris.csv")
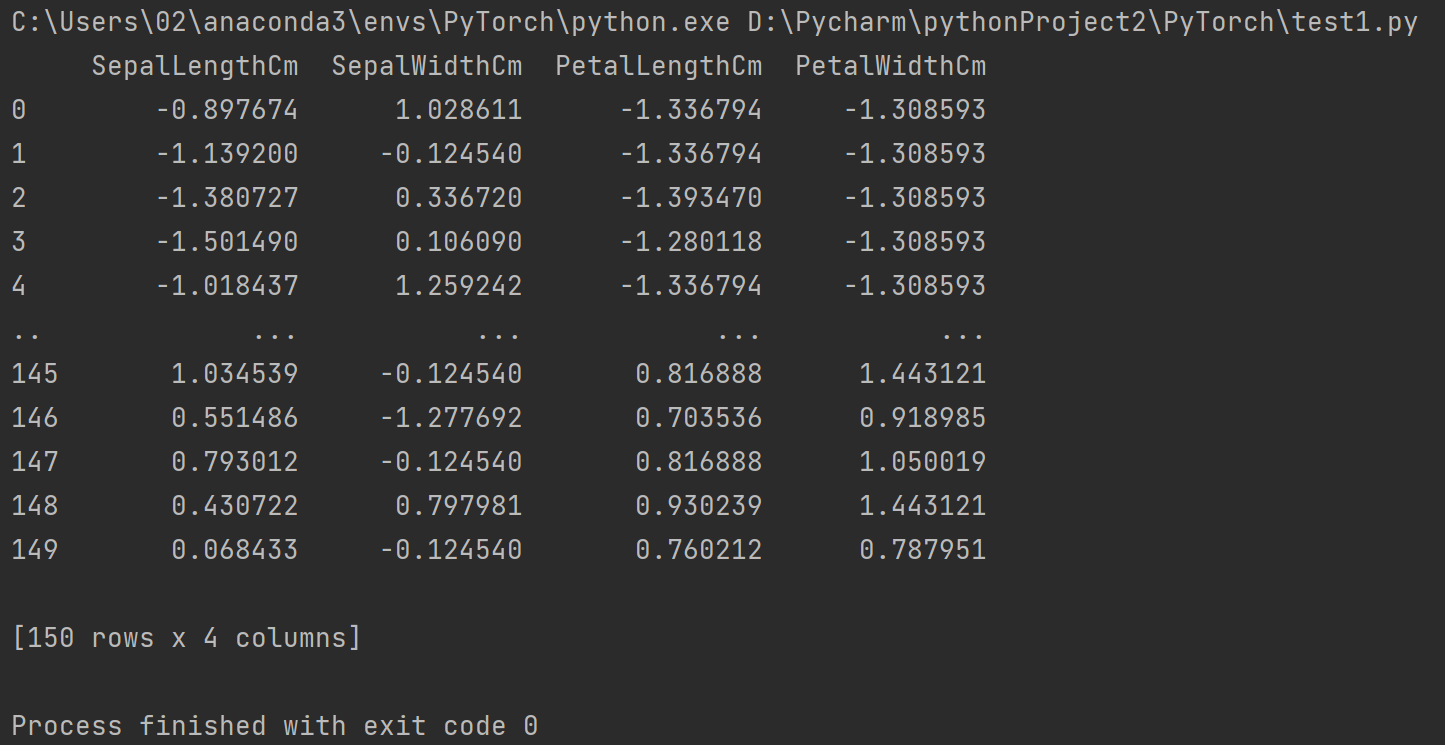
print(data)
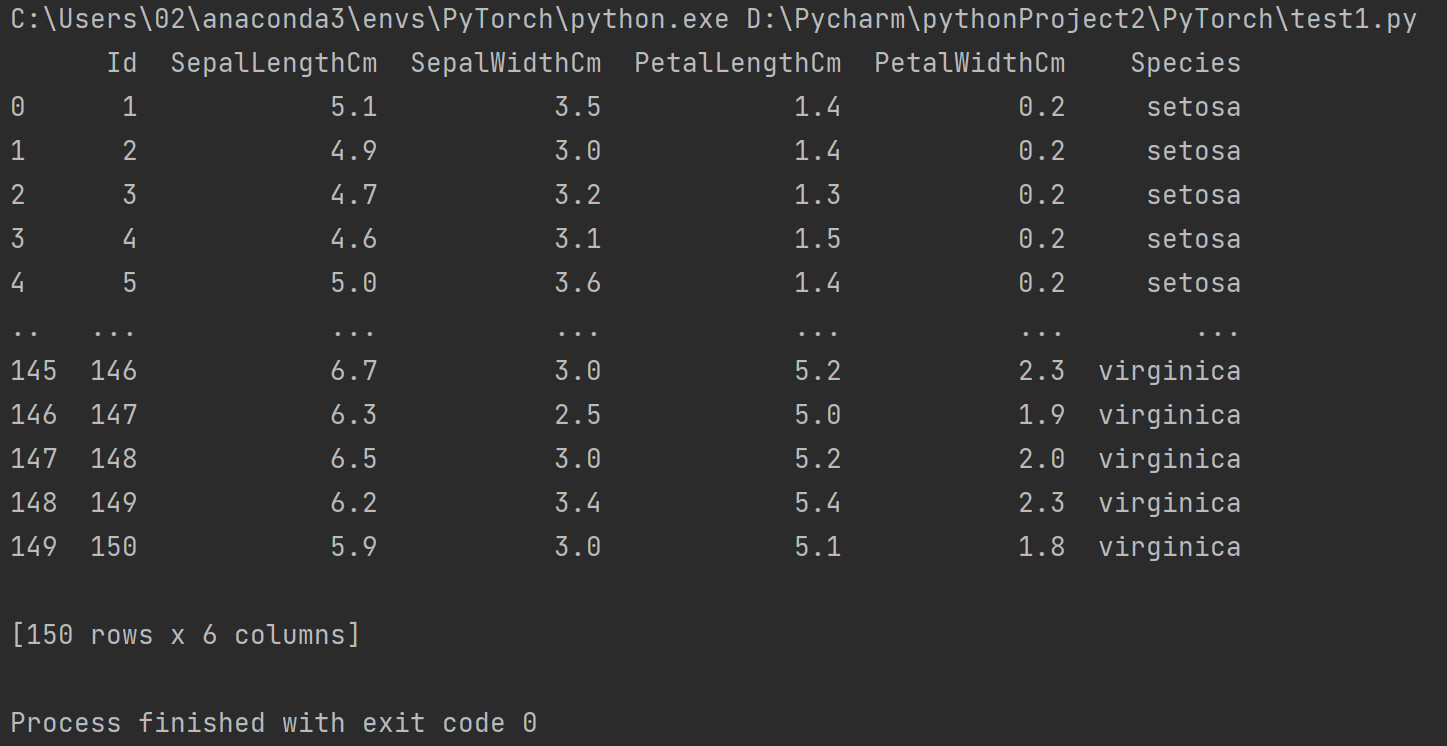
这里我们再去除“Id”列和“Species”列(因为数据的无量纲化只用数值就好)
import pandas as pd
data = pd.read_csv("D:/Pycharm/MachineLearning/program/data/chap2/Iris.csv")
data = data.drop(["Id","Species"],axis = 1)
print(data)
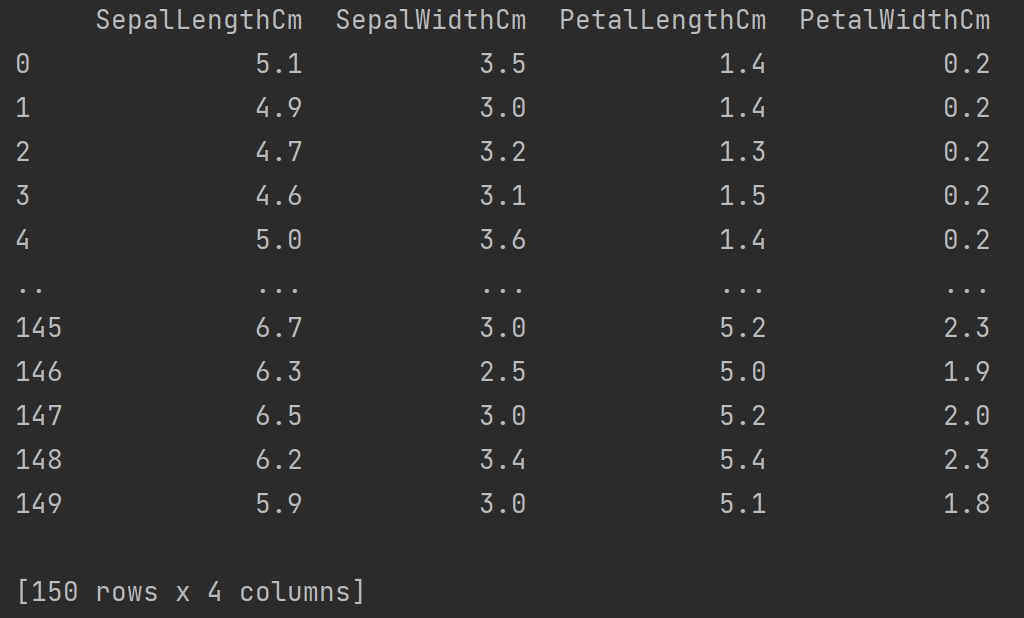
🌑 数据标准化
数据变量x标准化的公式为 x ′ = x − m e a n ( x ) s t d ( x ) x{'}=\frac{x-mean(x)}{std(x)} x′=std(x)x−mean(x),mean(x)为x的均值,std(x)为x的标准差,即每个数值减去变量的均值后再除以标准差。
import pandas as pd
data = pd.read_csv("D:/Pycharm/MachineLearning/program/data/chap2/Iris.csv")
data = data.drop(["Id","Species"],axis = 1)
data = (data - data.mean()) / data.std()
print(data)
在这里我们还可以使用sklearn库中preprocessing模块的scale()和StandardScaler()函数来完成,可以通过参数with_mean和with_std来控制是否减去均值和是否除以标准差。下面使用箱线图进行可视化分析:
# 导入相关的库
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import preprocessing
# 中文显示问题
import matplotlib
matplotlib.rcParams['axes.unicode_minus']=False
import seaborn as sns
sns.set(font="Kaiti",style="ticks",font_scale=1.4)
data = pd.read_csv("D:/Pycharm/MachineLearning/program/data/chap2/Iris.csv")
data = data.drop(["Id","Species"],axis = 1)
data_scale1 = preprocessing.scale(data,with_mean = True,with_std = True) # 使用scale函数标准化
data_scale2 = preprocessing.StandardScaler(with_mean = True,with_std = True).fit_transform(data) # 使用StandardScale函数标准化
labs = ['SepalL','SepalW','PetalL','PetalW'] # 可用labs=data.columns.values获取列名,我这里重命名是因为原列名太长,列名之间会交错出现。
plt.figure(figsize = (14,6))
plt.subplot(1,3,1) # 将画布分为1行3列3部分,现在对从左到右从上到下第1个图进行绘制
plt.boxplot(data.values,notch = True,labels = labs)
plt.grid()
plt.title("原始数据")
plt.subplot(1,3,2) # 对第2个图进行绘制
plt.boxplot(data_scale1,notch = True,labels = labs)
plt.grid()
plt.title("第一种形式标准化")
plt.subplot(1,3,3) # 对第3个图进行绘制
plt.boxplot(data_scale2,notch = True,labels = labs)
plt.grid()
plt.title("第二种形式标准化")
plt.subplots_adjust(wspace = 0.1) # 调整每个图形间的间距
plt.show()
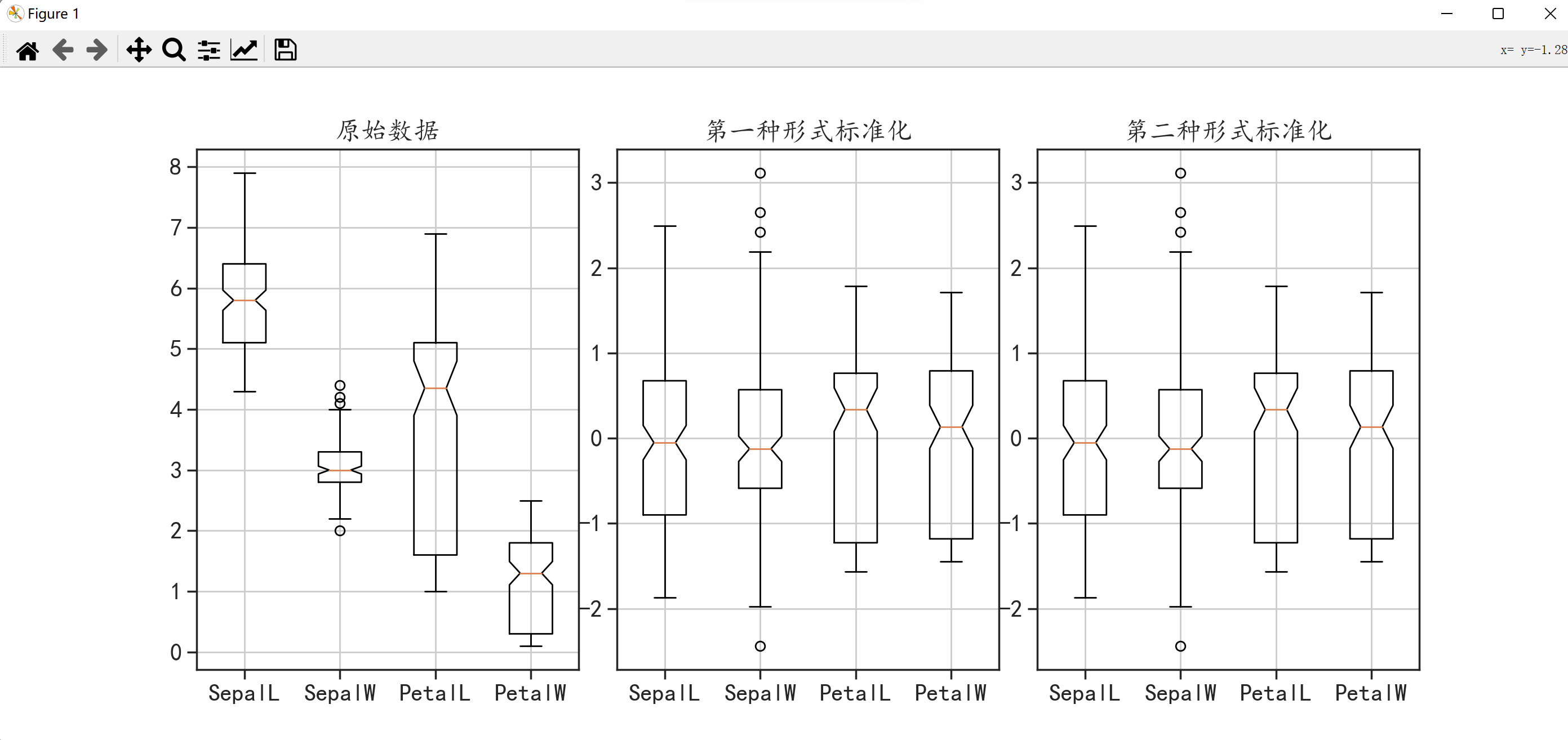
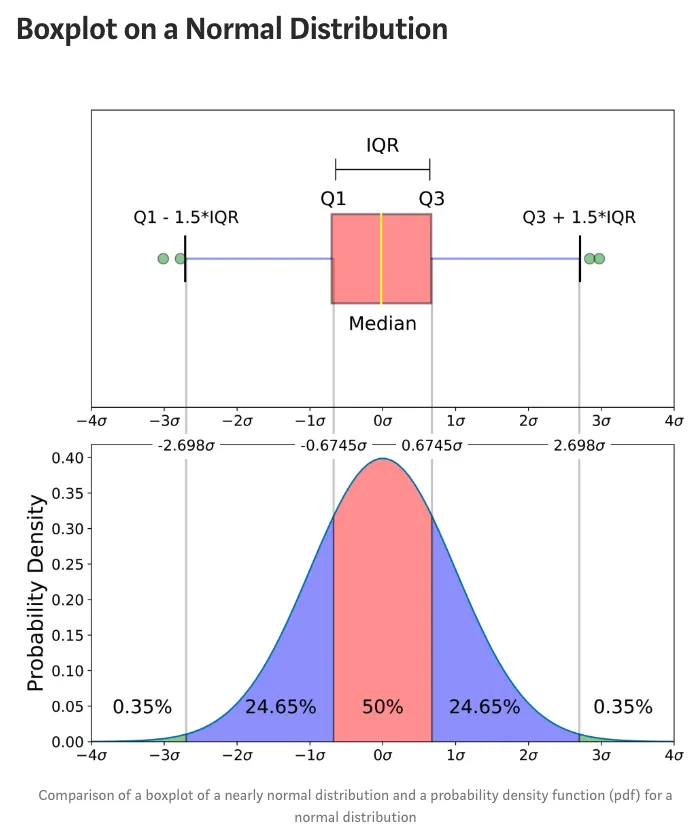
??上面这个图是个啥?这个怎么看?
先看下面这个图
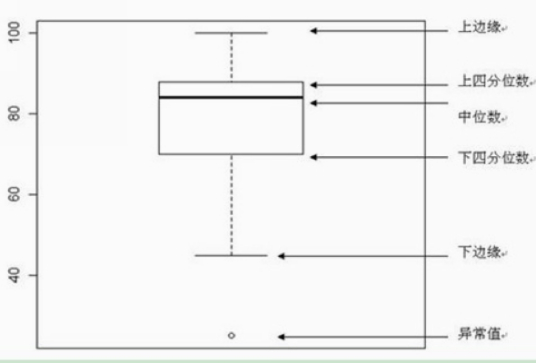
也许你看了还是会感到迷惑,但如果我们将它横过来看一下:

因为正态分布里也有中位数、上四分位数和下四分位数,所以我们就可以将其结合起来看,如下图:
图片来自知乎博主:jinzhao → \rightarrow →原文链接
这样一对比,应该就好理解了,把箱线图当成正态分布图来理解就行了。
🌑 数据缩放
数据缩放的计算公式位: x ′ = x − m i n ( x ) m a x ( x ) − m i n ( x ) x^{'}=\frac{x-min(x)}{max(x)-min(x)} x′=max(x)−min(x)x−min(x),它可以将数据缩放到指定的范围。可以用preprocessing模块中的MinMaxScale()函数来完成,并且可以使用feature_range参数指定缩放的范围。
# 导入相关的库
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import preprocessing
# 中文显示问题
import matplotlib
matplotlib.rcParams['axes.unicode_minus']=False
import seaborn as sns
sns.set(font="Kaiti",style="ticks",font_scale=1.4)
data = pd.read_csv("D:/Pycharm/MachineLearning/program/data/chap2/Iris.csv")
data = data.drop(["Id","Species"],axis = 1)
data_minmax1 = preprocessing.MinMaxScaler(feature_range = (0,1)).fit_transform(data)
data_minmax2 = preprocessing.MinMaxScaler(feature_range = (1,10)).fit_transform(data)
labs = ['SepalL','SepalW','PetalL','PetalW']
plt.figure(figsize = (25,6))
plt.subplot(1,3,1)
plt.boxplot(data.values,notch = True,labels = labs)
plt.grid()
plt.title("原石数据")
plt.subplot(1,3,2)
plt.boxplot(data_minmax1,notch = True,labels = labs)
plt.grid()
plt.title("缩放范围为0~1")
plt.subplot(1,3,3)
plt.boxplot(data_minmax2,notch = True,labels = labs)
plt.grid()
plt.title("缩放范围为1~10")
plt.subplots_adjust(wspace = 0.1)
plt.show()
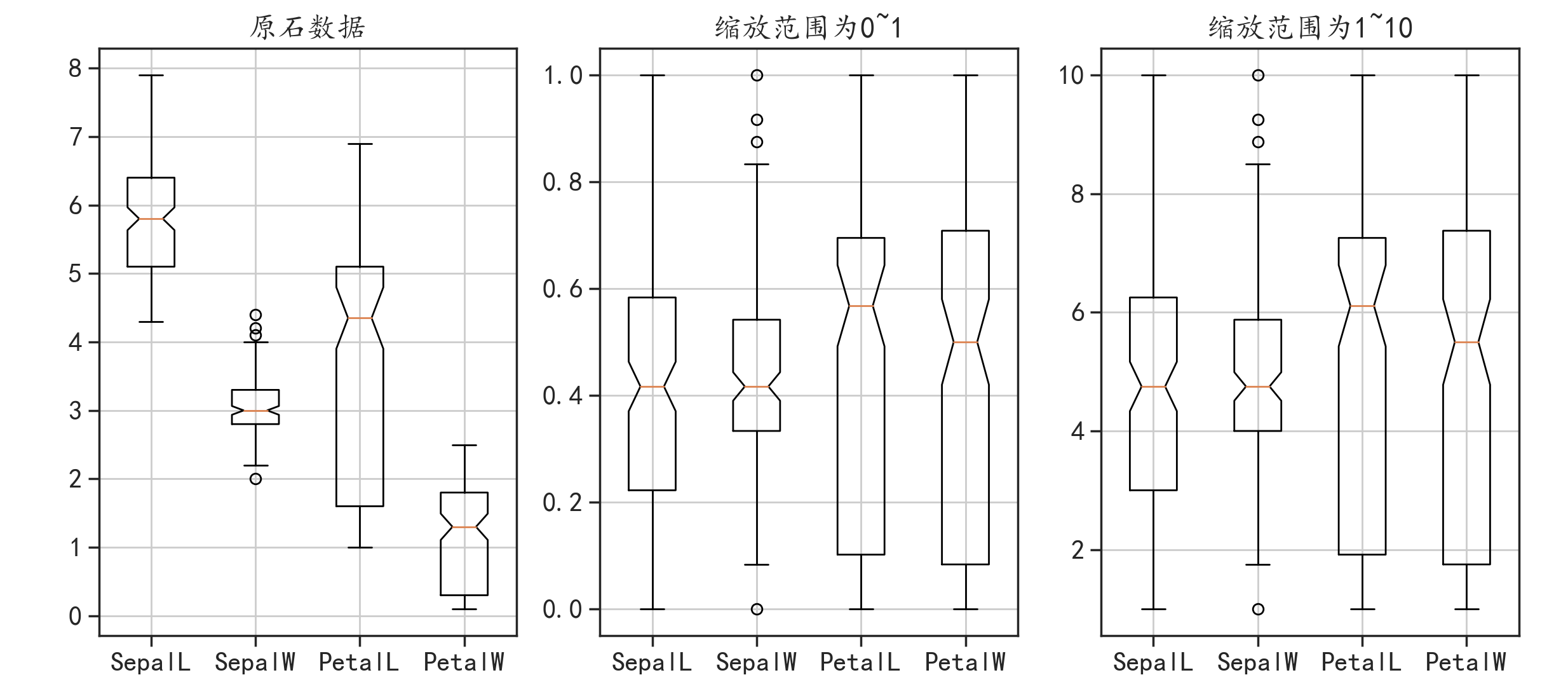
可以看到,和原始数据相比,缩放后的数据分布趋势变化不明显,但是数据的取值范围发生了改变。
preprocessing模块中MaxAbsScale()函数还可以通过最大绝对值缩放每个特征。
data_maxabs = preprocessing.MaxAbsScaler().fit_transform(data)
labs = ['SepalL','SepalW','PetalL','PetalW']
plt.figure(figsize = (16,6))
plt.subplot(1,2,1)
plt.boxplot(data.values,notch = True,labels = labs)
plt.grid()
plt.title("原始数据")
plt.subplot(1,2,2)
plt.boxplot(data_maxabs,notch = True,labels = labs)
plt.grid()
plt.title("MaxAbsScaler()")
plt.show()
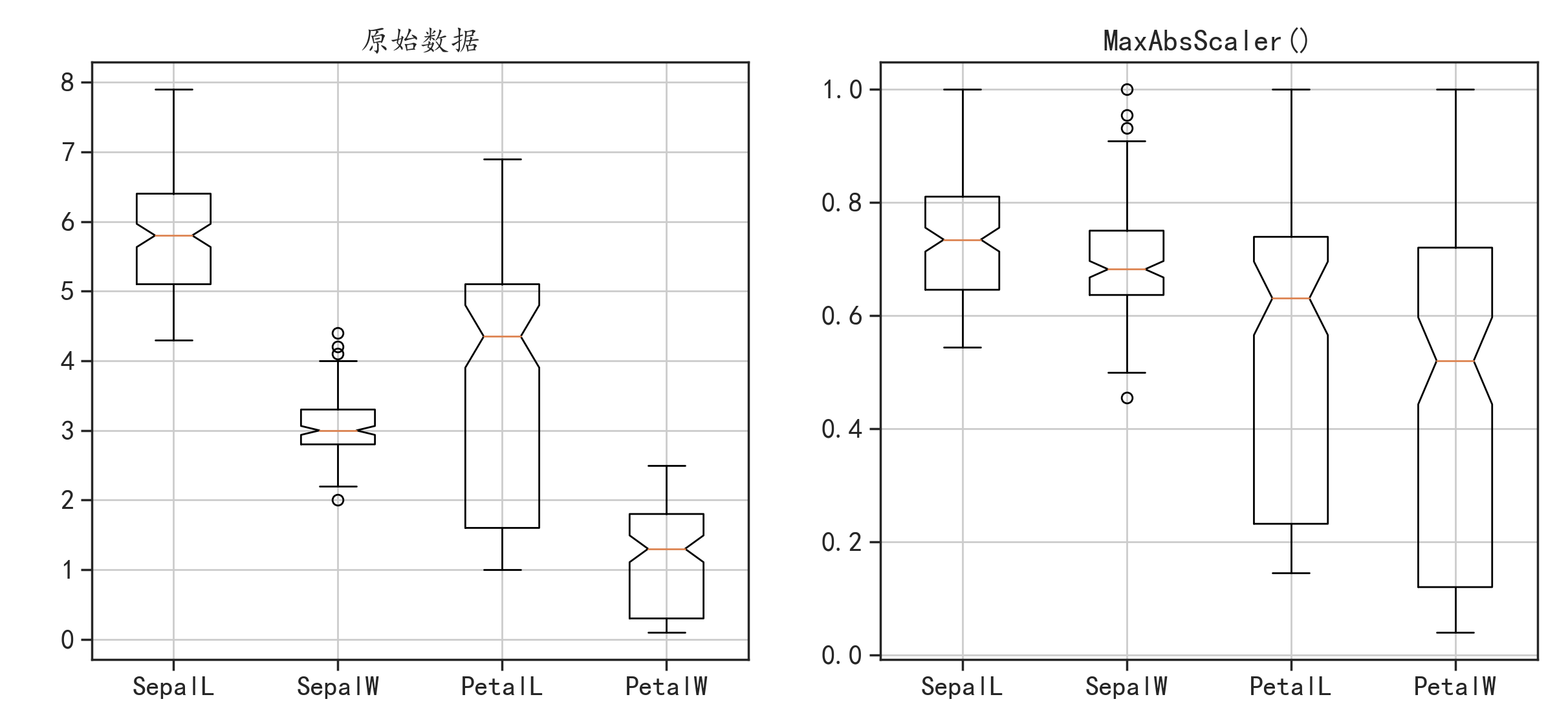
变换后数据的取值范围为0~1,但是4个特征的整体取值大小的分布和原始特征的空间分布变化较大。
🌑 数据归一化
preprocessing模块中的normalize()函数可以对数据特征进行正则化归一化。
data_normL1 = preprocessing.normalize(data,norm = "l1",axis = 0)
data_normL2 = preprocessing.normalize(data,norm = "l2",axis = 0)
labs = ['SepalL','SepalW','PetalL','PetalW']
plt.figure(figsize = (15,6))
plt.subplot(1,2,1)
plt.boxplot(data_normL1,notch = True,labels = labs)
plt.grid()
plt.title("L1约束归一化")
plt.subplot(1,2,2)
plt.boxplot(data_normL2,notch = True,labels = labs)
plt.grid()
plt.title("L2约束归一化")
plt.subplots_adjust(wspace = 0.15)
plt.show()
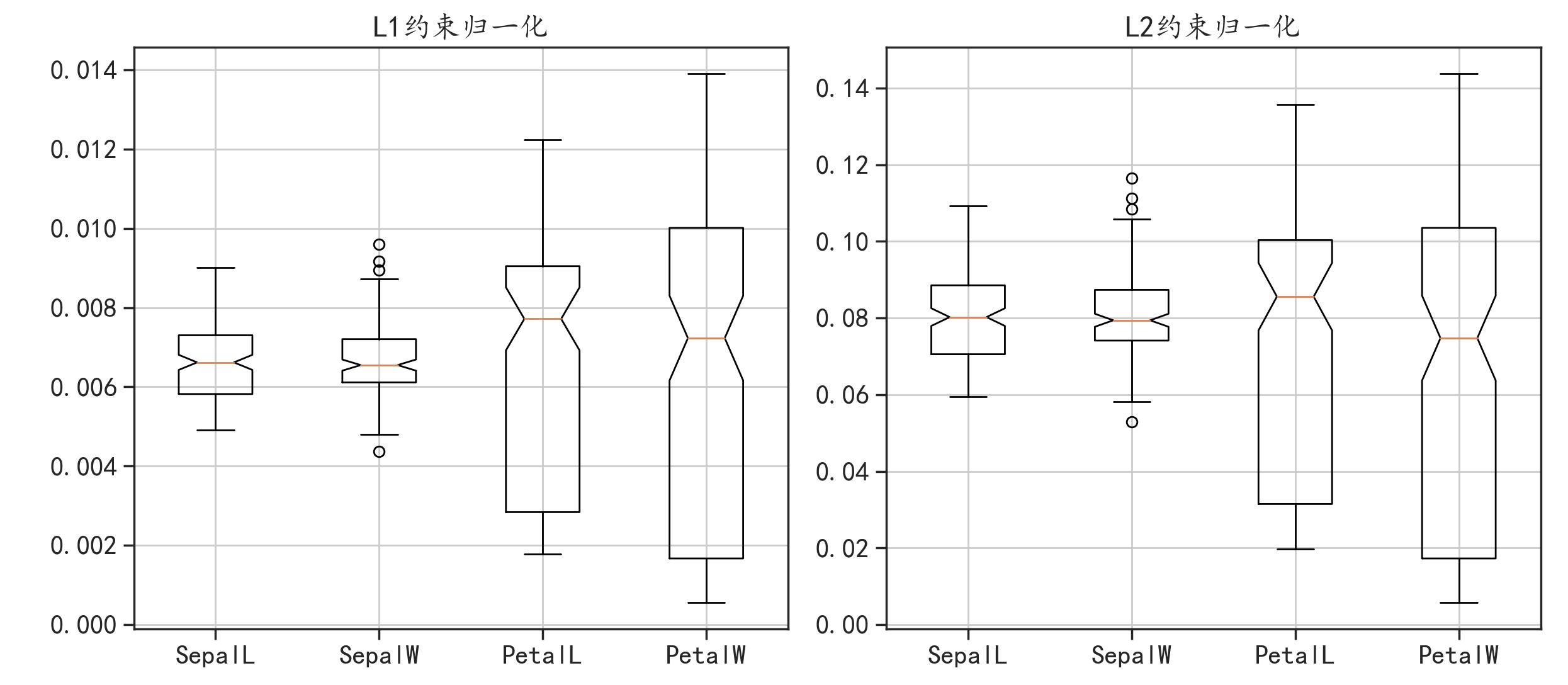
可以看到两种数据整体的取值范围相似,但是在某些特征的取值上有较明显的差异,例如前两个箱线图的取值范围较小。
下面再使axis=1来看一下可视化后的结果。
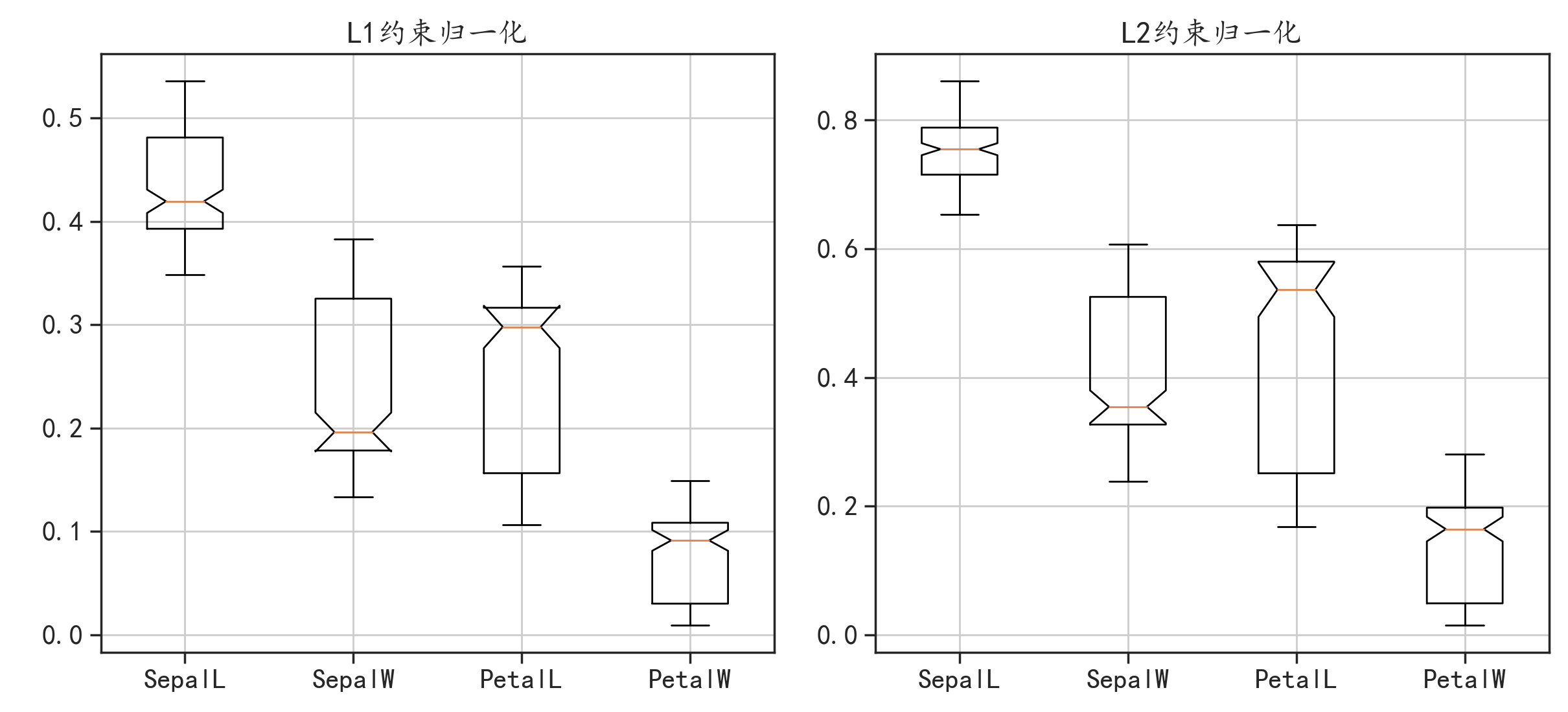
可以看到数据取值范围发生了变化,数据分布趋势变化不明显。
🌗 数据特征变换
很多时候单个变量的分布情况可能不是我们所期望的那样,而我们希望数据的分布服从正态分布,或者说接近正态分布。为此,特征变换就是用来满足人们的期望。
🌑 对数变换
下面使用泊松分布的数据使用对数变换,将其转化为接近正态分布。
泊松分布: P ( X = k ) = λ k k ! e − λ P(X=k)=\frac{\lambda^k}{k!}e^{-\lambda} P(X=k)=k!λke−λ
- np.random.possion():该函数用于生成泊松分布的数据,possion的中文意思就是泊松分布,该函数的返回值是一个数组的形状。
- np.random.rand():该函数返回一组服从0~1([0,1))均匀分布的随机样本值。
- np.log():以e为底
- np.log10():以10为底
# 导入相关的库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 中文显示问题
import matplotlib
matplotlib.rcParams['axes.unicode_minus']=False
import seaborn as sns
sns.set(font="Kaiti",style="ticks",font_scale=1.4)
np.random.seed(12)
x = 1 + np.random.poisson(lam = 1.5,size = 5000) + np.random.rand(5000)
lnx = np.log(x)
plt.figure(figsize = (10,6))
plt.subplot(1,2,1)
plt.hist(x,bins = 50)
plt.title("原始数据分布")
plt.subplot(1,2,2)
plt.hist(lnx,bins = 50)
plt.title("对数变换后数据分布")
plt.show()
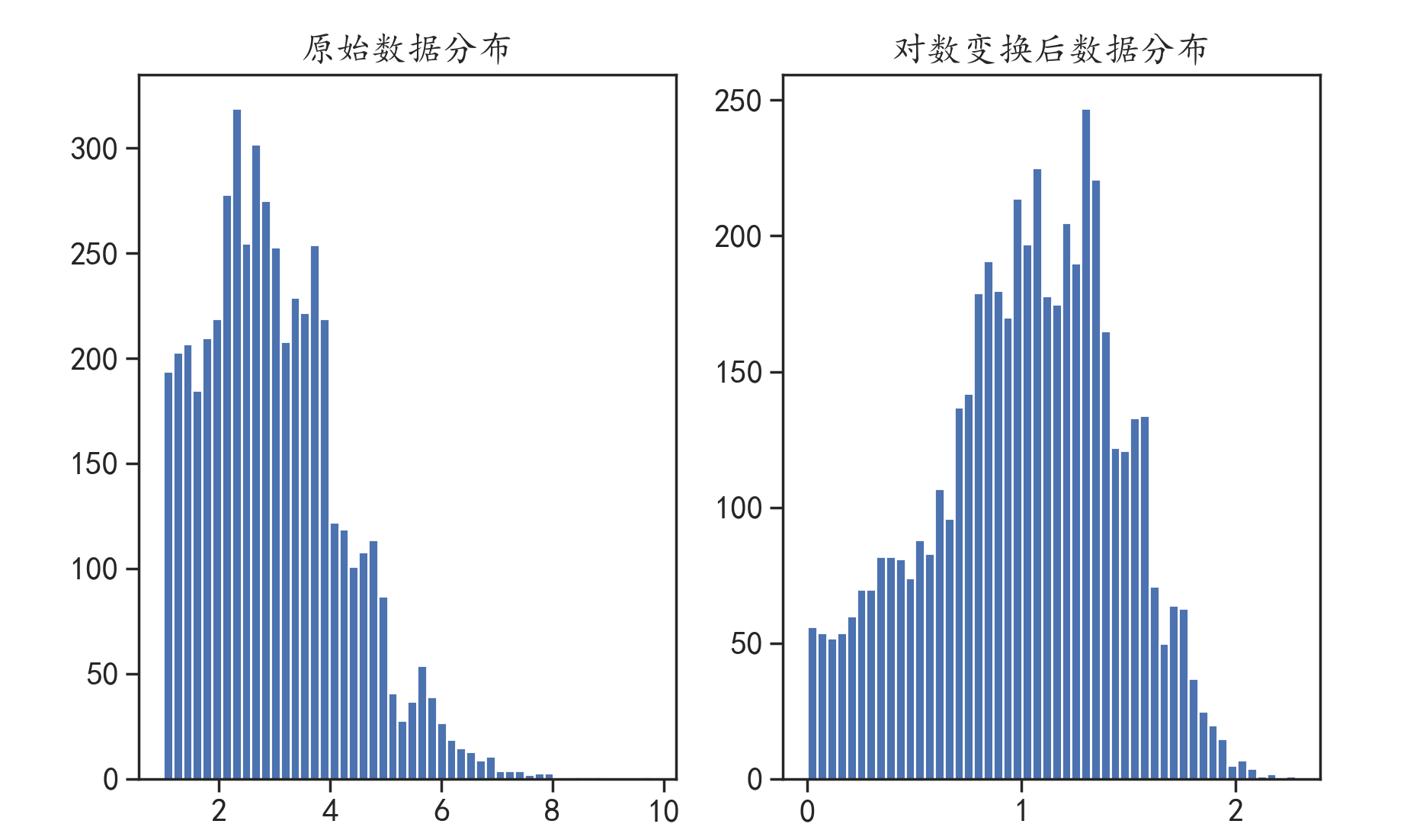
可以看到,服从泊松分布的数据经过对数变换后,其分布情况更加接近于正态分布
🌑 Box-Cox变换
该变换是一种自动寻找最佳正态分布变换函数的 方法,计算公式为:
y
(
λ
)
{
y
λ
−
1
λ
,
λ
≠
0
l
n
y
,
λ
=
0
y(\lambda)\begin{cases} \frac{y^{\lambda}-1}{\lambda},~~~~~~\lambda \ne 0\\ lny,~~~~~~~~\lambda = 0\ \end{cases}
y(λ){λyλ−1, λ=0lny, λ=0
λ
\lambda
λ在取不同的值时有不同的数据变换效果,可通过scipy.stats模块中的boxcox()函数完成。
# 导入相关的库
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import boxcox
# 中文显示问题
import matplotlib
matplotlib.rcParams['axes.unicode_minus']=False
import seaborn as sns
sns.set(font="Kaiti",style="ticks",font_scale=1.4)
np.random.seed(12)
x = 1 + np.random.poisson(lam = 1.5,size = 5000) + np.random.rand(5000)
boxcox1 = boxcox(x,lmbda = 0) # 对数变换
boxcox2 = boxcox(x,lmbda = 0.5) # x^-1的变换
boxcox3 = boxcox(x,lmbda = 2) # x^2的变换
boxcox4 = boxcox(x,lmbda = -1) # 1/x的变换
plt.figure(figsize = (14,8))
plt.subplot(2,2,1)
plt.hist(boxcox1,bins = 50)
plt.title("ln(x)")
plt.subplot(2,2,2)
plt.hist(boxcox2,bins = 50)
plt.title("x^-1")
plt.subplot(2,2,3)
plt.hist(boxcox3,bins = 50)
plt.title("x^2")
plt.subplot(2,2,4)
plt.hist(boxcox4,bins = 50)
plt.title("1/x")
plt.subplots_adjust(hspace = 0.4) # 调整子图布局,修改子图间距。hspace是调整子图间高度内边距
plt.show()
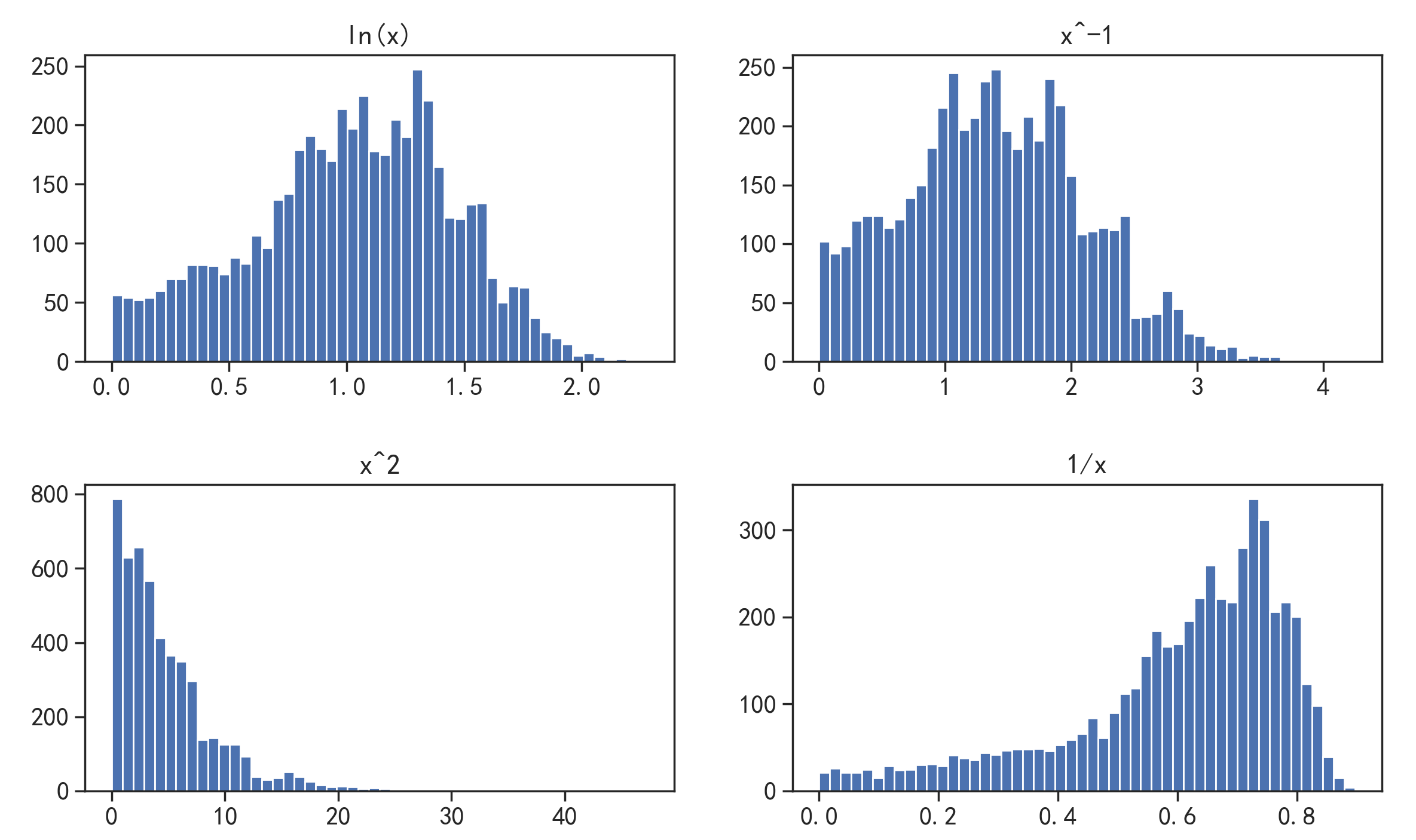
可以看到,原始数据经变换后,只有对数变换后的分布情况更接近于正态分布。
🌑 指定变换
sklearn库中的preprocessing模块提供了几种将数据变换为指定数据分布的方法,例如QuantileTransformer是一种利用数据的分位数信息进行数据特征变换的方法,可以把数据变换为指定的分布。
# 导入相关的库
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import preprocessing
# 中文显示问题
import matplotlib
matplotlib.rcParams['axes.unicode_minus']=False
import seaborn as sns
sns.set(font="Kaiti",style="ticks",font_scale=1.4)
np.random.seed(12)
x = 1 + np.random.poisson(lam = 1.5,size = 5000) + np.random.rand(5000)
QTn = preprocessing.QuantileTransformer(output_distribution = "normal",random_state = 0) # 定义将数据变换为正态分布的方法
QTnx = QTn.fit_transform(x.reshape(5000,1)) # 若要对x进行对数变换,x要转化为二维数组
plt.figure(figsize = (12,5))
plt.subplot(1,2,1)
plt.hist(x,bins = 50)
plt.title("原始数据分布")
plt.subplot(1,2,2)
plt.hist(QTnx,bins = 50)
plt.title("变换后的数据分布")
plt.show()
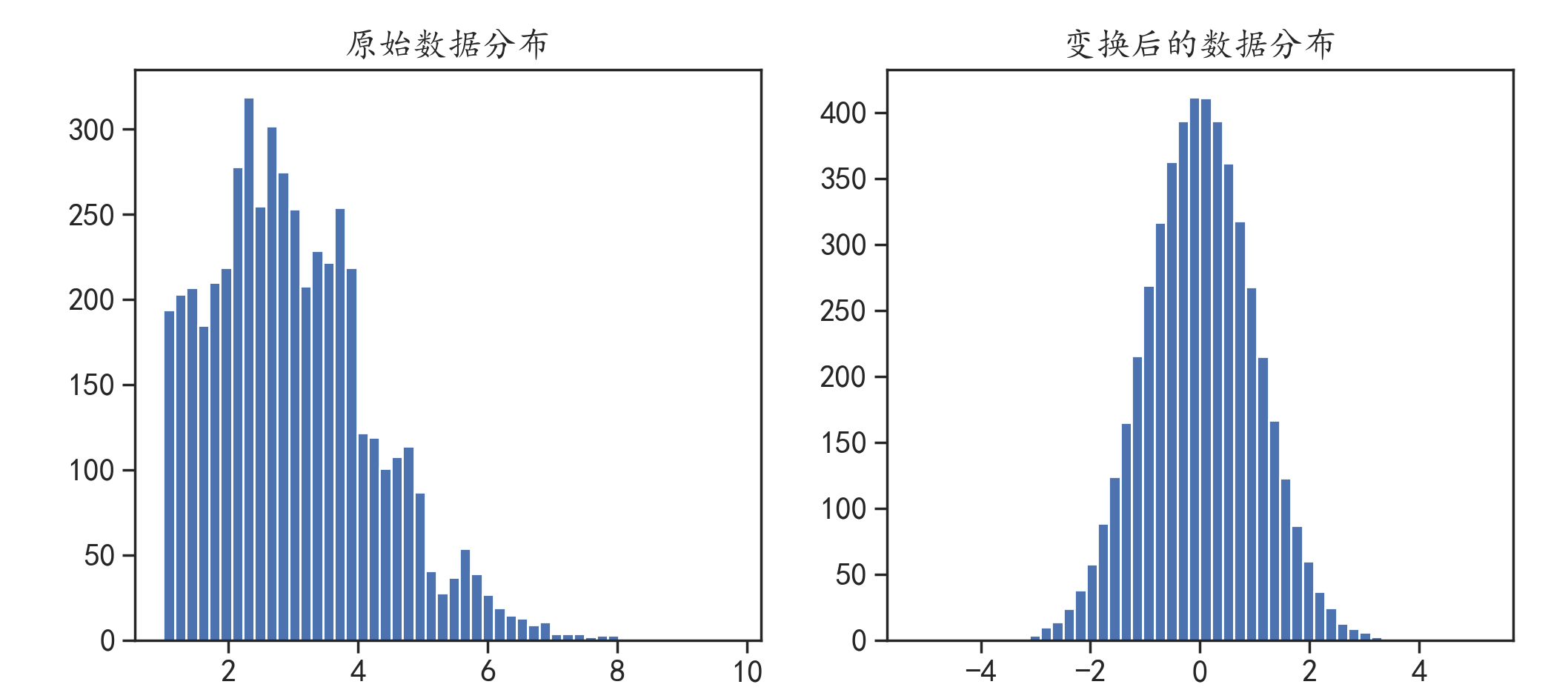
可以看到,原始数据转换成了标准的正态分布。
总结:特征变换的目的,就是为了满足建模时对数据的需求。