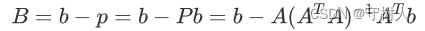标准正交向量与正交矩阵

上一节介绍过的正交向量，通过一个式子进行回顾，设q是标准正交向量组中的任意向量，则

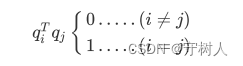
这很好地表现了标准正交向量组内各向量的性质：
不同向量之间相互垂直（正交），向量长度都为
1（标准）。标准正交向量组又被称为标准正交基，显然，相互垂直的各列一定是线性无关的。

为什么执着于标准正交向量呢？在后续就可以看到标准正交向量能够极大的简化计算，许多数值线性代数都建立在标准正交向量的基础上，因为它们容易操控，它们从不上溢或下溢。

由此引出另一个概念，标准正交矩阵。所谓标准正交矩阵Q，就是将标准正交向量组中的向量q1,q2,q3…qn列到一个矩阵中去：
Q = [q1 q2 … qn]
这样的标准正交矩阵有一个很好的性质：

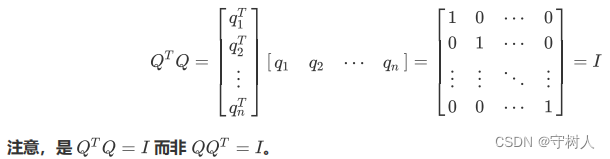
特别地，当 是方阵时，我们将这样的矩阵 称为正交矩阵。

为什么要单独将Q是方阵的情况拎出来呢？这是因为当标准正交矩阵Q 为方阵时，其必有逆矩
阵，很明显，由上面的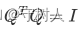
可知，Q 若为正交矩阵，其逆矩阵正是 Q，也即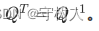
可以举一些例子：

Gram-Schmidt正交化

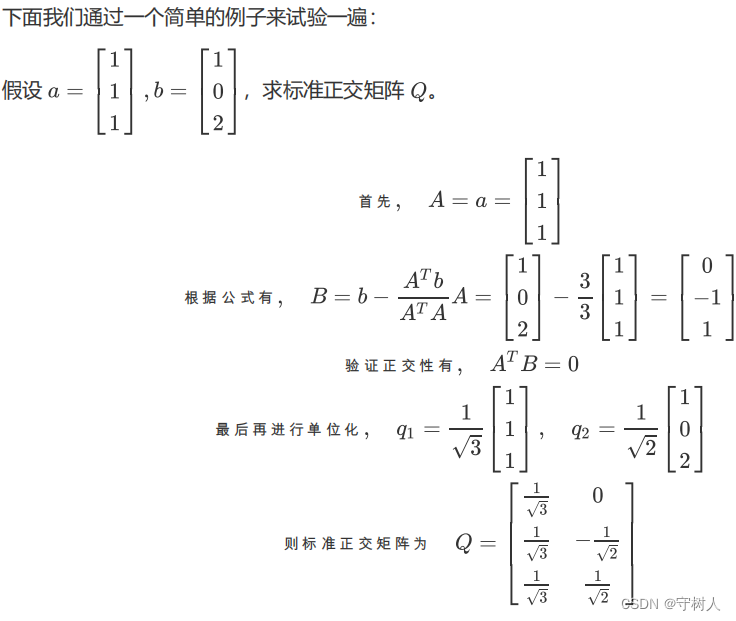
格拉姆-施密特正交化的缺点在于，由于要求的单位向量，不可避免地要除以向量的长度，而这个过程很容易产生根号，所以最终产生的标准正交向量组经常会带有根号。
Gram-Schmidt 正交化的过程如下：

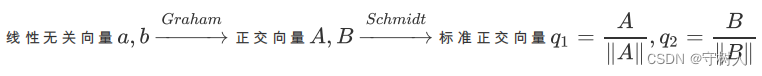
可以看到 Schmidt 也即单位化的过程是很简单的，正交化的关键在于找到 A,B。我们先从简单的情况开始，假设有两个线性无关的向量a,b：

怎样将其转换为两个相互正交的向量呢？容易联想到我们之前学习的投影，我们可以这样做：

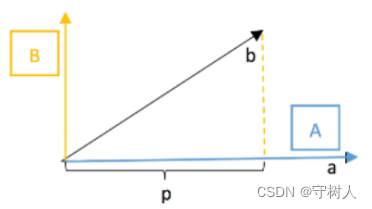
直接将a向量定位A向量，而后，我们将b向量投影到a向量上得到p，注意到，此时误差向量e = b - p恰好就垂直于A向量，故令B = b - p有：