如何理解质量

早年写过一篇未发表的论文《质量的相对性》，就是为了寻求到底什么才是质量这个问题的答案。现在，在准备了诸多超越以往的认知的概念之后，关于质量是什么的想法，也逐渐有了眉目。

质量有两种，一种叫做惯性质量，一种叫做引力质量。它俩似乎并不一样，但爱因斯坦在广义相对论中给出了两者的统一，这不用具体讨论。现在让我们只看惯性质量，把引力质量留给广义相对论。

从惯性质量来讲，一个物体有较大的质量意味着它有较大的惯性。质量的大小和惯性的大小成正比。而我们知道惯性越大，其速度越是不容易改变。速度改变的难易程度，则在于单位时间速度可以变化的程度或者说大小。而单位时间速度变化的大小，我们使用加速度这个物理量来度量。

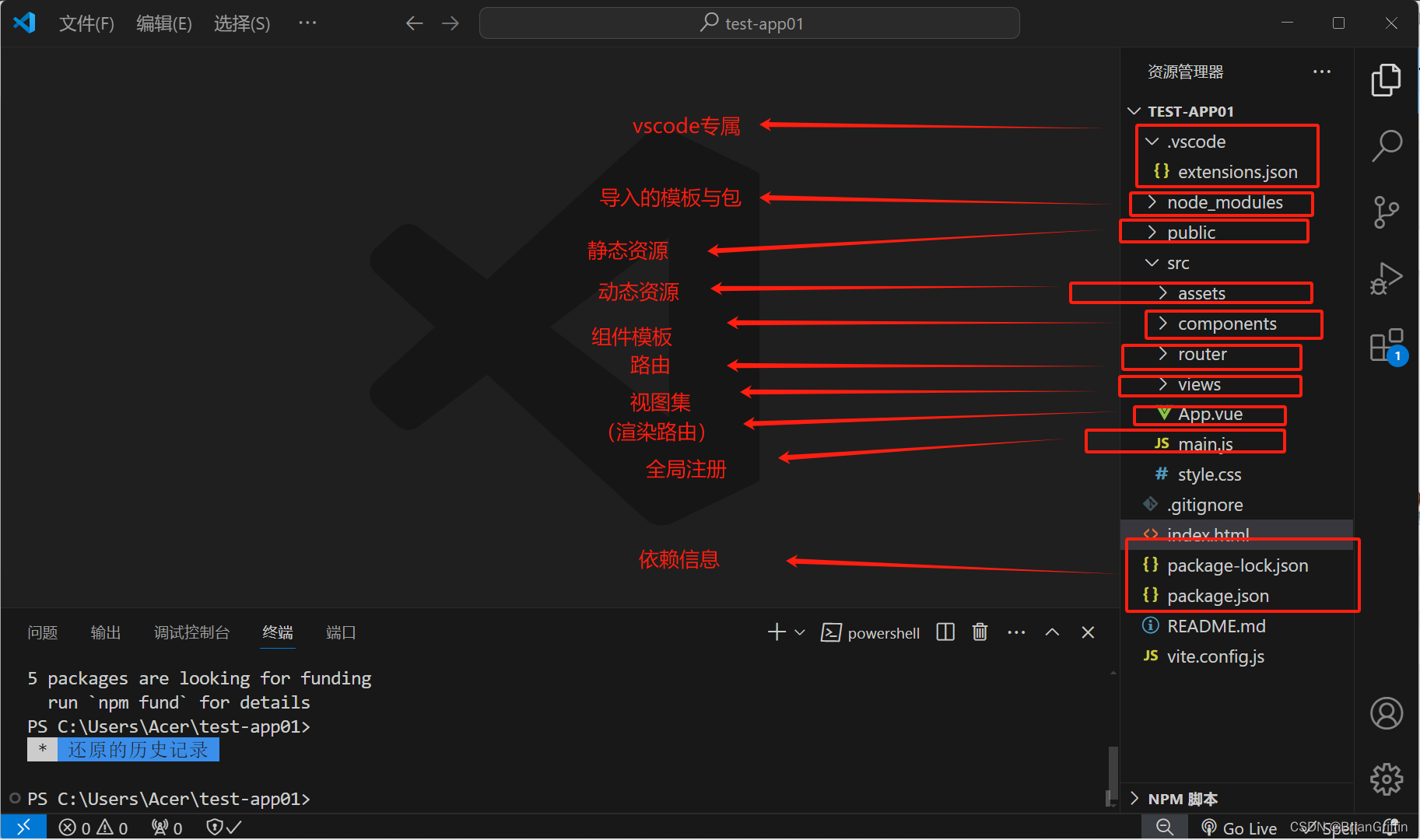
单位时间速度变化越大，对应的改变物体相对速度的难度越小；反之，单位时间速度变化得越小，则对应得改变物体相对速度的难度越大。也就是说，单位时间相对速度的改变程度，和改变物体相对速度的难度此消彼长，而这个难度是有极限的，或者说单位时间速度的改变是有极限的。比如说，单位时间为1秒的时间里面，物体运动的相对速度从0增长到光速c 就是这个极限，它可以写作，

我们用表示此消彼长中的惯性部分，则二者可以建立如下最简单的关系（奥卡姆剃刀原则），

而光速本身就可以认为是虚数单位，所以按照周期理解，则是

也就是说，这里存在

所以极限情况下也可以认为是的倒数，而此时周期为单位时间的速度变化极限，加上速度极限对应的长度变化，

所以从对应关系可见，

也就是具有加速度量纲，具有长度量纲。

而且可知，

这种形式让我们看到了事情的本质，

极限条件成立，则一般条件也成立。不难看出，牛顿第二定律中，质量和加速度的乘积，也就是力，具有纯数量纲，而纯数量纲可以导出，

这也符合我们对于长度，时间以及频率的理解。由此验证了，这里的确实就是力（负的），而也确实就是质量的最小值。那么既然力的量纲为纯数，则做功以及能量的单位就清楚了。此刻，我们故意混淆物质和光子的能量概念，以简化对能量以及普朗克常量的量纲的理解，

从和的对应关系可知的量纲为纯数；若以和的对应关系来考虑，则的量纲为，两种情况都是可以成立的。所以质量的量纲可以是，也可以是，总之它是加速度单位或者它的倒数。现在让我们考虑质能方程的变化量形式，

在认为普朗克常量为常数量纲的前提下，可以认为，

即为频率和长度的真正对应关系，也就是

以上数值并不一定正确，这是因为度量的标准和比例关系存在和现实对应的问题。但是我们可以通过该换单位制，缩放或者平移这些常数和量纲，以实现需要的数值和测量单位的改变。

现在让我们回到一个极为重要的根本问题：为什么具有运动速度为光速的光子的静止质量为0，而为什么静止质量不为0 的物体无法达到光速？

回到，

作为光速运动的光子，在单位时间里面，如果静止质量大于0，也就是说

那么单位时间中的另一项，在相同时间里面，

也就是质量的最小值大于光速，而最大加速度为静止质量的最小值，而这个值其实就是0。所以那些静止质量大于0的光子一方面不可见，另一方面静止质量仍然是0。静止质量既大于0，又等于0，这样的条件无法满足，可以导出这种光子不存在。但若不限定光子，具有这种质量和速度的物质的存在性并不受影响。

那么为什么静止质量不为0的物体无法达到光速呢？因为我们需要对其进行加速。而单位时间加速的极限就是，这时要求物体的质量为，它就只能是0（虚数单位的倒数）。但是这个情况和渐进加速并不冲突。比如在同步加速器中，被加速的电子发射出光子，就是那些单位时间累积起来速度超过了光速的电子，体现出光子的样子。

我们已经知道，质量的单位，就是加速度单位的倒数，也就是说，

此处可以认为，

或者说，存在以米计数的秒，也可以是以千克计数的秒，或者说，质量的单位千克可以认为是时间的一种表达方式，正如长度的单位米，也是时间的一种表达方式。

所以一个大质量的物体，可以认为其内部具有多个大周期的振动，或者说低频率的震动。也就是说，质量（注意，这不是长度“米”），

对于相同的振动总量n ，重复次数越多，对应的单个频率越低；单个频率越高，重复的次数就越少。所以从振动总量来说，质量指的是单个振动的重复次数。而对于频率变化来说，较低的频率也只能对应较小的频率变化，这时候单个振动的重复次数较多，质量较大，这就体现为运动状态难于改变。相反较高的频率则需要较少的重复次数，宏观物体的振动状态则易于改变。从频率的变化对应宏观物体振动状态的变化，就可以看出为什么质量大的物体惯性要大了，这是惯性质量的解释。引力质量是类似的。

一个大质量物体，我们说它质量大，一般说的是它的某些基本元素的数量众多。比如一千克的水，它具有大量的水分子。考虑单个水分子，则是考虑一个氧原子，两个氢原子的质量，我们就算是把这一千克水加速到接近光速，实质上我们也只是对单个水分子进行加速，然后把水分子加速到光速。需要的力随着水分子数量的增加而增加。而对于单个水分子来说，需要的力，只关系到其“周期”的大小。周期越大，需要的力越大。换句话说，周期大则频率低，从较低的频率上升到较高的频率，则需要较大的频率提升，它可以是小频差提升的积累。大质量的物体则有另一种可能，就是它的“分子”周期大，但分子数量少。造成的周期总量也较大。可是，这里存在单位周期大小的问题。如果一个“分子”周期很大，以至于超过了观察者的周期长度，那么它就会体现出一个不断变化的相差，进而体现为周期性的“转动”，并且因为自身的周期较大，而在周围时空创建“钟慢”引力场。

通过这些分析不难发现，有两种东西存在，一种是物质，一种是物质的质量。而质量更像是物质引发的质量场所体现的效果。比如某种物质，它激发了电磁环境中的质量场，质量场之间相互作用，就产生了万有引力的效果。比如A激发的质量场，中心周期更大，周边周期更小，B也是如此，那么A和B就有相互陷入到对方中心的倾向，进而构成了引力。我们测量的物质，都只是物质对周边电磁环境的影响，而不是物质本身。由此而言，质量变成能量才有了实际的意义。也就是说，并没有什么质量变成能量，只是能量原来的形式是某些物质激发的特定电磁场，后来这些物质离开了，特定电磁场就以另外的形式表达出来，比如说被释放了。所以质量消失，也只是能量从质量的形式变成非质量的形式而已。终究都是电磁场的表现方式。

的本质是，

就是能量子( )发生转变的倍/次重复。而这里面，

这就给出了以质量形式存在的电磁能量和常规电磁方式存在的电磁能量的对易关系。

由此可以知道，一些“子”，比如电子一类基本粒子，他们能够创造对应的场，比如电磁场或者其它可能的场。“子”可以被认为是频率极高的振动，而“场”则是它们对应的电磁控件中的振动构成，“子”和“场”之间很可能具有振动总量相同的对应性。它们共同复合而成为这个物质世界。

狭义相对论中，洛伦兹变换给出了洛伦兹因子，

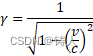
可见质量也是随着相对速度变化而变化的。我们知道整个狭义相对论都是基于光速不变的基本假设，而光速的不变的数值则来自于真空中磁导率和介电常数的乘积的平方根，所以实际上狭义相对论描述的从头到尾都是电磁学规律。那么由此来说，这里的质量也只能是在电磁前提下定义的质量。虽然我们已经证明洛伦兹因子中的

只是互相观察造成的错觉，由此得到的洛伦兹因子γ 并不真的成立，但是质量之间出现和长度之间一样的比例关系仍然是正确的，也就是说，

由绝对速度的比率导出质量之间的比率，就自然超越了洛伦兹因子γ 引入的光速上限问题。现在，让我们再次回顾洛伦兹变换，以说明为什么洛伦兹因子γ 引入光速上限的问题并不是真问题。

引用《再论洛伦兹变换》开头的一段文字，

考虑一列火车（称为惯性系S' ），以相对于站在0点的观察者（称为惯性系S ）相对速度为v ，自左至右驶过0点，此时在火车上从左至右发射一个光子，经过一段时间之后，光子到达位置x ，而这个位置，则是火车所在惯性系的对应位置x' 。光子从0点出发，到达位置x ，和到达位置x' 是同一件事。而得到x 和x' ，两个（显然）不同的结果，（显然）是因为在两个不同的惯性系中分别观察而得到的。由此列出方程组如下，

不难发现，若仅考虑宏观低速的情况，则可以按照伽利略变换中任意时空的时间流逝的速度都相等，则可以得到，

代入方程

x=x'+vt

x'=x-vt

这两个方程其实是同一个方程的两种写法（移项并交换两端即可看出）

从上述方程组导出洛伦兹变换，只需各自在方程右侧加上一个比例系数k ，为区分伽利略变换，我们要求，

这就是问题出现的地方：这里要求，但是“物理定律在不同的惯性系中应当保持相同的形式”这一要求必须满足，剩下的就只有一种可能性，

符合这一条件的就只能是虚数单位的比值，因为虚数单位的比值，可以等于它自己的倒数，

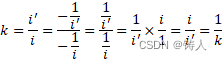
后来我们意识到这里的虚数单位，其实就是惯性系的绝对速度，或者说惯性系自己的光速，

而这个光速在观察者时间单位不变的前提下（也必然如此），就是单位长度的比值，或者说，频率变化量的比值，

k=∆f'∆f

而频率变化量，对于每个惯性系来说，又是时间变化量的对应物，而这个时间变化量就是周期本身，所以对应关系为，

由此来说，比例常数k 还可以写成，

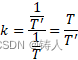
然而我们又知道，

于是比例常数又可以写成，

此处似乎什么都没有做，只是对于一个概念的由来进行了一次验证。但也充分说明了比例常数自己可以颠倒的原因。事实上，我们可以认为构成长度单位的，既可以是频差也可以是周期，而两者可以认为是互为负倒数的，这是因为两者正好就对应于虚数单位和它的倒数。所以，长度的本质，就是它即是周期的重复，也是频差的重复，也就是说，周期和频差，也就是对时间（或者频率）的两种不同理解，共同定义了长度这个物理量。由此回到，

我们就不用再执着于两个方程的必须相等，而是允许它们不相等，而当它们不相等可以被接受，就不必纠缠出

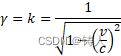
这样的隐含了光速上限的结果。尤其是可以认为两个k 互为倒数（且不需要相等），那么，我们就可以写出，

进而导出，

这就得出了

当然，它就是，

因为做相对的匀速直线运动的两个惯性系都从时间为0开始，经历了相同数量的周期，所以这个比值当然也是时间的比值，当然也是频率提升的比值。

所以“物理规律在不同惯性系应当表现出相同的形式”，这句话没有错，但是将它理解为

则是宏观上的看法。因为只有在虚数单位前提下，才能成立，而虚数单位意味着极大或者极小的数值。而这正是微观和宏观之间的长度和时间的比例关系造成的幻觉。这种幻觉导致这种比例关系的数量和它的倒数看上去是一样的（比如“一千万零一”比上“一千万”，和“一千万”比上“一千万零一”，两个比值几乎都等于1，但是大小略微不同）。正确的理解是，确实“物理规律在不同的惯性系表现出相同的形式，但不意味着比例关系由此而发生逆转”。大的还是大的小的还是小的，虽然两者都很大，或者都很小，使得两者看上去几乎是一摸一样的，比值也几乎就是1，但是它们的比值确实不为1，则是它们的现实。

排除了这个由宏观经验引入的错误，就对惯性系和光速上限实现了解耦，后面的部分就是你所熟悉的了。

有了上述讨论，似乎很多问题豁然开朗了，但是也引入了新的问题，就是我们认为的长度，究竟是应该用频差单位来度量，还是以周期来度量？光速这种东西，在单位时间也就是某种基准物（可能就是电子）的周期上经历的长度，到底是频差，还是时差（也就是周期）？如果是频差，那么米的定义就是赫兹的平方，如果是时差，它的单位就是纯数量1。

让我们考虑时间间隔从大到小的变化过程，这里的时间间隔自然就是某种周期，若非如此，我们也不会想到用它。时间间隔比较大的时候，我们可以用更小的周期来度量，比如某个基准周期（电子的周期），基准周期重复的次数，它是一个纯数，就是这个周期的“长度”，单位则是基准周期的大小。随着被度量数量的越来越小，最终一定会遇到基准周期的大小，以及小于基准周期的大小，这时候我们就会遇到半个基准长度的问题，但是如果这时候我们用频率来度量，则会得到频率数值可以被重复两次。

所以由此可以知道，我们先定了一个基准周期或者基准频率，度量宏观长度的时候，我们把它当作基准周期，并记录基准周期重复的次数；度量小于这个基准周期的微观长度的时候，我们就用对应的基准频率来度量基准频率重复的次数。频率和周期互为倒数，两者的翻转从时间这个基本概念上共同导出了长度的概念（这样定义长度，就自动解决了伽利略变换无法在微观高速条件下成立，而洛伦兹变换却可以的疑虑。因为洛伦兹变换把时间或者周期的比率（用于宏观）和频率差（用于宏观）的比率的两种比率的差别屏蔽掉了。使得在微观高速条件下也能借用伽利略变换的方法。但其失误也在于此，它混淆了宏观“物理定律在不同惯性系中具有相同的形式”和“惯性系之间本质上的差异是数值而不是形式”这两种不同的视角产生的效果）。

所以不难看出，光速就是这个基准周期或者频率差和单位时间的比率。我们显然是假定了这个数值处处都一样的。但正如我们不可能真正细察每一个惯性系，所以惯性系的基准很可能是每一个都不一样的。这种每一个都一样，也只是我们对于大数都差不多大的一种粗略的理解，正如先前提到的“一千万零一”比上“一千万”，和“一千万”比上“一千万零一”，抑或是299796458和299796457以及299796459都差不多，一样，都是我们对于巨大数量都应该一样的一种误解。

有了长度的两种定义，现在让我们再次回答关于光子到底用多长时间才能走完1光年的问题。因为我们不能把光子当成存在静止质量的普通物质，所以我们也不能用γ 或者k 去计算，所以光子走1光年到底需要多长时间，无法用这种方式回答。

但是我们知道，能够产生特定频率的光子的方法，比如用同步加速器产生光子。产生光子的电子在它发射光子的时候一定有自己的波长和频率，那个频率就是光子频率的基准参考，或者说那个波长就是光子波长的基准参考。在那个基准参考基础上，才定义了两点的长度。当然那两点的长度恐怕是这个单位的极大数量(频率数值)的整数倍数。

由此我们知道，对于不同频率的光子来说，两点的距离是不同的，要完成这个距离，需要的时间也是不同的，可以认为光子频率越高，宏观距离所需要的时间单位就越小，两点之间就显得越短。所以对于光子来说，到底要多久才能走完一光年，是决定于它自己的。换句话说，那个距离是不是一光年也是它自己决定的。而这个数值，虽然可以很短，但通常不太可能是0，除非那个光子具有极限频率。

所以我们经常说，在伽马射线频段观察了距离地球若干光年之外发生的事件，是在若干光年之前发生的，这种说法并不正确，因为对于高频光子来说，那若干光年的距离，恐怕只在咫尺，到达地球需要的时间也只在顷刻。对于它来说，那个距离从来就没有那么远，也根本不用那么多的时间。所以也不会发生什么不同方向上的遥远的时空中同时发生了一系列事件，就像约好了一样，一起到达地球。根本就不是这回事。这是我们对于时空本质的理解错误造成的错误认识。

回到关于质量的讨论，既然长度的单位米，在单位长度之外可以被认为是秒，而在单位长度之内则可以认为是赫兹，也就是说，长度单位是时间和频率在不同范围的表象的统一；那么，我们也可以把这个观念带入到质量上来，

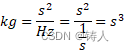
也就是

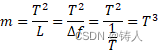
前者在于描述宏观物体在时空中体现出的惯性，而后者描述的是微观频率的效果，比如说

这时候我们看的不是质量，而是它的倒数。正如很多时候我们看的不是电路中的电阻，而是它的倒数（电导）一样，从频差的角度讲，它是一个巨大的数值。

而这么大的一个频差，能产生何种作用呢？首先，这个频差产生了“负的惯性”，

大量积累频差会在大量的质量周围产生一个很大的-T ，它会减小身在其中的其它质量的惯性，或者说周期。使得其它质量更容易向着更小的周期方向移动，这个效果，就是引力。引力对距离引力中心更近的质量减小周期长度更多，反言之，也可以认为距离引力中心更近的地方引力场本身的周期更长。这是一个A比B大，可以认为是B比A小的同义反复。由此推断，惯性质量指的是质点受到空间影响导致的惯性的度量，而引力质量则表达了质点受到其它质点造成的空间影响导致的周期梯度。

有了上述对质量的理解，我们可以正式的进入下一个问题：物质到底是什么。

光子是没有静止质量的，它可以以光速运动，而其它不能达到光速的，或者说非常难于达到光速的，物质有静止质量。我们把质量看成相对速度或者绝对速度在单位时间里面改变的难易程度的负对应物，那么光子显然其绝对速度的不可改变或者说其改变不可察觉，都使得它和静止质量无关。

首先得明确的是，质量不是物质，质量是物质的一种属性，就像是长宽高都是物体的属性，不是物体本身。光速是光子的属性，但不是光子本身，另外其它什么东西是否也可以具有这种属性，也不是由光子这个前提限定的。

惯性是物质的属性，或者说，是物质存在所体现出来的性质，这性质在试图改变其运动状态的时候才体现出来，我们用质量这个数值来衡量惯性的大小。所以本质上来说，质量是一个独立变量，物质本身是另一个独立变量，并不能假定物质到底和质量有什么关系。比如电性，最外层只有一个电子的元素有一整族，这些元素的离子都是一价的，元素和价电子的个数是彼此独立的。

从这个角度来看，其实也可以存在某些物质具有一样的质量，但是却是不同的物质。我们看待质量，总是看某个基准质量的重复次数，比如单个质子或者中子的质量的若干倍，但并不能认为，那个单个质子或者单个中子，真的就是一样的。因为毕竟我们看到的是它的属性，正如一价粒子不一定有多少个电子，而只是最外层有一个电子。

所以说物质，哪怕是最基本的电子，也可能有着不同的“内核”，虽然它们都带一个基本电荷的负电。哪怕是最基本的中子和质子，也可能具有不同的“内核”，虽然它们都带一个核子质量的单位。

既然质量这个属性和物质本身的实在，至少是两个独立变量，那么我们就可以认为，存在一个质量场，在这个质量场里面，物质本身对其做出了改变或者影响，进而使得这个场的局部体现出这种物质对应的质量属性。也就是说，质量属于质量场，而不属于物质本身，但受到物质本身的影响。这样的话，各个物质实体就可以通过质量场来进行交互作用，实现惯性或者引力的效果了。

目前，我们区分不出物质实体和它的质量场影响，但是，从其惯性角度来看，

它是一种对于位移改变的对抗，而且它还有

可见微小周期的立方更为微小，而对应的频率极大，它作为虚数单位，又对应周期改变的阻抗，所以我们可以这样认为：那个3次周期所指的就是这个物质的实体，而负的周期，则是它在质量场中的体现。这两个东西，“相等”，是因为我们无法将其区分开来。

无法区分，其实就是守恒律。比如说，我们知道某处有电子，然而其当下生灭的本质，就注定了它是不稳定的，那么我们如何认为它是稳定的？是我们自己期待了它的稳定，尽可能的期待并验证了它的稳定，直到它不在稳定的出现在那附近为止。这个“电荷守恒”，并不是那个电子能够恒常存在，只是我们对它恒常存在的期待。可以认为，从当下生灭的角度来看，它早就不是它了。那么如果我们认不清某种高频的振动和它的低频的对应物，我们就会认为那就是它，或者说一个高频和一个低频组合起来的，就是它。至于什么时候是高频的什么时候是低频的，我们真的分不清。

所以就有了，