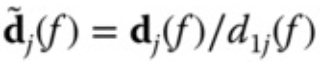题目来源:最大子矩阵 - 蓝桥云课 (lanqiao.cn)
问题描述
小明有一个大小为 N×M 的矩阵, 可以理解为一个 N 行 M 列的二维数组。
我们定义一个矩阵 m 的稳定度 f(m) 为f(m)=max(m)−min(m), 其中 max(m) 表示矩阵 m 中的最大值, min(m) 表示矩阵 m 中的最小值。
现在小明想要从这个矩阵中找到一个稳定度不大于 limit 的子矩阵, 同时他还希望这个子矩阵的面积越大越好 (面积可以理解为矩阵中元素个数)。
子矩阵定义如下: 从原矩阵中选择一组连续的行和一组连续的列, 这些行列交点上的元素组成的矩阵即为一个子矩阵。
输入格式
第一行输入两个整数 N,M, 表示矩阵的大小。
接下来 N 行, 侮行输入 M 个整数,表示这个矩阵。
最后一行输入一个整数 limit, 表示限制。
辎出格式
输出一个整数. 分别表示小明选择的子矩阵的最大面积。
样例输入
3 4 2 0 7 9 0 6 9 7 8 4 6 4 8样例输出
6样例说明
满足稳定度不大于 8 的且面积最大的子矩阵总共有三个, 他们的面积都是 6 (粗体表示子矩阵元素)
2 0 7 9
0 6 9 7
8 4 6 4
2 0 7 9
0 6 9 7
8 4 6 4
2 0 7 9
0 6 9 7
8 4 6 4
评测用例规模与约定
对于所有评测用例, 0≤0≤ 矩阵元素值, limit ≤105≤105 。
题目大意
给定一个N*M的二维矩阵和一个数字limlit,求出符合稳定度f(m)<=limit的面积最大的子矩阵。
f(m)为当前子矩阵的最大值-最小值
解法一:暴力法(通过30%)
通过四重循环(四条边)枚举每个子矩阵,然后再计算当前子矩阵的最大值和最小值之差,若差值满足<=limit,则维护更新面积最大值。
算法复杂度大于O(n^4)
解法二: 尺取法+单调队列(通过100%)
解题关键(三问):
1、如何较为快速地确定当前子矩阵的大小?
双指针算法(尺取法)
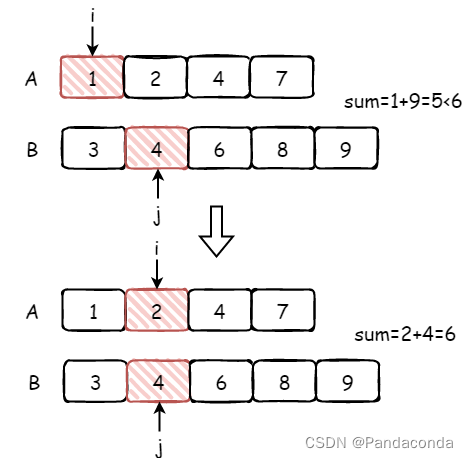
【图解】尺取法
1、一开始左右指针都是从左端点开始

2、右指针先向右移动
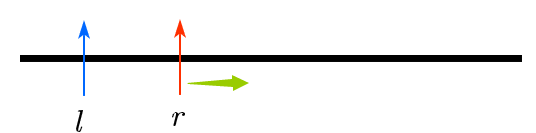
3、右指针移动到刚好满足f(m)<=limit 的临界位置

4、右指针再向右移动,这时候在区间[l, r']就不满足 f(m)<=limit
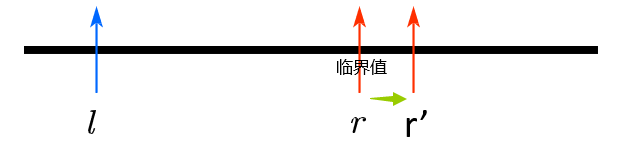
5、此时开始移动左指针
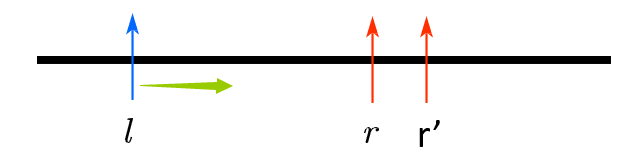
6、当左指针移动到刚好满足f(m)<=limit 的临界位置时,右指针开始移动,这样周而复始,直到右指针达到终点。

观察数据,可发现行的数据范围较小,列的数据范围较大,因此子矩阵的上下边可以通二.重遍历确定,复杂度,子矩阵的左右边采用双指针算法进行确定,复杂度
。
算法复杂度
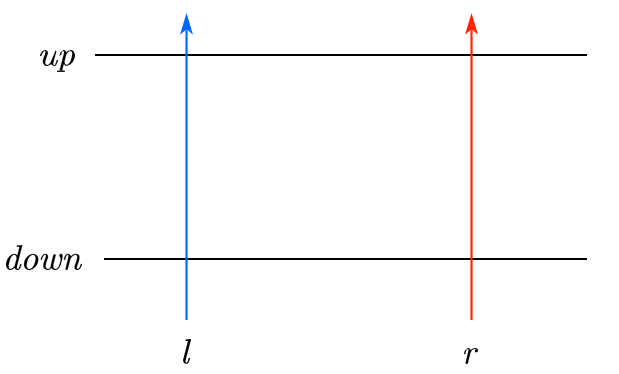
2、如何较为快速地找出当前子矩阵的两个最值?
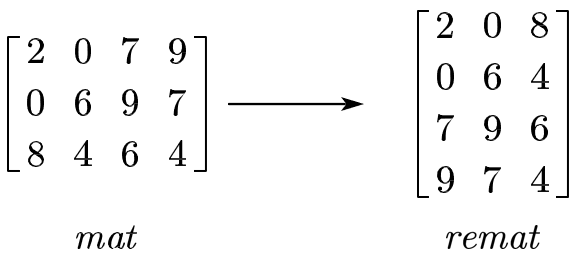
每次移动左右指针,都会后一整列的数字进入或退出当前子矩阵,我们需要先计算出当前列[up,down]范围的最值。优化:通过转置矩阵,我们可以利用切片的方式,不用循环求出原矩阵每一列[up,down]范围内的最值
3、当前子矩阵实在不断移动的,如何在移动过程中维护最值?
使用两个队列分别记录当前子矩阵的最大值和最小值,维护队列的单调性,双指针移动过程中时刻更新队列。
单调队列
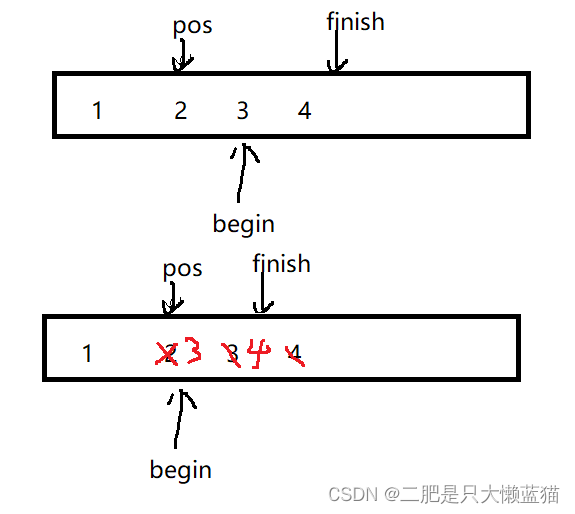
维护最大值的单调队列示例:
第一个数字直接加入队列,后面每一列如果出现的数字比队列最后一个元素小,则加入队列,否则去掉队列最后一个元素, 再与队列最后一个比较,直到队列为空或者该数字比队列最后一个元素小再将该数字加入队列。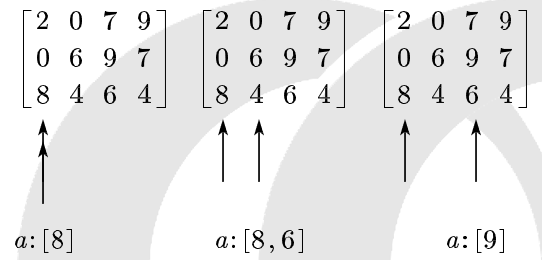
维护最大值的单调队列,内部元素是递减排列的
维护最小值的单调队列,内部元素是递增排列的
解题思路:双指针+单调队列
1、二重循环对矩阵的上下边界进行遍历
2、对于每个确定的上下边界up,down,左右边界采用双指针算法确定
3、使用两个队列分别记录当前子矩阵的最大值和最小值,维护队列的单调性,双指针移动过程中时刻更新队列
4、初始res=0保存结果,双指针移动过程中维护最大值
代码演示
from collections import deque
n, m = map(int, input().split())
mat = [list(map(int, input().split())) for _ in range(n)] # 二维列表存矩阵:n行m列
lim = int(input())
max_res = 0
# 转置矩阵 m行n列
remat = [[0] * n for _ in range(m)]
for i in range(m):
for j in range(n):
remat[i][j] = mat[j][i]
for up in range(n): # 两个for循环遍历上下边
for down in range(up, n):
l = 0 # 左指针初始化
maxq = deque() # 最大值的单调队列
minq = deque() # 最小值的单调队列
#maxq.append(max(remat[l][up: down + 1]))
#minq.append(min(remat[l][up: down + 1]))
for r in range(0, m):
newmax = max(remat[r][up: down + 1]) # 右边新的一列l:[up,down]最大值
while len(maxq) and maxq[-1] < newmax:# 最大值的单调队列的最后一个比新的最大值小
maxq.pop() # 删除队列最后一个
maxq.append(newmax) # 把新的一列的最大值放入队列
newmin = min(remat[r][up: down + 1])
while len(minq) and minq[-1] > newmin:
minq.pop()
minq.append(newmin)
cumax, cumin = maxq[0], minq[0] # 子矩阵的最大值和最小值
while cumax - cumin > lim and l < r: # 最大-最小>lim,左指针<右指针
if len(maxq) and max(remat[l][up: down + 1]) == maxq[0]: # 最左边的一列的最大值是子矩阵的最大值
maxq.popleft() # 删除最大值,因为左指针要向右移动
if len(minq) and min(remat[l][up: down + 1]) == minq[0]:
minq.popleft()
cumax, cumin = maxq[0], minq[0] # 更新子矩阵的最大值和最小值
l += 1 # 左指针要向右移动
if cumax - cumin > lim: # 特判:如果l=r且最大-最小>lim
continue
cu_square = (r - l + 1) * (down - up + 1) # 计算面积
max_res = max(max_res, cu_square)
print(max_res)


![[WUSTCTF2020]颜值成绩查询(布尔注入)](https://img-blog.csdnimg.cn/f3db04f98a9f4fdebdf0c3d8e7cd800f.png)