二叉树的遍历

二叉树的遍历是将二叉树的每个结点访问且访问一次

遍历按根来说常用三种

设访问根结点记作V，遍历根的左子树记作L，遍历根的右子树记作R；

有：先序遍历VLR，中序遍历LVR，后序遍历LRV。

这个遍历是递归遍历的，例如中序遍历，先中序遍历左子树，访问根，最后中序遍历右子树。叶子结点也是一个二叉树，只不过它的左右子树为空，所以每一个结点都有且仅有一次输出。

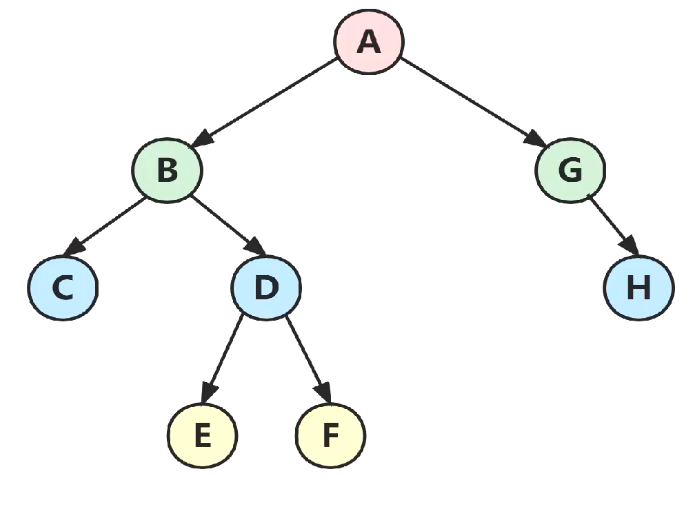
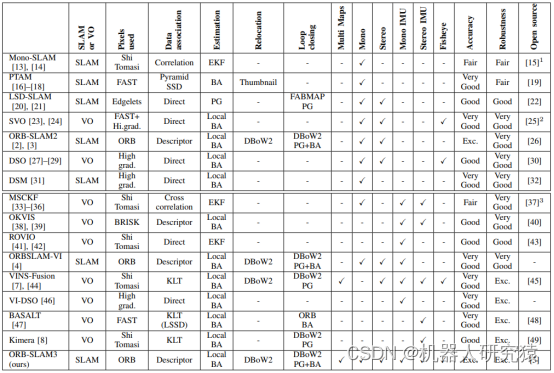
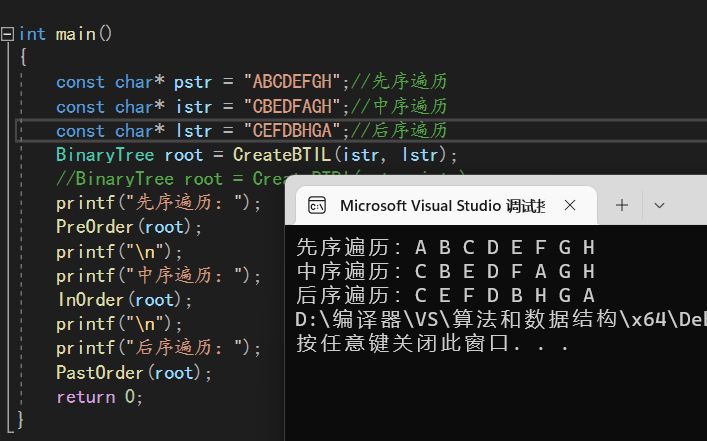
先序遍历：A B C D E F G H

中序遍历：C B E D F A G H

后序遍历：C E F D B H G A

递归遍历

链式结构

先序

void PreOrder(BTNode* p)
{
    if (p != NULL)
    {
        printf("%c ", p->data);//根
        PreOrder(p->lchild);//左子树
        PreOrder(p->rchild);//右子树
    }
}

中序

void InOrder(BTNode* p)
{
    if (p != NULL)
    {
        InOrder(p->lchild);//先遍历左子树
        printf("%c ", p->data);//根
        InOrder(p->rchild);//右子树
    }
}

后序

void PastOrder(BTNode* p)
{
    if (p != NULL)
    {
        
        PastOrder(p->lchild);//左子树
        PastOrder(p->rchild);//右子树
        printf("%c ", p->data);//根
    }
}

顺序结构

中序

void InOrder_Ar(const int* nums, int i, int n)//i是根节点下标，n是规模
{
    if (i<n&&nums[i]!=-1)//不是空树
    {
        InOrder_Ar(nums, i* 2 + 1, n);//左子树
        printf("%d ", nums[i]);
        InOrder_Ar(nums, i * 2 + 2, n);//右子树
    }
    printf("%d ", nums[n]);
}

先序和后序将输出if里面的顺序改一下就好。

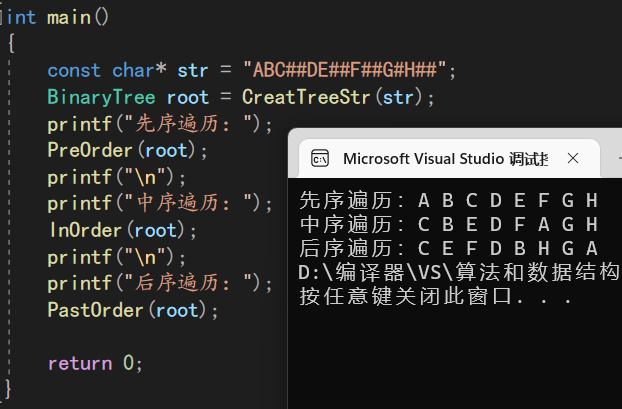
创建二叉树

使用数组创建二叉树

创建二叉树时需要直到其亲子联系，所以用先序遍历创建二叉树是最简便的

首先结点类型是一个结构体，包含左、右孩子的指针，和当前结点的值

typedef char ElemType;
typedef struct BTNode//BinaryTreeNode二叉树的结点类型
{
    BTNode* lchild;
    BTNode* rchild;
    ElemType data;//当前结点的数据
}BTNode,*BinaryTree;

然后，用字符串建立树，如果为空则输入#，不为空则申请空间，给结点赋值，并继续创建它的左、右子树。

这个传参时一定要用引用，不然左子树创建完接着不是创建当前结点的右子树,而是之前左子树的子树（重复使用前面的字符串了）；使用引用后，用到的字符串不会重复

BTNode* CreatTreeStr(const char* &str)
{
    if (str == NULL || strlen(str) <= 0)return NULL;
    BTNode* s = NULL;
    if (*str != '#')
    {
        s = new(BTNode);
        if (s == NULL)exit(1);
        s->data = *str;//根
        s->lchild = CreatTreeStr(++str);//左
        s->rchild = CreatTreeStr(++str);//右
    }
    return s;
}

已知先序序列和中序序列，创建二叉树

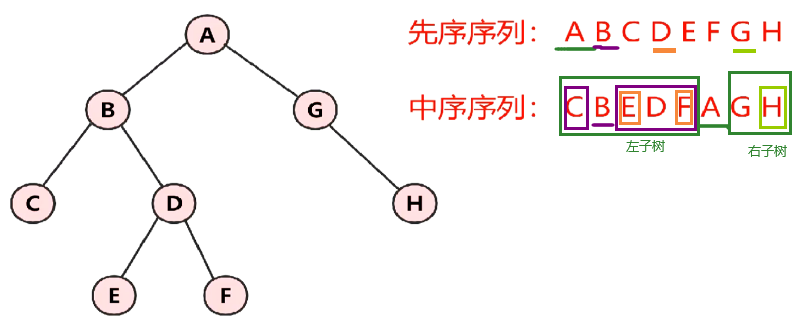
先序遍历顺序找根，中序遍历分左右子树

初始时先序遍历第一个元素是根，给根赋值，然后在中序序列中找根的位置pos，分别创建左右子树；左子树范围为从先序遍历的头的下一个元素往后数pos个；右子树的范围为剩下的；传参数时，先序序列和中序序列的范围都需要改变；

创建二叉树

BTNode* CreateBinaryTreePI(const char* pstr, const char* istr,int n)
{
    BTNode* s = NULL;
    if (n > 0)
    {
        s = new(BTNode);
        s->data = pstr[0];
        int pos = Find(istr, n, pstr[0]);
        if (pos == -1)exit(1);
        s->lchild = CreateBinaryTreePI(pstr+1, istr, pos);//先序遍历的下一个到其左子树结束一共pos个
        s->rchild = CreateBinaryTreePI(pstr+pos+1, istr+pos+1, n - pos-1);
    }
    return s;
}
BTNode* CreateBTPI(const char* pstr, const char* istr)
{
    int n = strlen(pstr);
    int m = strlen(istr);
    if (pstr == NULL || istr == NULL || n < 1 || m < 1 || n != m)return NULL;
    return CreateBinaryTreePI(pstr, istr, n);
}

找根的位置

int Find(const char* istr, int n, char ch)
{
    int pos = -1;
    for (int i = 0; i < n; i++)
    {
        if (istr[i] == ch)
        {
            pos = i;
            break;
        }
    }
    return pos;
}

主函数

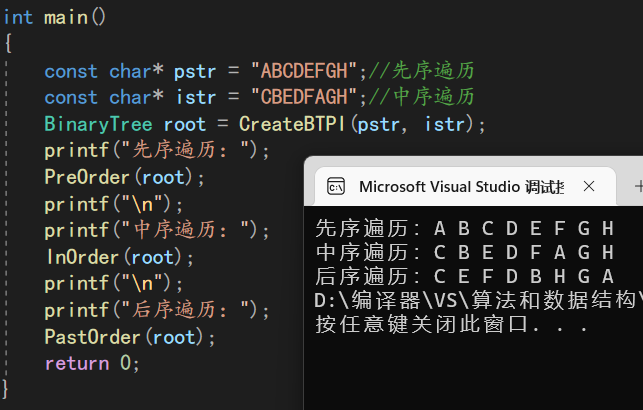
已知先序序列和后序序列，创建二叉树

这跟上面的代码差不多，只是每次划分的范围需要注意。

后序序列的末尾是根，前半部分(0~pos)的pos个是左子树，后半部分(pos+1~n-1)的n-pos-1是右子树,因为末尾是根，所以需要-1；

中序序列用来找根的pos。

BTNode* CreateBinaryTreeIL(const char* istr, const char* lstr, int n)
{
    BTNode* s = NULL;
    if (n > 0)
    {
        s = new(BTNode);
        s->data = lstr[n-1];
        int pos = Find(istr, n, lstr[n-1]);
        if (pos == -1)exit(1);
        s->lchild = CreateBinaryTreeIL(istr, lstr, pos);
        s->rchild = CreateBinaryTreeIL(istr + pos + 1, lstr + pos, n - pos - 1);
    }
    return s;
}
BTNode* CreateBTIL(const char* istr, const char* lstr)
{
    int n = strlen(istr);
    int m = strlen(lstr);
    if (istr == NULL || lstr == NULL || n < 1 || m < 1 || n != m)return NULL;
    return CreateBinaryTreeIL(istr, lstr, n);
}

主函数