第五章 深度学习
十三、自然语言处理(NLP)
4. 语言模型
4.1 什么是语言模型
语言模型在文本处理、信息检索、机器翻译、语音识别中承担这重要的任务。从通俗角度来说,语言模型就是通过给定的一个词语序列,预测下一个最可能的词语是什么。传统语言模型有N-gram模型、HMM(隐马尔可夫模型)等,进入深度学习时代后,著名的语言模型有神经网络语言模型(Neural Network Language Model,NNLM),循环神经网络(Recurrent Neural Networks,RNN)等。
语言模型从概率论专业角度来描述就是:为长度为m的字符串确定其概率分布 P ( w 1 , w 2 , . . . , w n ) P(w_1, w_2, ..., w_n) P(w1,w2,...,wn),其中 w 1 w_1 w1到 w n w_n wn依次表示文本中的各个词语。一般采用链式法则计算其概率值:
P ( w 1 , w 2 , . . . , w n ) = P ( w 1 ) P ( w 2 ∣ w 1 ) P ( w 3 ∣ w 1 , w 2 ) . . . P ( w m ∣ w 1 , w 2 , . . . , w m − 1 ) P(w_1, w_2, ..., w_n) = P(w_1)P(w_2|w_1)P(w_3|w_1,w_2)...P(w_m|w_1,w_2,...,w_{m-1}) P(w1,w2,...,wn)=P(w1)P(w2∣w1)P(w3∣w1,w2)...P(wm∣w1,w2,...,wm−1)
观察上式,可发现,当文本长度过长时计算量过大,所以有人提出N元模型(N-gram)降低计算复杂度。
4.2 N-gram模型
所谓N-gram(N元)模型,就是在计算概率时,忽略长度大于N的上下文词的影响。当N=1时,称为一元模型(Uni-gram Mode),其表达式为:
P ( w 1 , w 2 , . . . , w n ) = ∏ i = 1 m P ( w i ) P(w_1, w_2, ..., w_n) = \prod_{i=1}^m P(w_i) P(w1,w2,...,wn)=i=1∏mP(wi)
当N=2时,称为二元模型(Bi-gram Model),其表达式为:
P ( w 1 , w 2 , . . . , w n ) = ∏ i = 1 m P ( w i ∣ w i − 1 ) P(w_1, w_2, ..., w_n) = \prod_{i=1}^m P(w_i|w_{i-1}) P(w1,w2,...,wn)=i=1∏mP(wi∣wi−1)
当N=3时,称为三元模型(Tri-gram Model),其表达式为:
P ( w 1 , w 2 , . . . , w n ) = ∏ i = 1 m P ( w i ∣ w i − 2 , w i − 1 ) P(w_1, w_2, ..., w_n) = \prod_{i=1}^m P(w_i|w_{i-2}, w_{i-1}) P(w1,w2,...,wn)=i=1∏mP(wi∣wi−2,wi−1)
可见,N值越大,保留的词序信息(上下文)越丰富,但计算量也呈指数级增长。
4.3 神经网络语言模型(NNLM)
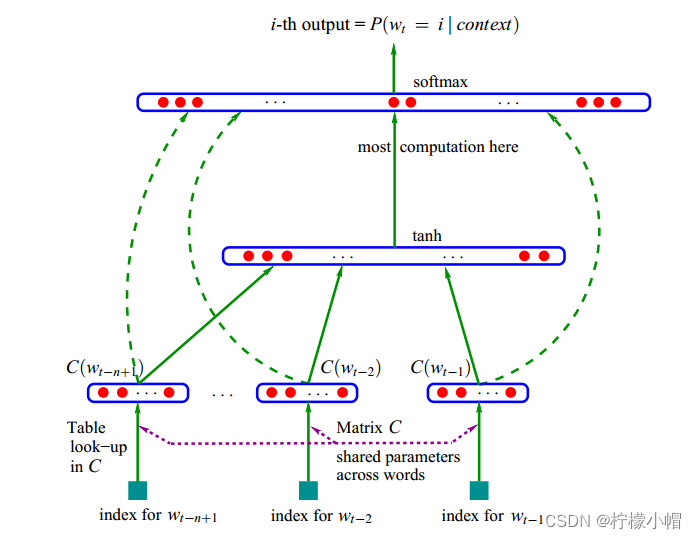
NNLM是利用神经网络对N元条件进行概率估计的一种方法,其基本结构如下图所示:
-
输入:前N-1个词语的向量
-
输出:第N个词语的一组概率
-
目标函数:
f ( w t , t t − 1 , . . . , w t − n + 1 ) = p ( p t ∣ w 1 t − 1 ) f(w_t, t_{t-1}, ..., w_{t-n+1}) = p(p_t|w_1^{t-1}) f(wt,tt−1,...,wt−n+1)=p(pt∣w1t−1)
其中, w t w_t wt表示第t个词, w 1 t − 1 w_1^{t-1} w1t−1表示第1个到第t个词语组成的子序列,每个词语概率均大于0,所有词语概率之和等于1。该模型计算包括两部分:特征映射、计算条件概率
- 特征映射:将输入映射为一个特征向量,映射矩阵 C ∈ R ∣ V ∣ × m C \in R^{|V| \times m} C∈R∣V∣×m
- 计算条件概率分布:通过另一个函数,将特征向量转化为一个概率分布
神经网络计算公式为:
h = t a n h ( H x + b ) y = U h + d h = tanh(Hx + b) \\ y = Uh + d h=tanh(Hx+b)y=Uh+d
H为隐藏层权重矩阵,U为隐藏层到输出层的权重矩阵。输出层加入softmax函数,将y转换为对应的概率。模型参数 θ \theta θ,包括:
θ = ( b , d , H , U , C ) \theta = (b, d, H, U, C) θ=(b,d,H,U,C)
以下是一个计算示例:设词典大小为1000,向量维度为5,N=3,先将前N个词表示成独热向量:
呼:[1,0,0,0,0]
伦:[0,1,0,0,0]
贝:[0,0,1,0,0]
输入矩阵为:[3, 5]
权重矩阵:[1000, 5]
隐藏层:[3, 5] * [1000, 5] = [3, 5]
输出层权重:[5, 1000]
输出矩阵:[3, 5] * [5, 1000] = [3, 1000] ==> [1, 1000],表示预测属于1000个词的概率.
4.4 Word2vec
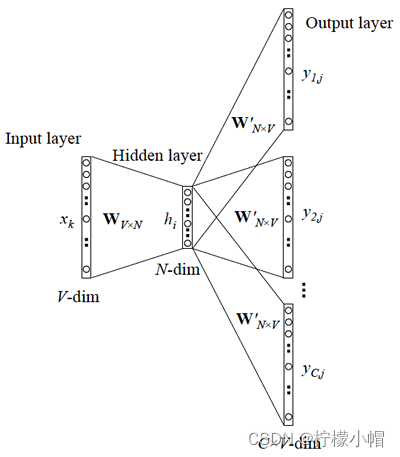
Word2vec是Goolge发布的、应用最广泛的词嵌入表示学习技术,其主要作用是高效获取词语的词向量,目前被用作许多NLP任务的特征工程。Word2vec 可以根据给定的语料库,通过优化后的训练模型快速有效地将一个词语表达成向量形式,为自然语言处理领域的应用研究提供了新的工具,包含Skip-gram(跳字模型)和CBOW(连续词袋模型)来建立词语的词嵌入表示。Skip-gram的主要作用是根据当前词,预测背景词(前后的词);CBOW的主要作用是根据背景词(前后的词)预测当前词。
4.4.1 Skip-gram
Skip-gram的主要作用是根据当前词,预测背景词(前后的词),其结构图如下图所示:
例如有如下语句:呼伦贝尔大草原
呼_ _ 尔_ _原
_伦_ _大_ _
_ _贝_ _ 草_
呼_ _尔_ _原
_伦_ _大_ _
预测出前后词的数量,称为window_size(以上示例中windows_size为2),实际是要将以下概率最大化:
P(伦|呼)P(贝|呼)
P(伦|尔)P(贝|尔) P(大|尔)P(草|尔)
P(大|原)P(草|原)
......
可以写出概率的一般化表达式,设有文本Text,由N个单词组成:
T e x t = w 1 , w 2 , w 3 , . . . , w n Text = {w_1, w_2, w_3, ..., w_n} Text=w1,w2,w3,...,wn
目标函数可以写作:
a r g m a x ∏ c ∈ T e x t ∏ c ∈ c ( w ) P ( c ∣ w ; θ ) argmax \prod_{c \in Text} \prod_{c \in c(w)} P(c|w; \theta) argmaxc∈Text∏c∈c(w)∏P(c∣w;θ)
因为概率均为0~1之间的数字,连乘计算较为困难,所以转换为对数相加形式:
a r g m a x ∑ c ∈ T e x t ∑ c ∈ c ( w ) l o g P ( c ∣ w ; θ ) argmax \sum_{c \in Text} \sum_{c \in c(w)} logP(c|w;\theta) argmaxc∈Text∑c∈c(w)∑logP(c∣w;θ)
再表示为softmax形式:
a r g m a x ∑ c ∈ T e x t ∑ c ∈ c ( w ) l o g e u c ⋅ v w ∑ c ′ ∈ v o c a b e c ′ ⋅ v w argmax \sum_{c \in Text} \sum_{c \in c(w)} log \frac{e^{u_c \cdot v_w}}{\sum_{c' \in vocab }e_{c'} \cdot v_w} argmaxc∈Text∑c∈c(w)∑log∑c′∈vocabec′⋅vweuc⋅vw
其中,U为上下文单词矩阵,V为同样大小的中心词矩阵,因为每个词可以作为上下文词,同时也可以作为中心词,再将如上公式进一步转化:
a r g m a x ∑ c ∈ T e x t ∑ c ∈ c ( w ) u c ⋅ v w − l o g ∑ c ′ ∈ v o c a b e c ′ ⋅ v w argmax \sum_{c \in Text} \sum_{c \in c(w)} u_c \cdot v_w - log \sum_{c' \in vocab }e_{c'} \cdot v_w argmaxc∈Text∑c∈c(w)∑uc⋅vw−logc′∈vocab∑ec′⋅vw
上式中,由于需要在整个词汇表中进行遍历,如果词汇表很大,计算效率会很低。所以,真正进行优化时,采用另一种优化形式。例如有如下语料库:
文本:呼伦贝尔大草原
将window_size设置为1,构建正案例词典、负案例词典(一般来说,负样本词典比正样本词典大的多):
正样本:D = {(呼,伦),(伦,呼),(伦,贝),(贝,伦),(贝,尔),(尔,贝),(尔,大),(大,尔),(大,草)(草,大),(草,原),(原,草)}
负样本:D’= {(呼,贝),(呼,尔),(呼,大),(呼,草),(呼,原),(伦,尔),(伦,大),(伦,草),(伦,原),(贝,呼),(贝,大),(贝,草),(贝,原),(尔,呼),(尔,伦)(尔,草),(尔,原),(大,呼),(大,伦),(大,原),(草,呼),(草,伦),(草,贝),(原,呼),(原,伦),(原,贝),(原,尔),(原,大)}
词向量优化的目标函数定义为正样本、负样本公共概率最大化函数:
a r g m a x ( ∏ w , c ∈ D l o g P ( D = 1 ∣ w , c ; θ ) ∏ w , c ∈ D ′ P ( D = 0 ∣ w , c ; θ ) ) = a r g m a x ( ∏ w , c ∈ D 1 1 + e x p ( − U c ⋅ V w ) ∏ w , c ∈ D ′ [ 1 − 1 1 + e x p ( − U c ⋅ V w ) ] ) = a r g m a x ( ∑ w , c ∈ D l o g σ ( U c ⋅ V w ) + ∑ w , c ∈ D ′ l o g σ ( − U c ⋅ V w ) ) argmax (\prod_{w,c \in D} log P(D=1|w,c; \theta) \prod_{w, c \in D'} P(D=0|w, c; \theta)) \\ = argmax (\prod_{w,c \in D} \frac{1}{1+exp(-U_c \cdot V_w)} \prod_{w, c \in D'} [1- \frac{1}{1+exp(-U_c \cdot V_w)}]) \\ = argmax(\sum_{w,c \in D} log \sigma (U_c \cdot V_w) + \sum_{w,c \in D'} log \sigma (-U_c \cdot V_w)) argmax(w,c∈D∏logP(D=1∣w,c;θ)w,c∈D′∏P(D=0∣w,c;θ))=argmax(w,c∈D∏1+exp(−Uc⋅Vw)1w,c∈D′∏[1−1+exp(−Uc⋅Vw)1])=argmax(w,c∈D∑logσ(Uc⋅Vw)+w,c∈D′∑logσ(−Uc⋅Vw))
在实际训练时,会从负样本集合中选取部分样本(称之为“负采样”)来进行计算,从而降低运算量.要训练词向量,还需要借助于语言模型.
4.4.2 CBOW模型
CBOW模型全程为Continous Bag of Words(连续词袋模型),其核心思想是用上下文来预测中心词,例如:
呼伦贝_大草原
其模型结构示意图如下:
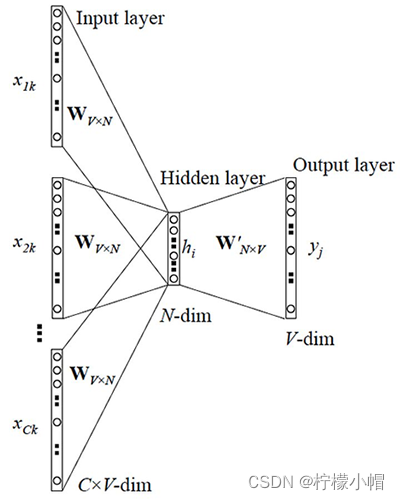
- 输入: C × V C \times V C×V的矩阵,C表示上下文词语的个数,V表示词表大小
- 隐藏层: V × N V \times N V×N的权重矩阵,一般称为word-embedding,N表示每个词的向量长度,和输入矩阵相乘得到 C × N C \times N C×N的矩阵。综合考虑上下文中所有词信息预测中心词,所以将 C × N C \times N C×N矩阵叠加,得到 1 × N 1 \times N 1×N的向量
- 输出层:包含一个 N × V N \times V N×V的权重矩阵,隐藏层向量和该矩阵相乘,输出 1 × V 1 \times V 1×V的向量,经过softmax转换为概率,对应每个词表中词语的概率
4.4.3 示例:训练词向量
数据集:来自中文wiki文章
代码:建议在AIStudio下执行
- 安装gensim
!pip install gensim==3.8.1 # 如果不在AIStudio下执行去掉前面的叹号
- 用于解析XML,读取XML文件中的数据,并写入到新的文本文件中
import logging
import os.path
import os
from gensim.corpora import WikiCorpus
# 1. 获取输入数据路径
inp = 'data/data104767/articles.xml.bz2'
# 2. 创建新的文本文件(输出文件)
outp = open('wiki.zh.text','w',encoding='utf-8')
# 3. 调用gensim读取xml压缩文件
count = 0
wiki = WikiCorpus(inp, lemmatize=False, dictionary={})
for text in wiki.get_texts():
outp.write( " ".join(text) + "\n")
count += 1
if count % 200 == 0:
print("count:", count)
if count % 20000 == 0:
break
outp.close()
print("Finished Saved " +str(count) + " articles")
- 生成分词文件
import jieba
import jieba.analyse
import codecs # python封装的文件的工具包
def process_wiki_text(origin_file,target_file):
with codecs.open(origin_file, 'r','utf-8') as inp, codecs.open(target_file,'w','utf-8') as outp:
line = inp.readline()
num = 1
while line:
line_seg = " ".join(jieba.cut(line))
outp.writelines(line_seg)
num += 1
line = inp.readline()
print('----', num, ' articles----')
inp.close()
outp.close()
process_wiki_text('wiki.zh.text','wiki.zh.text.seg')
- 训练
# 导入工具库
import logging
import sys
import multiprocessing # cpu开启多线程执行
from gensim.models import Word2Vec
# 按照行的方式读取文件内容(分词文件)
from gensim.models.word2vec import LineSentence
logger = logging.getLogger(__name__)
# format: 指定输出的格式和内容,format可以输出很多有用信息,
# %(asctime)s: 打印日志的时间
# %(levelname)s: 打印日志级别名称
# %(message)s: 打印日志信息
logging.basicConfig(format='%(asctime)s: %(levelname)s: %(message)s')
logging.root.setLevel(level=logging.INFO)
# 1.输入文件
inp = 'wiki.zh.text.seg'
# 2.输出文件
outp1 = 'wiki.zh.text.model' # 模型
outp2 = 'wiki.zh.text.vector' # 权重
# 3.模型的训练和保存
model = Word2Vec(
LineSentence(inp),
size=100, # 词向量的维度(25~1000)
window=3,
min_count=5, # 如果语料库中单词出现的次数小于5,就忽略该单词
workers=multiprocessing.cpu_count()
)
model.save(outp1)
model.wv.save_word2vec_format(outp2,binary=False)
- 测试
import gensim
from gensim.models import Word2Vec
# 1. 加载模型
model = Word2Vec.load('whik.zh.text.model')
count = 0
# 2. 变量单词和对应的向量
count = 0
for word in model.wv.index2word:
print(word, model[word])
count += 1
if count==10:
break
print("==============================================")
result = model.most_similar(u"铁路")
for r in result:
print(r)
print("==============================================")
result2 = model.most_similar(u"中药")
for r in result2:
print(r)
输出(训练过程略):
('高速铁路', 0.8310302495956421)
('客运专线', 0.8245105743408203)
('高铁', 0.8095601201057434)
('城际', 0.802475094795227)
('联络线', 0.7837506532669067)
('成昆铁路', 0.7820425033569336)
('支线', 0.7775323390960693)
('通车', 0.7751388549804688)
('沪', 0.7748854756355286)
('京广', 0.7708789110183716)
==============================================
('草药', 0.9046826362609863)
('中药材', 0.8511005640029907)
('气功', 0.8384993672370911)
('中医学', 0.8368280529975891)
('调味', 0.8364394307136536)
('冶炼', 0.8328938484191895)
('药材', 0.8304706811904907)
('有机合成', 0.8298543691635132)
('针灸', 0.8297436833381653)
('药用', 0.8281913995742798)
4.5 循环神经网络(RNN)
前面提到的关于NLP的模型及应用,都未考虑词的顺序问题,而在自然语言中,词语顺序又是极其重要的特征。循环神经网络(Recurrent Neural Network,RNN)能够在原有神经网络的基础上增加记忆单元,处理任意长度的序列(理论上),并且在前后词语(或字)之间建立起依赖关系。相比于CNN,RNN更适合处理视频、语音、文本等与时序相关的问题。
4.5.1 原生RNN
4.5.1.1 RNN起源及发展
1982年,物理学家约翰·霍普菲尔德(John Hopfield)利用电阻、电容和运算放大器等元件组成的模拟电路实现了对网络神经元的描述,该网络从输出到输入有反馈连接。1986年,迈克尔·乔丹(Michael Jordan,不是打篮球那哥们,而是著名人工智能学者、美国科学院院士、吴恩达的导师)借鉴了Hopfield网络的思想,正式将循环连接拓扑结构引入神经网络。1990年,杰弗里·埃尔曼(Jeffrey Elman)又在Jordan的研究基础上做了部分简化,正式提出了RNN模型(那时还叫Simple Recurrent Network,SRN)。
4.5.1.2 RNN的结构
RNN结构如下图所示:
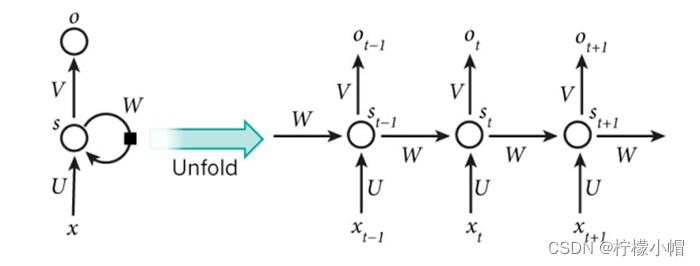
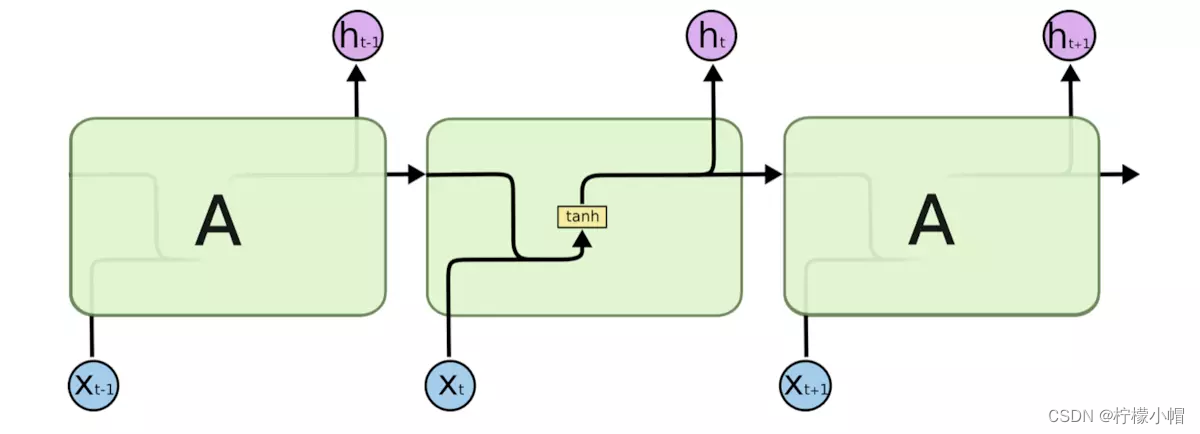
上图中,左侧为不展开的画法,右侧为展开画法。内部结构如下图所示:
计算公式可表示为:
s t = f ( U ⋅ x t + W ⋅ s t − 1 + b ) y t = g ( V ⋅ s t + d ) s_t = f(U \cdot x_t + W \cdot s_{t-1} + b) \\ y_t = g(V \cdot s_t + d) st=f(U⋅xt+W⋅st−1+b)yt=g(V⋅st+d)
其中, x t x_t xt表示 t t t时刻的输入; s t s_t st表示 t t t时刻隐藏状态; f f f和 g g g表示激活函数; U , V , W U,V,W U,V,W分别表示输入层 → 隐藏层权重、隐藏层 → 输出层权重、隐藏层 → 隐藏层权重。对于任意时刻 t t t,所有权重和偏置都共享,这极大减少了模型参数量。
计算时,首先利用前向传播算法,依次按照时间顺序进行计算,再利用反向传播算法进行误差传递,和普通BP(Back Propagation)网络唯一区别是,加入了时间顺序,计算方式有些微差别,称为BPTT(Back Propagation Through Time)算法。
4.5.1.3 RNN的功能
RNN善于处理跟序列相关的信息,如:语音识别,语言建模,翻译,图像字幕。它能根据近期的一些信息来执行/判别/预测当前任务。例如:
白色的云朵漂浮在蓝色的____
天空中飞过来一只___
根据前面输入的一连串词语,可以预测第一个句子最后一个词为"天空"、第二个句子最后一个词为"鸟"的概率最高。
4.5.1.4 RNN的缺陷
因为计算的缘故,RNN容易出现梯度消失,导致它无法学习过往久远的信息,无法处理长序列、远期依赖任务。例如:
我生长在中国,祖上十代都是农民,家里三亩一分地。我是家里老三,我大哥叫大狗子,二哥叫二狗子,我叫三狗子,我弟弟叫狗窝子。我的母语是_____
要预测出句子最后的词语,需要根据句子开够的信息"我出生在中国",才能确定母语是"中文"或"汉语"的概率最高。原生RNN在处理这类远期依赖任务时出现了困难,于是LSTM被提出。
4.5.2 长短期记忆模型(LSTM)
长短期记忆模型(Long Short Term Memory,LSTM)是RNN的变种,于1997年Schmidhuber和他的合作者Hochreiter提出,由于独特的设计结构,LSTM可以很好地解决梯度消失问题,能够处理更长的序列,更好解决远期依赖任务。LSTM非常适合构造大型深度神经网络。2009年,用改进版的LSTM,赢得了国际文档分析与识别大赛(ICDAR)手写识别大赛冠军;2014年,Yoshua Bengio的团队提出了一种更好的LSTM变体GRU(Gated Recurrent Unit,门控环单元);2016年,Google利用LSTM来做语音识别和文字翻译;同年,苹果公司使用LSTM来优化Siri应用。
LSTM同样具有链式结构,它具有4个以特殊方式互相影响的神经网络层。其结构入下图所示:
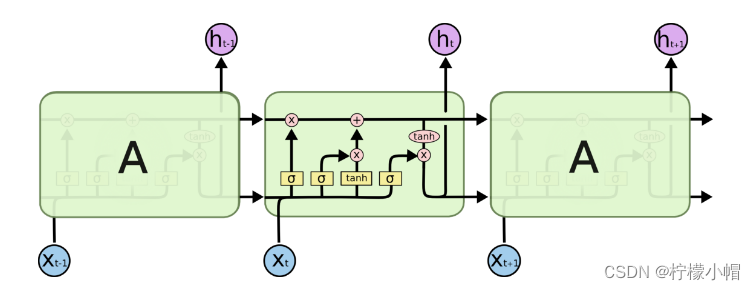
LSTM的核心是细胞状态,用贯穿细胞的水平线表示。细胞状态像传送带一样。它贯穿整个细胞却只有很少的分支,这样能保证信息不变的流过整个结构。同时,LSTM通过称为门(gate)的结构来对单元状态进行增加或删除,包含三扇门:
-
遗忘门:决定哪些信息丢弃
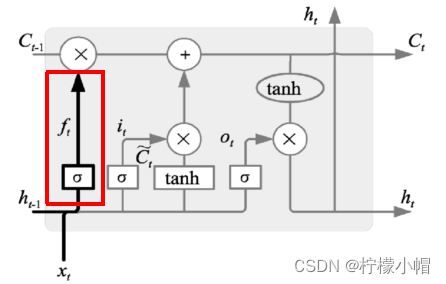
表达式为: f t = σ ( W f ⋅ [ h t − 1 , x t ] + b f ) f_t = \sigma (W_f \cdot [h_{t-1}, x_t] + b_f) ft=σ(Wf⋅[ht−1,xt]+bf),当输出为1时表示完全保留,输出为0是表示完全丢弃
-
输入门:决定哪些信息输入进来
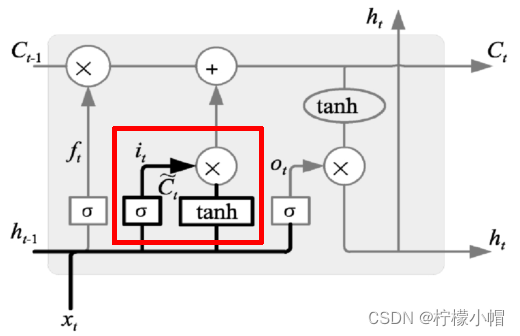
表达式为:
i t = σ ( W i ⋅ [ h t − 1 , x t ] + b i ) C ~ t = t a n h ( W c ⋅ [ h t − 1 , x t ] + b c ) i_t = \sigma (W_i \cdot [h_{t-1}, x_t] + b_i) \\ \tilde{C}_t = tanh(W_c \cdot [h_{t-1}, x_t] + b_c) it=σ(Wi⋅[ht−1,xt]+bi)C~t=tanh(Wc⋅[ht−1,xt]+bc)
根据输入、遗忘门作用结果,可以对细胞状态进行更新,如下图所示:
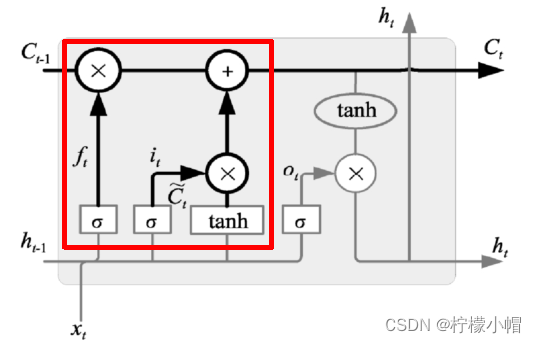
状态更新表达式为:
C t = f t ⋅ C t − 1 + i t ⋅ C ~ t C_t = f_t \cdot C_{t-1} + i_t \cdot \tilde{C}_t Ct=ft⋅Ct−1+it⋅C~t
遗忘门找到了需要忘掉的信息 f t f_t ft后,再将它与旧状态相乘,丢弃掉确定需要丢弃的信息。再将结果加上 i t ⋅ C t i_t \cdot C_t it⋅Ct使细胞状态获得新的信息,这样就完成了细胞状态的更新。
-
输出门:决定输出哪些信息

输出门表达式为:
O t = σ ( W o ⋅ [ h t − 1 , x t ] + b o ) h t = O t ⋅ t a n h ( C t ) O_t = \sigma (W_o \cdot [h_{t-1}, x_t] + b_o) \\ h_t = O_t \cdot tanh(C_t) Ot=σ(Wo⋅[ht−1,xt]+bo)ht=Ot⋅tanh(Ct)
在输出门中,通过一个Sigmoid层来确定哪部分的信息将输出,接着把细胞状态通过Tanh进行处理(得到一个在-1~1之间的值)并将它和Sigmoid门的输出相乘,得出最终想要输出的那部分。
4.5.3 双向循环神经网络
双向循环神经网络(BRNN)由两个循环神经网络组成,一个正向、一个反向,两个序列连接同一个输出层。正向RNN提取正向序列特征,反向RNN提取反向序列特征。例如有如下两个语句:
我喜欢苹果,比安卓用起来更流畅些
我喜欢苹果,基本上每天都要吃一个
根据后面的描述,我们可以得知,第一句中的"苹果"指的是苹果手机,第二句中的"苹果"指的是水果。双向循环神经网络结构如下图所示:
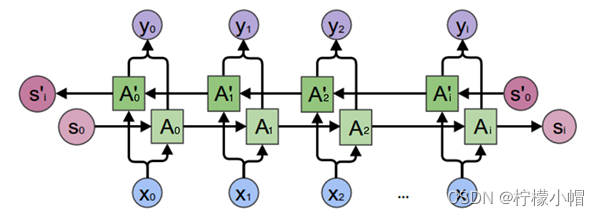
权重设置如下图所示:

计算表达式为:
h t = f ( w 1 x t + w 2 h t − 1 ) h t ′ = f ( w 3 x t + w 5 h t + 1 ′ ) o t = g ( w 4 h t + w 6 h t ′ ) h_t = f(w_1x_t + w_2h_{t-1}) \\ h_t' = f(w_3x_t + w_5h'_{t+1}) \\ o_t = g(w_4h_t + w_6h'_t) ht=f(w1xt+w2ht−1)ht′=f(w3xt+w5ht+1′)ot=g(w4ht+w6ht′)
其中, h t h_t ht为 t t t时刻正向序列计算结果, h t ′ h'_t ht′为 t t t时刻反向序列的计算结果,将正向序列、反向序列结果和各自权重矩阵相乘,相加后结果激活函数产生 t t t时刻的输出。
通常情况下,双向循环神经网络能获得比单向网络更好的性能。