1、前言
点云中近邻点搜索查询是一种非常常见的数据处理操作步骤,近邻点搜索方式包括k近邻搜索、近距离搜索(球体近邻搜索)、圆柱体搜索三种方式,每一种搜索方式适用的场景各不相同。其中kdtree搜索是一种有效搜索近邻点方式,其是一种在k维空间中存储点集的数据结构,它主要用于多维空间的查询,如范围查询和最近邻查询。KD树是一种特殊的二叉树,每个节点表示一个k维数据点。本博客介绍基于python语言的kdtree搜索近邻点,其中scipy库中有kdtree,可以直接近邻近邻点搜索。
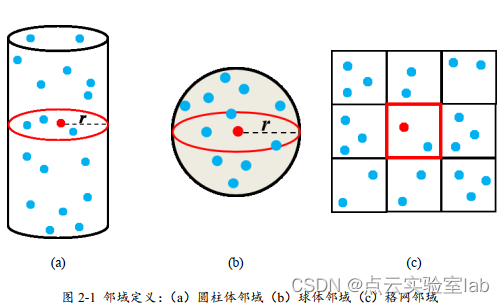
3种近邻点搜索示意图
2 近邻点搜索示例
scipy.spatial模块中的KDTree类是Python中实现KD树的一个库。它提供了高效的方法来进行多维空间的最近邻查询、范围查询等。
2.1 k近邻点搜索
k近邻搜索是指给定待查询点,搜索距离该点最近的k个近邻点,其主要使用query函数实现k近邻查询。代码如下,对于待搜索点querypt,使用kdtree搜索距离其最近的50个近邻点,命令为nearest_dist, nearest_idx = kdtree.query(querypt,k=50)。根据索引nearest_idx得到最近的50个近邻点。
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from scipy.spatial import KDTree
plt.rcParams['font.sans-serif'] = ['SimHei'] # 使用黑体
plt.rcParams['axes.unicode_minus'] = False # 正确显示负号
with open('E:\\testdata01.txt', 'r') as file:
# 初始化一个列表来存储所有的点
points = []
# 逐行读取数据
for line in file:
# 去除行尾的换行符并分割字符串
x, y, z, L = line.strip().split()
# 将字符串转换为浮点数
x = float(x)
y = float(y)
z = float(z)
# 将点添加到列表中
points.append((x, y, z))
querypt=points[800]
kdtree=KDTree(points) #创建kdtree
nearest_dist, nearest_idx = kdtree.query(querypt,k=50)
nearest_points = [points[i] for i in nearest_idx]
fig=plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(*zip(*points), marker='.', color='blue', s=20)
ax.scatter(*zip(*nearest_points), marker='*', color='red', s=20)
ax.scatter(*zip(*[querypt]), marker='o', color='red', s=30)
ax.set_title("三维点云可视化")
ax.set_xlabel("x轴")
ax.set_ylabel("y轴")
ax.set_zlabel("z轴")
plt.show()
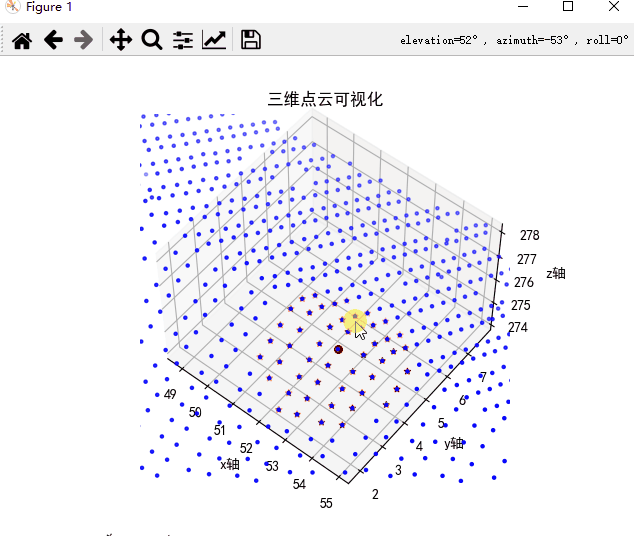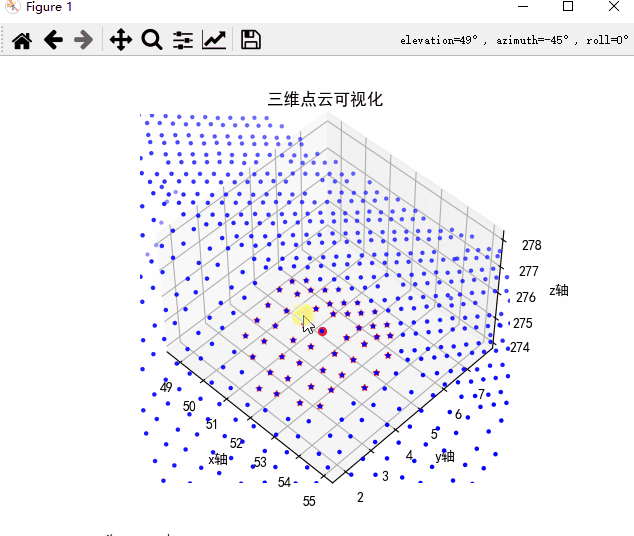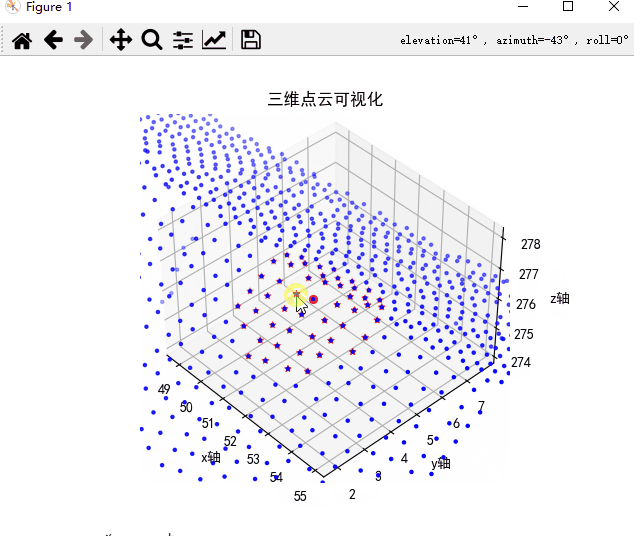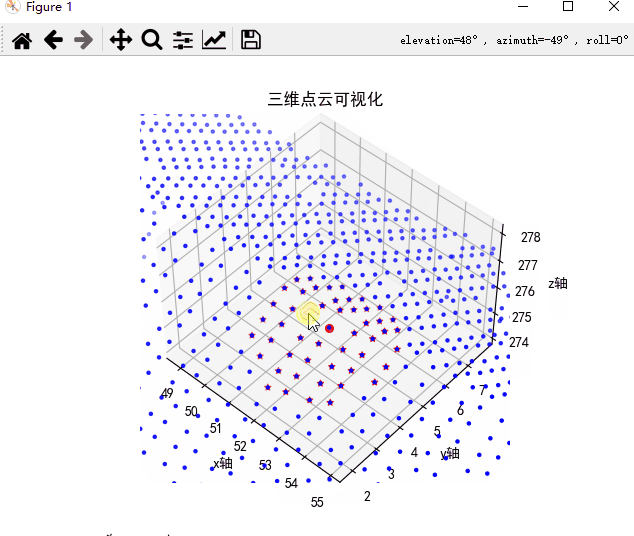
搜索的近邻点,已经按照从近到远进行排序,同时搜索的最近点,是该搜索点自身(如果待搜索点属于kdtree中某一点的话)。搜索近邻点结果如下,红色箭头为待搜索点,搜索的50个点位于该点附近,证明搜索的近邻点正确。
 |  |
2.2 距离近邻点搜索
近距离搜索是搜索距离该点范围内点,即所有点到该点距离均小于该范围,使用函数query_ball_point进行搜索,代码如下,kdtree使用命令nearest_idx = kdtree.query_ball_point(querypt,raduis)进行查询,但是只查询得到距离该点最近点的序号,不包括距离。
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from scipy.spatial import KDTree
plt.rcParams['font.sans-serif'] = ['SimHei'] # 使用黑体
plt.rcParams['axes.unicode_minus'] = False # 正确显示负号
with open('E:\\testdata01.txt', 'r') as file:
# 初始化一个列表来存储所有的点
points = []
# 逐行读取数据
for line in file:
# 去除行尾的换行符并分割字符串
x, y, z, L = line.strip().split()
# 将字符串转换为浮点数
x = float(x)
y = float(y)
z = float(z)
# 将点添加到列表中
points.append((x, y, 0))
querypt=points[800]
kdtree=KDTree(points) #创建kdtree
raduis=1.5
nearest_idx = kdtree.query_ball_point(querypt,raduis)
nearest_points = [points[i] for i in nearest_idx]
fig=plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(*zip(*points), marker='.', color='blue', s=20)
ax.scatter(*zip(*nearest_points), marker='*', color='red', s=20)
ax.scatter(*zip(*[querypt]), marker='o', color='red', s=30)
ax.set_title("三维点云可视化")
ax.set_xlabel("x轴")
ax.set_ylabel("y轴")
ax.set_zlabel("z轴")
plt.show()
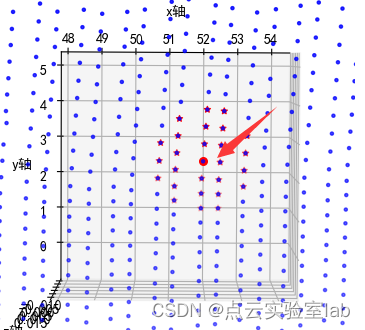
从结果上看,待搜索点为序号为800的点,但是序号为800并没有排在最前面,说明并没有按照由远到近的顺序进行排序,是随机排序。如下图所示,为便于展示,将所有点z坐标均为0,从图可知,所有近邻点位于该点附近,同时所有近邻点近似位于一个圆内,证明距离最近点搜索正确。
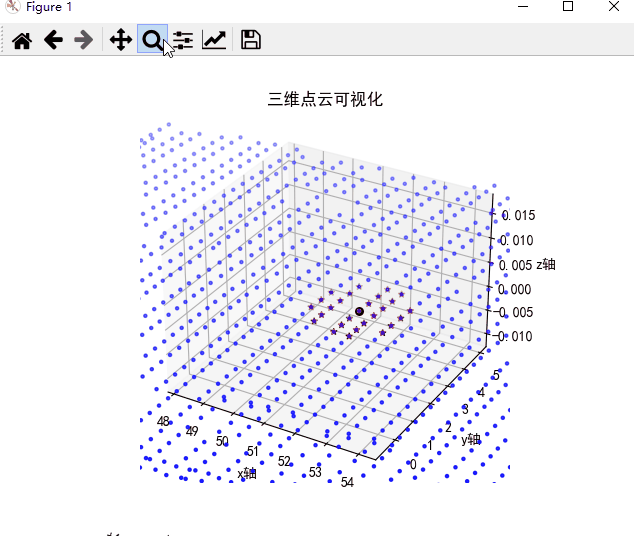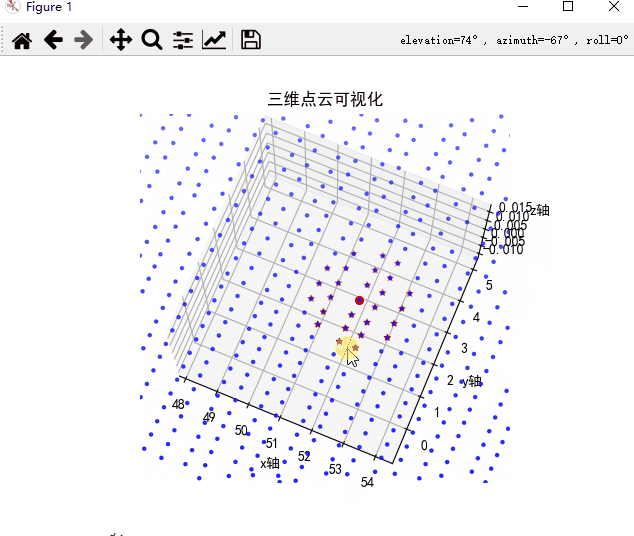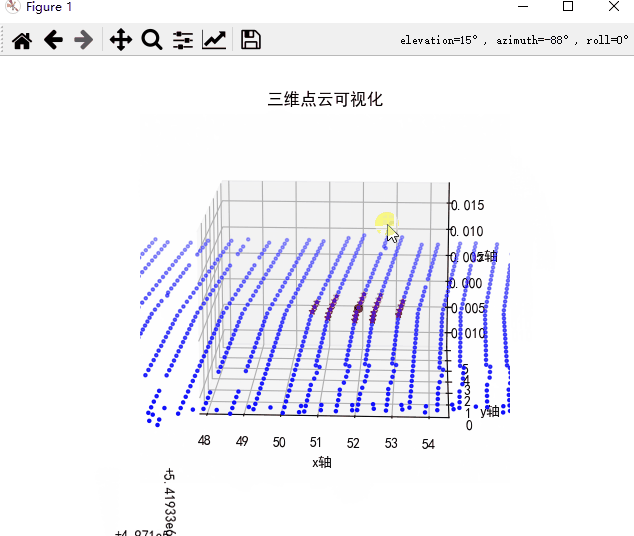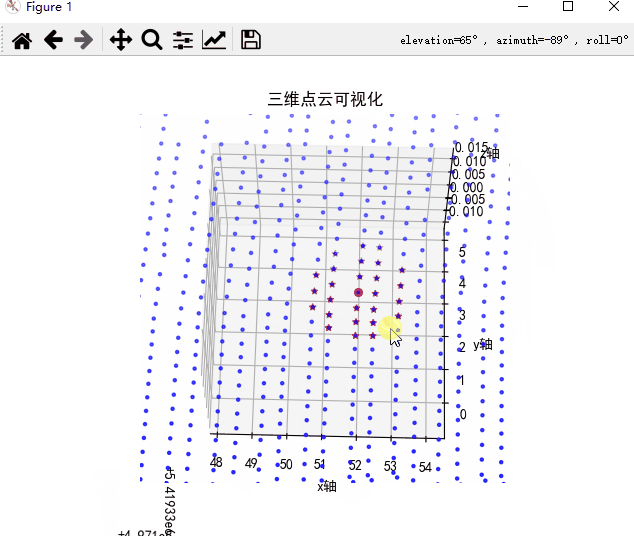 |  |
2.3 圆柱体近邻点搜搜
圆柱体近邻点搜索,即平面二维距离一定,如下图所示,忽略高程上差异。搜索这种近邻点并进行分析,可以得到该点的高程上的结构信息。
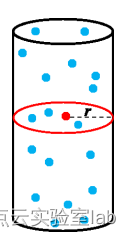
代码如下,其中kdtree搜索时,将所有z坐标设置成0,再使用query_ball_point函数进行搜索得到近邻点,最终实现近邻点搜索。
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from scipy.spatial import KDTree
plt.rcParams['font.sans-serif'] = ['SimHei'] # 使用黑体
plt.rcParams['axes.unicode_minus'] = False # 正确显示负号
with open('E:\\testdata01.txt', 'r') as file:
# 初始化一个列表来存储所有的点
points2D = []
points3D = []
# 逐行读取数据
for line in file:
# 去除行尾的换行符并分割字符串
x, y, z, L = line.strip().split()
# 将字符串转换为浮点数
x = float(x)
y = float(y)
z = float(z)
# 将点添加到列表中
points2D.append((x, y, 0))
points3D.append((x, y, z))
id=100
querypt=points2D[id]
kdtree=KDTree(points2D) #创建kdtree
raduis=2.0
nearest_idx = kdtree.query_ball_point(querypt,raduis)
nearest_points = [points3D[i] for i in nearest_idx]
fig=plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(*zip(*points3D), marker='.', color='blue', s=20)
querypt=points3D[id]
ax.scatter(*zip(*nearest_points), marker='*', color='red', s=20)
ax.scatter(*zip(*[querypt]), marker='o', color='red', s=30)
ax.set_title("三维点云可视化")
ax.set_xlabel("x轴")
ax.set_ylabel("y轴")
ax.set_zlabel("z轴")
plt.show()搜索结果如下,可以发现,对于待搜索点,搜索的圆柱体近邻点,在高程上距离其很远的点,也可以搜索得到,证明圆柱体搜索结果正确。
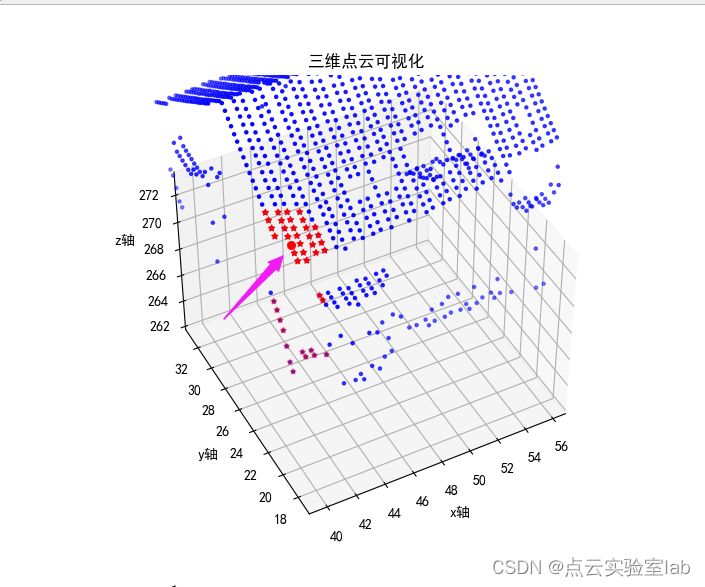
3、小结
本博客介绍了基于python的kdtree的三种近邻点搜索方式,三种方式适用场景不同,可以根据实际需要来选择何种搜索方式。