文章目录
- 离散数学与组合数学-06特殊的图
- 6.1 欧拉图
- 6.1.1 哥尼斯堡七桥问题
- 6.1.2 欧拉图的定义
- 6.1.3 无向欧拉图的判定
- 6.1.4 有向欧拉图的判定
- 6.1.5 一笔画问题
- 6.1.6 求回路
- 6.2 哈密顿图
- 6.2.1 周游世界问题
- 6.2.2 哈密顿图的定义
- 6.2.3 哈密顿图的必要条件
- 6.2.4 哈密顿图的充分条件
- 6.2.5 其它方法
- 6.2.6 哈密顿图的应用
- 6.3 偶图
- 6.3.1 偶图的定义
- 6.3.2 偶图的判定
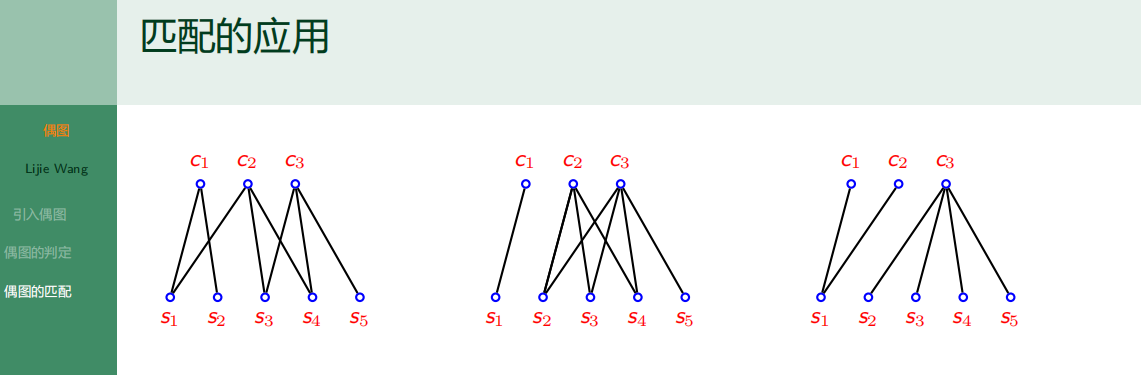
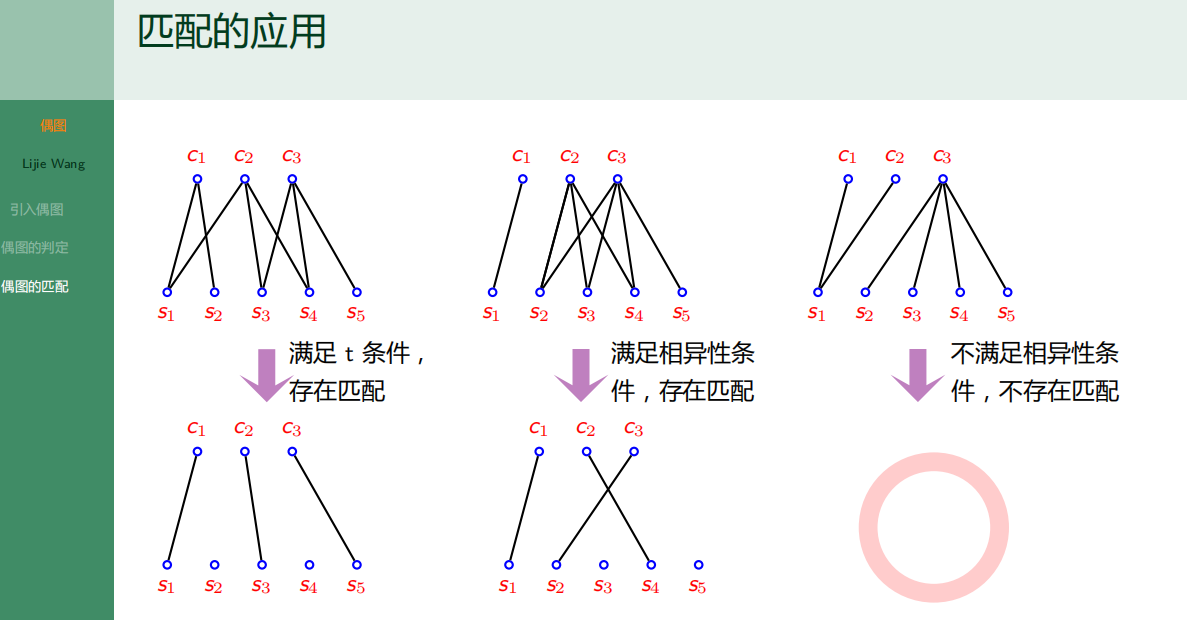
- 6.3.3 偶图的匹配
- 6.4 平面图
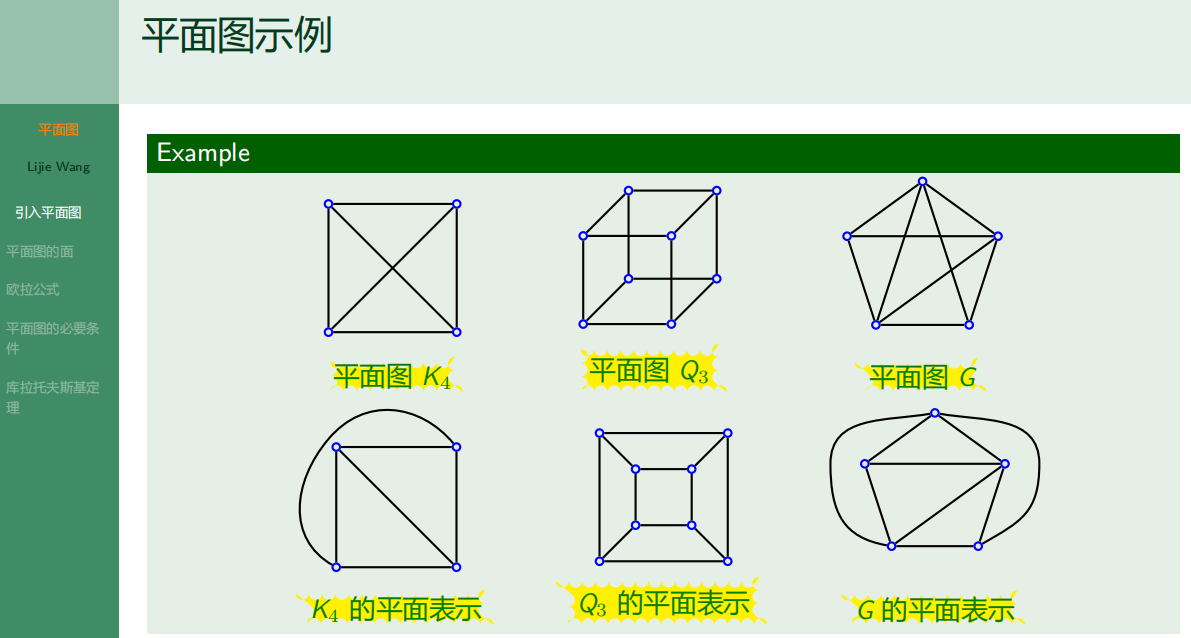
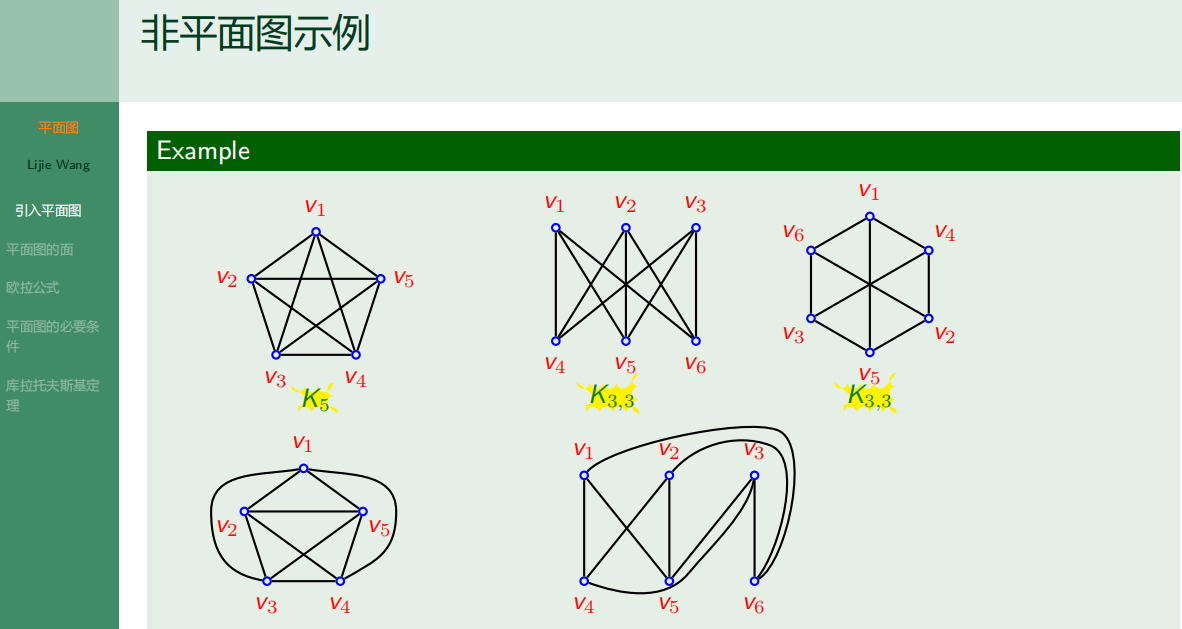
- 6.4.1 平面图的定义
- 6.4.2 平面图的面和边界
- 6.4.3 欧拉公式
- 6.4.4 平面图的必要条件
- 6.4.5 库拉托夫斯基定理
- 同胚
- 收缩
- 库拉托夫斯基定理
本文为离散数据与组合数学电子科技大学王丽杰老师的课程笔记,详细视频参考
【电子科技大学】离散数学(上) 王丽杰
【电子科技大学】离散数学(下) 王丽杰
latex的离散数学写法参考: 离散数学与组合数学-01
离散数学公式
!符号 代码 含义
∧
\wedge
∧ \wedge 且
∨
\vee
∨ \vee 或
∩
\cap
∩ \cap 交
∪
\cup
∪ \cup 并
⊆
\subseteq
⊆ \subseteq 子集
⊈
\nsubseteq
⊈ \nsubseteq 不是子集
⊂
\subset
⊂ \subset 真子集
⊄
\not\subset
⊂ \not\subset 不是真子集
∈
\in
∈ \in 属于
∉
\not\in
∈ \not\in 不属于
↔
\leftrightarrow
↔ \leftrightarrow 等价
⇔
\Leftrightarrow
⇔ \Leftrightarrow 等值
¬
\neg
¬ \neg或\lnot 非
R
\mathbb{R}
R \mathbb{R} 实数集
Z
\mathbb{Z}
Z \mathbb{Z} 整数集
∅
\varnothing
∅ \varnothing 空集
∀
\forall
∀ \forall 对任意的
∃
\exists
∃ \exists 存在
≥
\geq
≥ \geq大于等于
≤
\leq
≤ \leq 小于等于
下标的输入命令是:
x
内容
x_{内容}
x内容 x_{内容}
上标的输入命令式:
x
2
x^2
x2 x^2
空格 \quad
R / R\mkern-10.5mu/ R/ R\mkern-10.5mu/ 数值越大,斜杆越往字母左侧移动
离散数学与组合数学-06特殊的图
6.1 欧拉图
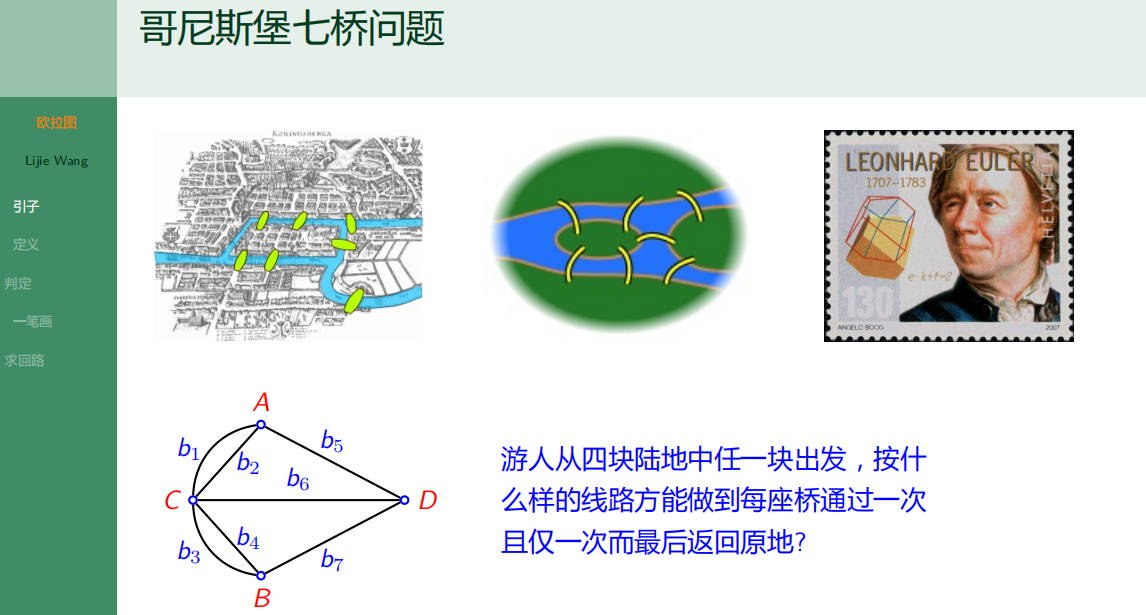
6.1.1 哥尼斯堡七桥问题
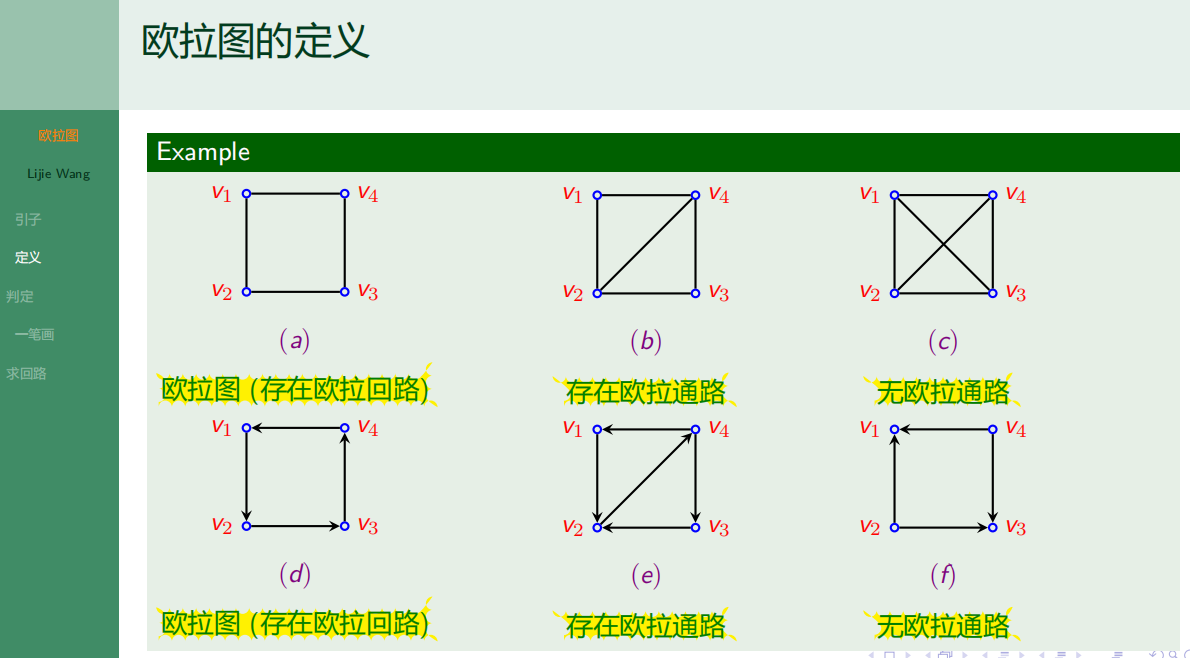
6.1.2 欧拉图的定义

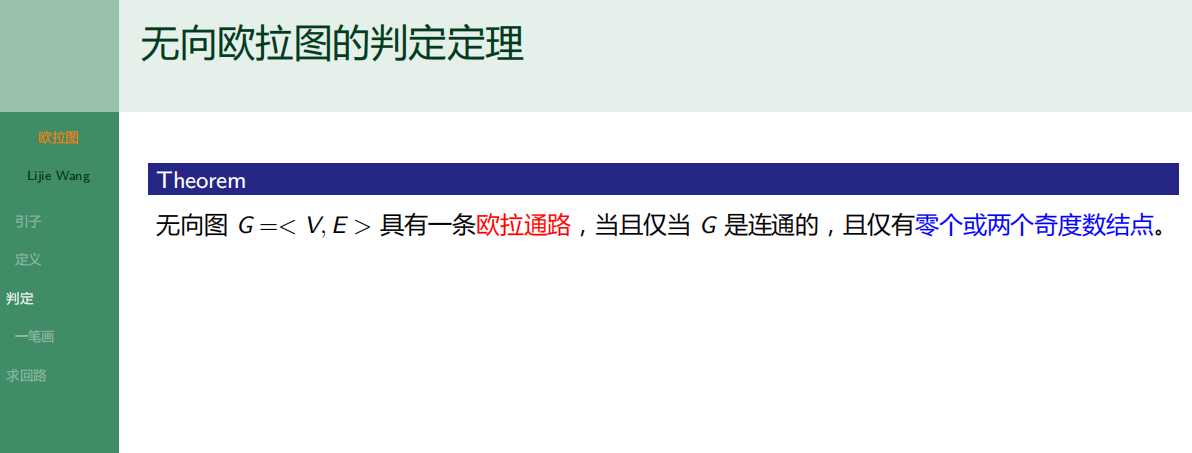
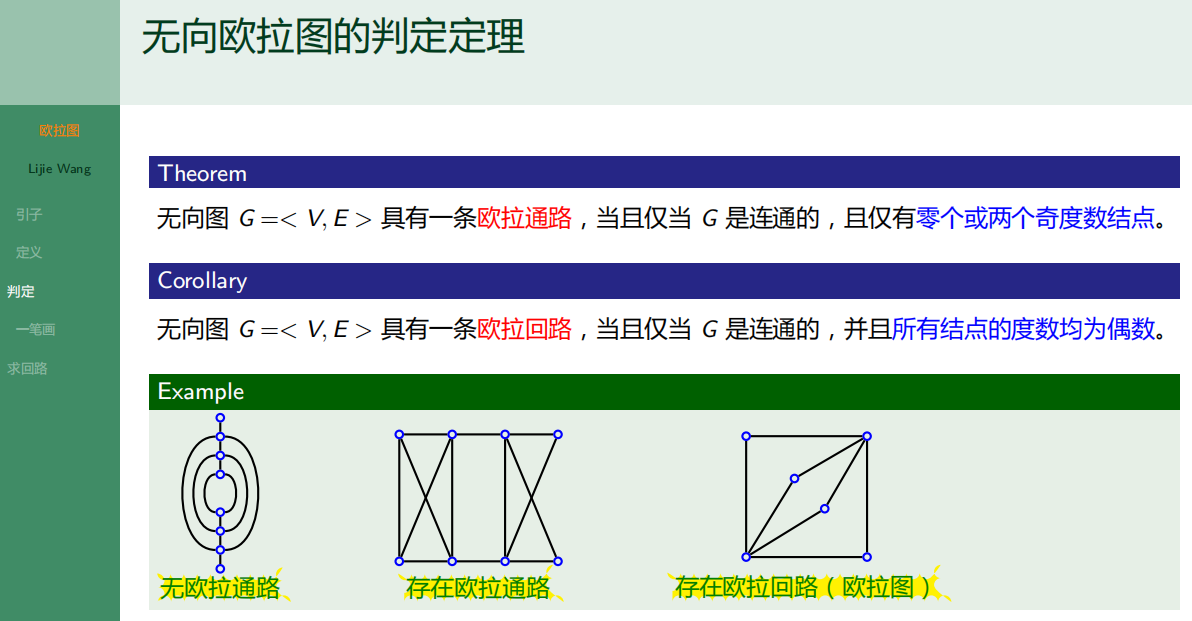
6.1.3 无向欧拉图的判定

6.1.4 有向欧拉图的判定

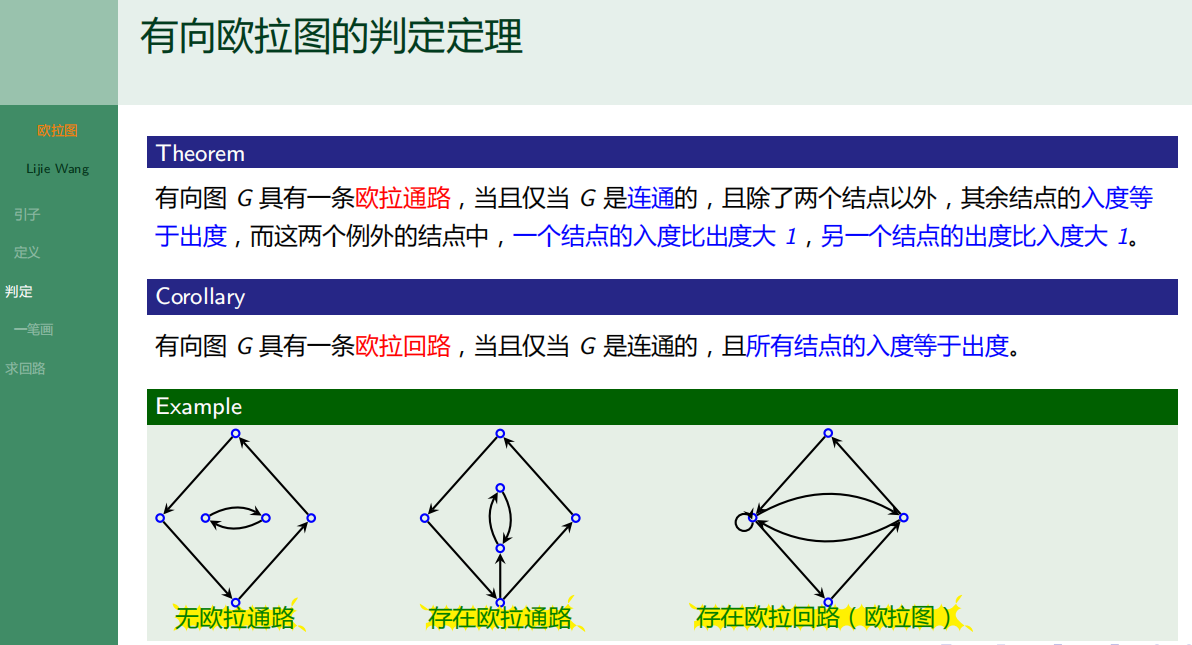
6.1.5 一笔画问题
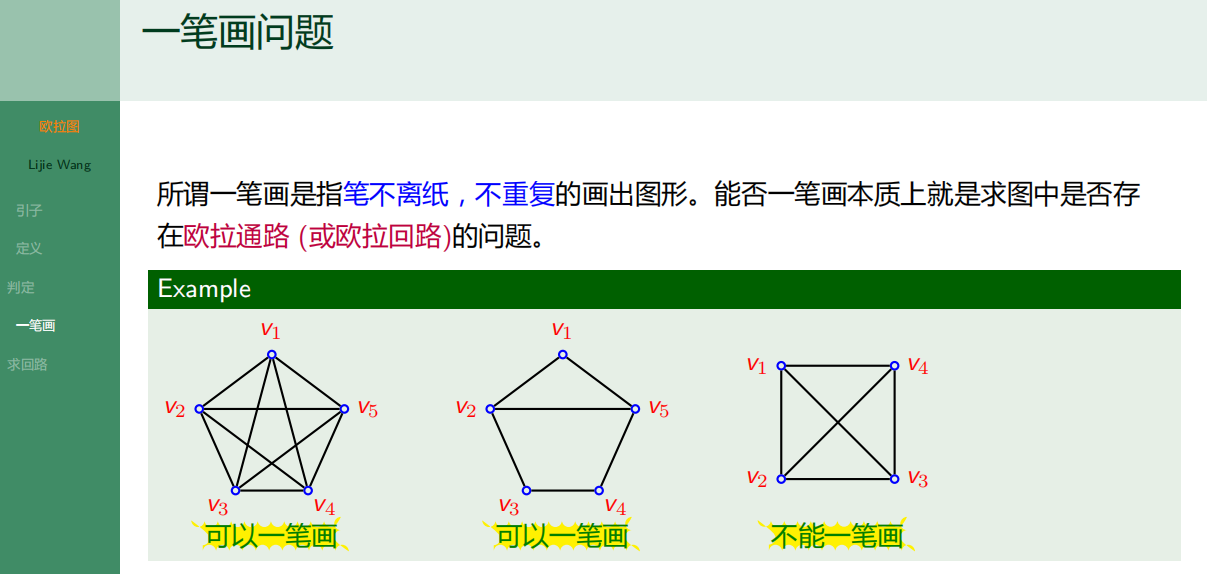
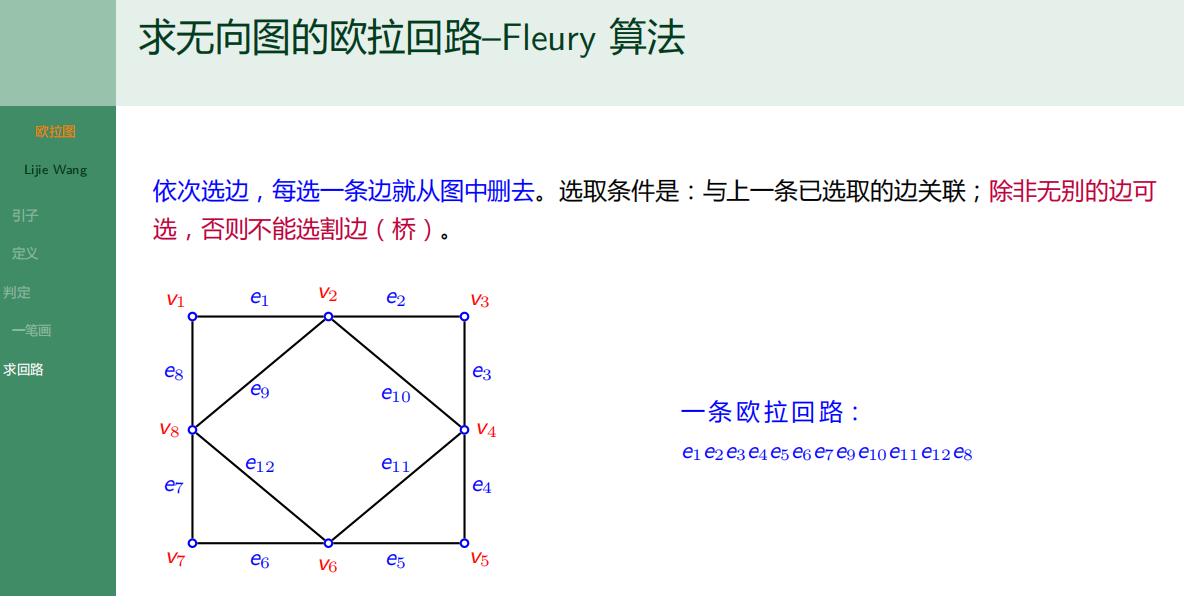
6.1.6 求回路
6.2 哈密顿图
6.2.1 周游世界问题

6.2.2 哈密顿图的定义

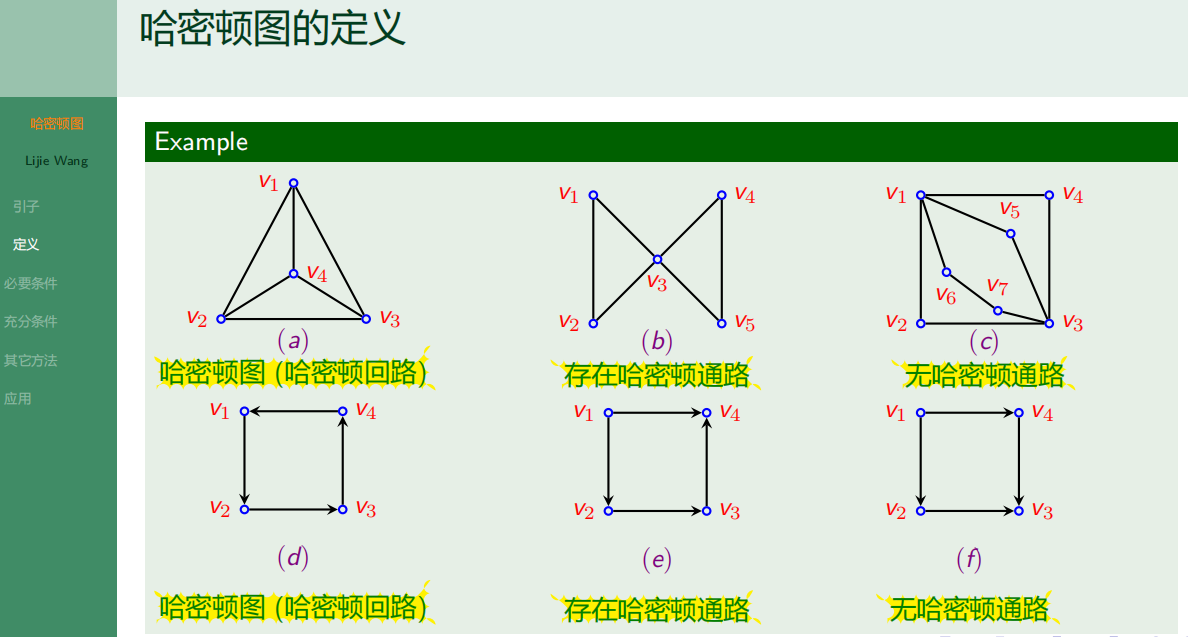
6.2.3 哈密顿图的必要条件

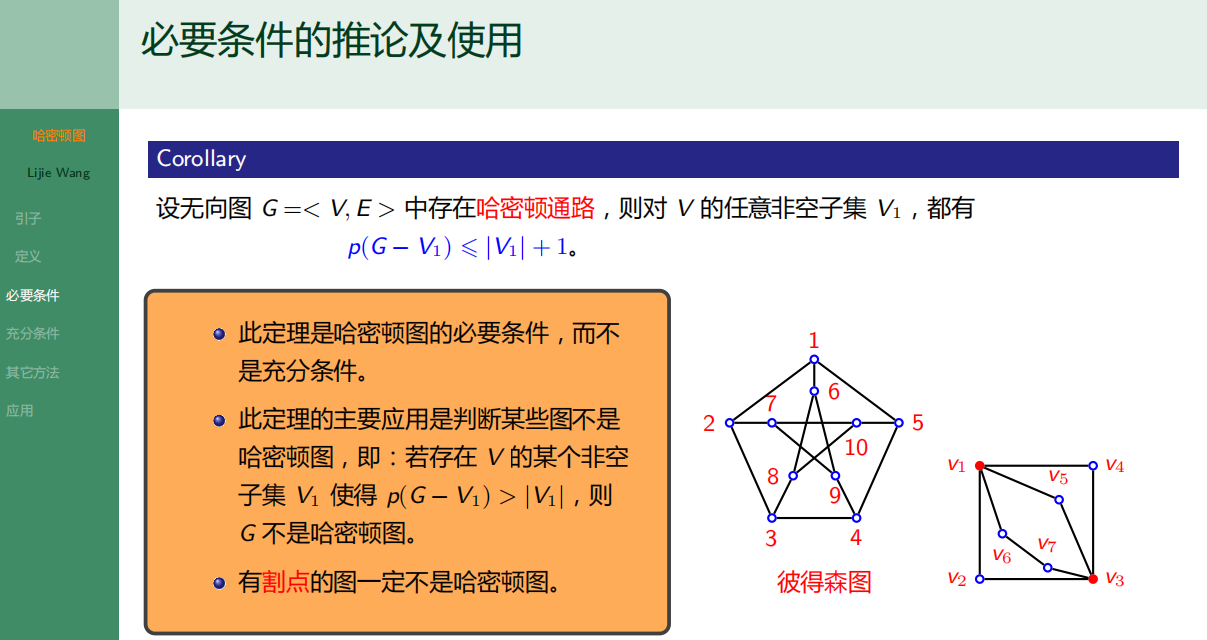
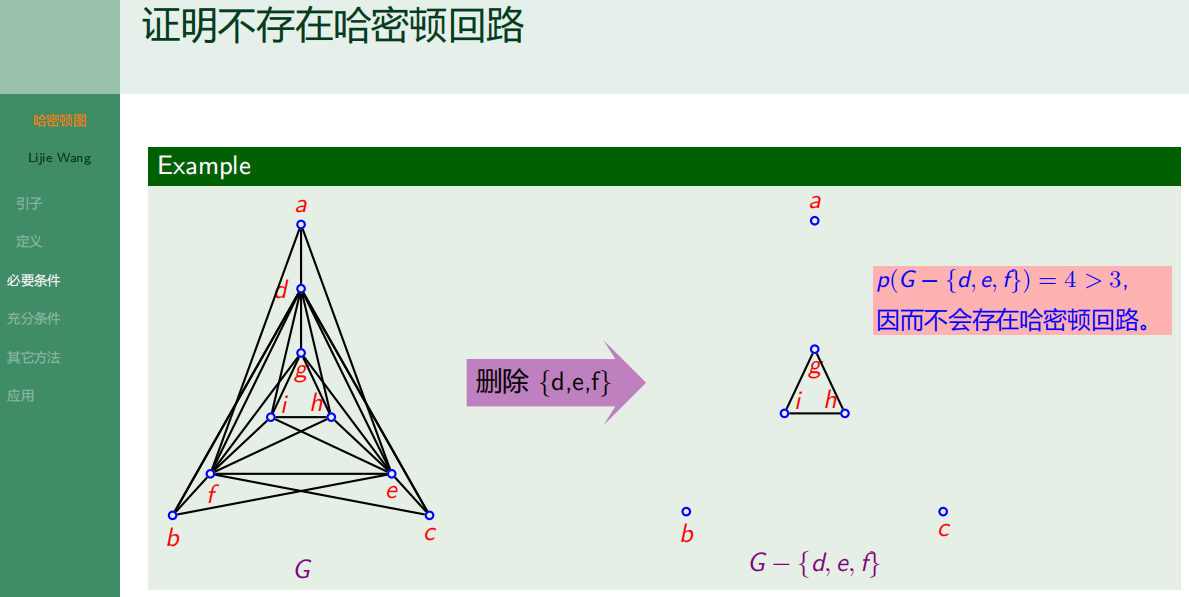
6.2.4 哈密顿图的充分条件
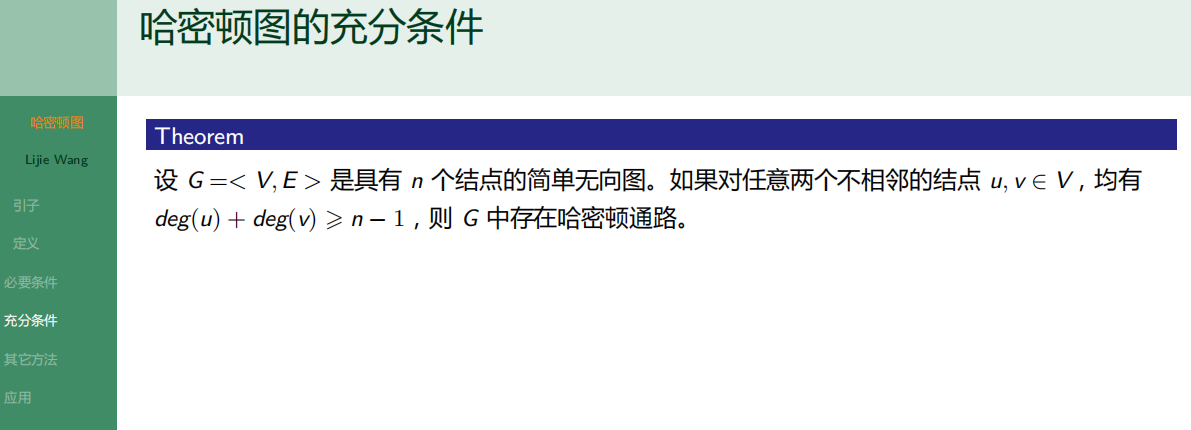


6.2.5 其它方法
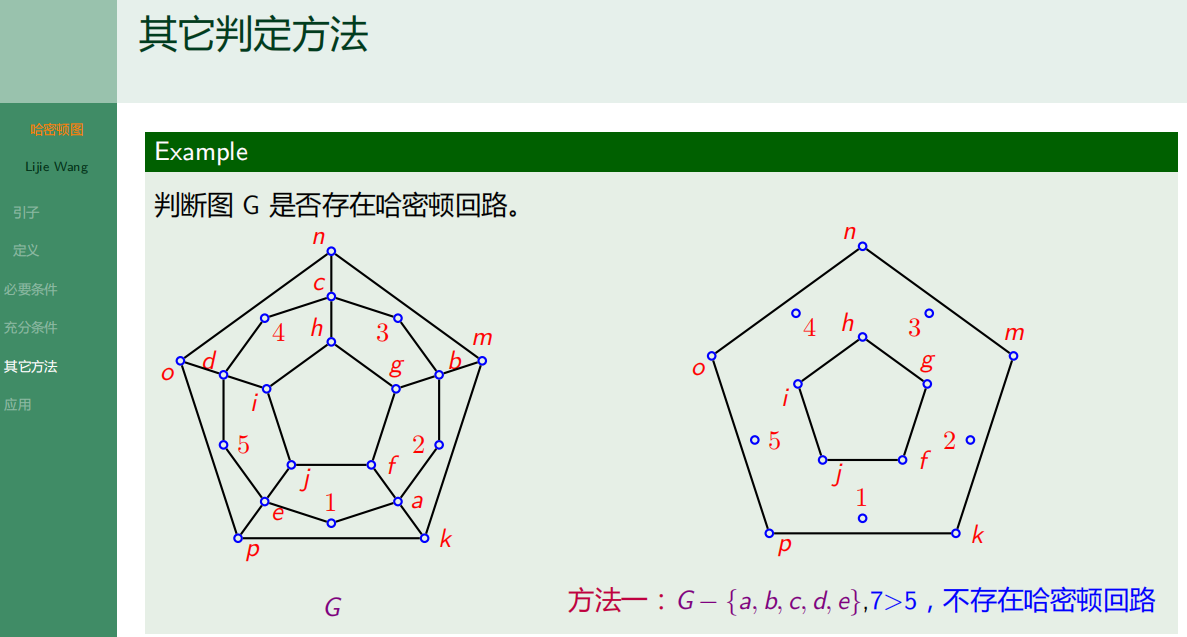
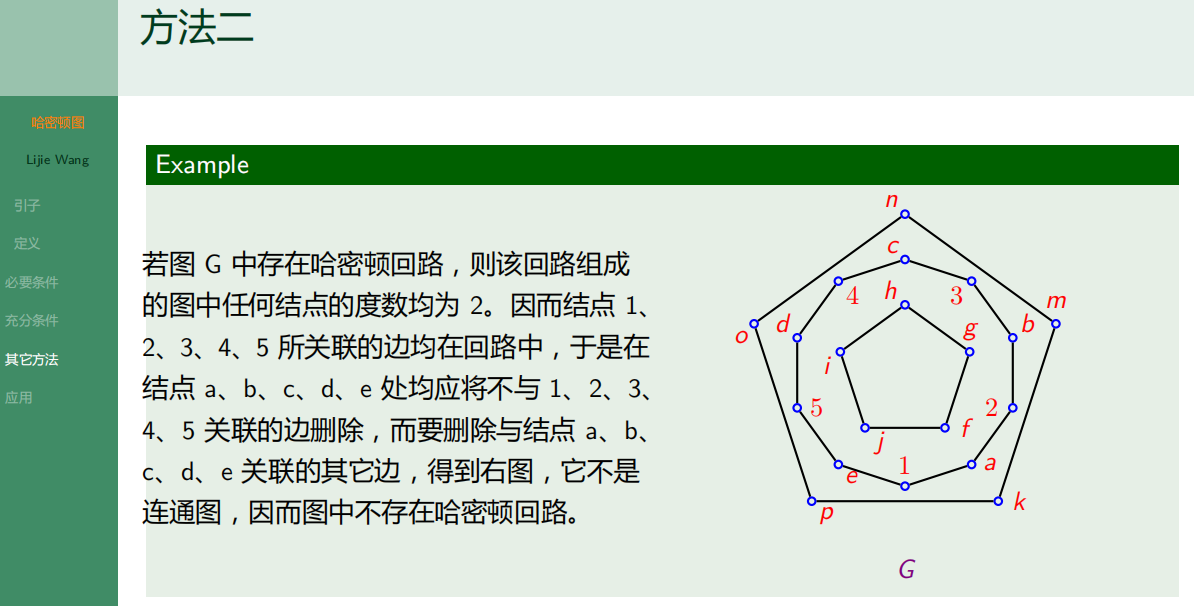
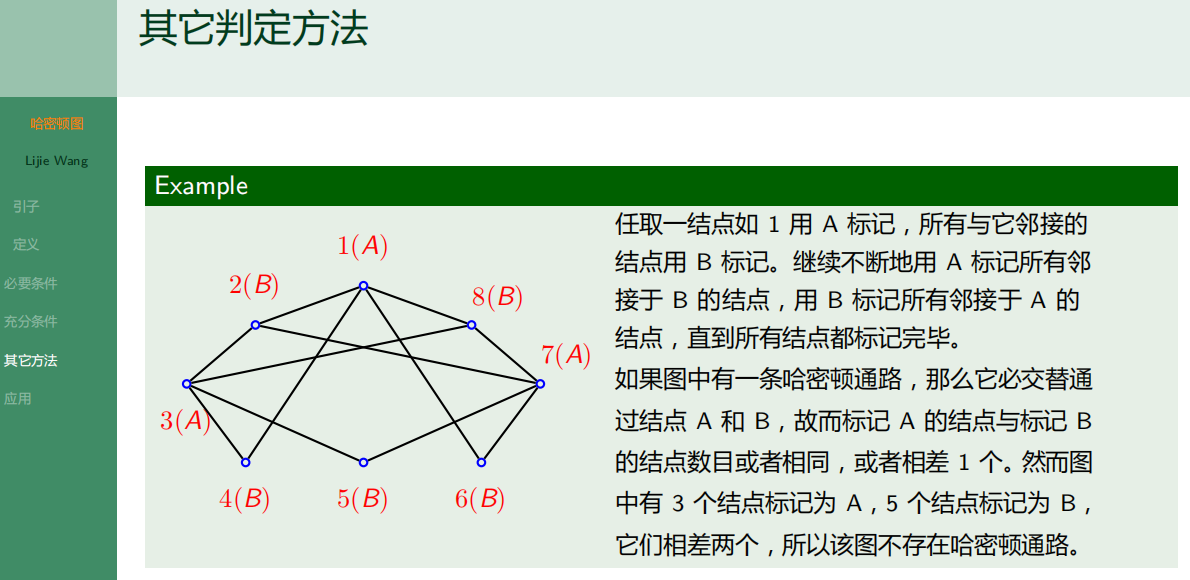
6.2.6 哈密顿图的应用
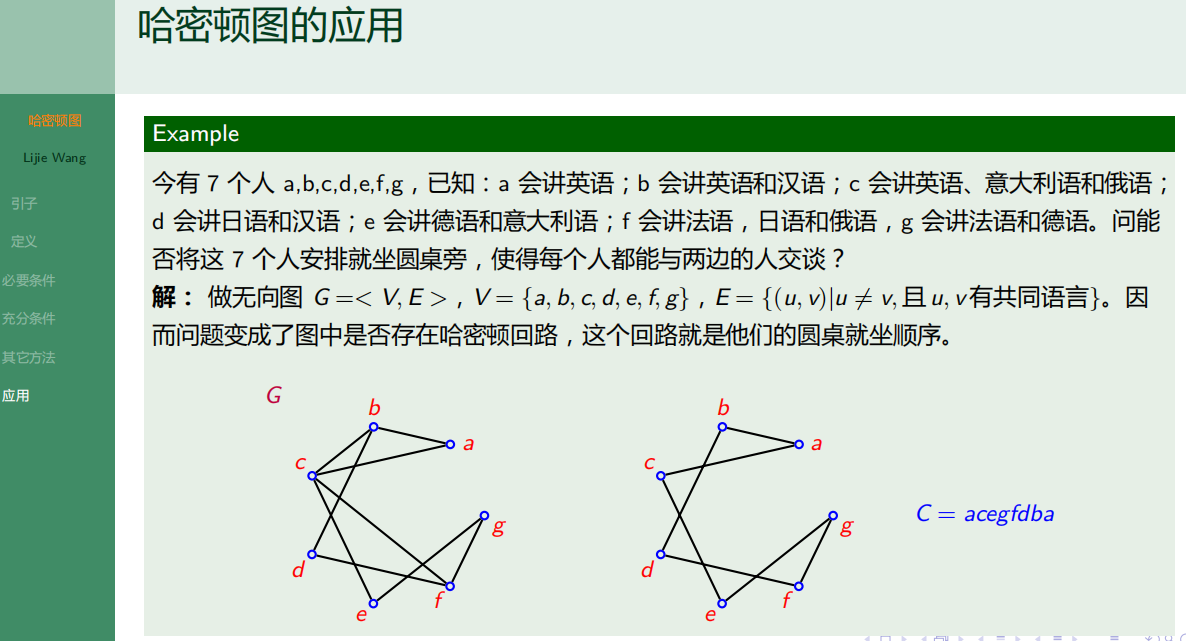
6.3 偶图
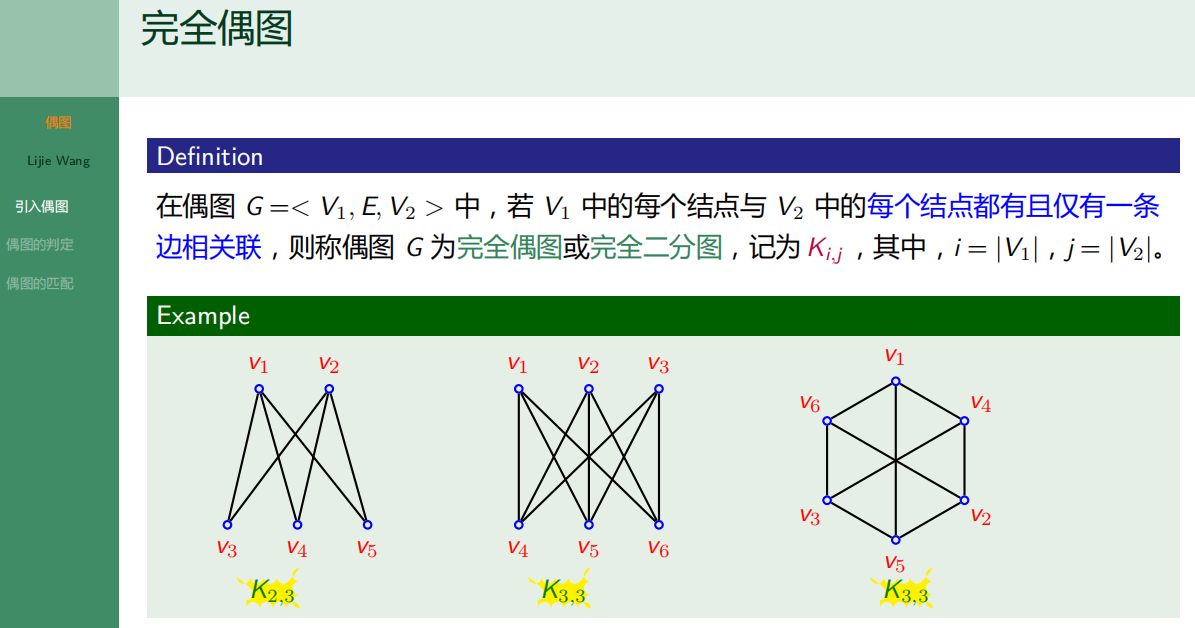
6.3.1 偶图的定义

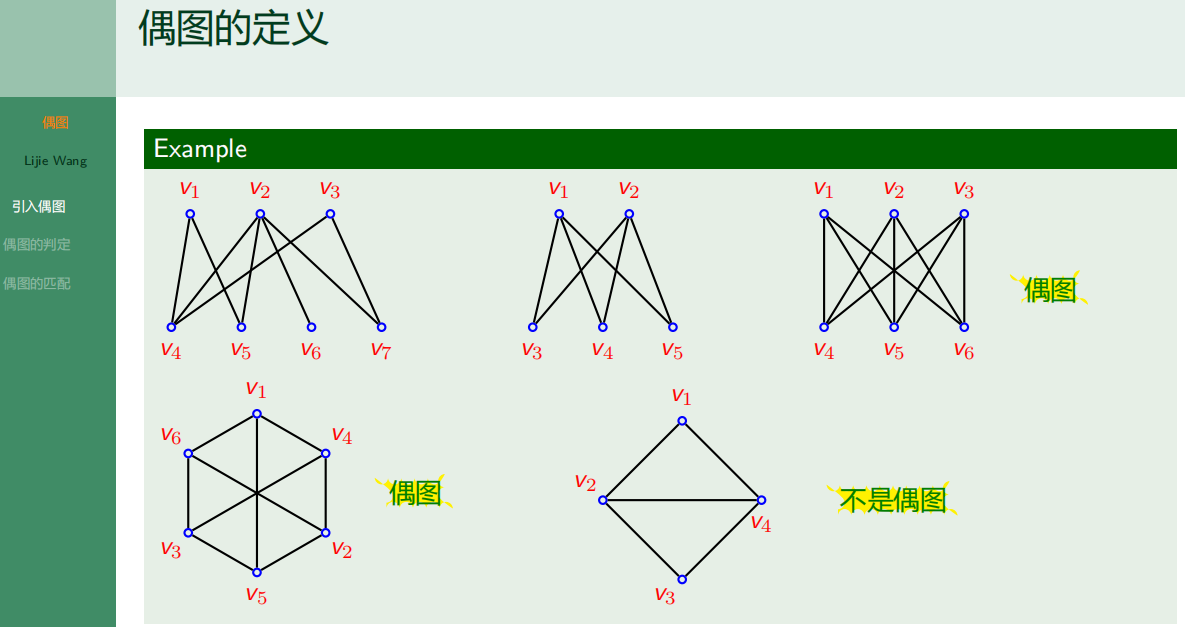
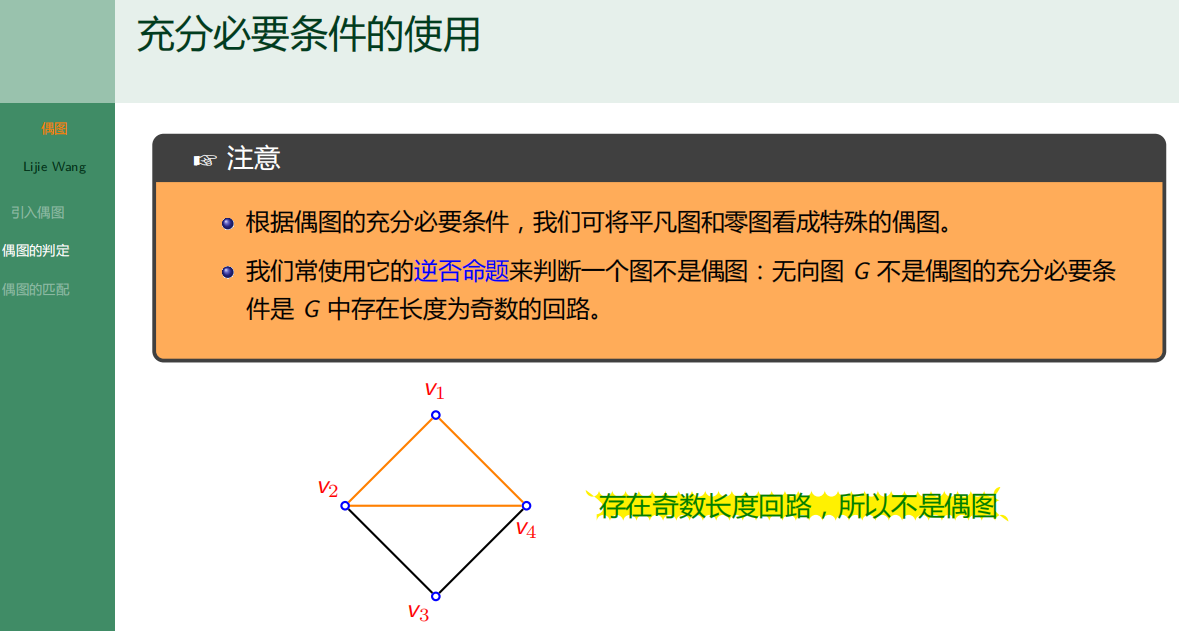
6.3.2 偶图的判定

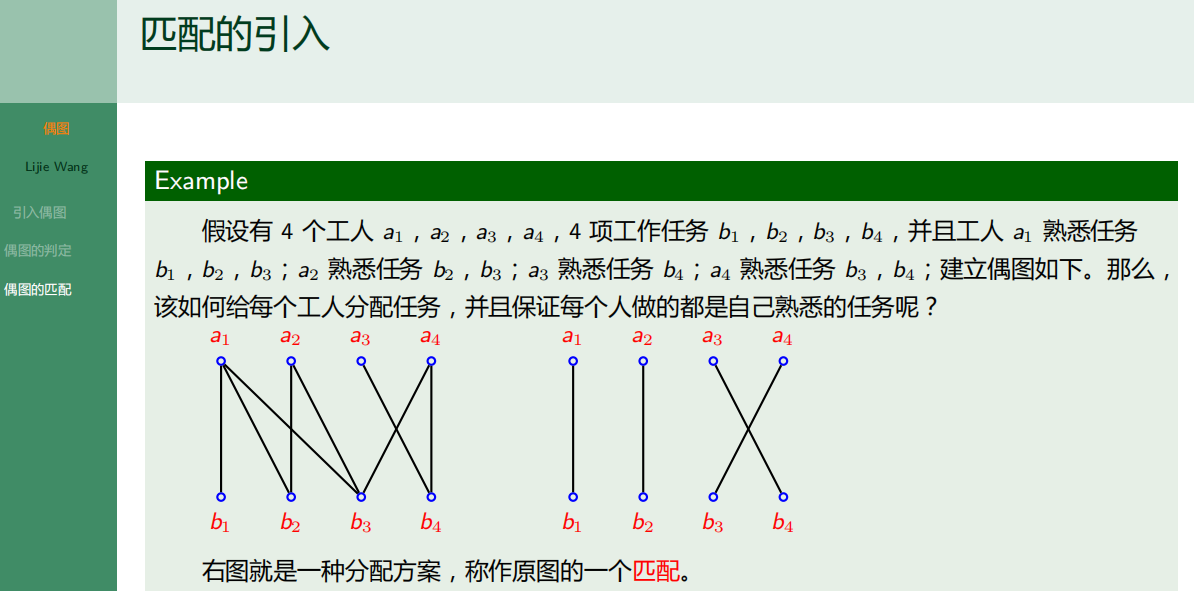
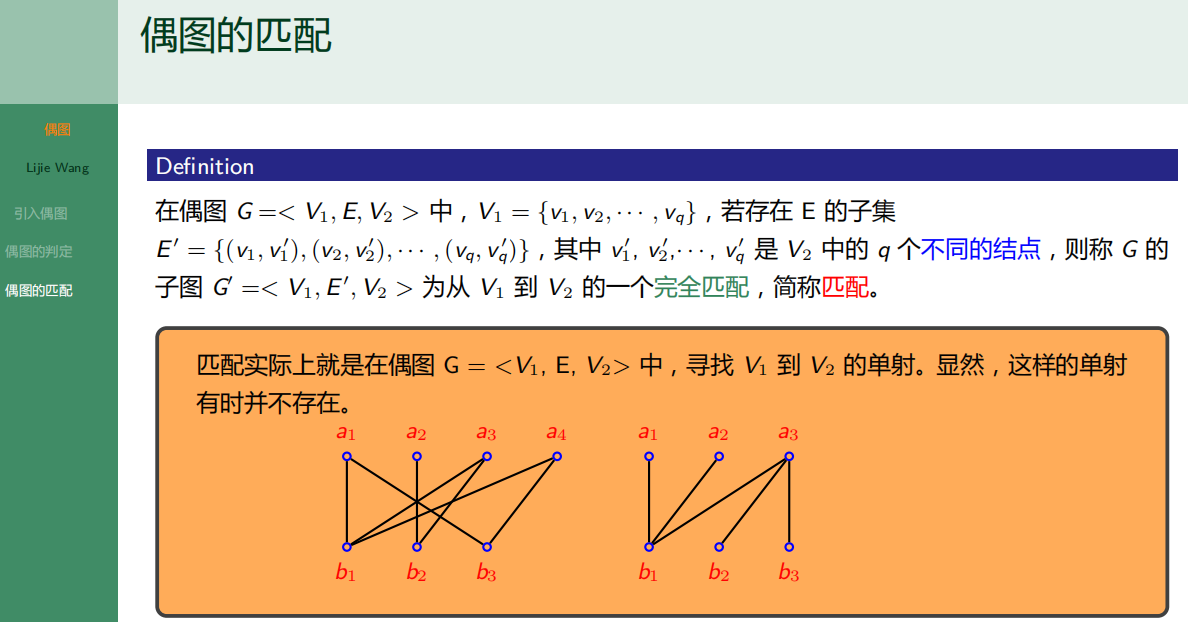
6.3.3 偶图的匹配


6.4 平面图
6.4.1 平面图的定义

6.4.2 平面图的面和边界


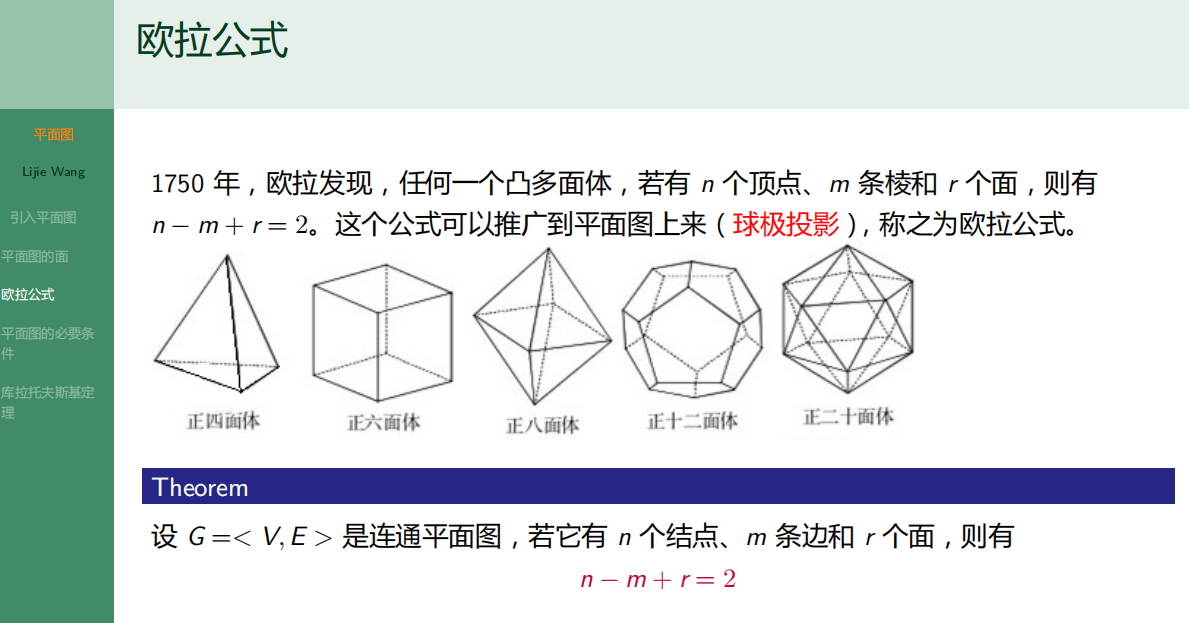
6.4.3 欧拉公式

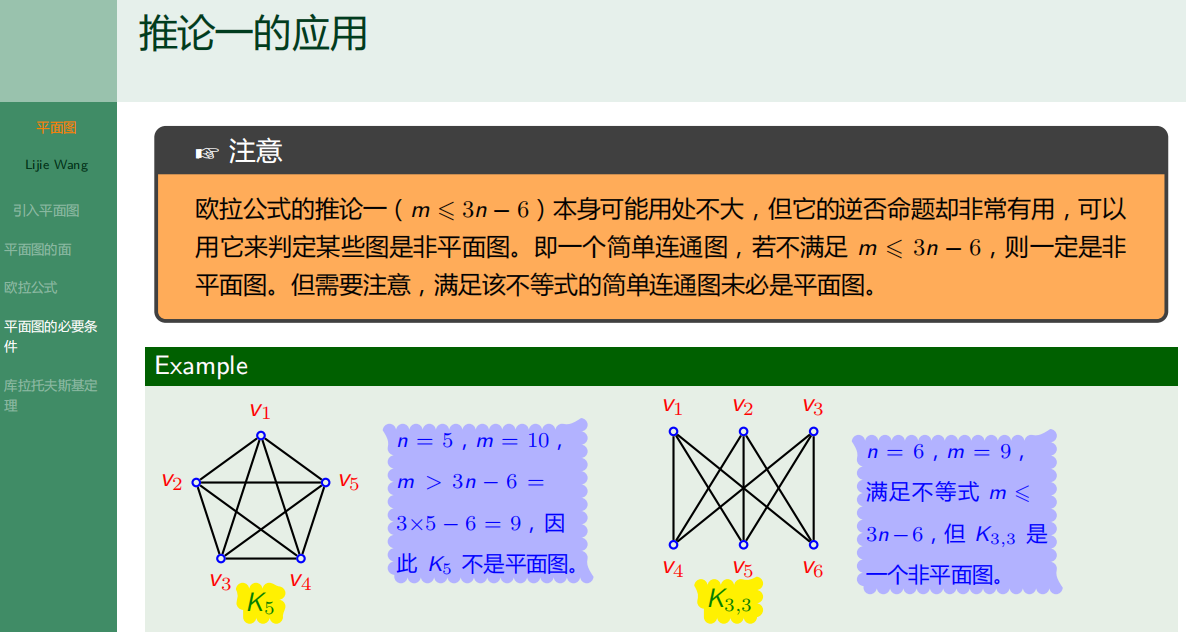
6.4.4 平面图的必要条件


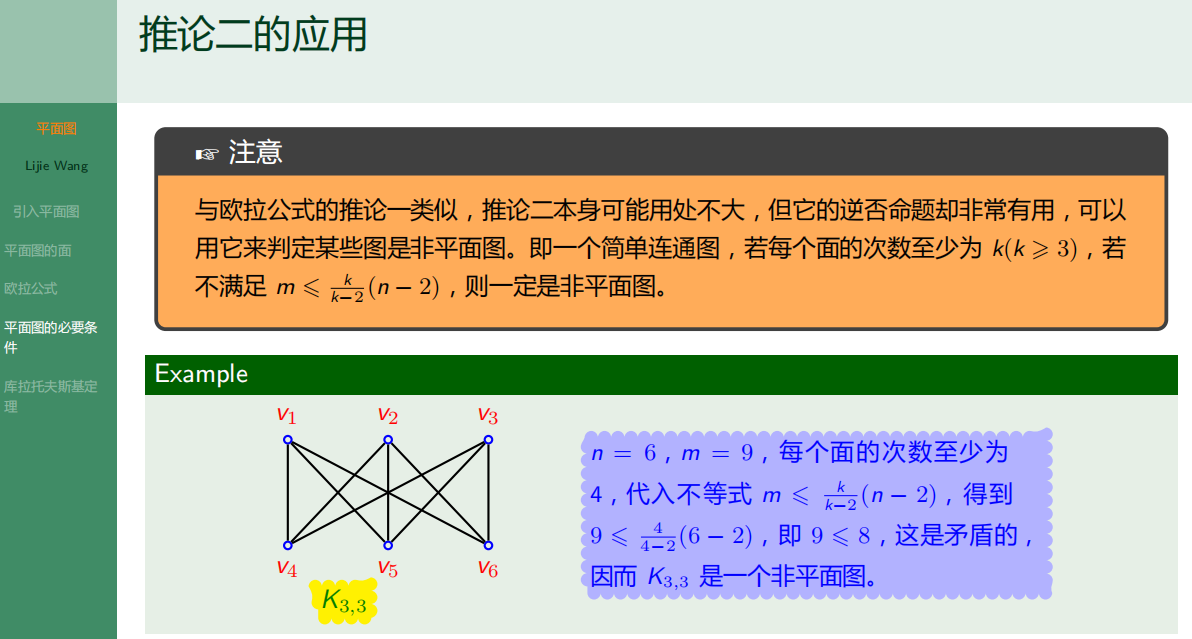
6.4.5 库拉托夫斯基定理
同胚
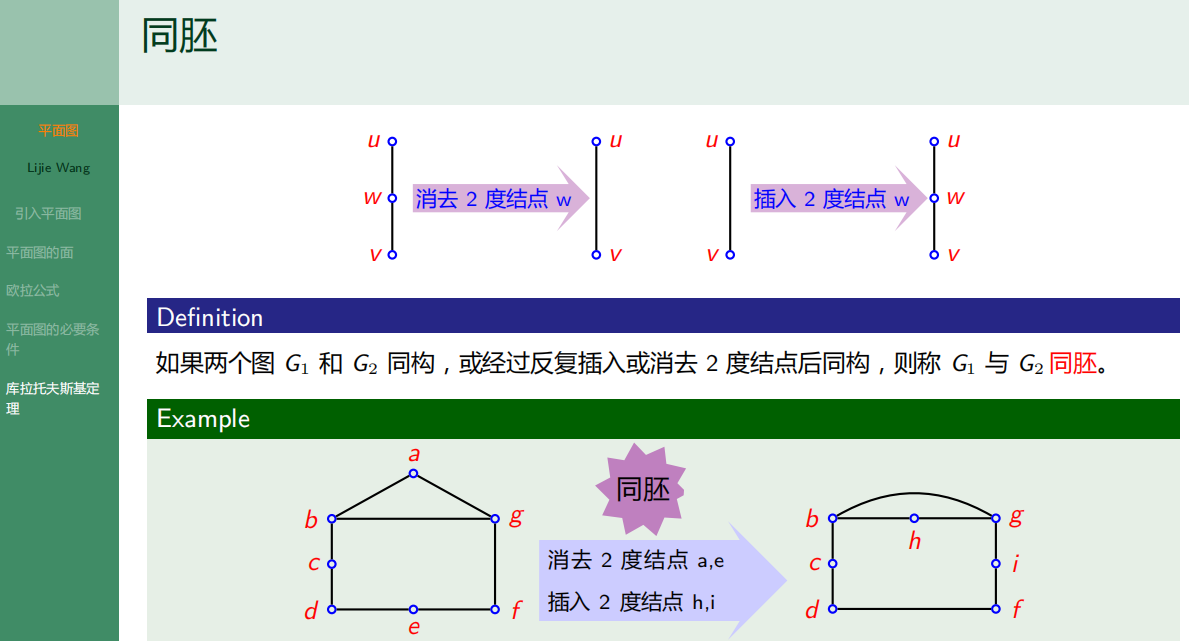
收缩
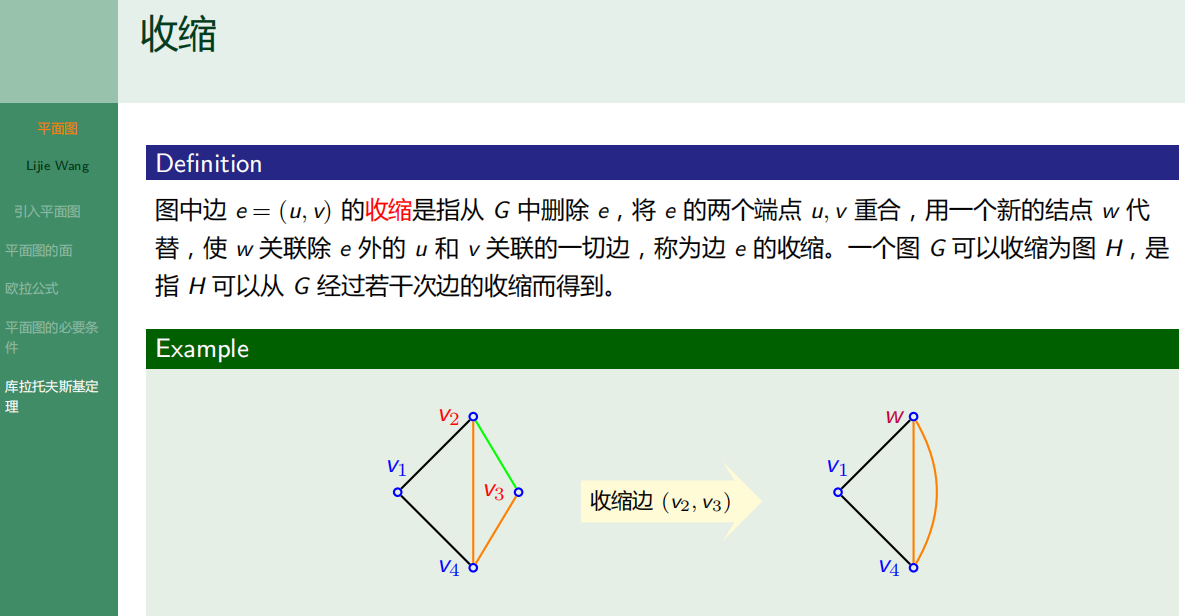
库拉托夫斯基定理
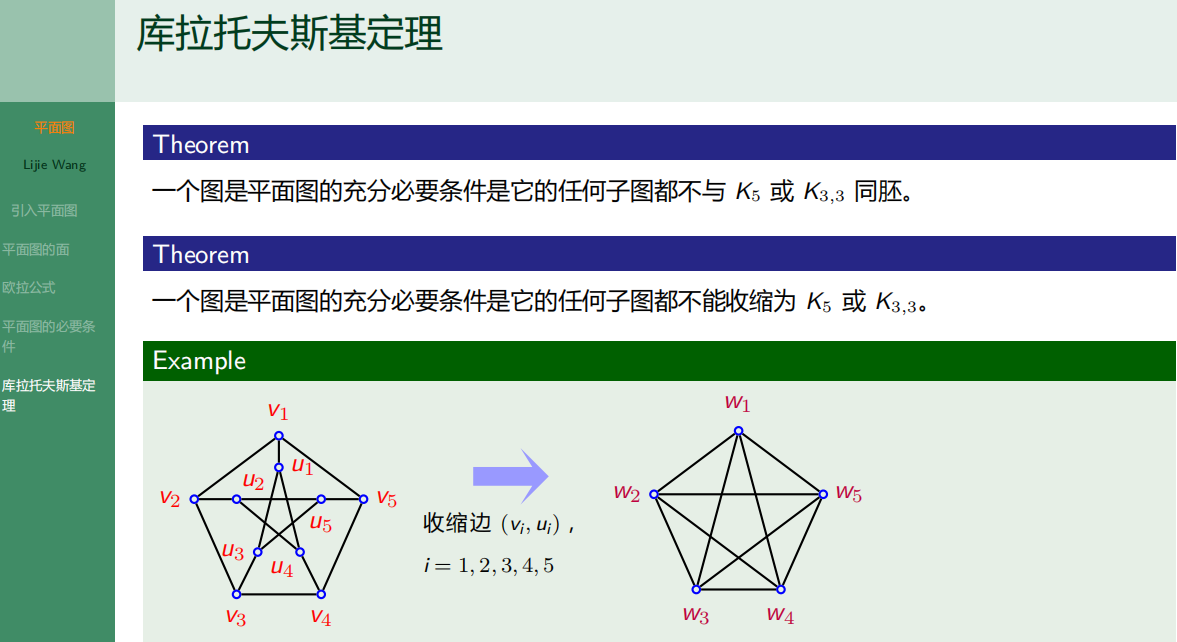
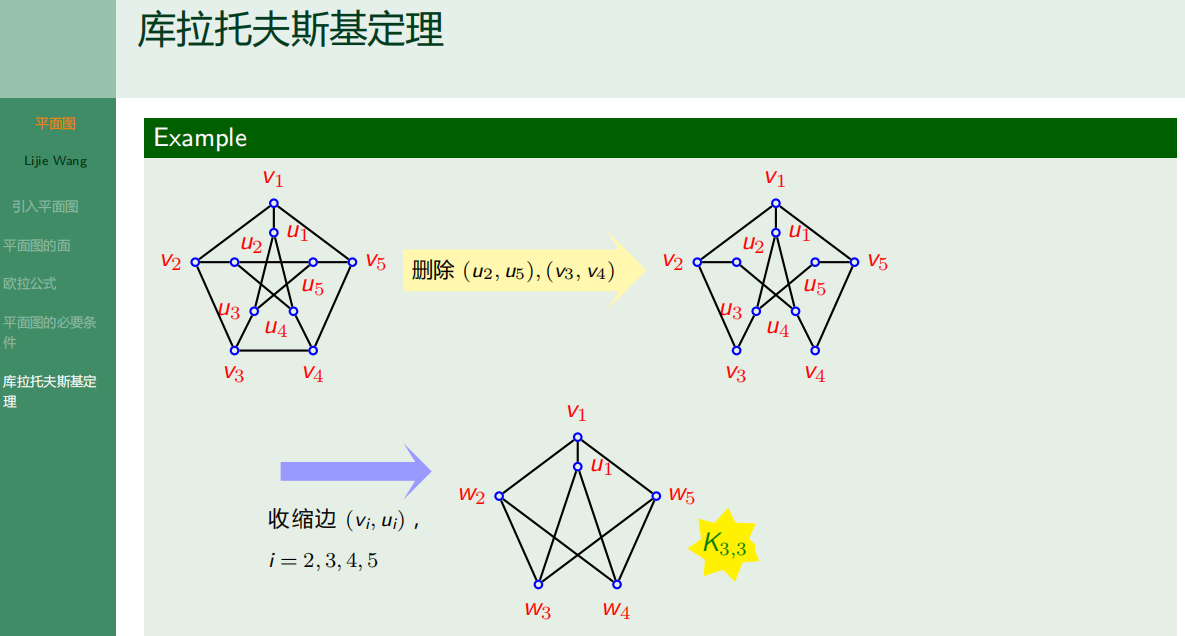
![[WUSTCTF2020]颜值成绩查询(布尔注入)](https://img-blog.csdnimg.cn/f3db04f98a9f4fdebdf0c3d8e7cd800f.png)