函数知识点总结
- 函数知识点总结
- 一、平面直角坐标系中点的坐标
- 1. 各象限内
- 2. 坐标轴上
- 3. 各象限角平分线上
- 4. 与坐标轴平行的直线上的点
- 5. 点到坐标轴及原点的距离
- 6. 平面上两点距离
- 一、平面直角坐标系中点的坐标
一、平面直角坐标系中点的坐标
1. 各象限内
| 象限 | x , y x,\,y x,y 的关系 |
|---|---|
| 第一象限 | x > 0 , y > 0 x>0,\,y>0 x>0,y>0 |
| 第二象限 | x < 0 , y > 0 x<0,\,y>0 x<0,y>0 |
| 第三象限 | x < 0 , y > 0 x<0,\,y>0 x<0,y>0 |
| 第四象限 | x > 0 , y > 0 x>0,\,y>0 x>0,y>0 |
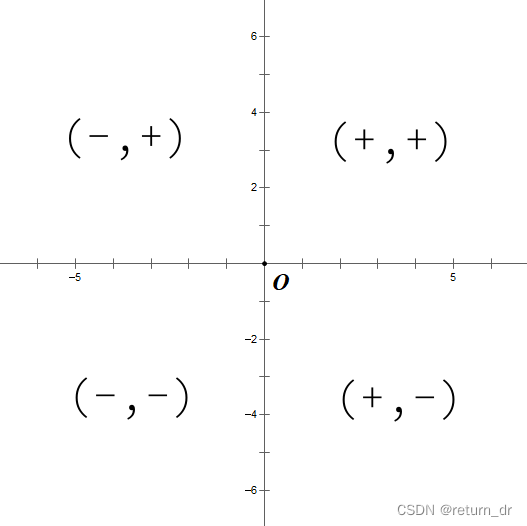
注:坐标轴上的点不属于任何象限。
2. 坐标轴上
点在 x x x 轴上: y = 0 y=0 y=0;点在 y y y 轴上: x = 0 x=0 x=0;
原点 O O O 的坐标: ( 0 , 0 ) (0,\,0) (0,0) 。
3. 各象限角平分线上
第一、三象限角平分线上:
y
=
x
y=x
y=x;
第二、四象限角平分线上:
y
=
−
x
y=-x
y=−x。
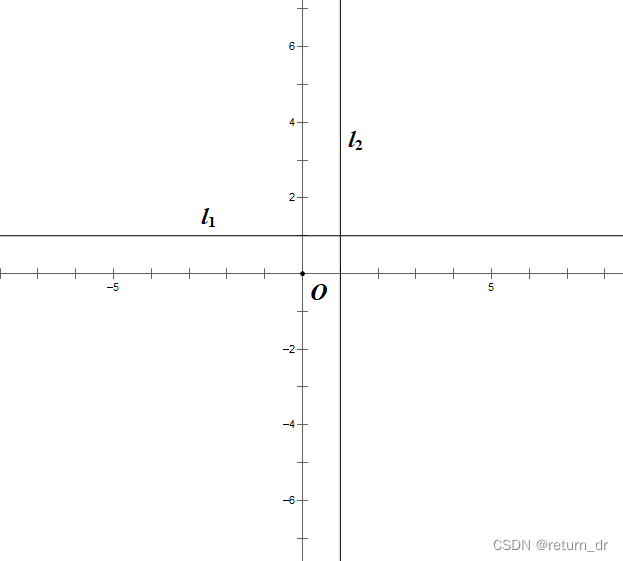
4. 与坐标轴平行的直线上的点
平行于
x
x
x 轴的直线
l
1
l_1
l1 上的点的纵坐标相等;
平行于
y
y
y 轴的直线
l
2
l_2
l2 上的点的横坐标相等。
5. 点到坐标轴及原点的距离
点 P ( x , y ) P(x,\,y) P(x,y) 到 x x x 轴的距离为 ∣ b ∣ |b| ∣b∣,到 y y y 轴的距离为 ∣ a ∣ |a| ∣a∣,到原点 O O O 的距离为 a 2 + b 2 \sqrt{a^2+b^2} a2+b2.
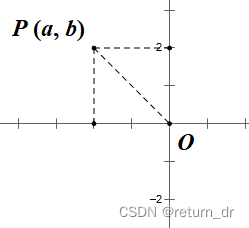
6. 平面上两点距离
如图,点 P 1 ( a 1 , b 1 ) , P 2 ( a 2 , b 2 ) P_1(a_1,\,b_1),\,P_2(a_2,\,b_2) P1(a1,b1),P2(a2,b2) 两点之间的距离为 P 1 P 2 = ( a 1 − a 2 ) 2 + ( b 1 − b 2 ) 2 P_1P_2=\sqrt{(a_1-a_2)^2+(b_1-b_2)^2} P1P2=(a1−a2)2+(b1−b2)2。
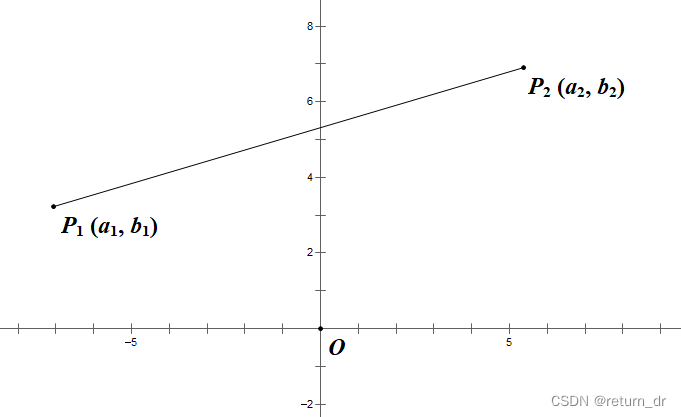
7. 点到直线的距离公式
如图,点 P ( x , y ) P(x,\,y) P(x,y) 到直线 A x + B y + C = 0 Ax+By+C=0 Ax+By+C=0 的距离为 d = ∣ A x + B y + C ∣ A 2 + B 2 d=\dfrac{|Ax+By+C|}{\sqrt{A^2+B^2}} d=A2+B2∣Ax+By+C∣。
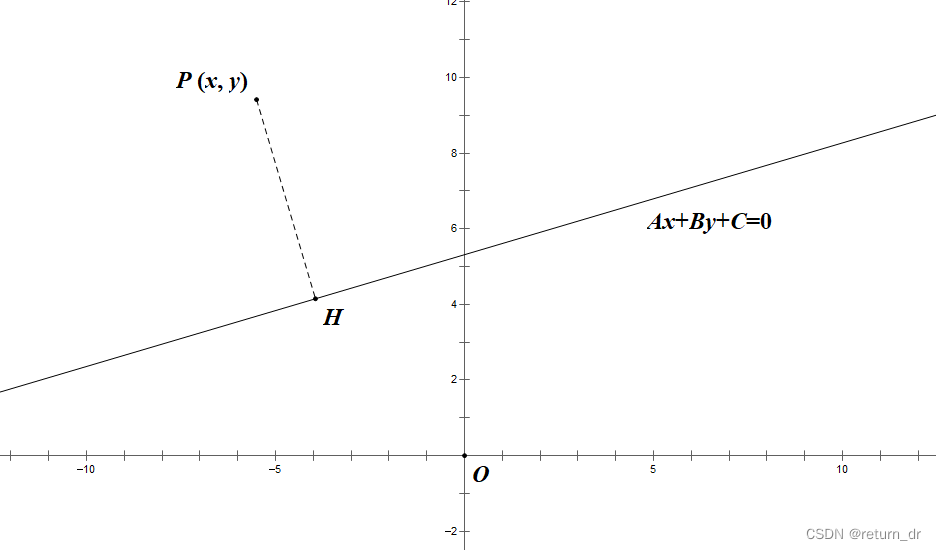
8. 点的对称
{ P 1 ( a , b ) → x P 2 ( a , − b ) P 1 ( a , b ) → y P 2 ( − a , b ) P 1 ( a , b ) → O ( 0 , 0 ) P 2 ( − a , − b ) \begin{cases}P_1\,(a,\,b)\xrightarrow{x}P_2\,(a,\,-b)\\ P_1\,(a,\,b)\xrightarrow{y}P_2\,(-a,\,b) \\ P_1\,(a,\,b)\xrightarrow{O\,(0,\,0)}P_2\,(-a,\,-b)\end{cases} ⎩ ⎨ ⎧P1(a,b)xP2(a,−b)P1(a,b)yP2(−a,b)P1(a,b)O(0,0)P2(−a,−b)
9. 点的平移
| 平移方式 ( a > 0 , b > 0 ) (a>0,\,b>0) (a>0,b>0) | 平移后点 P ′ P' P′ 的坐标 |
|---|---|
| 向左平移 a a a 个单位 | ( x − a , y ) (x-a,\,y) (x−a,y) |
| 向右平移 a a a 个单位 | ( x + a , y ) (x+a,\,y) (x+a,y) |
| 向上平移 b b b 个单位 | ( x , y + b ) (x,\,y+b) (x,y+b) |
| 向下平移 b b b 个单位 | ( x , y − b ) (x,\,y-b) (x,y−b) |
口诀:左右平移,左加右减;上下平移,上加下减。
二、函数的图像与性质
1. 概念
一般地,如果在一个变化过程中有两个变量 x x x 和 y y y,并且对于变量 x x x 的每一个值,变量 y y y 都有唯一的值与它对应,那么我们称 y y y 是 x x x 的函数,其中 x x x 是自变量, y y y 是因变量。
2. 表示
列表法、关系式法、图像法