各位uu们你们好呀，今天小雅兰要学习的内容仍然是高等数学，是为：极限存在准则 两个重要极限。那现在就让我们一起进入高等数学的世界吧
引例
夹逼准则
准则Ⅰ 数列的夹逼准则
准则Ⅰ’ 函数的夹逼准则
重要极限Ⅰ
准则Ⅱ 单调有界数列必有极限
重要极限Ⅱ
引例 化繁为简
这是一个首项为1/2，公比为1/2的等比数列，等比数列的和用等比数列前n项和的公式即可求出。
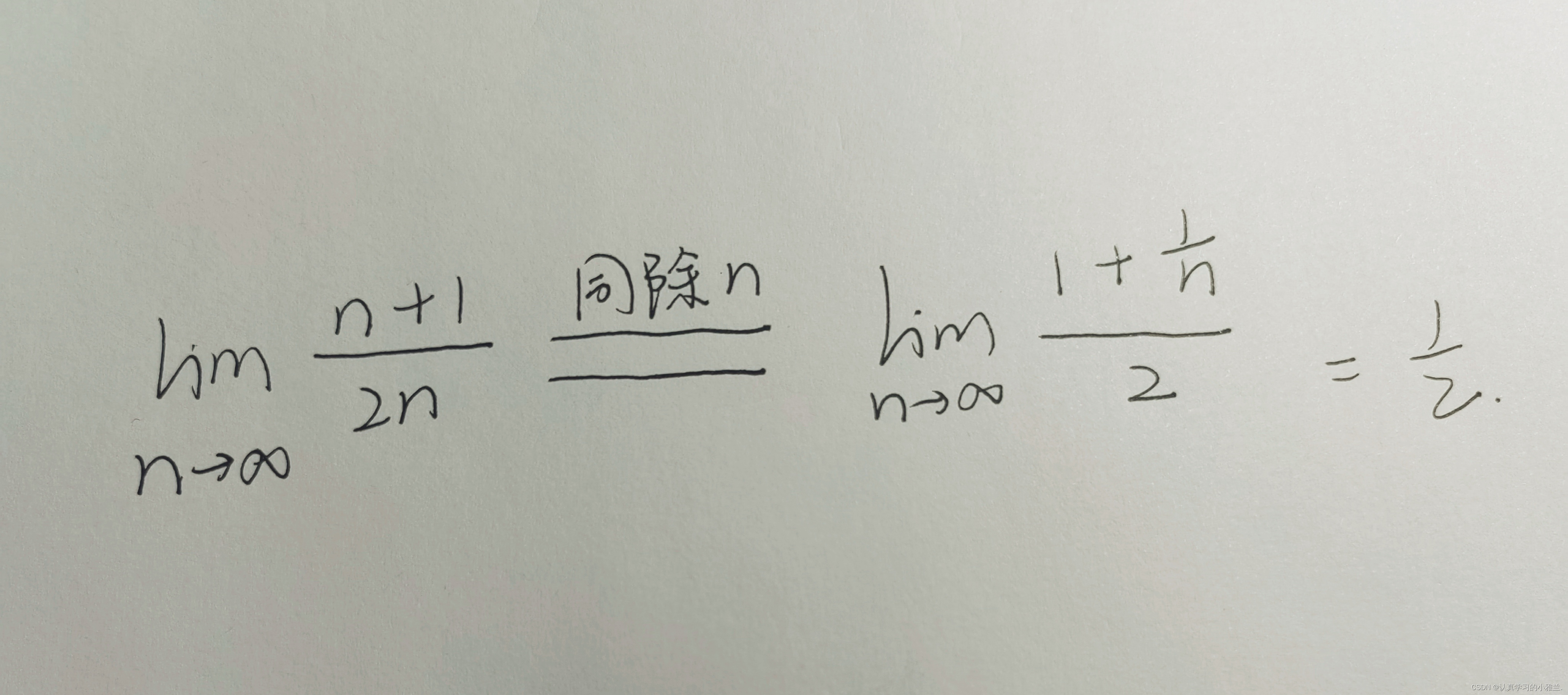
此引例的分子是一个首项为1，公差为1的等差数列，等差数列前n项和也是直接运用等差数列前n项和的公式求解即可。
我们来回顾一下高中学习过的内容，就是等差数列和等比数列
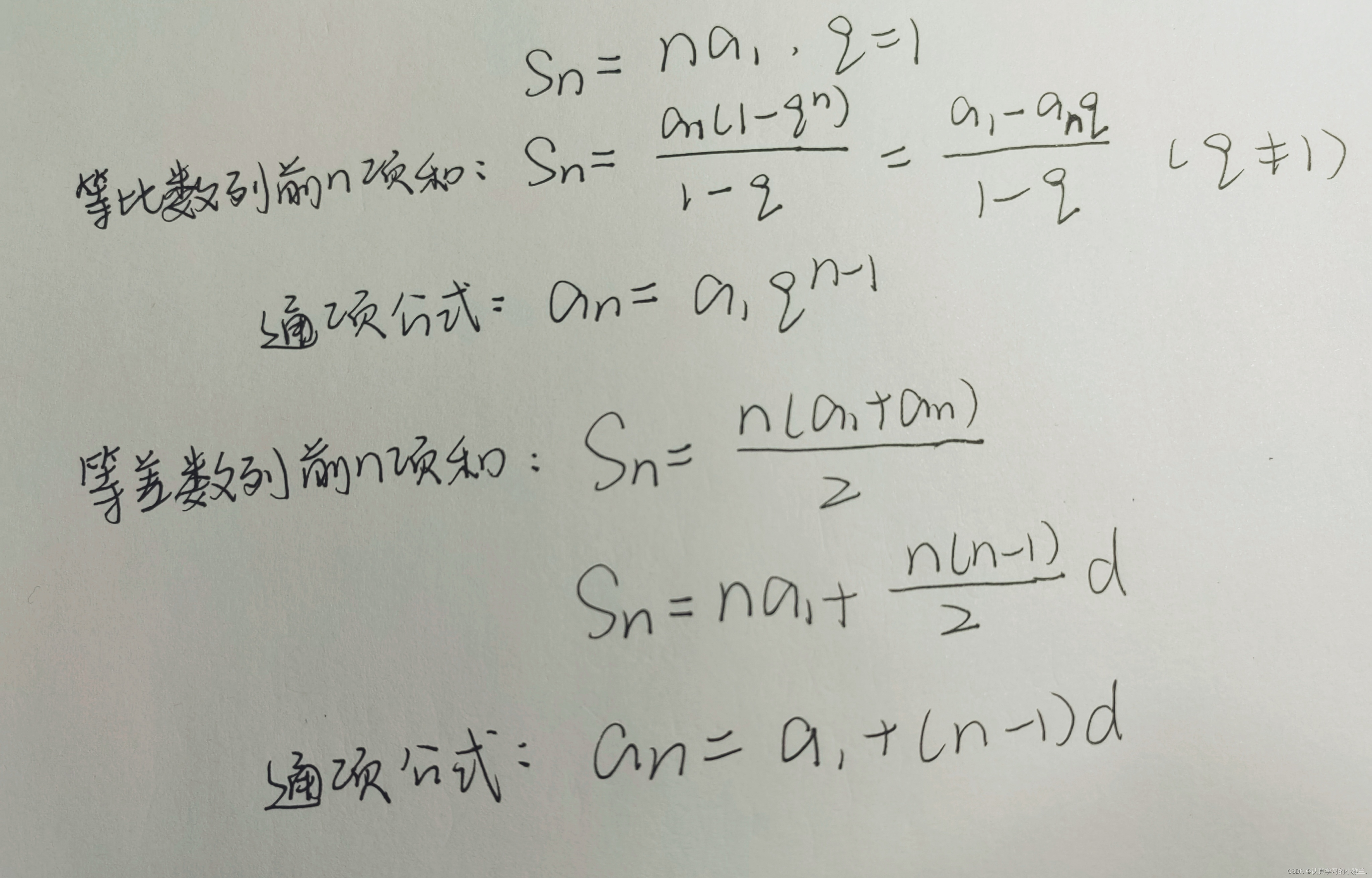
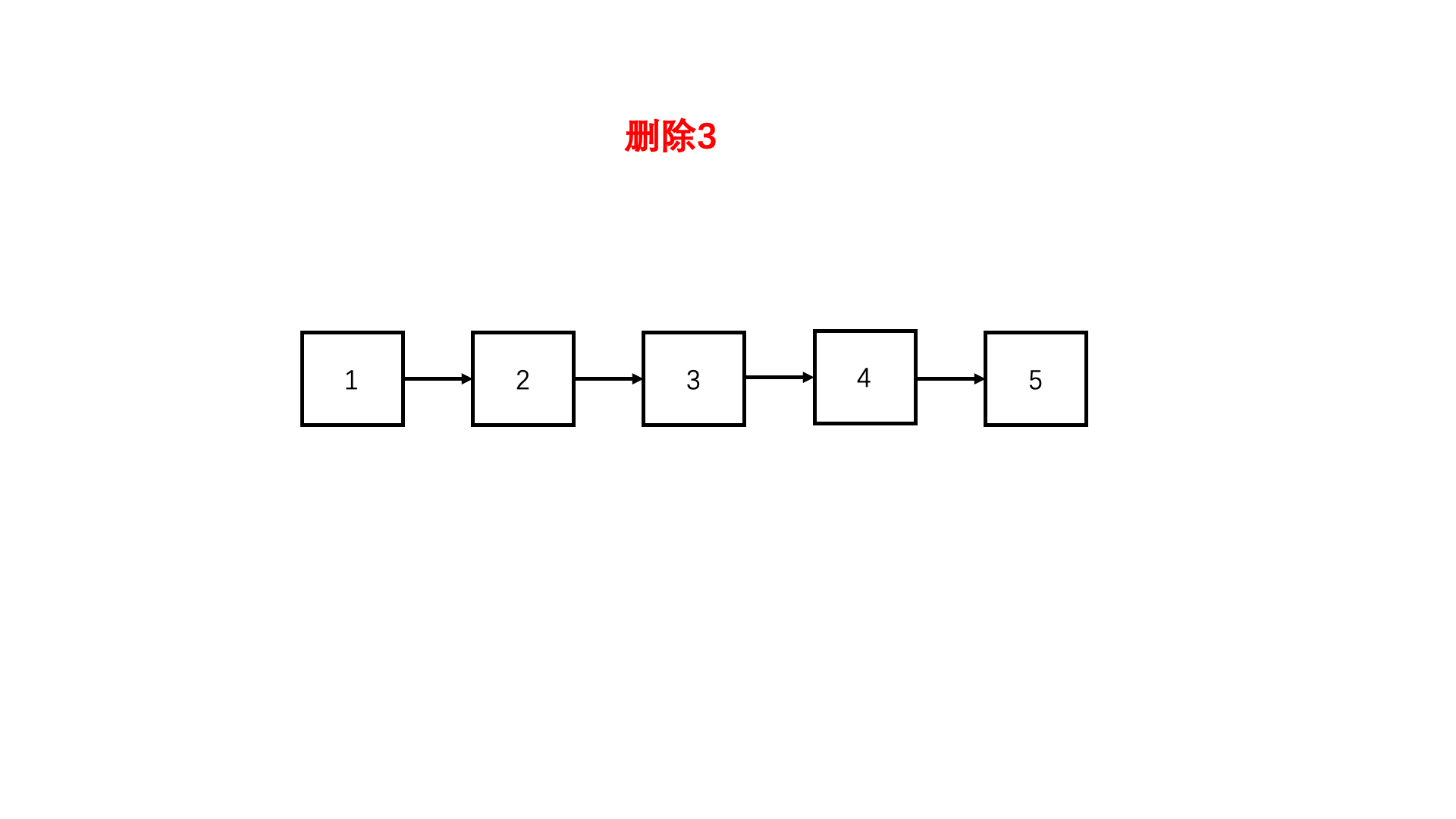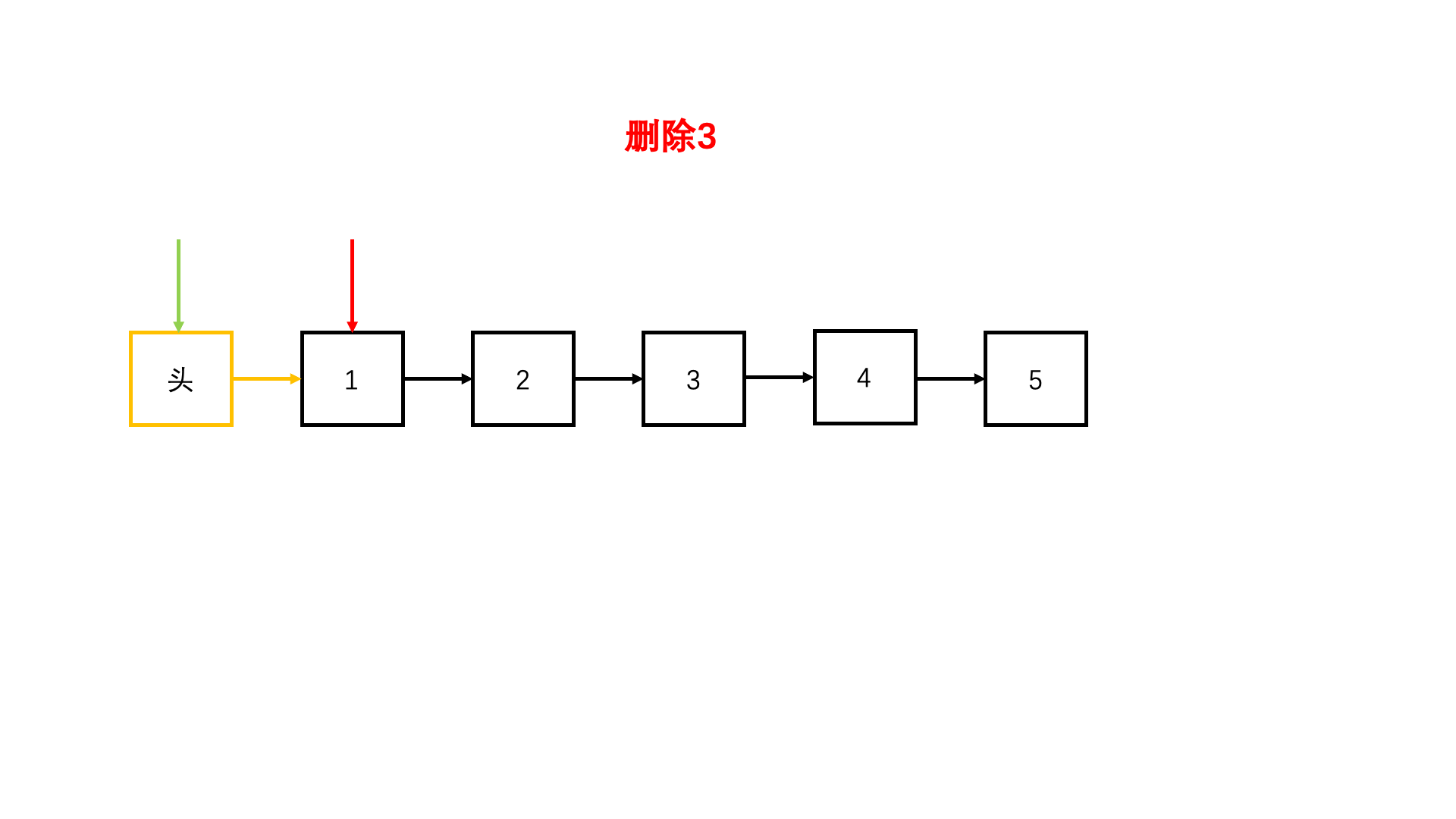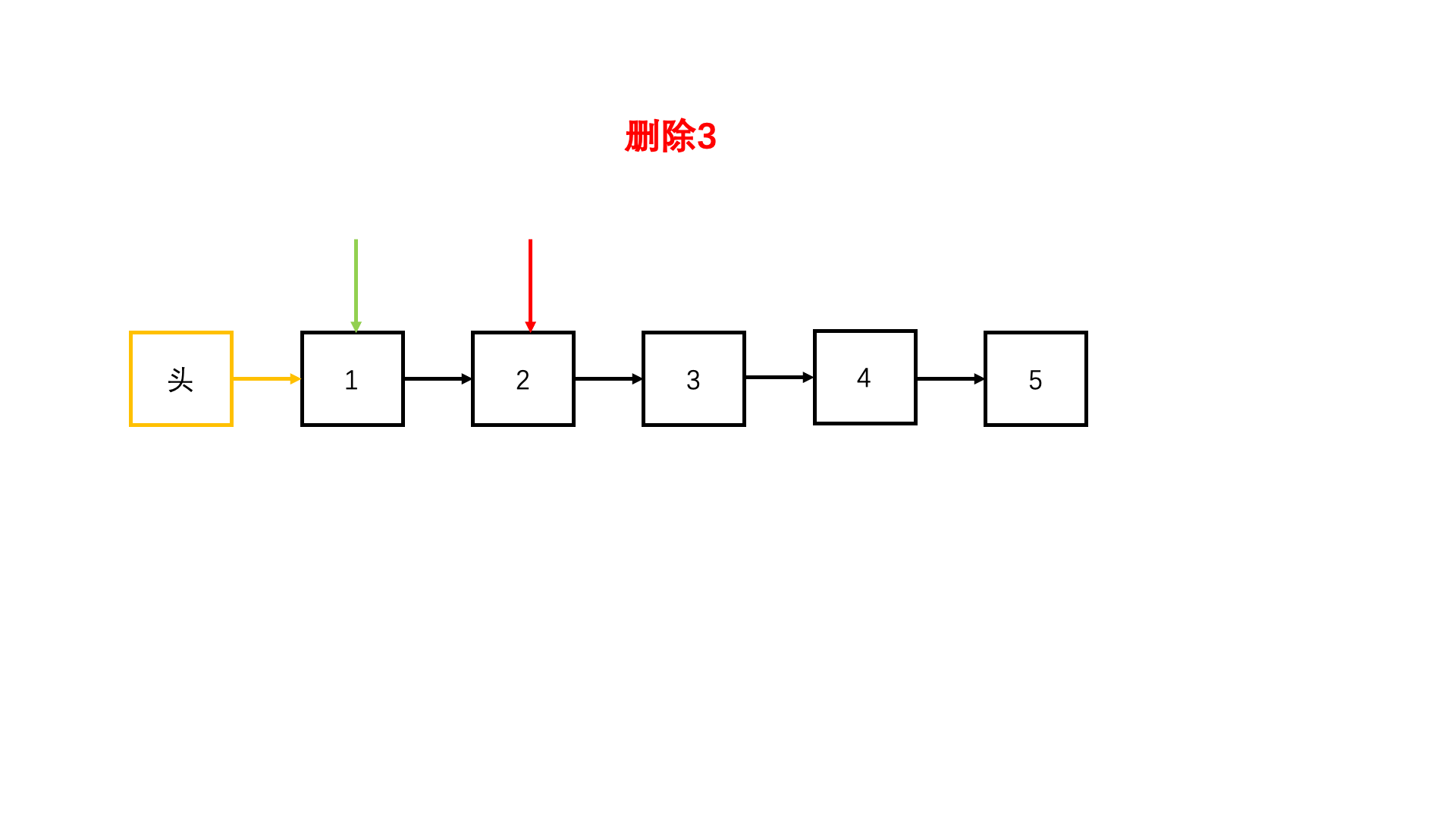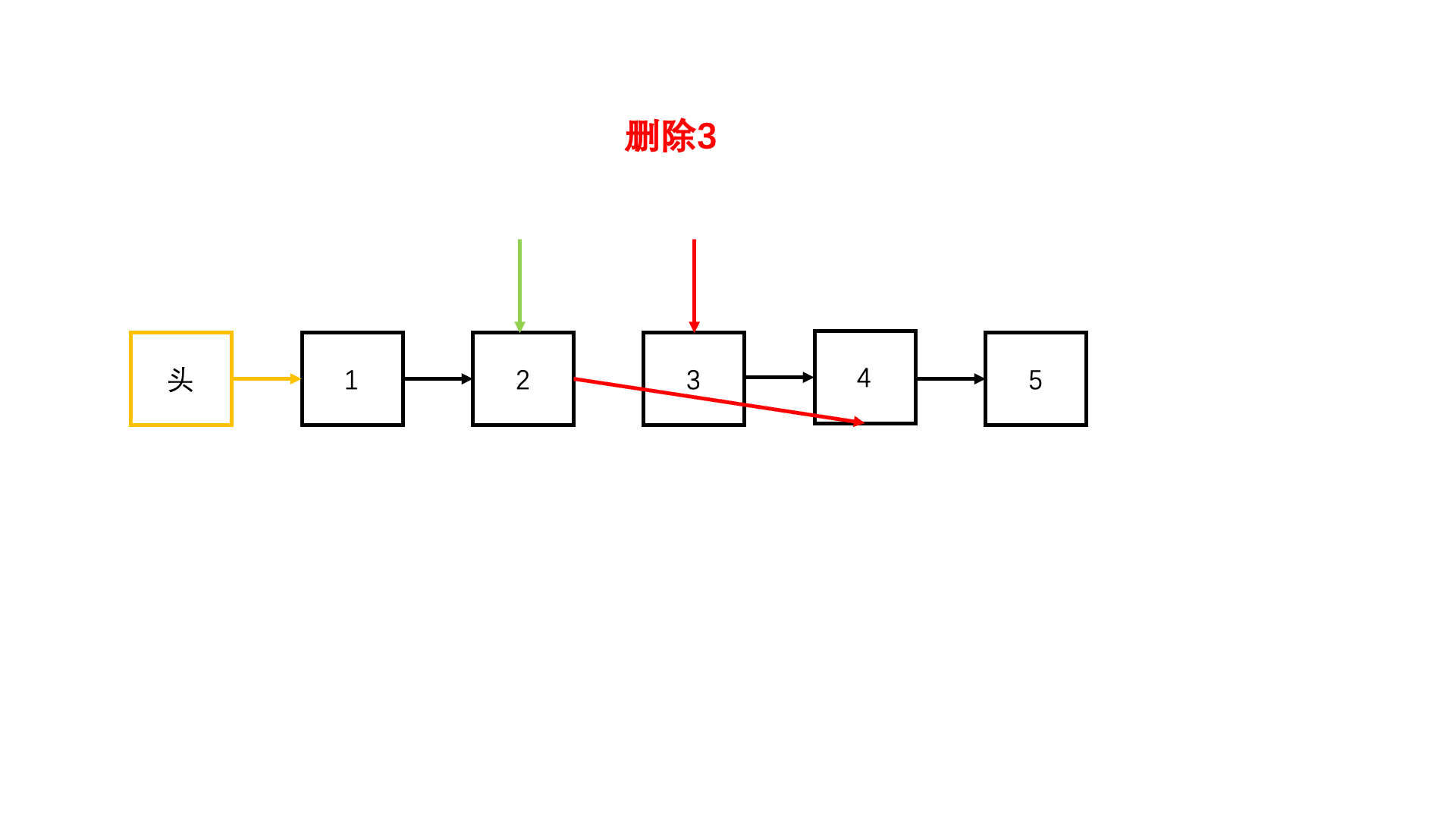
大家来看第三个题目，我们发现：根据已有的知识，要解出这个题目，是非常困难的，而且极易犯错误，所以我们势必得学习一些新方法
这就是我们本节课的内容了
一、夹逼准则
准则Ⅰ 数列的夹逼准则
下面，我们来证明一下准则Ⅰ
下面对准则Ⅰ说明几点
等会儿看完几个例题之后再来说明一点 下面 我们来看看我们先之前说的那个对于没学夹逼准则之前很难解决的那个例题
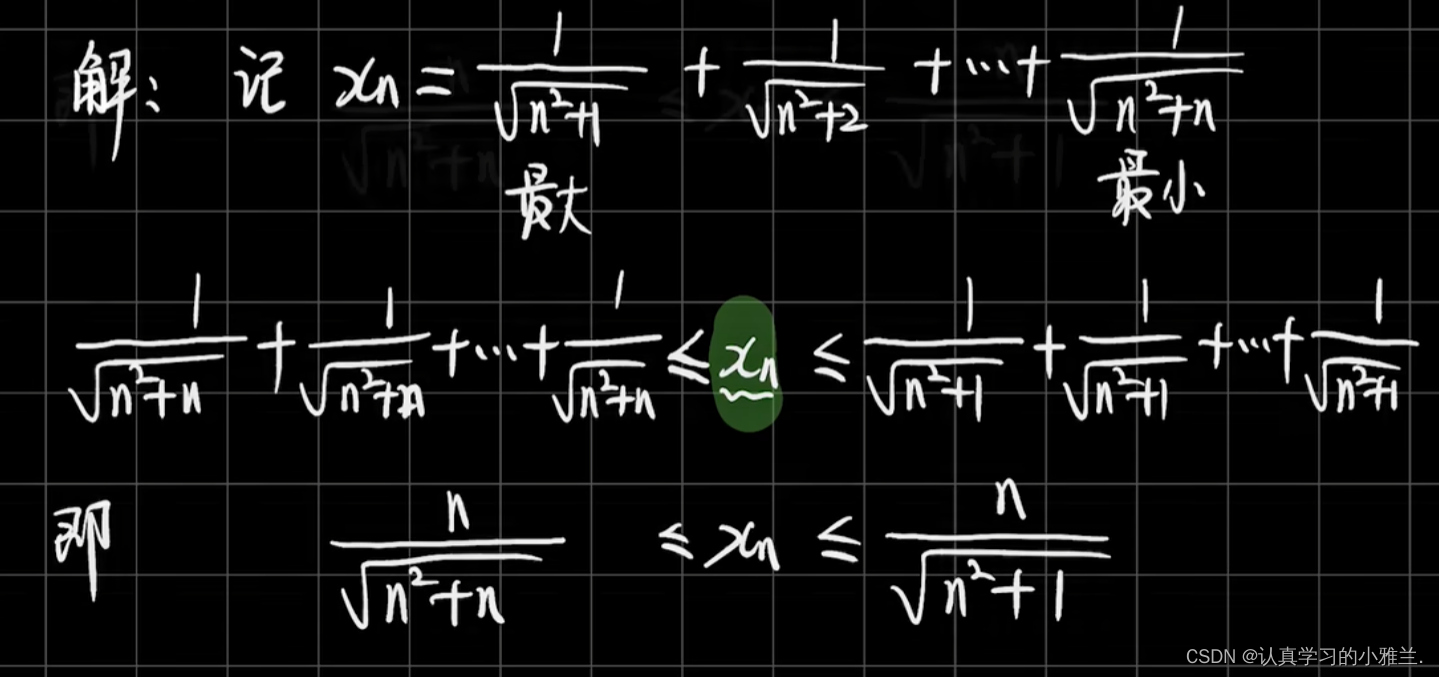
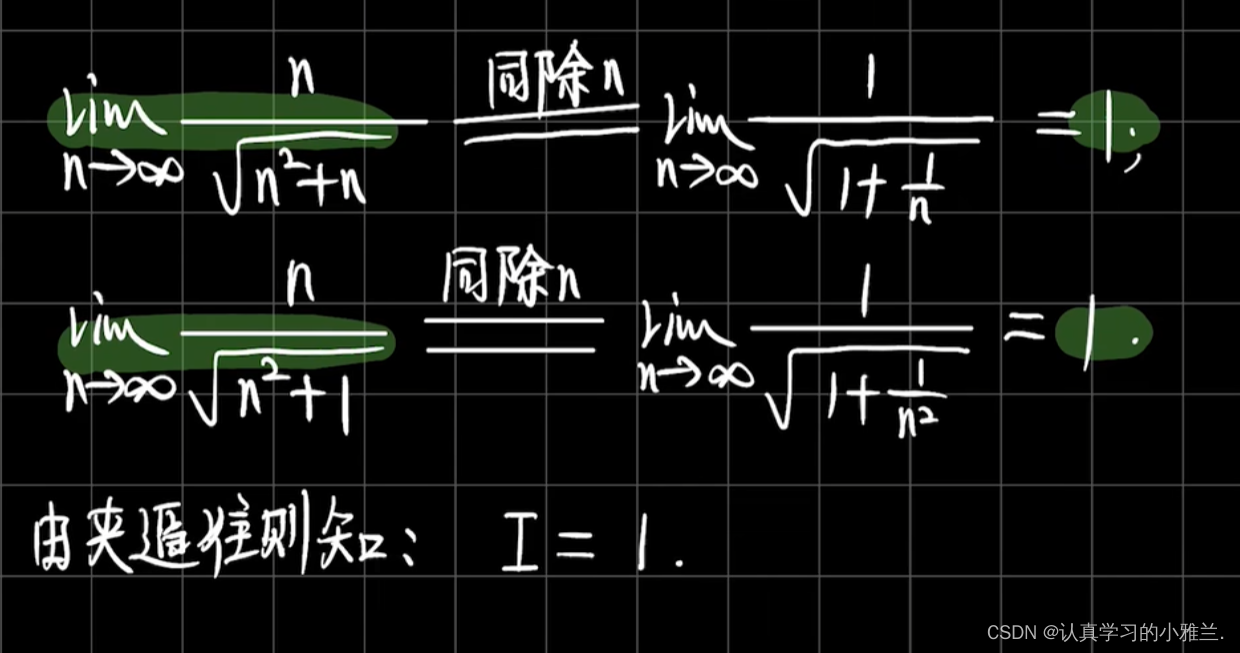
这样我们就完美解出了这道题目
下面，我们再来看一道例题
准则Ⅰ’ 函数的夹逼准则
一个是自变量趋于有限值时函数的极限 另一个是自变量趋于无穷时函数的极限
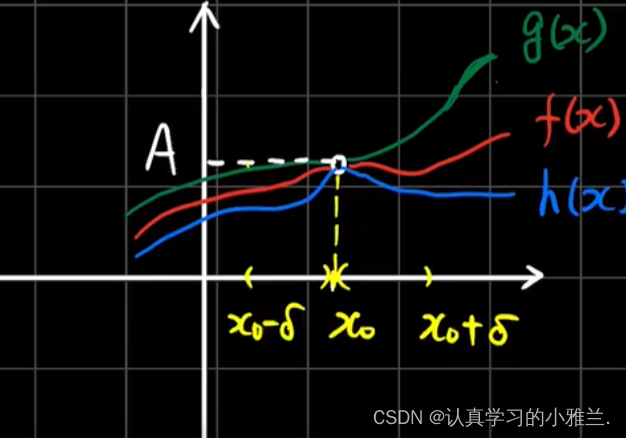
下面，我们来看一个例题来理解一下
二、重要极限Ⅰ
下面我们来证明一下此结论
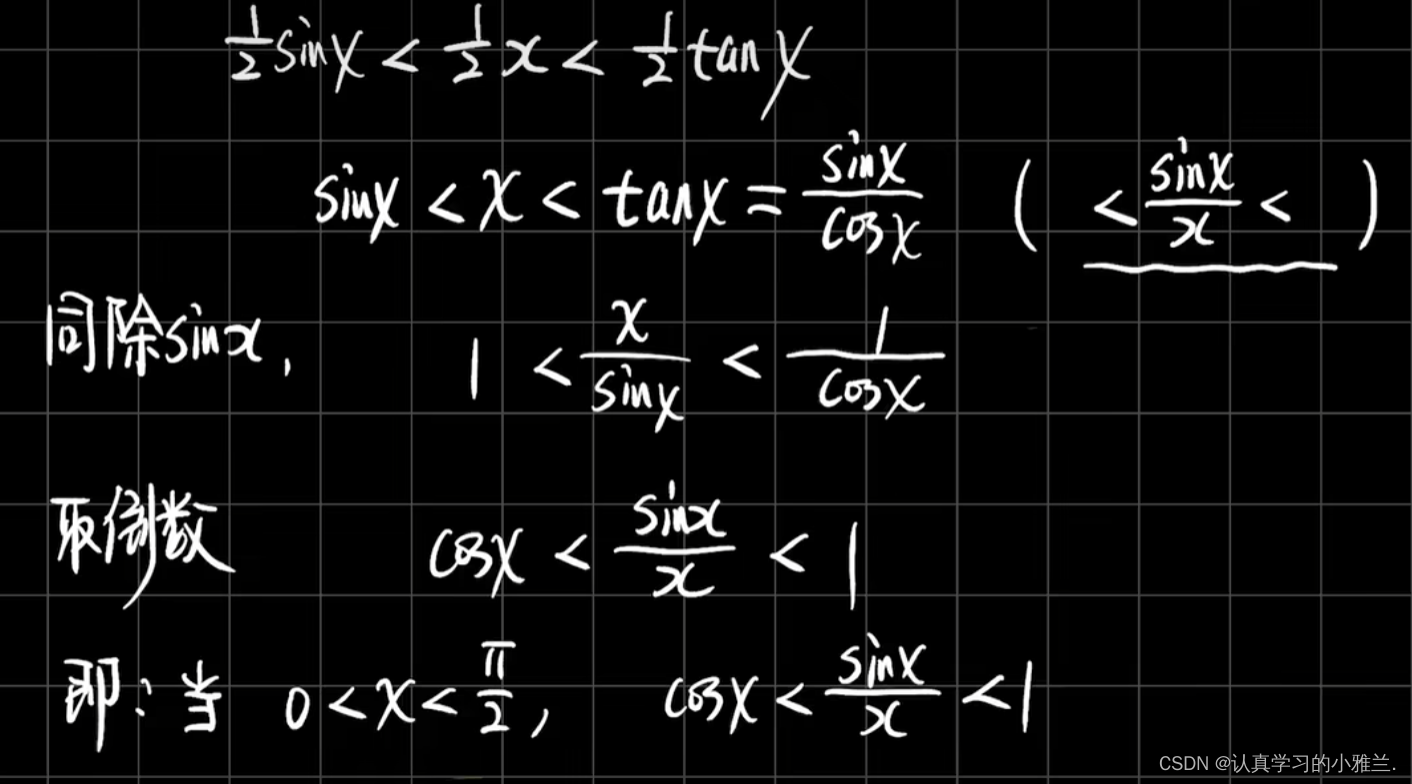
由二倍角公式 
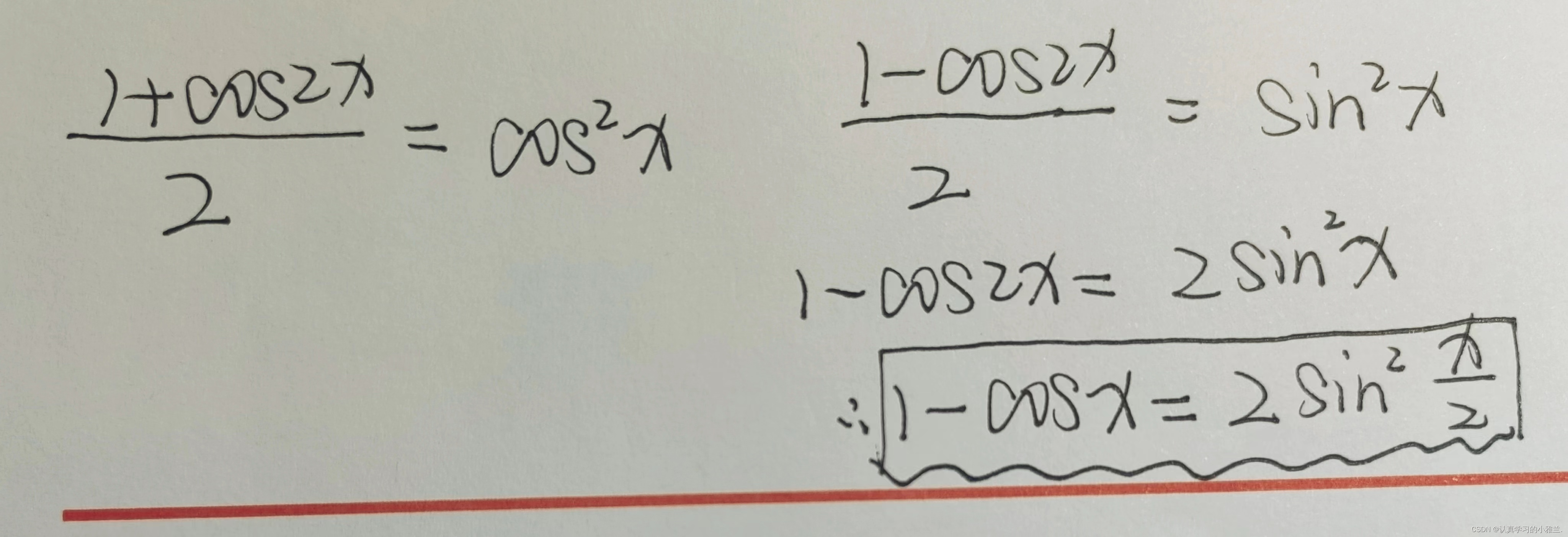
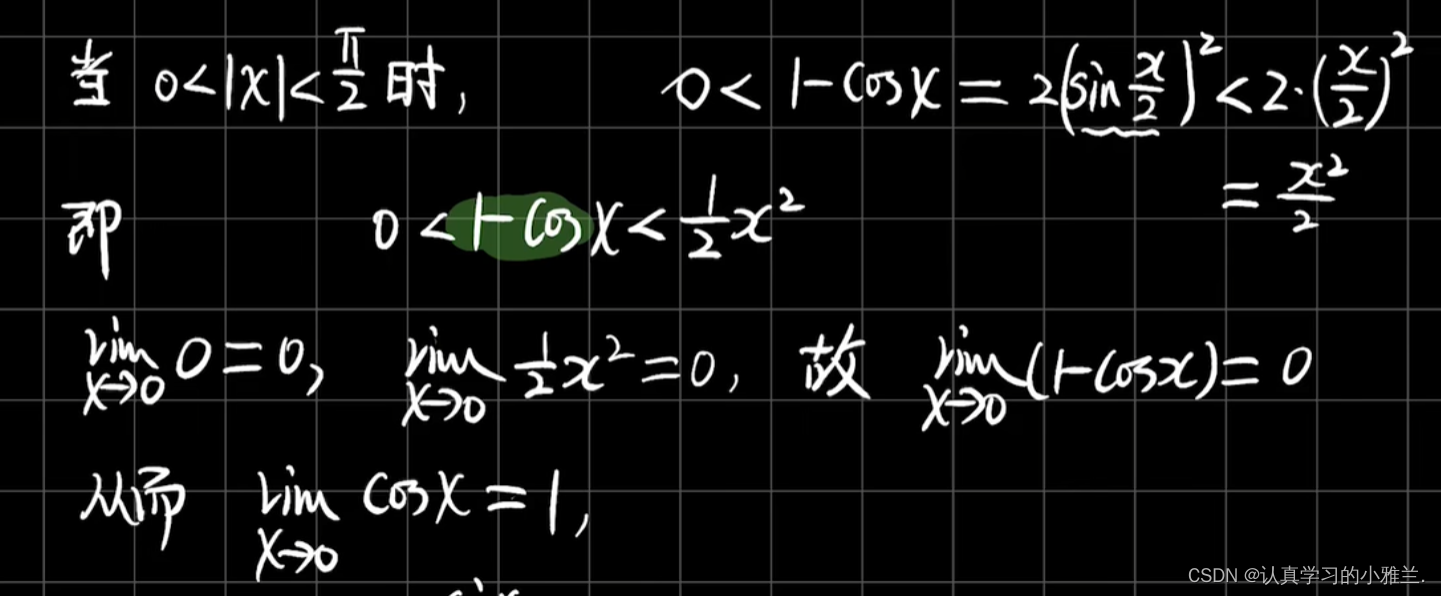
证明了此重要极限后，我们会意识到：光靠这样的形式，比较简单，是很难解出更多复杂的问题的，所以我们还有推广形式
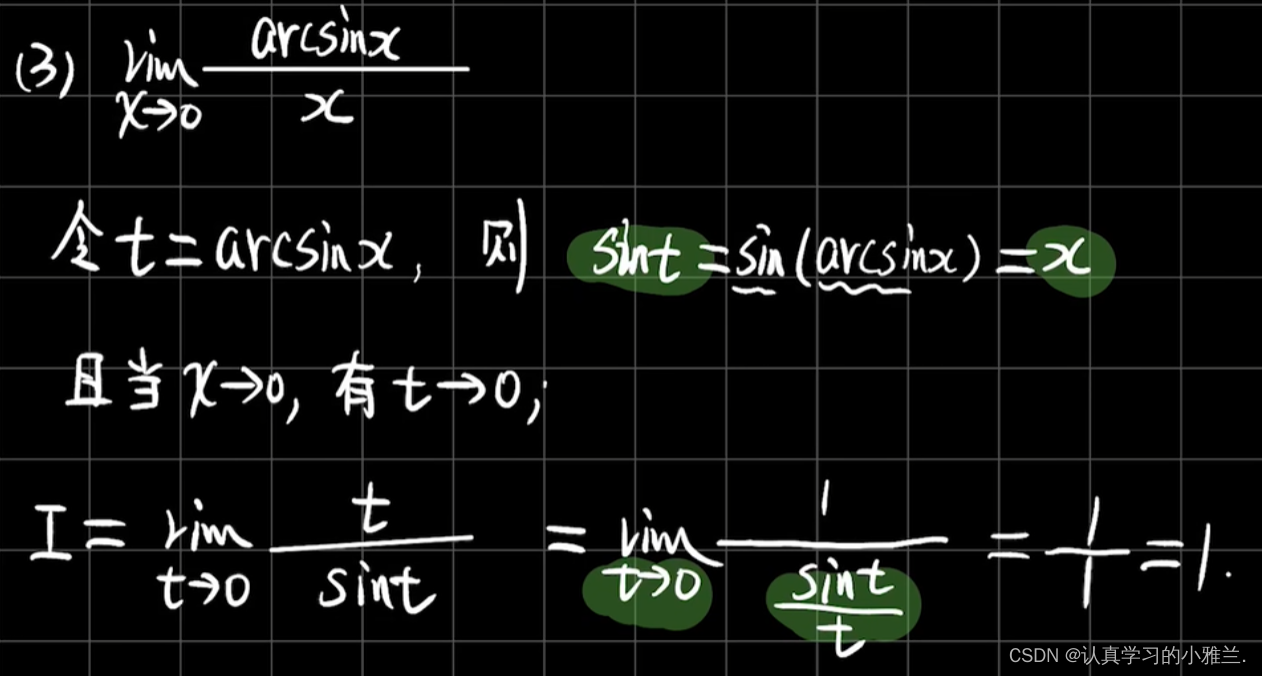
好，我们再来看几个小题，来更好地理解重要极限的推广形式
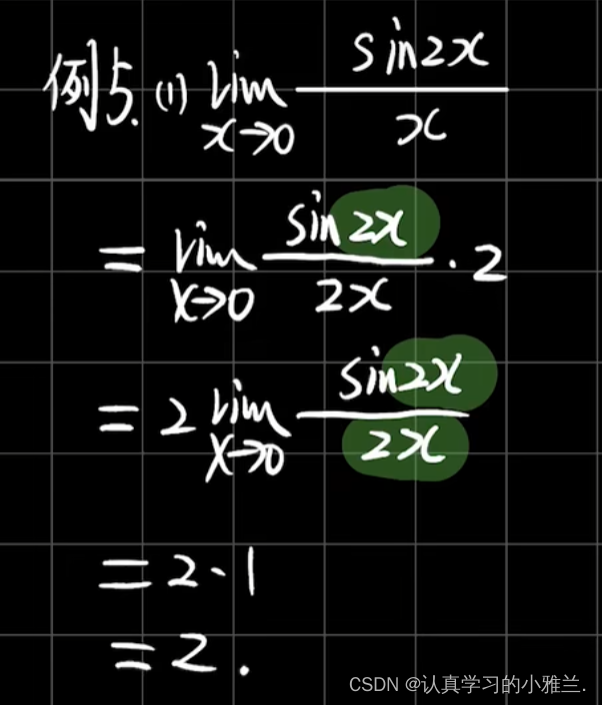
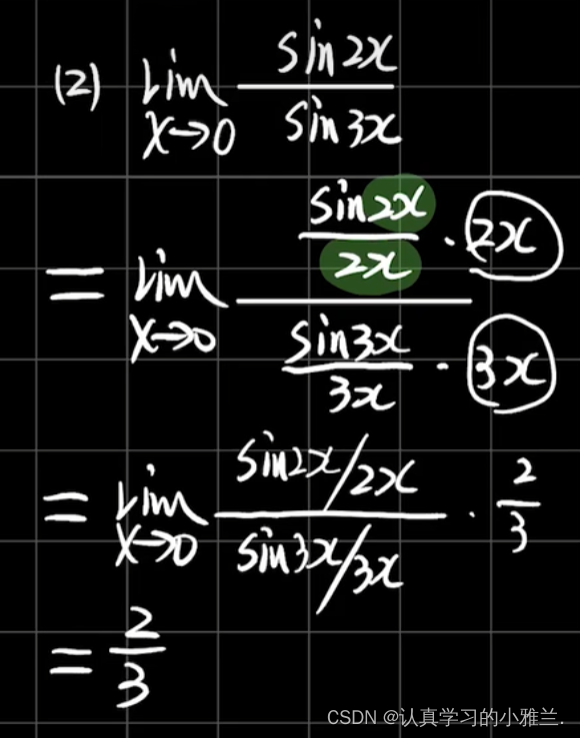
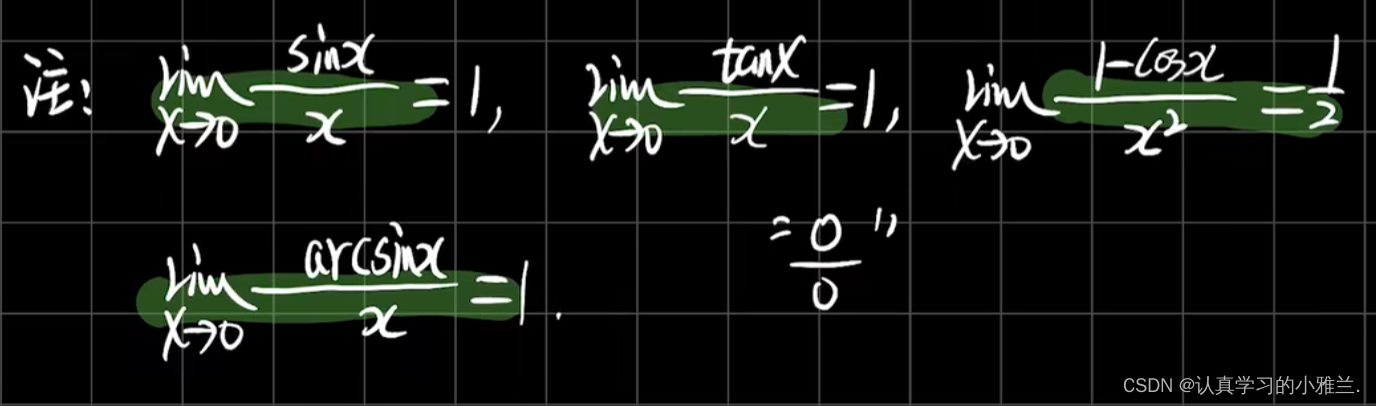易错题
这是我们上节课介绍过的：有界函数与无穷小的乘积是无穷小
三、准则Ⅱ 单调有界数列必有极限
这个数列不是单调数列
下面，我们再来看看单调数列的几何解释，因为用严格的定义证明已经超出了我们的能力范围
单调有界定理是数列收敛的充分条件
下面，我们来看一个例题
证明了这个数列的极限存在后，题目还要求我们求出这个极限
这个例题就是运用了一个套路来解题
这个建立极限值代数方程就是对求出的递推数列两边取极限
四、重要极限Ⅱ
意思是底数的极限无限趋于1，而不是底数就是1
现在开始证明此重要极限
我们首先要知道一个知识点，其实高中也学过，就是二项式定理
然后再证明单调性
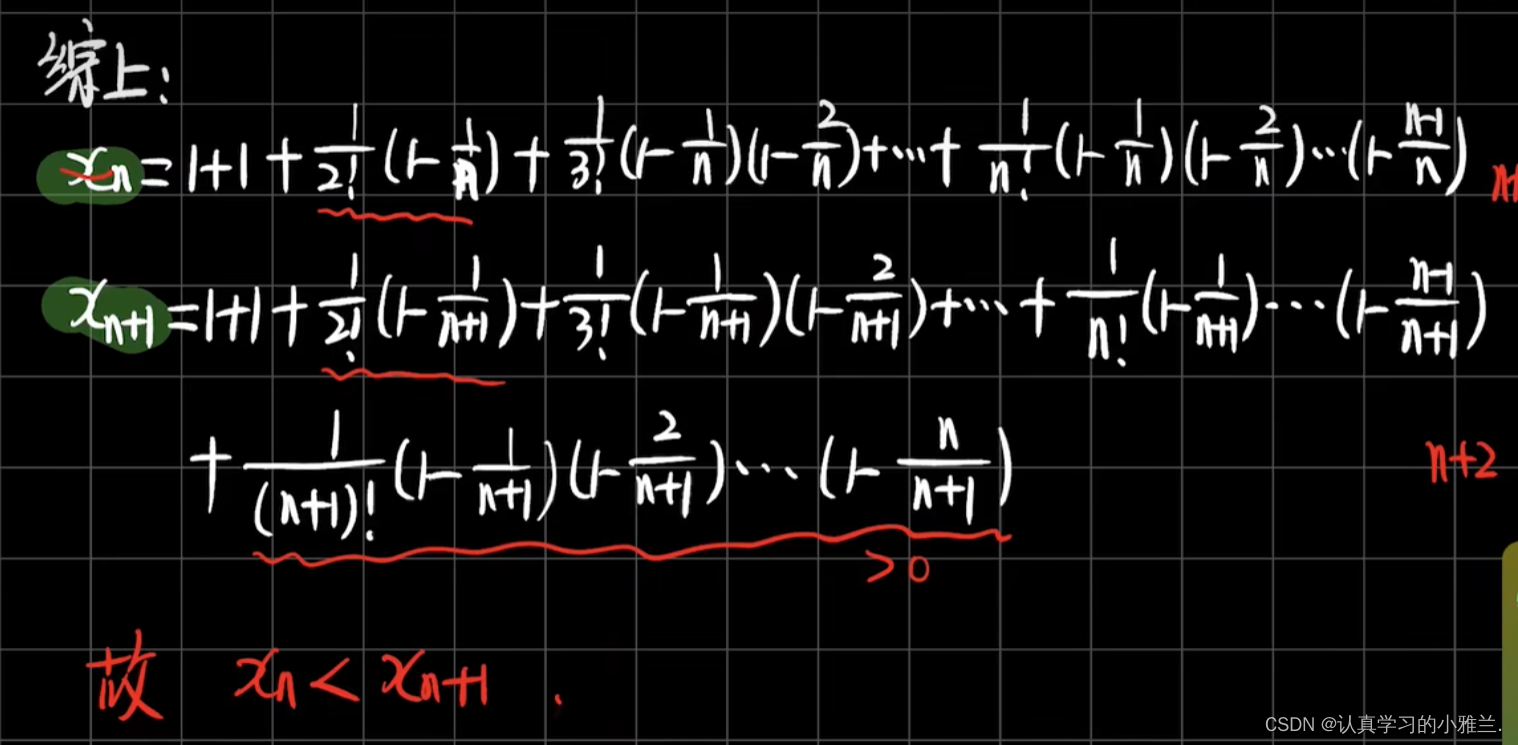所以数列xn是一个单调增加数列
证明有界性
下面，我们来看几个例题
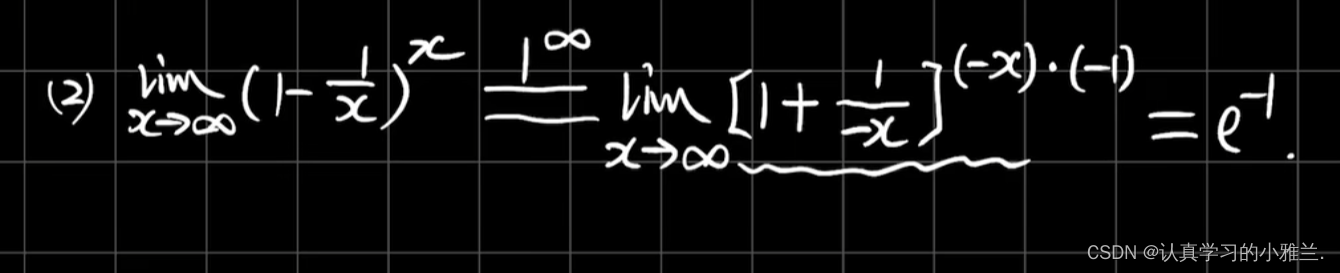
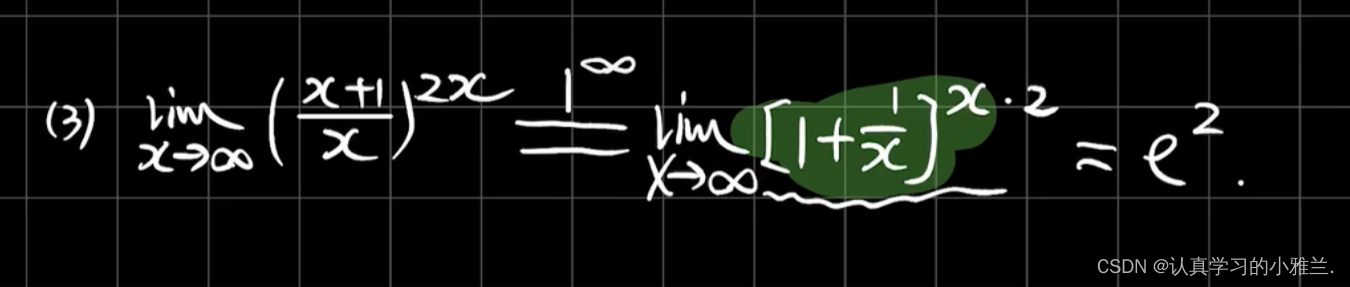
小结
好啦，那小雅兰今天学习的内容就到这里啦，还有很多内容需要学习，小雅兰会继续加油噢
