AcWing 1057. 股票买卖 IV
(1)问题

(2)分析
这道题我们首先得明确一点,我们只有一支股票,只是这支股票在不同天有着不同的价格,因此我们可以把天作为单位划分不同的状态。同时这道题中还有一个关键的信息,同一时刻,我们只能做一次交易,什么意思呢?即当这只股票在我们的手里的时候,我们无法再次进行购买,只能把这个股票卖出或者不卖。如果这支股票不在我们手里,那么我们只能选择买或者不买。
同时,题目还规定,买入股票和卖出股票算一次交易。因此,我们可以认为二者各算半次交易。由于只有手中有股票的时候才能卖出,说明再次之前已经买入。因此,我们可以在卖出股票的时候,把我们的交易次数+1。
a.状态定义
f
[
i
]
[
j
]
[
0
]
f[i][j][0]
f[i][j][0]表示在1到i天中买卖股票,当前已经进行了j次交易,且在第i天里,手中没有当前股票的时候,所得到的最大利润。
f
[
i
]
[
j
]
[
1
]
f[i][j][1]
f[i][j][1]表示在1到i天中买卖股票,当前已经进行了j次交易,且在第i天里,手中有当前股票的时候,所得到的最大利润。
b.状态转移
状态转移的话,我们可以画出下面的图,这样更加清晰:
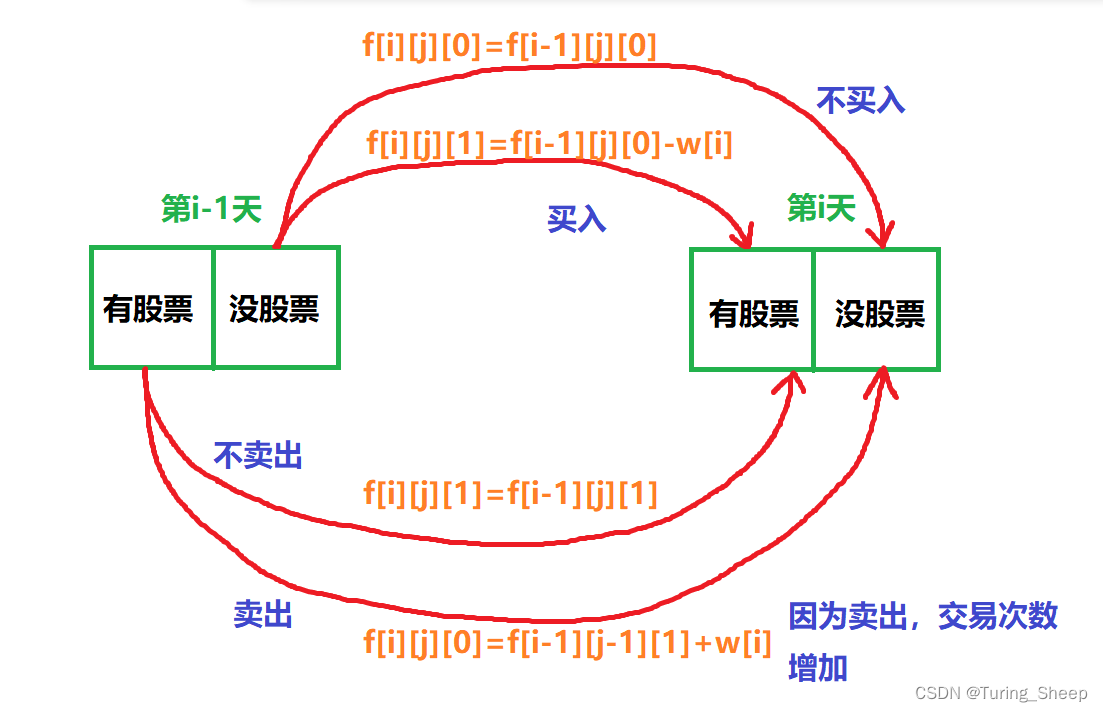
c.循环设计
这道股票的题其实如果不看状态之间的影响的话,其实就是一个01背包,因此我们按照01背包的逻辑来循环即可,即外层循环i,内层循环j。
d.初末状态
这里初始化比较麻烦,因为我们将卖出股票算作一次完整的交易,这一规定使得我们的初始化变得比较复杂。根据我们的规定,f[i][0][1]这种定义也是存在的,即从0到i中选一个最便宜的购入,就是当下的最优解。但是f[0][0][1]是不合法的,因此第0天的股票多贵不知道,没法买,而f[0][0][0]初始化为0即可,这个状态是存在的,第0天的股票虽然不存在,但是我们不买,依旧是0。
如果不想这么复杂的话,我们可以规定买入股票的时候,算一次完整的交易。此时我们发现f[i][0][1]是不合法的了。因为既然有股票,交易次数就不是0了。
(3)代码
规定卖出算一次交易
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=1e5+10,k=110;
int f[N][k][2],w[N];
int n,m;
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)scanf("%d",w+i);
memset(f,0xcf,sizeof f);
f[0][0][0]=0;
for(int i=1,minv = 1e6;i<=n;i++)
{
f[i][0][0]=0;
minv=min(minv,w[i]);
f[i][0][1]=-minv;
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
f[i][j][0]=max(f[i-1][j][0],f[i-1][j-1][1]+w[i]);
f[i][j][1]=max(f[i-1][j][1],f[i-1][j][0]-w[i]);
}
}
int res=0;
for(int i=0;i<=m;i++)res=max(f[n][i][0],res);
cout<<res<<endl;
return 0;
}
规定买入算一次交易
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=1e5+10,k=110;
int f[N][k][2],w[N];
int n,m;
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)scanf("%d",w+i);
memset(f,0xcf,sizeof f);
for(int i=0;i<=n;i++)f[i][0][0]=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
f[i][j][0]=max(f[i-1][j][0],f[i-1][j][1]+w[i]);
f[i][j][1]=max(f[i-1][j][1],f[i-1][j-1][0]-w[i]);
}
}
int res=0;
for(int i=0;i<=m;i++)res=max(f[n][i][0],res);
cout<<res<<endl;
return 0;
}