IIR滤波器的结构比较（Direct I and Direct II Form）

news2024/9/21 2:45:06

在 IIR 滤波器的设计和实现中，直接 I 型和直接 II 型结构的主要区别在于计算顺序和存储延迟项的方式。

直接I型结构

特点：

级联形式：直接I型结构的传递函数可以表示为两个级联部分：一个由分子系数组成的部分和一个由分母系数组成的部分。
计算顺序：输入信号首先通过分子多项式(零点多项式)，然后通过分母多项式（极点多项式）。（本质上是同时计算）
存储需求：需要存储所有的延迟变量。

结构：

$\frac{b_0 + b_1 z^{-1} + \cdots + b_M z^{-M}}{1 + a_1 z^{-1} + \cdots + a_N z^{-N}}$
输出 (y[n]) 可以通过以下公式计算：
$b_0 x[n] + b_1 x[n-1] + \cdots + b_M x[n-M] - a_1 y[n-1] - \cdots - a_N y[n-N]$
该结构中，直接实现了分子和分母多项式的差分方程。

优点：

实现简单：实现结构直接，容易理解和设计。
设计过程直观：适合初学者和简单滤波器设计。

缺点：

数值稳定性差：直接I型结构在一些情况下可能会有数值稳定性问题，特别是当滤波器阶数较高时。
1. 极点与零点的分布
  在直接I型结构中，输入信号首先通过分子多项式，然后通过分母多项式。这种结构方式使得
  滤波器的极点和零点在一个计算过程中紧密地耦合在一起。如果滤波器的极点靠近单位圆，滤
  波器的输出可能会变得不稳定，因为任何数值误差都会被极点放大，导致系统不稳定。
2. 数值误差的放大
  直接I型结构中的反馈路径容易引入并放大数值误差。特别是在高阶滤波器中，滤波器的系数
  可能有较大的范围差异，这会使得数值误差在计算过程中不断积累和放大，导致数值不稳定。
  这个问题在有限精度（例如浮点运算）的计算机系统中尤为明显。
3. 系数量化误差
  直接I型结构中，滤波器的分子和分母多项式的系数直接参与计算，任何系数的量化误差都会对
  滤波器的频率响应和稳定性产生影响。高阶滤波器的系数范围较广，量化误差可能会导致显著
  的数值不稳定。
4. 递归计算的累积误差
  直接I型结构的反馈部分（分母多项式部分）在计算时是递归的，这意味着当前输出不仅依赖于
  当前输入，还依赖于前几次的输出。因此，任何微小的误差都会在后续的计算中累积，导致数
  值不稳定。这种累积效应在高阶滤波器中尤为明显。
5. 直接II型结构的优势
  相比之下，直接II型结构通过状态变量表示，将滤波器的分子和分母多项式的计算分开处理，
  减少了直接耦合的复杂度。直接II型结构通过共享的延迟单元减少了存储需求，并且在计算
  时，分子和分母的系数误差不会互相放大。这使得直接II型结构在数值稳定性方面通常优于直
  接I型结构。
6. 总结
  直接I型结构数值稳定性差的原因主要在于极点与零点耦合导致的数值误差放大、递归计算的累
  积误差以及高阶滤波器系数范围较大导致的量化误差。而直接II型结构通过将分子和分母多项
  式计算分离、减少反馈路径上的误差放大，通常具有更好的数值稳定性。
存储开销大：由于需要存储全部的延迟单元，因为它需要存储输入和输出的延迟项，因此存储开销较大。
1. 对于一个三阶 IIR 滤波器（N=3），需要存储 3 个输入延迟项：x[n-1], x[n-2], x[n-3] 和 3个输出延迟项
  y[n-1], y[n-2], y[n-3]，总共 6 个状态变量

直接II型结构

特点：

级联形式：直接II型结构的传递函数也是由两个级联部分组成，但它们是分离的部分。
计算顺序：输入信号通过分母（极点）多项式，然后通过分子（零点）多项式。
存储需求：存储需求减少，因为它只需要存储中间变量的延迟项。

对于一个三阶 IIR 滤波器（N=3），需要存储 3 个延迟项 w[n-1], w[n-2], w[n-3]，总共 3 个
状态变量。

结构：

直接 II 型结构将传递函数分解为两个部分：分子部分和分母部分，并使用一个共享的延迟链。这种方式通过将滤波器的实现分成两步来减少存储需求。

计算中间变量 (w[n])：
$w[n] = x[n] - a_1 w[n-1] - a_2 w[n-2] - a_3 w[n-3]$
计算最终输出 (y[n])：
$y[n] = b_0 w[n] + b_1 w[n-1] + b_2 w[n-2] + b_3 w[n-3]$

这种结构中，输入信号和输出信号分别通过两个部分进行处理。

优点：

存储需求低：因为可以通过共享的延迟单元来实现，减少了存储需求。
数值稳定性好：通常比直接I型结构更稳定，先计算极点多项式，再零点多项式。

缺点：

实现复杂：实现过程稍微复杂一些，需要理解状态变量的概念。
设计较为复杂：适合高级应用和高阶滤波器设计。

import numpy as np
import matplotlib.pyplot as plt

# 定义滤波器系数
b = [0.0675, 0.2025, 0.2025, 0.0675]
a = [1.0, -1.1430, 0.4128, -0.0951]

# 输入信号：单位脉冲信号
n = 100  # 信号长度
x = np.zeros(n)
x[0] = 1  # 单位脉冲

# 直接I型结构
y_direct1 = np.zeros(n)
for i in range(3, n):
    y_direct1[i] = (b[0]*x[i] + b[1]*x[i-1] + b[2]*x[i-2] + b[3]*x[i-3] -
                    a[1]*y_direct1[i-1] - a[2]*y_direct1[i-2] - a[3]*y_direct1[i-3])

# 直接II型结构
w = np.zeros(n)
y_direct2 = np.zeros(n)
for i in range(3, n):
    w[i] = x[i] - a[1]*w[i-1] - a[2]*w[i-2] - a[3]*w[i-3]
    y_direct2[i] = b[0]*w[i] + b[1]*w[i-1] + b[2]*w[i-2] + b[3]*w[i-3]

# 绘制结果
plt.figure(figsize=(12, 6))
plt.plot(y_direct1, label='Direct I Structure')
plt.plot(y_direct2, label='Direct II Structure')
plt.legend()
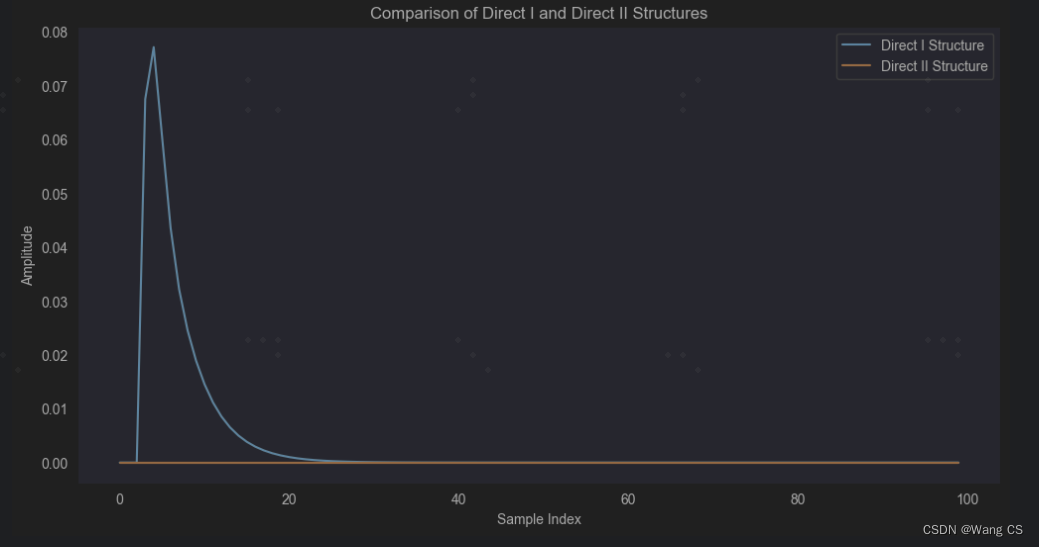
plt.title('Comparison of Direct I and Direct II Structures')
plt.xlabel('Sample Index')
plt.ylabel('Amplitude')
plt.grid()
plt.show()