队列和栈的实现

news2024/11/27 5:27:42

文章目录

  • 队列
    • 队列的定义
    • 队列常见的基本操作
    • 队列的顺序存储结构
    • 实现
  • 栈
    • 栈的定义
    • 栈的常见基本操作
    • 栈的顺序存储
      • 实现
    • 栈的链式存储
      • 实现

队列

队列的定义

 队列（queue）是只允许在一端进行插入操作，而在另一端进行删除操作的线性表。队列是一种先进先出（First In First Out）的线性表，简称FIFO。允许插入的一端称为队尾，允许删除的一端称为队头。
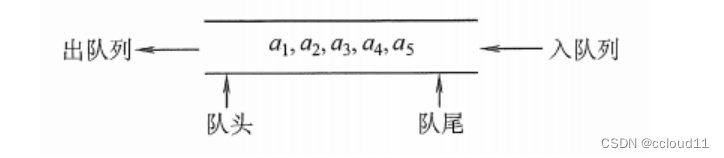
在这里插入图片描述
队头（Front）：允许删除的一端，又称队首。
队尾（Rear）：允许插入的一端。
空队列：不包含任何元素的空表。

队列常见的基本操作

nitQueue(&Q)：初始化队列，构造一个空队列Q。
QueueEmpty(Q)：判队列空，若队列Q为空返回true，否则返回false。
EnQueue(&Q, x)：入队，若队列Q未满，将x加入，使之成为新的队尾。
DeQueue(&Q, &x)：出队，若队列Q非空，删除队头元素，并用x返回。
GetHead(Q, &x)：读队头元素，若队列Q非空，则将队头元素赋值给x。

队列的顺序存储结构

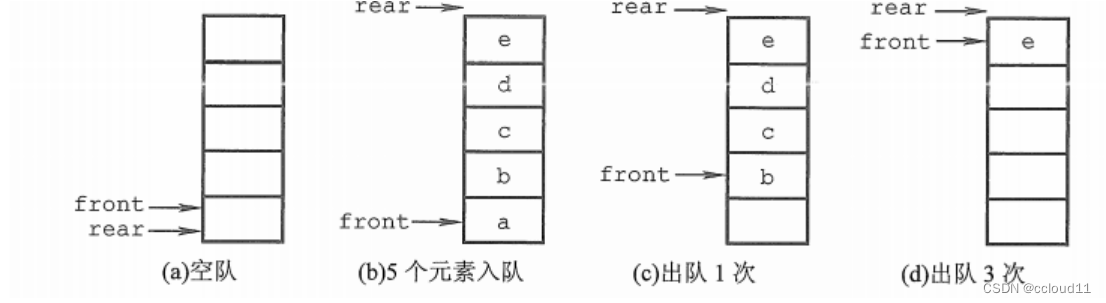
初始状态（队空条件）：Q->front == Q->rear == 0。
进队操作：队不满时，先送值到队尾元素，再将队尾指针加1。
出队操作：队不空时，先取队头元素值，再将队头指针加1。
在这里插入图片描述

实现

SeqQueue.h

#pragma once
#ifndef SEQQUEUE_H
#define SEQQUEUE_H

#define MAX_SIZE 1024

#include <stdio.h>
#include <stdlib.h>

typedef struct SEQQUEUE_H {
	void* data[MAX_SIZE];
	int size;
}SeqQueue;

//初始化 //入列//返回队头元素//出队//返回队尾元素//返回大小//清空队列//销毁
SeqQueue* Init_SeqQueue();
//入列
void Push_SeqQueue(SeqQueue* queue, void* data);
//返回队头元素
void* Front_SeqQueue(SeqQueue* queue);
//出队
void Pop_SeqQueue(SeqQueue* queue);
//返回队尾元素
void* Back_SeqQueue(SeqQueue* queue);
//返回大小
int Size_SeqQueue(SeqQueue* queue);
//清空队列
void Clear_SeqQueue(SeqQueue* queue);
//销毁
void FreeSpace_SeqQueue(SeqQueue* queue);

#endif // !SEQQUEUE_H

SeqQueue.c

#include "SeqQueue.h"

//初始化 //入列//返回队头元素//出队//返回队尾元素//返回大小//清空队列//销毁
SeqQueue* Init_SeqQueue()
{
	SeqQueue* queue = (SeqQueue*)malloc(sizeof(SeqQueue));
	for (int i = 0; i < MAX_SIZE; i++)
	{
		queue->data[i] = NULL;
	}
	queue->size = 0;

	return queue;
}

//入列
void Push_SeqQueue(SeqQueue* queue, void* data)
{
	if (!queue || !data)
	{
		return;
	}

	if (queue->size == MAX_SIZE)
	{
		return;
	}

	queue->data[queue->size] = data;
	queue->size++;
}

//返回队头元素
void* Front_SeqQueue(SeqQueue* queue)
{
	if (!queue)
	{
		return NULL;
	}

	if (queue->size == 0)
	{
		return NULL;
	}

	return queue->data[0];
}

//出队
void Pop_SeqQueue(SeqQueue* queue)
{
	if (!queue)
	{
		return;
	}

	if (queue->size == 0)
	{
		return;
	}

	for (int i = 0; i < queue->size - 1; i++)
	{
		queue->data[i] = queue->data[i + 1];
	}

	queue->size--;
}

//返回队尾元素
void* Back_SeqQueue(SeqQueue* queue)
{
	if (!queue)
	{
		return NULL;
	}

	if (queue->size == 0)
	{
		return NULL;
	}

	return queue->data[queue->size - 1];
}

//返回大小
int Size_SeqQueue(SeqQueue* queue)
{
	if (!queue)
	{
		return -1;
	}

	return queue->size;
}

//清空队列
void Clear_SeqQueue(SeqQueue* queue)
{
	if (!queue)
	{
		return;
	}

	queue->size = 0;
}

//销毁
void FreeSpace_SeqQueue(SeqQueue* queue)
{
	if (!queue)
	{
		return;
	}

	free(queue);
}

main.c

#include "SeqQueue.h"

typedef struct PERXON {
	char name[64];
	int age;
}Person;

int main()
{
	//创建队列
	SeqQueue* queue = Init_SeqQueue();
	//创建数据
	Person p1 = { "aaa", 10 };
	Person p2 = { "bbb", 20 };
	Person p3 = { "ccc", 30 };
	Person p4 = { "ddd", 40 };
	Person p5 = { "eee", 50 };

	//数据入队列
	Push_SeqQueue(queue, &p1);
	Push_SeqQueue(queue, &p2);
	Push_SeqQueue(queue, &p3);
	Push_SeqQueue(queue, &p4);
	Push_SeqQueue(queue, &p5);

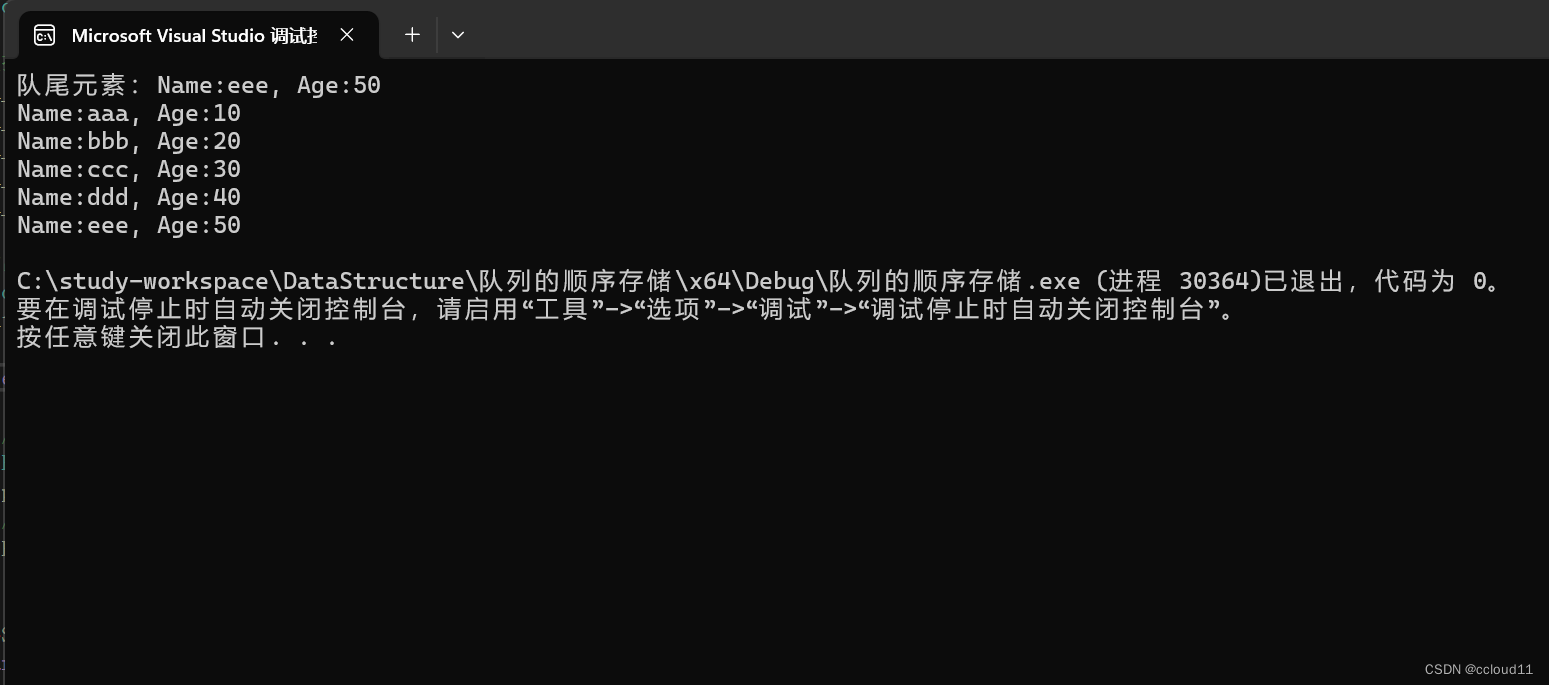
	//输出队尾元素
	Person* backPerson = (Person*)Back_SeqQueue(queue);
	printf("队尾元素：Name:%s, Age:%d\n", backPerson->name, backPerson->age);

	while (Size_SeqQueue(queue))
	{
		//取出队头元素
		Person* p = (Person*)Front_SeqQueue(queue);
		printf("Name:%s, Age:%d\n", p->name, p->age);
		//从队头弹出
		Pop_SeqQueue(queue);
	}

	FreeSpace_SeqQueue(queue);
	return 0; 
}

在这里插入图片描述

栈

栈的定义

 栈（Stack）：是只允许在一端进行插入或删除的线性表。首先栈是一种线性表，但限定这种线性表只能在某一端进行插入和删除操作。
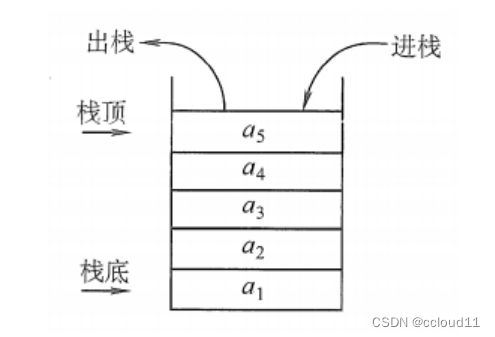
在这里插入图片描述
栈顶（Top）：线性表允许进行插入删除的那一端。
栈底（Bottom）：固定的，不允许进行插入和删除的另一端。
空栈：不含任何元素的空表。
栈又称为后进先出（Last In First Out）的线性表，简称LIFO结构。

栈的常见基本操作

InitStack(&S)：初始化一个空栈S。
StackEmpty(S)：判断一个栈是否为空，若栈为空则返回true，否则返回false。
Push(&S, x)：进栈（栈的插入操作），若栈S未满，则将x加入使之成为新栈顶。
Pop(&S, &x)：出栈（栈的删除操作），若栈S非空，则弹出栈顶元素，并用x返回。
GetTop(S, &x)：读栈顶元素，若栈S非空，则用x返回栈顶元素。
DestroyStack(&S)：栈销毁，并释放S占用的存储空间（“&”表示引用调用）。

栈的顺序存储

 采用顺序存储的栈称为顺序栈，它利用一组地址连续的存储单元存放自栈底到栈顶的数据元素，同时附设一个指针（top）指示当前栈顶元素的位置。
若存储栈的长度为StackSize，则栈顶位置top必须小于StackSize。当栈存在一个元素时，top等于0，因此通常把空栈的判断条件定位top等于-1。

实现

SeqStack.h

#pragma once
#ifndef SEQSTACK_H
#define SEQSTACK_H

#include <stdio.h>
#include <stdlib.h>

//数组去模拟栈的顺序存储
#define MAX_SIZE 1024
#define SEQSTACK_TRUE 1
#define SEQSTACK_FALSE 0

typedef struct SEQSTACK {
	void* data[MAX_SIZE];
	int size;
}SeqStack;

//初始化栈 
SeqStack* Init_SeqStack();
//入栈
void Push_SeqStack(SeqStack* stack, void* data);
//返回栈顶元素
void* Top_SeqStack(SeqStack* stack);
//出栈
void Pop_SeqStack(SeqStack* stack);
//判断是否为空
int IsEmpty(SeqStack* stack);
//返回栈中元素的个数
int Size_SeqStack(SeqStack* stack);
//清空栈
void Clear_SeqStack(SeqStack* stack);
//销毁
void FreeSpace_SeqStack(SeqStack* stack);
#endif // !SEQSTACK_H

SeqStack.c

#include "SeqStack.h"

//初始化栈 
SeqStack* Init_SeqStack()
{
	SeqStack* stack = (SeqStack*)malloc(sizeof(SeqStack));

	for (int i = 0; i < MAX_SIZE; i++)
	{
		stack->data[i] = NULL;
	}
	stack->size = 0;

	return stack;
}

//入栈
void Push_SeqStack(SeqStack* stack, void* data)
{
	if (!stack || !data)
	{
		return;
	}

	if (stack->size == MAX_SIZE)
	{
		return;
	}

	stack->data[stack->size] = data;
	stack->size++;
}
//返回栈顶元素
void* Top_SeqStack(SeqStack* stack)
{
	if (stack == NULL)
	{
		return NULL;
	}

	if (stack->size == 0)
	{
		return NULL;
	}

	return stack->data[stack->size - 1];
}
//出栈
void Pop_SeqStack(SeqStack* stack)
{
	if (stack == NULL)
	{
		return;
	}

	if (stack->size == 0)
	{
		return;
	}

	stack->data[stack->size - 1] = NULL;
	stack->size--;
}

//判断是否为空
int IsEmpty(SeqStack* stack)
{
	if (stack == NULL)
	{
		return -1;
	}

	if(stack->size == 0)
	{
		return SEQSTACK_TRUE;
	}

	return SEQSTACK_FALSE;
}

//返回栈中元素的个数
int Size_SeqStack(SeqStack* stack)
{
	return stack->size;
}

//清空栈
void Clear_SeqStack(SeqStack* stack)
{
	if(stack == NULL)
	{
		return;
	}

	for (int i = 0; i < stack->size; i++)
	{
		stack->data[i] = NULL;
	}

	stack->size = 0;
}

//销毁
void FreeSpace_SeqStack(SeqStack* stack)
{
	if (stack == NULL)
	{
		return;
	}

	free(stack);
}

main.c

#include "SeqStack.h"

typedef struct PERSON 
{
	char name[64];
	int age;
}Person;



int main()
{
	//创建栈
	SeqStack* stack = Init_SeqStack();

	//创建数据
	Person p1 = { "aaa", 10 };
	Person p2 = { "bbb", 20 };
	Person p3 = { "ccc", 30 };
	Person p4 = { "ddd", 40 };
	Person p5 = { "eee", 50 };

	//入栈
	Push_SeqStack(stack, &p1);
	Push_SeqStack(stack, &p2);
	Push_SeqStack(stack, &p3);
	Push_SeqStack(stack, &p4);
	Push_SeqStack(stack, &p5);

	//输出
	while (!IsEmpty(stack))
	{
		Person * person = (Person *) Top_SeqStack(stack);
		printf("%s->%d\n", person->name, person->age);

		Pop_SeqStack(stack);
	}

	FreeSpace_SeqStack(stack);
	return 0;
}

在这里插入图片描述

栈的链式存储

 采用链式存储的栈称为链栈，链栈的优点是便于多个栈共享存储空间和提高其效率，且不存在栈满上溢的情况。通常采用单链表实现，并规定所有操作都是在单链表的表头进行的。这里规定链栈没有头节点，Lhead指向栈顶元素，如下图所示。
在这里插入图片描述

实现

LinkStack.h

#pragma once
#ifndef LINKSTACK_H
#define LINKSTACK_H

#include <stdio.h>
#include <stdlib.h>

//链式栈的结点
typedef struct LINKNODE {
	struct LINKNODE* next;
}LinkNode;
//链式栈
typedef struct LINKSTACK {
	LinkNode head;
	int size;
}LinkStack;

//初始化函数
LinkStack* Init_LinkStack();
//入栈
void Push_LinkStack(LinkStack* stack, LinkNode* data);
//出栈
void Pop_LinkStack(LinkStack* stack);
//返回栈顶元素
LinkNode* Top_LinkStack(LinkStack* stack);
//返回栈元素的个数
int Size_LinkStack(LinkStack* stack);
//清空栈
void clear_LinkStack(LinkStack* stack);
//销毁栈
void FreeSpace_LinkStack(LinkStack* stack);

#endif // !LINKSTACK_H

LinkStack.c

#include "LinkStack.h"

//初始化函数
LinkStack* Init_LinkStack()
{
	LinkStack* stack = (LinkStack*)malloc(sizeof(LinkStack));
	stack->head.next = NULL;
	stack->size = 0;

	return stack;
}

//入栈
void Push_LinkStack(LinkStack* stack, LinkNode* data)
{
	if (!stack || !data)
	{
		return;
	}

	data->next = stack->head.next;
	stack->head.next = data;
	stack->size++;
}

//出栈
void Pop_LinkStack(LinkStack* stack)
{
	if (!stack)
	{
		return;
	}

	if (stack->size == 0)
	{
		return;
	}

	LinkNode* pCurrent = stack->head.next;
	stack->head.next = pCurrent->next;

	stack->size--;
}
//返回栈顶元素
LinkNode* Top_LinkStack(LinkStack* stack)
{
	if (!stack)
	{
		return NULL;
	}

	if (stack->size == 0)
	{
		return NULL;
	}

	return stack->head.next;
}

//返回栈元素的个数
int Size_LinkStack(LinkStack* stack)
{
	return stack->size;
}

//清空栈
void clear_LinkStack(LinkStack* stack)
{
	if (!stack)
	{
		return;
	}

	if (stack->size == 0)
	{
		return;
	}

	stack->head.next = NULL;
	stack->size = 0;
}

//销毁栈
void FreeSpace_LinkStack(LinkStack* stack)
{
	if (!stack)
	{
		return;
	}

	free(stack);
}

main.c

#include "LinkStack.h"

typedef struct PERSON
{
	LinkNode node;
	char name[64];
	int age;
}Person;

int main()
{
	//创建栈
	LinkStack* stack = Init_LinkStack();
	//创建数据
	Person p1, p2, p3, p4, p5;
	strcpy(p1.name, "aaa");
	strcpy(p2.name, "bbb");
	strcpy(p3.name, "ccc");
	strcpy(p4.name, "ddd");
	strcpy(p5.name, "eee");

	p1.age = 10;
	p2.age = 20;
	p3.age = 30;
	p4.age = 40;
	p5.age = 50;

	//入栈
	Push_LinkStack(stack, (LinkNode*)&p1);
	Push_LinkStack(stack, (LinkNode*)&p2);
	Push_LinkStack(stack, (LinkNode*)&p3);
	Push_LinkStack(stack, (LinkNode*)&p4);
	Push_LinkStack(stack, (LinkNode*)&p5);

	while (Size_LinkStack(stack))
	{
		//取出栈顶元素
		Person* p = (Person*)Top_LinkStack(stack);
		printf("Name:%s Age:%d\n", p->name, p->age);
		//弹出栈顶元素
		Pop_LinkStack(stack);
	}

	FreeSpace_LinkStack(stack);

	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1808590.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

翻译《The Old New Thing》- Why do messages posted by PostThreadMessage disappear?

翻译《The Old New Thing》- Why do messages posted by PostThreadMessage disappear?

Why do messages posted by PostThreadMessage disappear? - The Old New Thing (microsoft.com)https://devblogs.microsoft.com/oldnewthing/20090930-00/?p16553 Raymond Chen 2008年09月30日 为什么 PostThreadMessage 发布的信息会消失&#xff1f; 在显示用户界面的线…
阅读更多...
【上下界分析 差分数组】798得分最高的最小轮调

【上下界分析 差分数组】798得分最高的最小轮调

本文涉及知识点 差分数组 本题同解 C算法前缀和的应用&#xff1a;798得分最高的最小轮调 LeetCode798得分最高的最小轮调 给你一个数组 nums&#xff0c;我们可以将它按一个非负整数 k 进行轮调&#xff0c;这样可以使数组变为 [nums[k], nums[k 1], … nums[nums.lengt…
阅读更多...
NetSuite精益实施 之 系统切换作业标准化

NetSuite精益实施 之 系统切换作业标准化

这个题目为近日所思&#xff0c;一直没有落笔。今天是端午假日&#xff0c;得空卸货。 标准化是精益实施的三个基础之一&#xff0c;在我们的项目实践中没有须臾忘记。在此我们不再赘述标准化为啥这么重要&#xff0c;更多来分享如何标准化。 在项目实施的各阶段中&#xff0…
阅读更多...
【漏洞复现】宏景eHR pos_dept_post SQL注入漏洞

【漏洞复现】宏景eHR pos_dept_post SQL注入漏洞

0x01 产品简介 宏景eHR人力资源管理软件是一款人力资源管理与数字化应用相融合&#xff0c;满足动态化、协同化、流程化、战略化需求的软件。 0x02 漏洞概述 宏景eHR pos_dept_post 接囗处存在SQL注入漏洞,未经过身份认证的远程攻击者利用此漏洞执行任意SQL指令&#xff0c;…
阅读更多...
每日一题——Python实现PAT乙级1019 数字黑洞（举一反三+思想解读+逐步优化）

每日一题——Python实现PAT乙级1019 数字黑洞（举一反三+思想解读+逐步优化）

一个认为一切根源都是“自己不够强”的INTJ 个人主页&#xff1a;用哲学编程-CSDN博客专栏&#xff1a;每日一题——举一反三Python编程学习Python内置函数 Python-3.12.0文档解读 目录 我的写法 点评代码的优缺点&#xff1a; 时间复杂度&#xff1a; 空间复杂度&#…
阅读更多...
数据结构：插入排序和希尔排序

数据结构：插入排序和希尔排序

插入排序 逆序的情况下&#xff1a; 时间复杂度&#xff1a;O(N^2) 空间复杂度&#xff1a;O(1) 顺序的情况下&#xff1a; 时间复杂度&#xff1a;O(N) 空间复杂度…
阅读更多...
【Linux系统化学习】传输层——TCP协议

【Linux系统化学习】传输层——TCP协议

目录 预备知识 全双工协议 协议缓冲区 TCP协议 TCP协议格式 六个标志位 两个问题 确认应答机制 流量控制 超时重传机制 连接管理机制 CLOSE_WAIT状态 TIME_WAIT状态 滑动窗口 拥塞控制 延迟应答 捎带应答 粘包问题 TCP的异常情况 TCP小结 TCP/UDP协议对比…
阅读更多...
首届IEEE RAS峰会，为什么大厂阿里、字节、腾讯都参加了？

首届IEEE RAS峰会，为什么大厂阿里、字节、腾讯都参加了？

"RAS in Data Centers 2024" 首届IEEE RAS&#xff08;Reliability, Availability, and Serviceability&#xff0c;即可靠性、可用性和可维护性&#xff09;在数据中心峰会在2024年6月11日至12日举行&#xff0c;地点设在美国加利福尼亚州圣克拉拉市的圣克拉拉万豪酒…
阅读更多...
LangChain开发【NL2SQL】应用（few-shot优化）

LangChain开发【NL2SQL】应用（few-shot优化）

前言 之前发布的博客LangGraph开发Agent智能体应用【NL2SQL】-CSDN博客&#xff0c;留了一个问题&#xff0c;对于相对复杂的sql&#xff08;leetcode中等难度的sql题&#xff09;&#xff0c;gpt4o就力不从心了。这篇文章来讲一下优化 什么是few-shot 使用这些少量的、调整…
阅读更多...
公安视频图像信息数据库及GA/T 1400视图库视频监控系统的使用场景

公安视频图像信息数据库及GA/T 1400视图库视频监控系统的使用场景

随着科技的快速发展&#xff0c;大数据、人工智能等新技术不断融入各行各业&#xff0c;为各行各业带来了前所未有的变革。在公安领域&#xff0c;GA/T 1400协议公安视频图像信息数据库的应用为视频监控场景提供了强有力的支持&#xff0c;极大地提升了公安工作的效率和准确性。…
阅读更多...
排序-快排算法对数组进行排序

排序-快排算法对数组进行排序

目录 一、问题描述 二、解题思路 1.初始化 2.将右侧小于基准元素移到左边 3.将左侧大于基准元素移到右边 4.重复执行上面的操作 5.对分好的左、右分区再次执行分区操作 6.最终排序结果 三、代码实现 四、刷题链接 一、问题描述 二、解题思路 快排算法实现数组排序&am…
阅读更多...
算法金 | A - Z，115 个数据科学 机器学习 江湖黑话（全面）

算法金 | A - Z，115 个数据科学 机器学习 江湖黑话（全面）

大侠幸会&#xff0c;在下全网同名「算法金」 0 基础转 AI 上岸&#xff0c;多个算法赛 Top 「日更万日&#xff0c;让更多人享受智能乐趣」 机器学习本质上和数据科学一样都是依赖概率统计&#xff0c;今天整整那些听起来让人头大的机器学习江湖黑话 A - C A/B Testing (A/B …
阅读更多...
保姆级讲解 Linux下FTP服务器的搭建、配置与管理

保姆级讲解 Linux下FTP服务器的搭建、配置与管理

本来目录很长的 因为感觉不太美观 所以小标题都删掉了 本文介绍了 本地用户的FTP服务器搭建实例匿名用户的FTP服务器搭建实例虚拟用户的FTP服务器搭建实例企业常见类型搭建实验 配置与管理FTP服务器 配置与管理FTP服务器一、FTP相关知识二、项目设计与准备三、项目实施四、认识…
阅读更多...
存内计算与扩散模型：下一代视觉AIGC能力提升的关键

存内计算与扩散模型：下一代视觉AIGC能力提升的关键

目录 前言 视觉AIGC的ChatGPT4.0时代 扩散模型的算力“饥渴症” 存内计算解救算力“饥渴症” 结语 前言 ​ 在这个AI技术日新月异的时代&#xff0c;我们正见证着前所未有的创新与变革。尤其是在视觉内容生成领域&#xff08;AIGC&#xff0c;Artificial Intelligence Generate…
阅读更多...
python导入非当前目录(如：父目录)下的内容

python导入非当前目录(如：父目录)下的内容

在开发python项目时&#xff0c;通常会划分不同的目录&#xff0c;甚至不同层级的目录&#xff0c;这时如果直接导入不在当前目录下的内容时&#xff0c;会报如下的错误&#xff1a;ModuleNotFoundError: No module named miniai其实这里跟操作系统的环境变量很类似的&#xff…
阅读更多...
less学习笔记

less学习笔记

一、什么是less&#xff1f; Less是CSS预处理语言&#xff0c;可以使用变量、嵌套、运算等&#xff0c;便于维护项目CSS样式代码。 二、less安装 使用npm包管理工具&#xff0c;全局安装less包 npm install -g lessless安装好的同时&#xff0c;lessc也安装好了 通过 lessc -…
阅读更多...
【图解IO与Netty系列】Netty核心组件解析

【图解IO与Netty系列】Netty核心组件解析

Netty核心组件解析 Bootstrap & ServerBootstrapEventLoop & EventLoopGroupChannelChannelHandler & ChannelPipeline & ChannelHandlerContextChannelHandlerChannelPipelineChannelHandlerContext ChannelFuture Bootstrap & ServerBootstrap Bootstra…
阅读更多...
代码随想录算法训练营第36期DAY56

代码随想录算法训练营第36期DAY56

DAY56 套磁很顺利&#xff0c;发现又有书读了&#xff01; 300最长递增子序列 朴素法&#xff0c;这个好想&#xff0c;但是不对&#xff0c;比如 0 1 0 3 2 3 我的算法会找出0 1 3作为答案&#xff0c;而不是0 1 2 3 可以看出&#xff0c;后面的状态依赖于前面的状态&am…
阅读更多...
ELK组件

ELK组件

资源列表 操作系统 IP 主机名 Centos7 192.168.10.51 node1 Centos7 192.168.10.52 node2 部署ELK日志分析系统 时间同步 chronyc sources -v 添加hosts解析 cat >> /etc/hosts << EOF 192.168.10.51 node1 192.168.10.52 node2 EOF 部署Elasticsea…
阅读更多...
Oracle10.2.0.1冷备迁移之_数据文件拷贝方式

Oracle10.2.0.1冷备迁移之_数据文件拷贝方式

由于阿里云机房要下架旧服务器&#xff0c;单位未购买整机迁移服务&#xff0c;且业务较老不兼容Oracle11g&#xff0c;所以新购买一台新服务器进行安装Oracle10.2.0.1 &#xff0c;后续再将数据迁移到新服务器上。 id 数据库版本 操作系统版本 实例名 源库 115.28.242.25…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023