本节介绍奈奎斯特稳定判据、对数稳定判据,并引入稳定裕度
本节介绍频率特性法分析系统性能
本节介绍通过开环频率特性得到闭环频率特性的方法
文章目录
- 频域稳定判据
- 奈奎斯特稳定判据
- Z = P − 2 N Z=P-2N Z=P−2N
- 奈奎斯特稳定判据的推导
- 对数稳定判据
- 容易判断出错的情况
- 临界稳定问题
- 相对稳定性分析
- 稳定裕度定义
- 计算
- 补充
- 分析系统性能
- 利用开环对数幅频特性分析系统性能
- 三频段理论
- 二阶系统
- 高阶系统
- 利用闭环频率特性分析系统性能
- 闭环频率特性
- 等M圆、等N圆
- 尼柯尔斯图线(Nichols)
- 闭环频域指标->时域指标
- 二阶系统
- 高阶系统
频域稳定判据
之前介绍过一个劳斯稳定性判据,属于代数稳定性判据。在不解出特征根的情况下可以判断系统的稳定性。但这种判据不能指导我们如何调整系统结构才能改善系统稳定性。
而这里讲到了系统的频域特性,也就相应的有两种频域稳定判据:奈奎斯特判据和对数稳定判据。对数稳定判据实际是奈氏判据的推广。
频域稳定判据可以由开环频率特性直接判断闭环系统的稳定性,而且可以研究如何调整系统结构参数来改善系统稳定性及性能的问题。
奈奎斯特稳定判据
系统的Nyquist图不穿过 ( − 1 + j 0 ) (-1+j0) (−1+j0)点,且逆时针包围 ( − 1 + j 0 ) (-1+j0) (−1+j0)点的圈数R = 开环传递函数在s右半平面的极点数P,则系统稳定。
再直观一点就是:
Z
=
P
−
R
Z=P-R
Z=P−R,如果Z=0,则系统稳定。
Z:在右半s平面中的闭环极点数。根据稳定的充要条件:全部闭环极点均均有负的实部,可知只有当Z=0时,系统才稳定。
注意这里的Nyquist图,
ω
\omega
ω取值是
(
−
∞
,
+
∞
)
(-\infty,+\infty)
(−∞,+∞)。负频率是由于fourier变换产生的,没有物理意义,所以一般画图画0到正无穷就可以了。但严格意义上来说,从负无穷到正无穷才是完整的Nyquist图。
对于
G
(
j
ω
)
G(j\omega)
G(jω),
ω
\omega
ω取+和-,幅值不变,而相角呈对称关系。很容易根据已经绘制好的Nyquist图画出另一半。
为了不用画这另一半,引入N:0到正无穷Nyquist曲线逆时针包围
(
−
1
+
j
0
)
(-1+j0)
(−1+j0)点的圈数,则有2N=R
因此有:
Z = P − 2 N Z=P-2N Z=P−2N
如果Z=0,则系统稳定。
先不管太多,根据这个式子,做一道题:
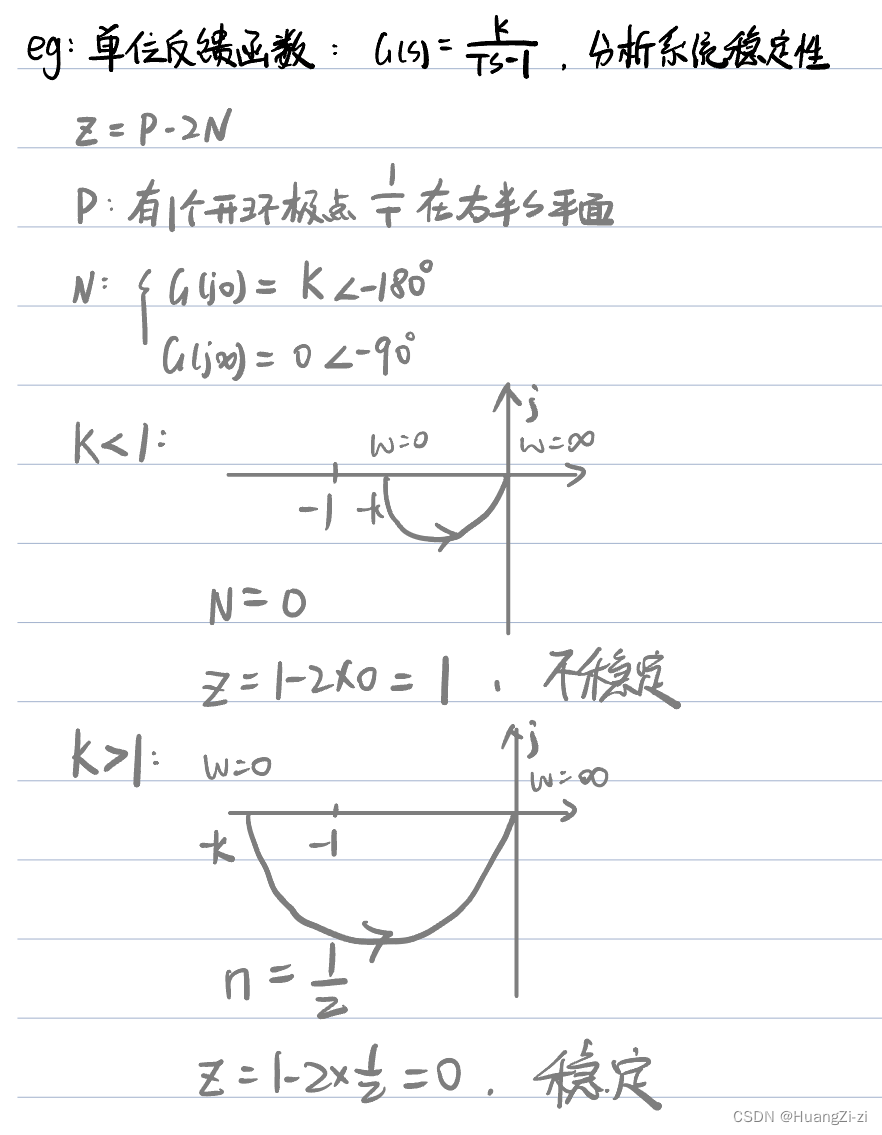
这个判据使用起来就是这样的。接下来进入理论升华:
奈奎斯特稳定判据的推导
幅角定理:S平面上,一条封闭曲线包围了F(s)的z个零点和p个极点,且该曲线不经过任意零极点。当s沿着这条封闭曲线顺时针旋转一周,对应F(s)向量绕原点顺时针旋转N=z-p周
奈氏路径:从
(
0
,
−
j
∞
)
(0,-j\infty)
(0,−j∞)沿虚轴到
(
0
,
+
j
∞
)
(0,+j\infty)
(0,+j∞),再经由半径无限大的圆弧回到
(
0
,
−
j
∞
)
(0,-j\infty)
(0,−j∞)的封闭曲线。如果在路径上有零点或者极点,则以一个半径无限小的圆弧从右边绕过。
运用幅角定理,沿奈氏路径,可以判断是否所有闭环极点都在s左半平面,进而判断稳定性。

零极点对应的角度:就是
(
s
−
p
i
)
(s-p_i)
(s−pi)和
(
s
−
z
j
)
(s-z_j)
(s−zj)在s环绕奈氏路径一周过程中角度的变化量。
F
(
j
ω
)
\bold{F(j\omega)}
F(jω)绕原点的角度:
∠
F
(
j
ω
)
=
∠
Π
(
s
−
z
i
)
Π
(
s
−
p
j
)
=
∑
∠
(
s
−
z
i
)
−
∑
∠
(
s
−
p
j
)
\angle F(j\omega)=\angle \frac{\Pi(s-z_i)}{\Pi(s-p_j)}=\sum\angle(s-z _i)-\sum\angle(s-p_j)
∠F(jω)=∠Π(s−pj)Π(s−zi)=∑∠(s−zi)−∑∠(s−pj)。代入零极点对应的角度就可以计算
F
(
j
ω
)
F(j\omega)
F(jω)转过的角度。(角度以逆时针为+)
系统稳定的条件:右半平面内系统闭环极点数量为0,也就是右半平面内F(s)零点数量为0,即Z=0。
F
(
j
ω
)
=
1
+
G
(
j
ω
)
H
(
j
ω
)
F(j\omega)=1+G(j\omega)H(j\omega)
F(jω)=1+G(jω)H(jω),因此
G
(
j
ω
)
H
(
j
ω
)
=
F
(
j
ω
)
−
1
G(j\omega)H(j\omega)=F(j\omega)-1
G(jω)H(jω)=F(jω)−1。F绕原点旋转,则GH绕(-1,j0)点旋转。
GH为开环传递函数。沿奈氏路径从
(
0
,
−
j
∞
)
(0,-j\infty)
(0,−j∞)沿虚轴到
(
0
,
+
j
∞
)
(0,+j\infty)
(0,+j∞)这一段GH的运动轨迹即为Nyquist图。从半径无穷大圆弧返回
(
0
,
−
j
∞
)
(0,-j\infty)
(0,−j∞)这一段GH为原点或实轴上的一点,不影响其围绕(-1,j0)的情况。
因此可以通过Nyquist图围绕(-1,j0)的情况计算Z=P-R,由于只画了一半,所以有Z=P-2N,当Z=0时系统稳定。
再来看一个例题:
这道题就是在虚轴上有零极点,奈氏路径需要绕过去的这个情况:
奈氏路径以无穷小的半径绕过一个点,对应Nyquist图以无穷大的半径围绕原点(方向、角度需要根据绕过点的性质判定)

怎么看幅相曲线环绕(-1,j0)点的圈数呢,可以想象自己站在(-1,j0)点上,从
ω
=
0
\omega=0
ω=0开始,眼睛盯着
G
(
j
ω
)
G(j\omega)
G(jω)点,身体跟着转动,直到
ω
=
+
∞
\omega=+\infty
ω=+∞,看看自己的身体转了几圈。
对数稳定判据
即通过对数频率特性计算N。因为幅相特性曲线还是不太好画的,而对数频率特性曲线就简单多了。所以希望可以在Bode图里面计算奈奎斯特稳定判据。
N
=
N
+
−
N
−
N=N^+-N^-
N=N+−N−
N+:正穿越次数
N–:负穿越次数
穿越:在
∣
G
(
j
ω
)
∣
>
1
|G(j\omega)|>1
∣G(jω)∣>1的范围中,
φ
(
j
ω
)
\varphi(j\omega)
φ(jω)穿越-180
°
\degree
°,从上往下穿叫负穿越,从下往上穿叫正穿越。
以-180
°
\degree
°为渐近线的,算半次穿越,在-180以上为正,-180以下为-
∣
G
(
j
ω
)
∣
>
1
|G(j\omega)|>1
∣G(jω)∣>1,也就是
L
(
ω
)
>
0
L(\omega)>0
L(ω)>0,截止频率以上。
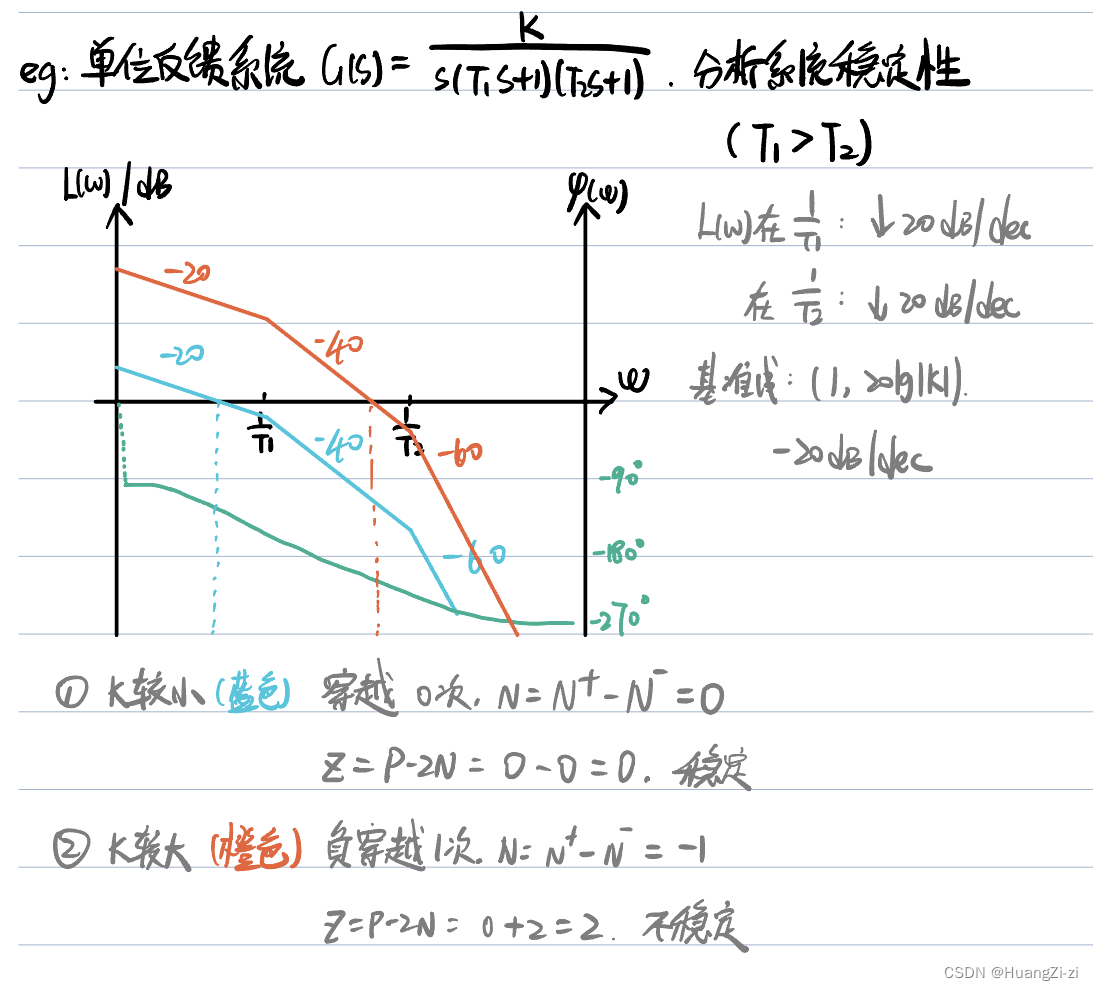
同一道例题,如果画对数频率特性,就会更加简单直观,也不用我们去转圈了。
再看一个以-180
°
\degree
°为渐近线的情况:
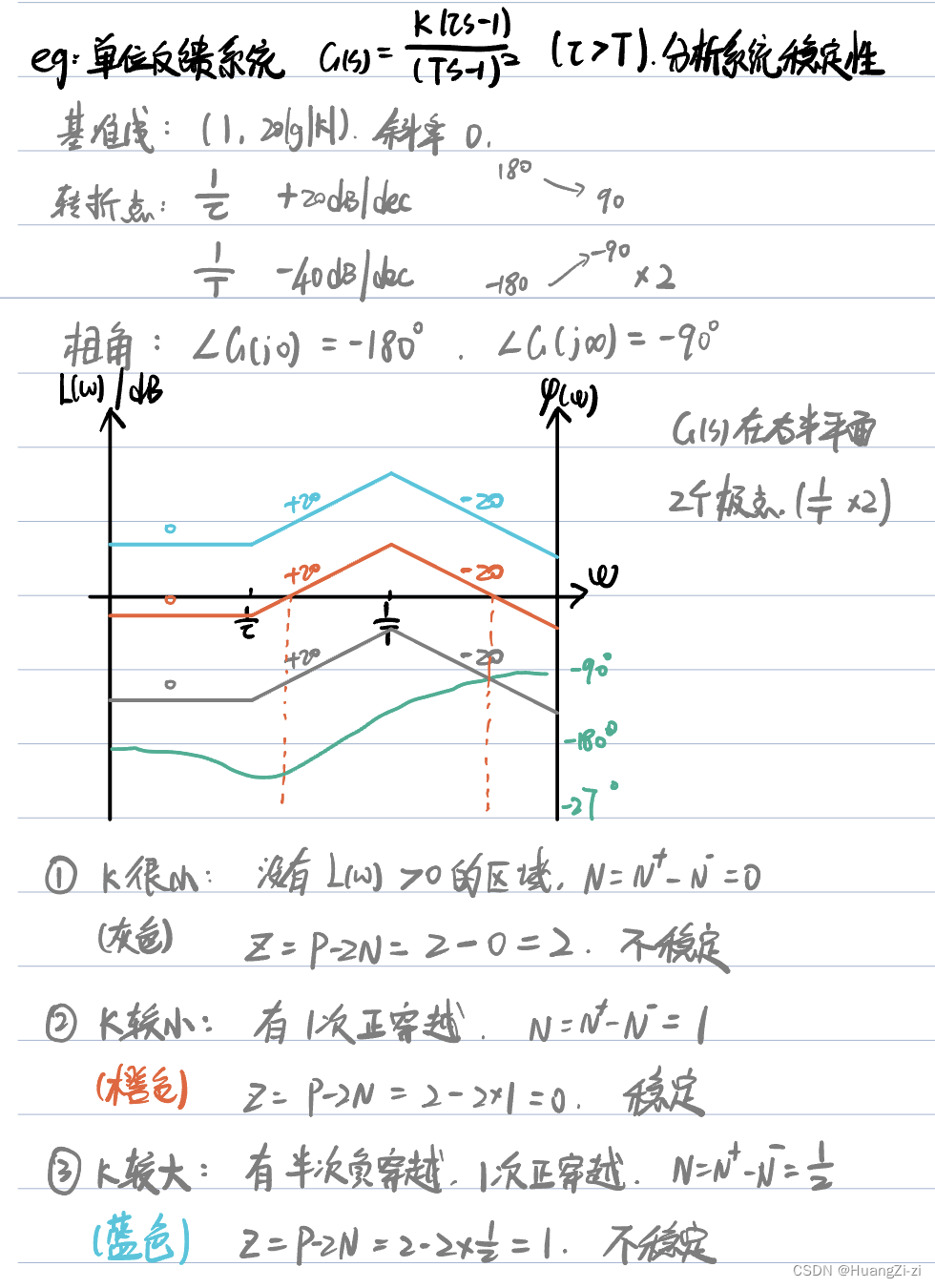
容易判断出错的情况
问题在于我们画的折线Bode图,是一个渐近的折线,所以有时候会出一些问题:
幅值相关问题
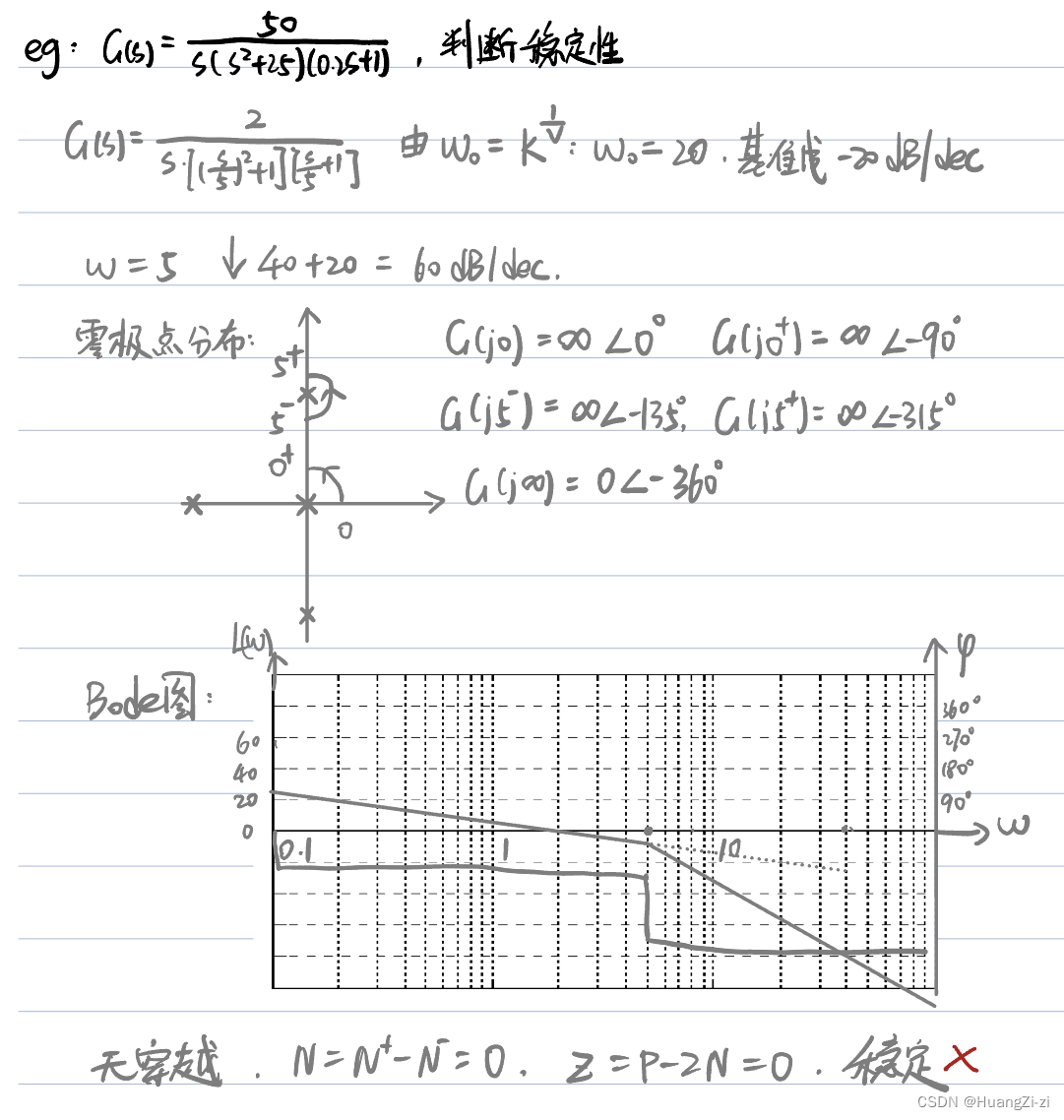
如果这么做就会得到系统稳定的结论。但如果画根轨迹,或者画幅相特性曲线都会发现系统实际是不稳定的。
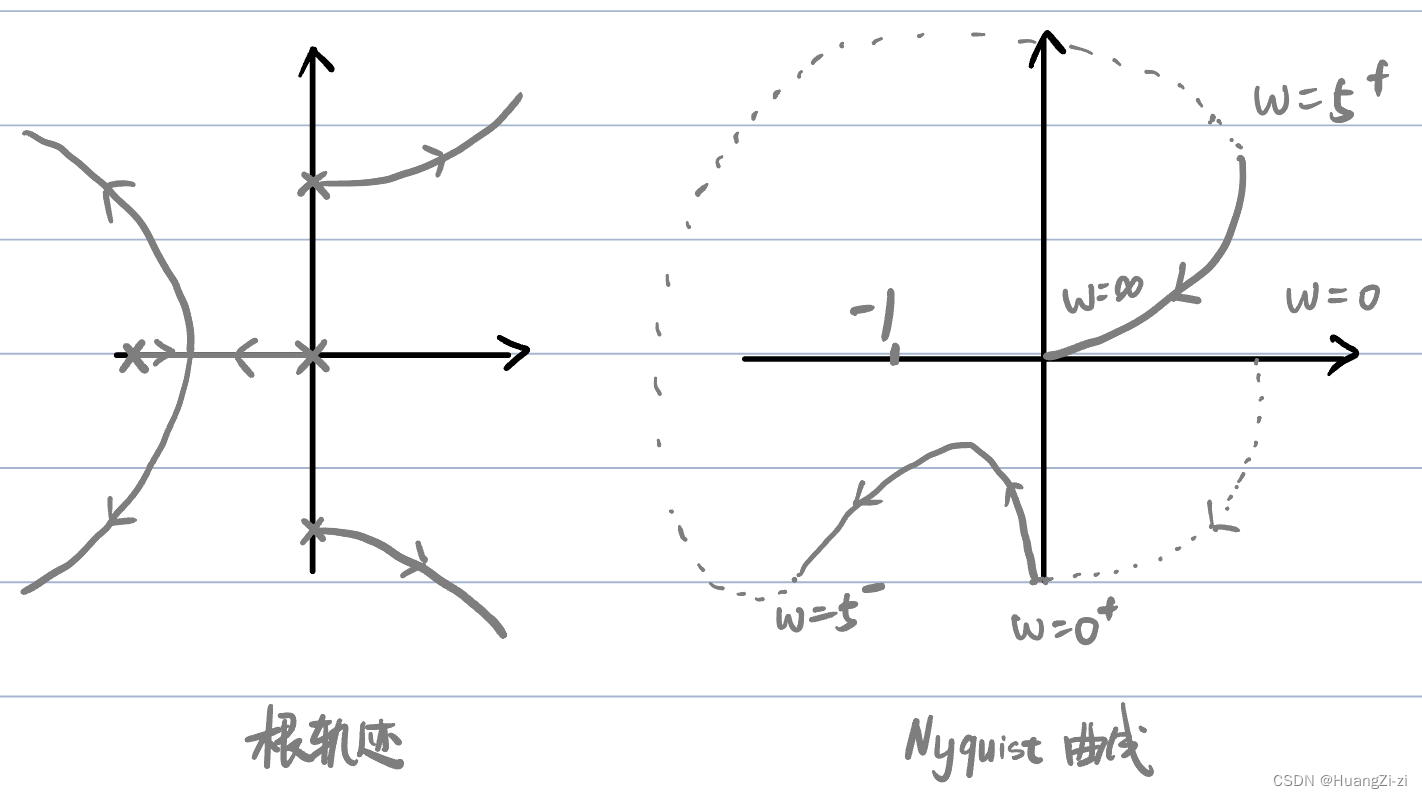
尤其是看幅相曲线,一定是包围(-1,j0)点-1圈的,N不应该为0。
这道题的问题就在于Bode图过于近似了。在
ω
=
5
\omega=5
ω=5附近,幅值应该是无穷大。
修正对数幅相特性后:
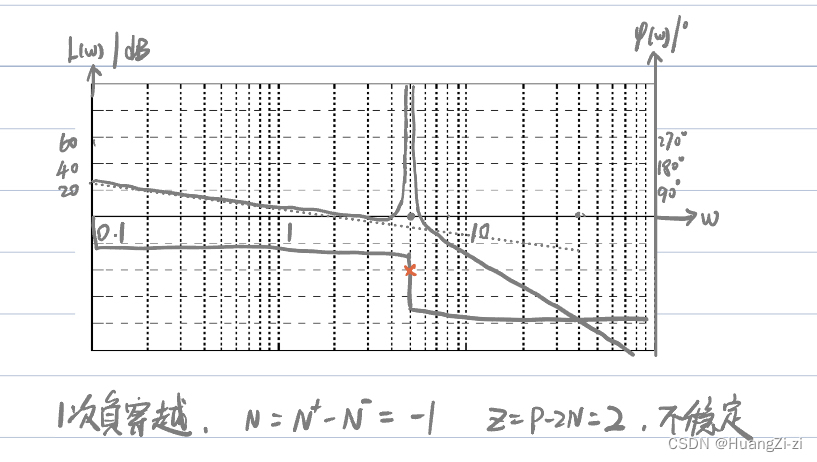
相角相关问题
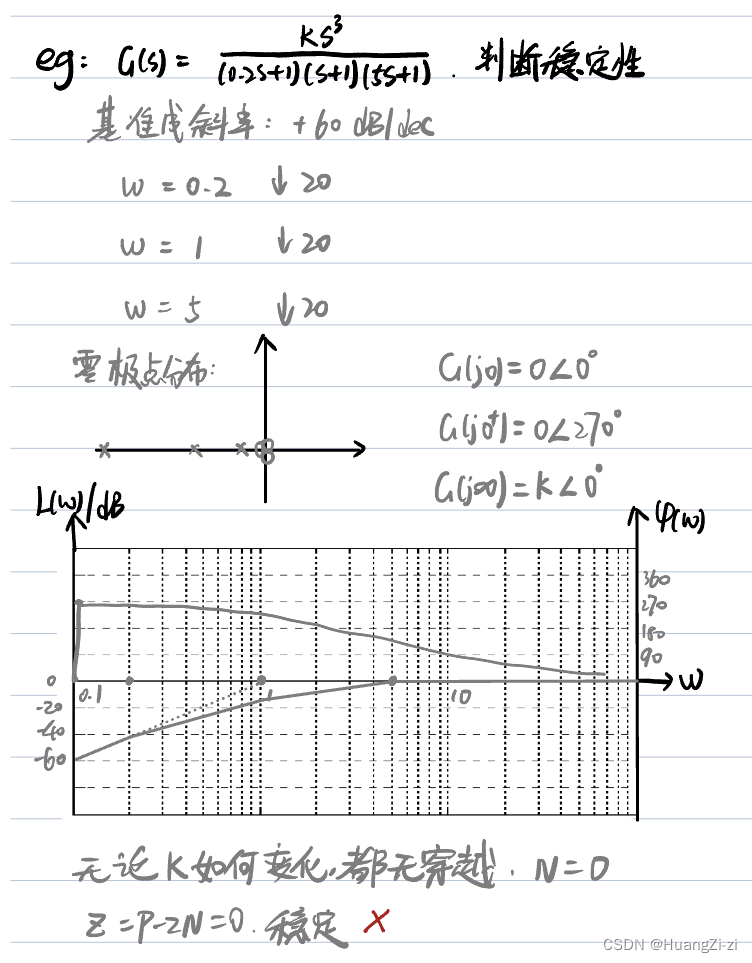
看起来没有发生穿越,但问题在于穿越-180和穿越+180没有本质区别(因为+180和-180是同样的方向)依次类推,穿越±360、±540、等等都相当于穿越-180
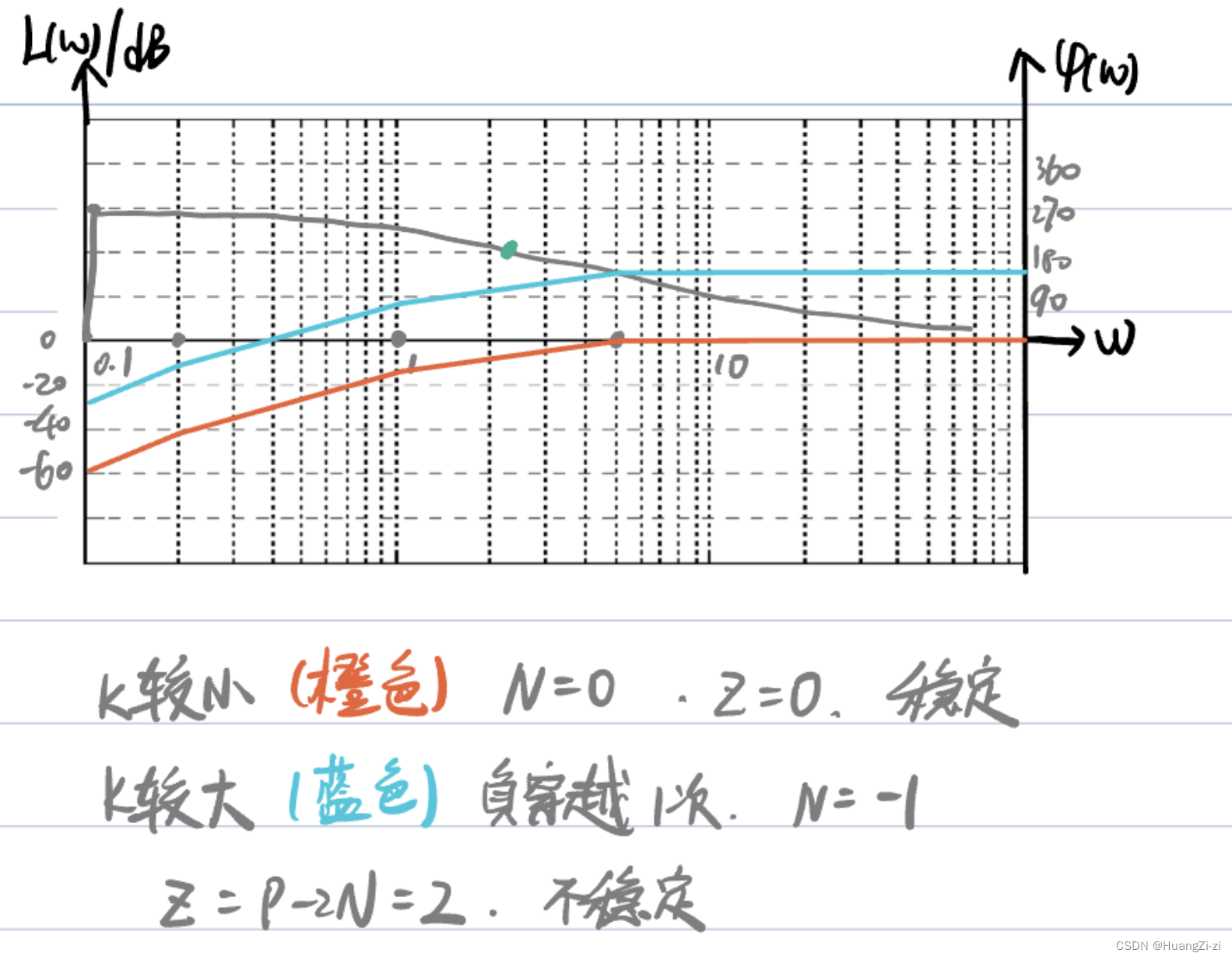
穿越180的整数倍时,同样是从上到下为负穿越,反之为正穿越。
画根轨迹和幅相特性同样可以验证:
临界稳定问题
之前的讨论都是稳定或者不稳定,而临界稳定问题被单独拿出来了。
临界稳定状态:幅相特性曲线过(-1,j0)点。这个很好判别,只需要计算幅相特性曲线和实轴的交点就可以了,不再过多讨论。
相对稳定性分析
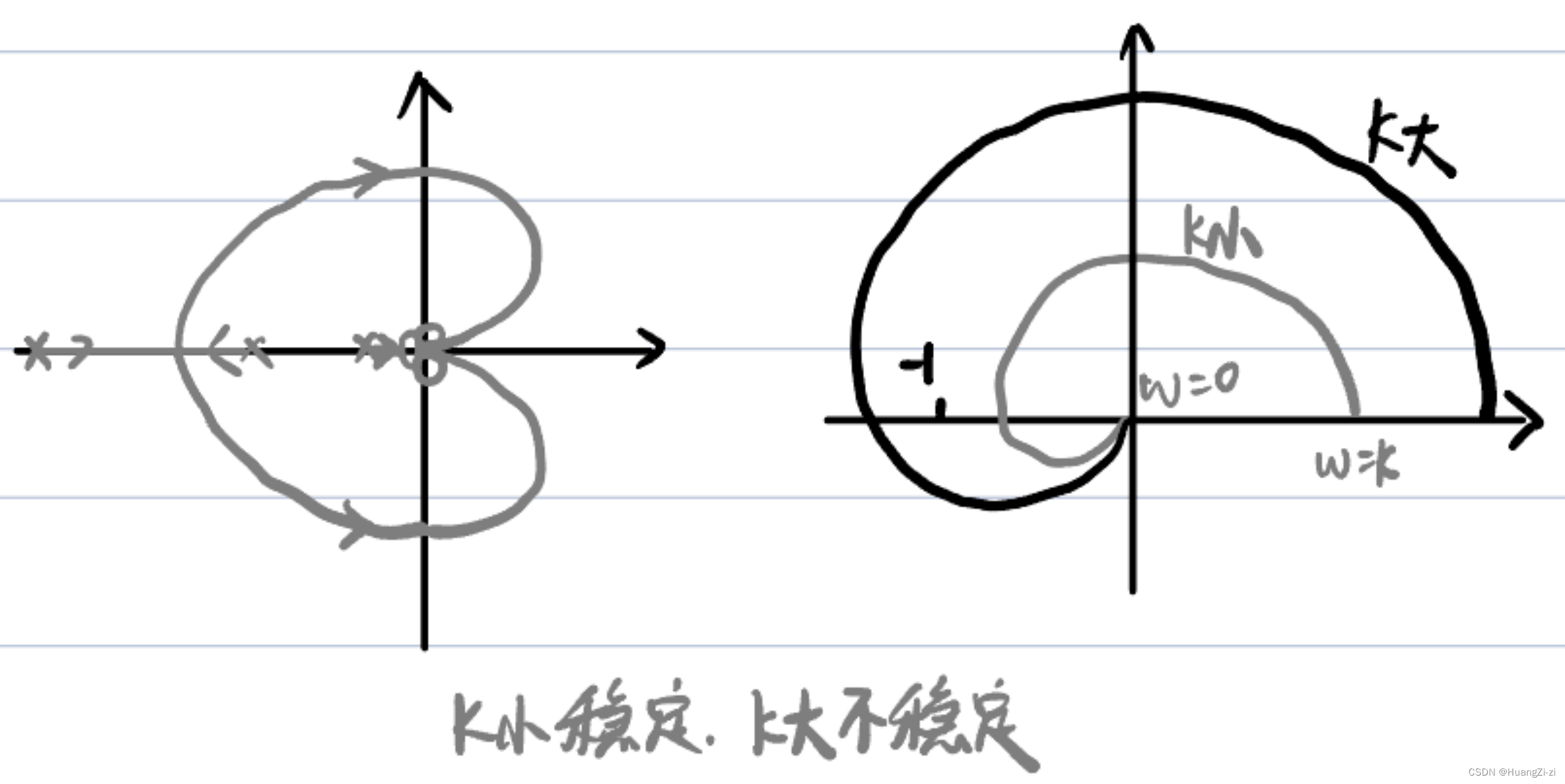
相对稳定性,指除了在正常条件下系统稳定,还要求系统具有一定的“富余”,也就是某一参数或特性在一定范围内波动,系统仍然保持稳定。
在频域稳定判据里面,有一个非常重要的点(-1,j0),这个点为临界点。幅相特性曲线距离临界点的远近,反映了系统的相对稳定性。离临界点越远,相对稳定性越好。
而稳定裕度是用来度量频域相对稳定性的。(开环频率指标之一)
稳定裕度定义
相角裕度 γ \gamma γ
γ
=
180
°
+
∠
G
(
j
ω
c
)
\gamma=180\degree+\angle G(j\omega_c)
γ=180°+∠G(jωc)
其中
ω
c
\omega_c
ωc为截止频率
幅值裕度h
h
=
1
∣
G
(
j
ω
g
)
∣
\displaystyle h=\frac{1}{|G(j\omega_g)|}
h=∣G(jωg)∣1
其中
ω
g
\omega_g
ωg为相角交界频率,也就是相角为
−
180
°
-180\degree
−180°时的频率
几何意义
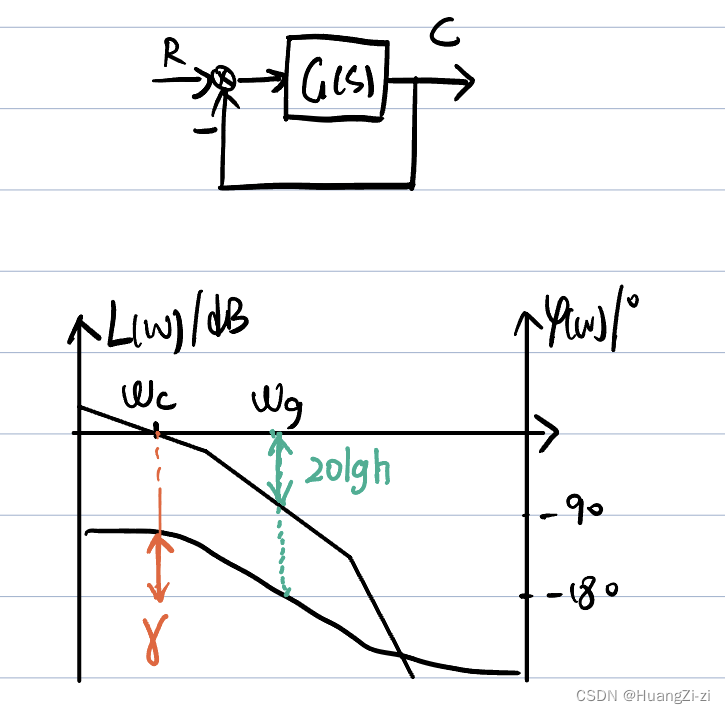
如图所示。一般要求:
{
γ
>
40
°
h
>
2
\left \{\begin{aligned} \gamma&>40\degree\\ h&>2 \end{aligned}\right.
{γh>40°>2
物理意义
相角裕度:系统在相角方面的稳定储备量
原本稳定的系统,但增加延迟环节改变相角之后,就可能变得不稳定了。
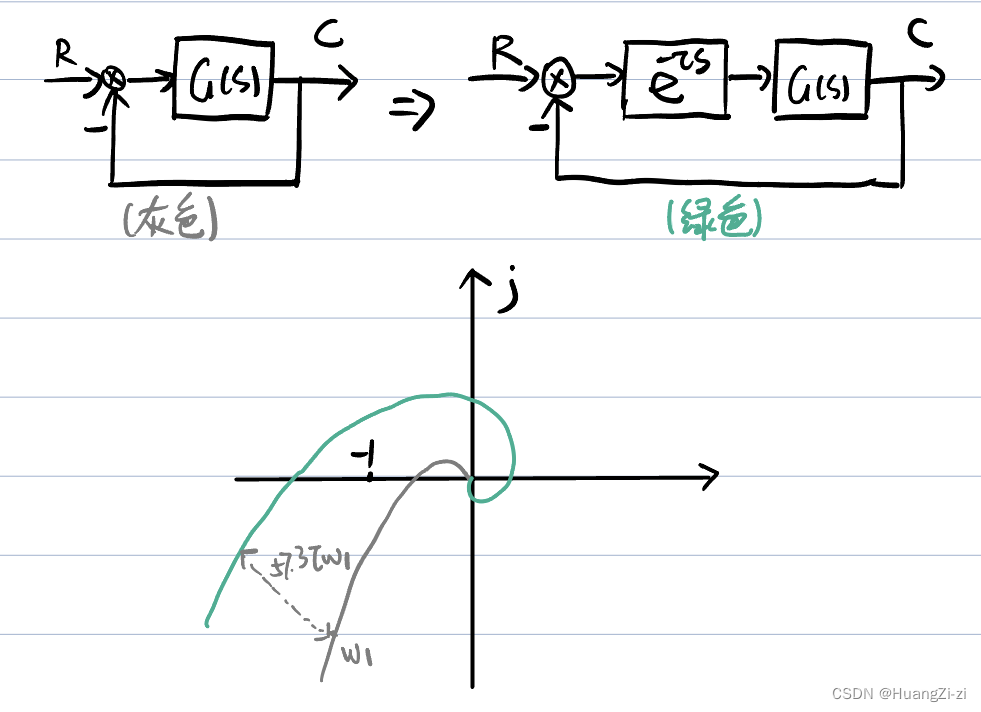
「注:增加一个纯延时环节相角滞后57.3 ° \degree °,在本文之前的推导中写的是 180 ° π \frac{180\degree}{\pi} π180°」
幅值裕度:系统在幅值方面的稳定储备量
原本稳定的系统,增大增益后可能就不稳定了。
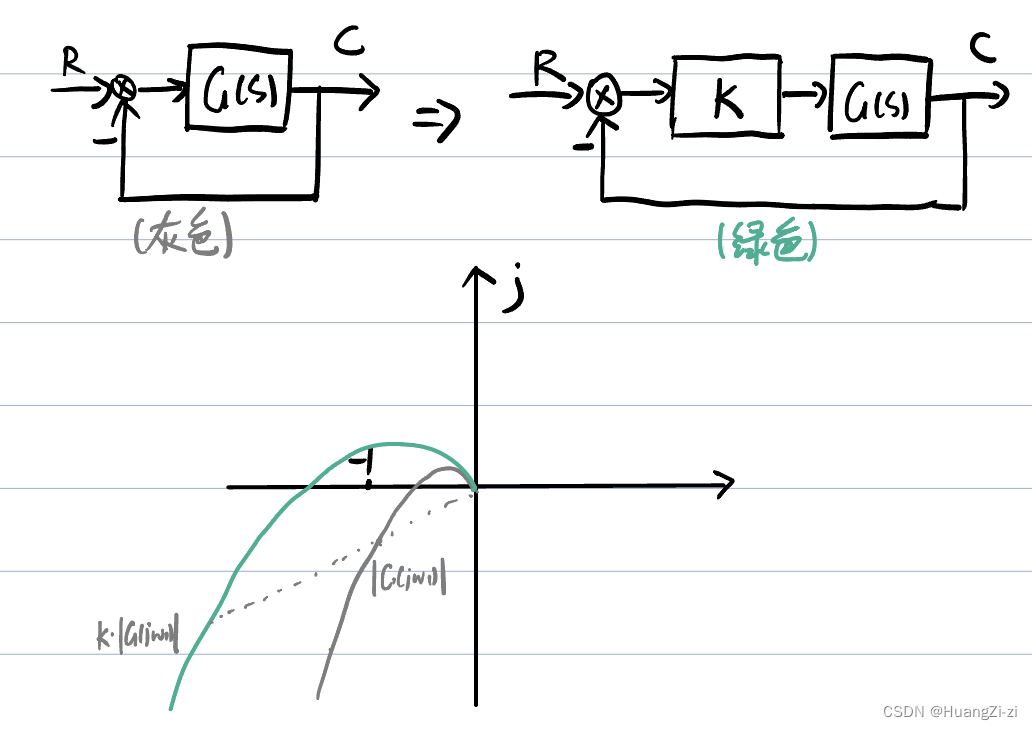
计算
根据定义解根

没什么好说的,就是硬算,非常不推荐这种做法,因为太麻烦了。
稍微简单一点的方法是,通过计算幅相特性曲线与实轴的交点来确定
ω
g
\omega_g
ωg,可以规避三角函数运算。
即把
G
(
j
ω
)
G(j\omega)
G(jω)写成
X
+
j
Y
X+jY
X+jY的形式,令虚部
Y
Y
Y=0,即可求出
ω
g
\omega_g
ωg(计算方法在开环幅相特性曲线的部分有举例)
根据Bode图读根
计算截止频率的时候,直接按照渐近的方法算,能快速很多。稍微有一点误差,但一般在接受范围内。

这里解释一下为什么对于 20-40-60 斜率的Bode图有
ω
g
=
ω
1
ω
2
\omega_g=\sqrt{\omega_1\omega_2}
ωg=ω1ω2:
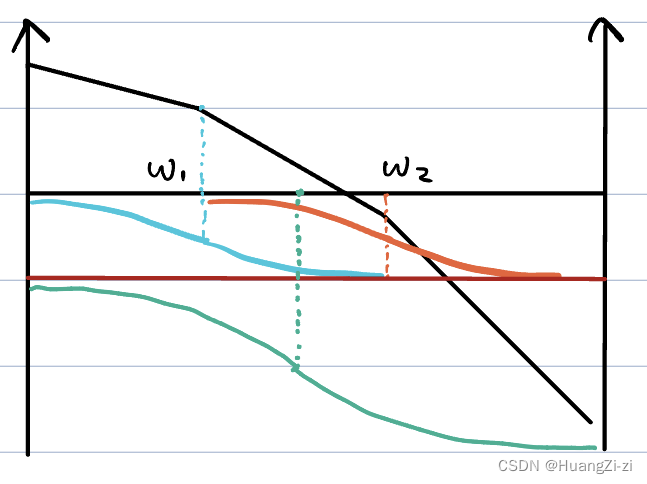
20-40-60斜率,就可以知道是一个1型系统,有两个拐点,都是惯性环节。之前推证过惯性环节相频特性是中心对称的,所以根据对称性叠加(蓝、橙、红),可知在两个惯性环节中点处刚好叠加出-180(绿)。计算中点: ω g = ω 1 ω 2 \omega_g=\sqrt{\omega_1\omega_2} ωg=ω1ω2——等距等比
补充
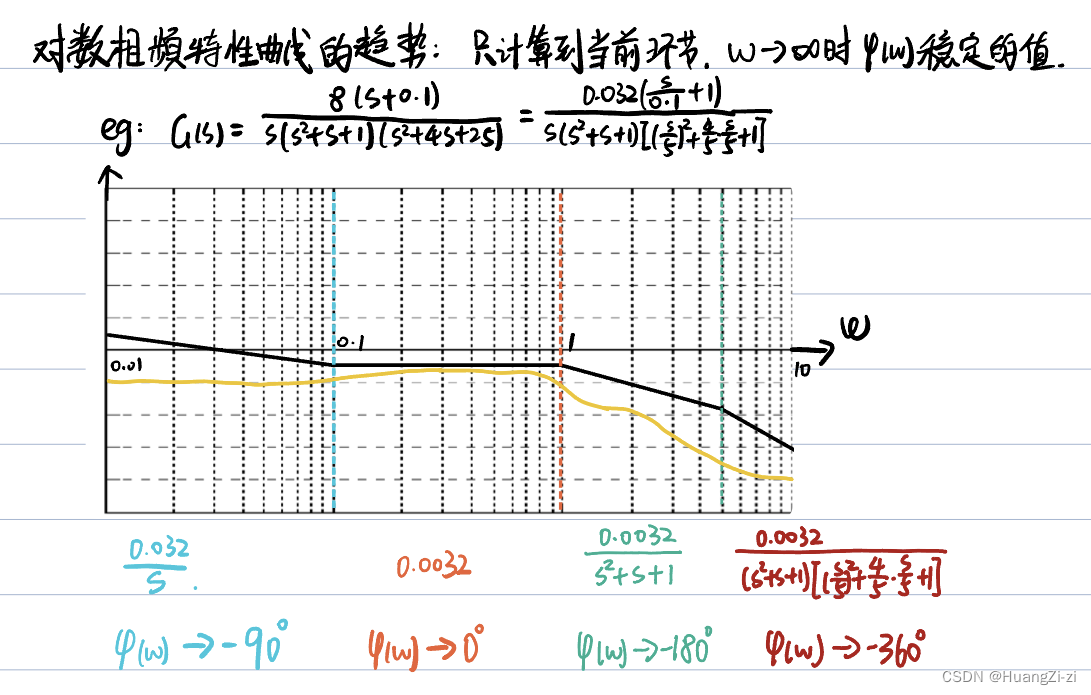
也就是说,在每一段上,相频曲线都有一个趋势。根据这个趋势可以粗略估算相角裕度:

而由于趋势不能真正达到,所以具体不是是稳定还需要看这一段前后的影响。
分析系统性能
利用开环对数幅频特性分析系统性能
三频段理论
首先注意,这里的低频中频高频并不是在信号领域定义的高中低频。对于控制系统而言,一般工作频率几~几百赫兹,高中低是基于控制系统划分的。

低频段反映系统稳态误差。由静态误差系数法可知,系统型别高,开环增益高,相对来说稳态误差更小。也就是低频段曲线应该陡、高。
高频段反映系统抗高频噪声的能力。欲使噪声影响小,应使高频段曲线矮。
中频段是本节着重讨论的内容:

接下来找
ω
c
、
γ
\omega_c、\gamma
ωc、γ和
σ
%
、
t
s
\sigma\%、t_s
σ%、ts的关系:
二阶系统

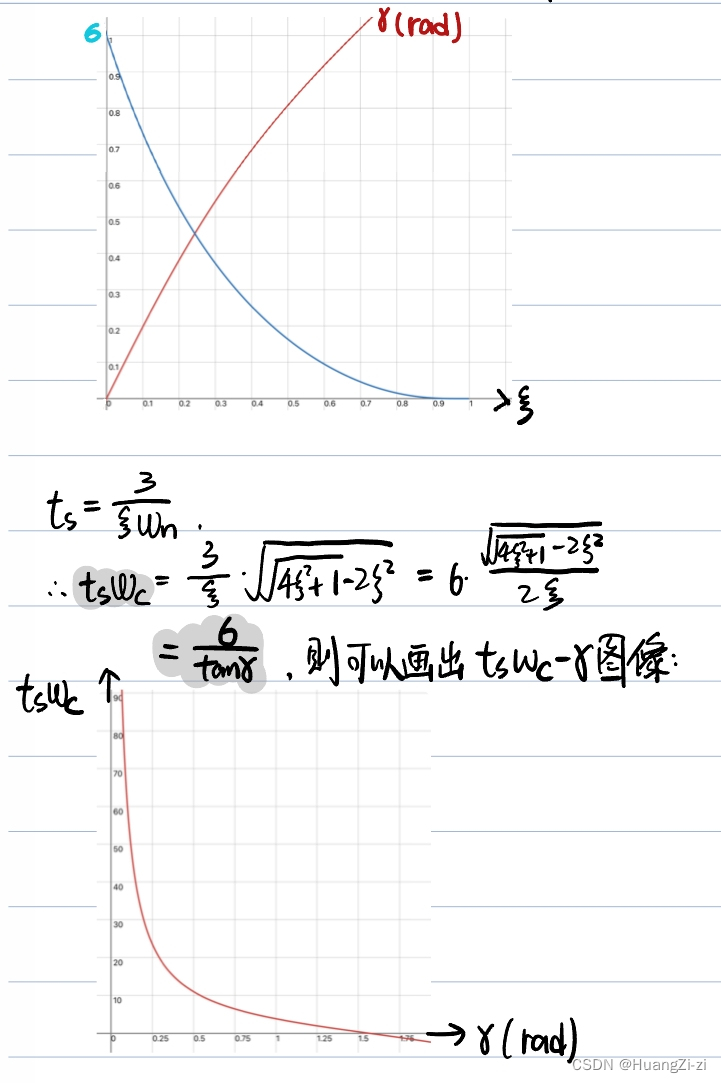
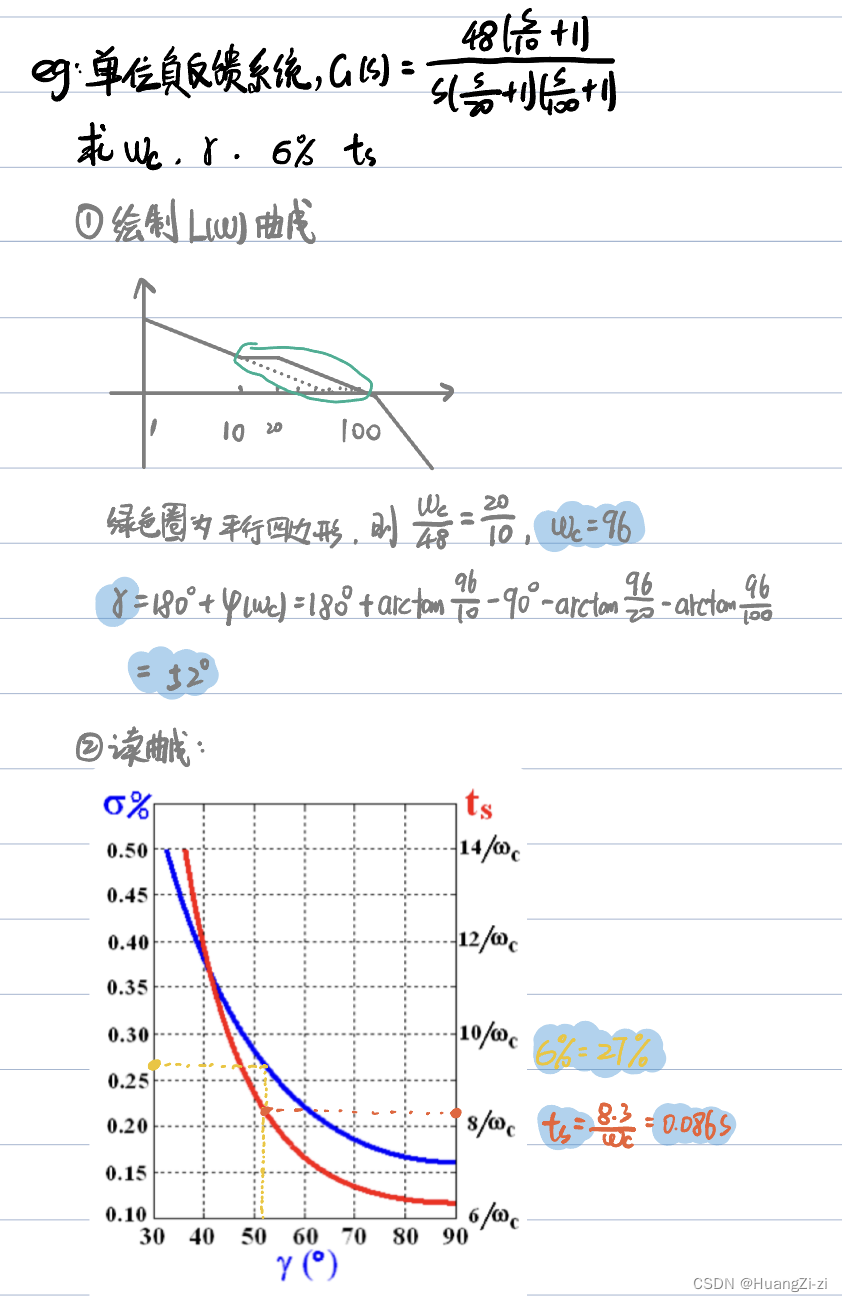
解题的时候根据
L
(
ω
)
L(\omega)
L(ω)曲线,计算
ω
c
、
γ
\omega_c、\gamma
ωc、γ,再到两幅图里面读出相应的性能参数即可。
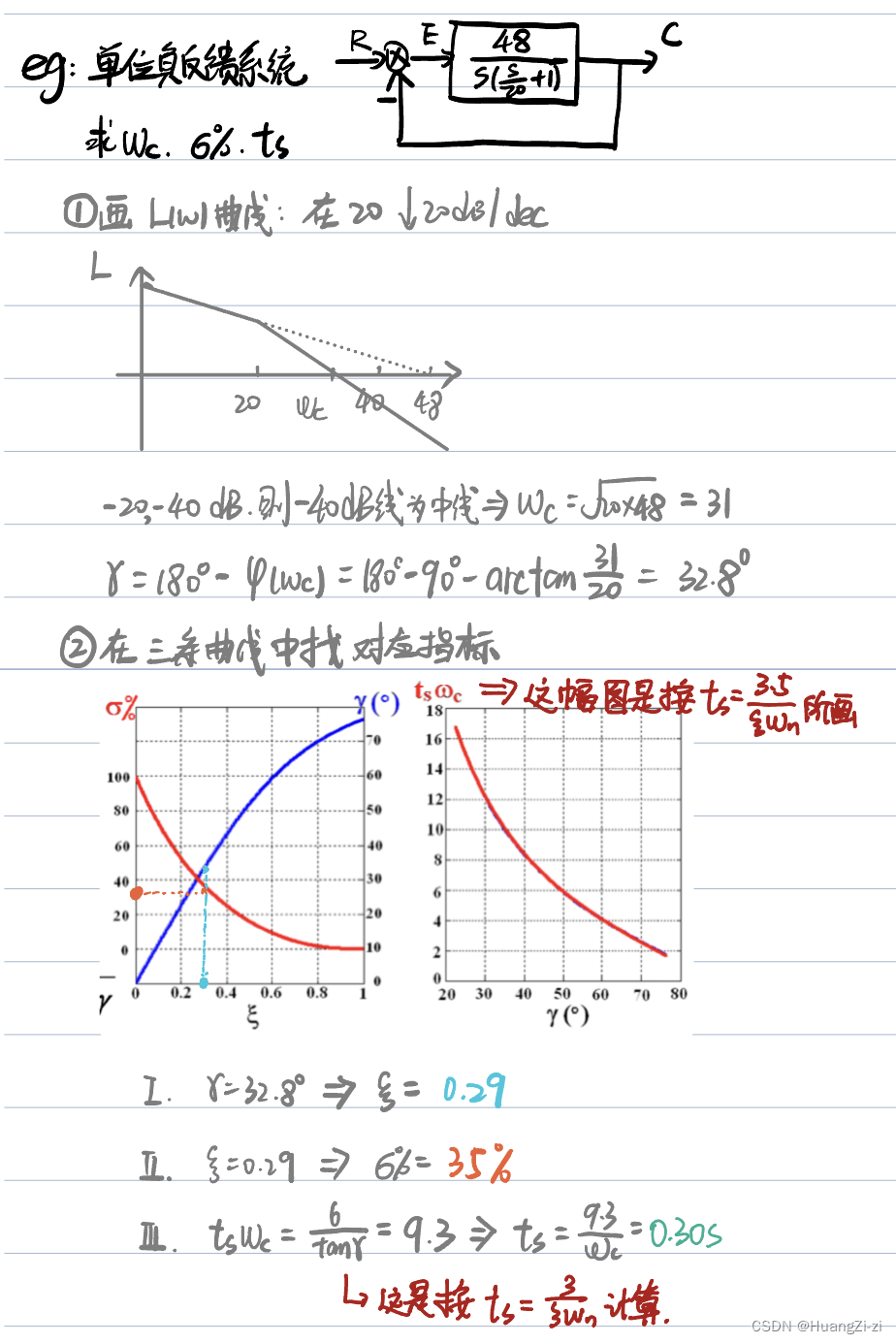
「曲线图源:卢京潮课件」
高阶系统
推导略。对于高阶系统有近似表达式,同样反映
ω
c
、
γ
\omega_c、\gamma
ωc、γ和
σ
%
、
t
s
\sigma\%、t_s
σ%、ts的关系:
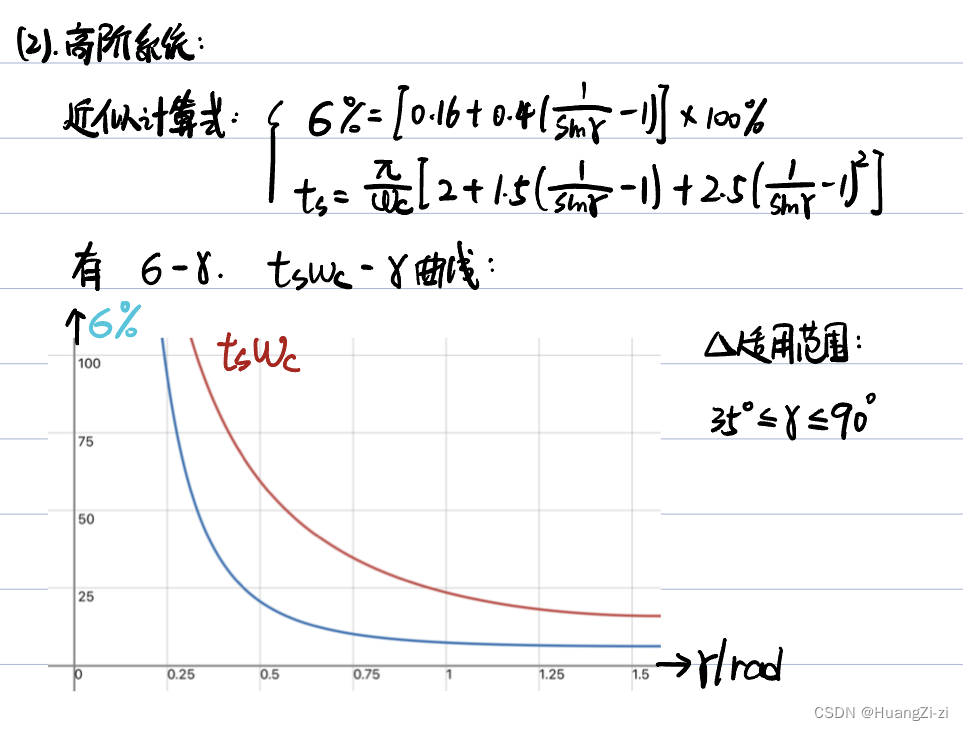
其实也不一定必须读图,也可以带进式子里计算。
「曲线图源:卢京潮课件」
利用闭环频率特性分析系统性能
虽然可以通过开环特性分析闭环性能,但是由于可以通过实验轻松得到系统的闭环频率特性,且闭环频率特性的一些特征量在工程应用中十分广泛,所以研究闭环频率特性还是很有必要的。
闭环频率特性
特征量:

向量法研究
也就是从定义着手
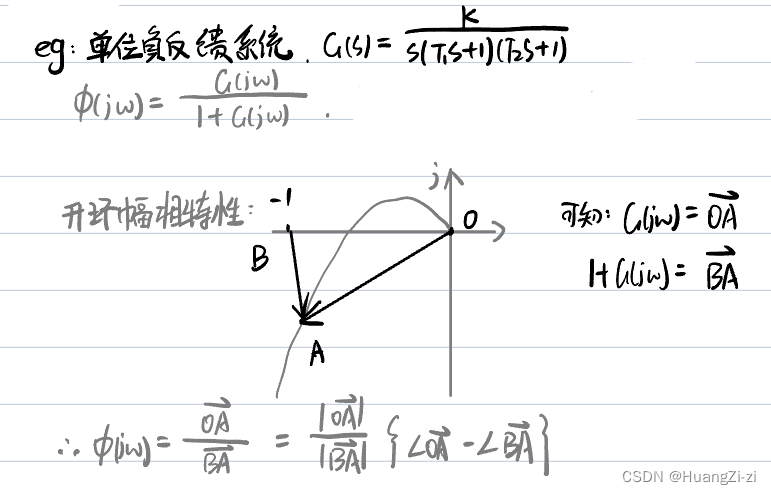
这样就从几何层面建立了开环特性和闭环特性的关系,知道了开环幅相特性曲线,就可以得出闭环的频率特性了
等M圆、等N圆
但是每次画图,求长度算角度比较复杂,也不容易看出趋势,所以又引入了两个辅助工具:
等M圆

「曲线图:卢京潮课件」
等N圆
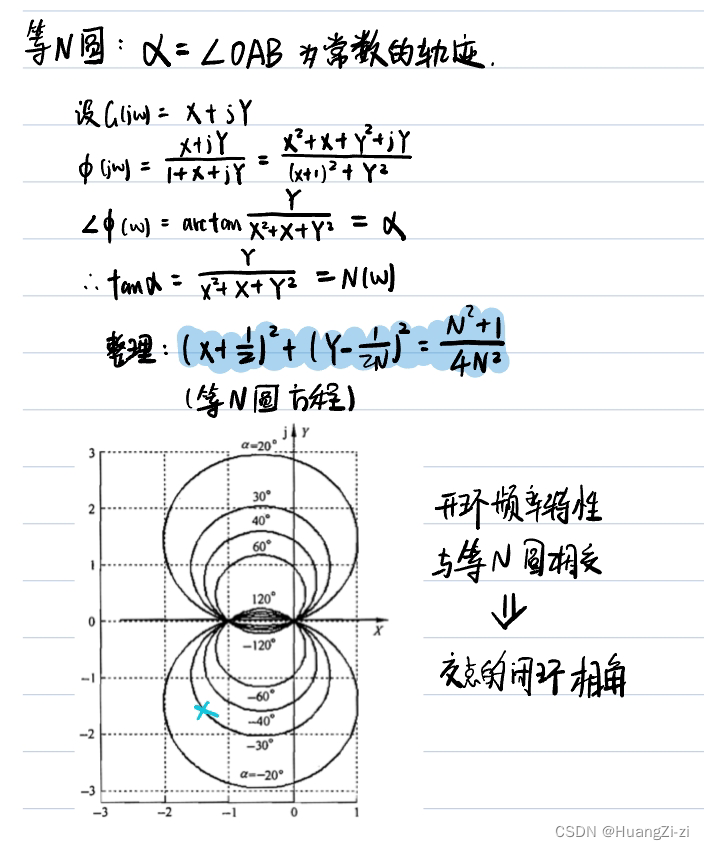
「曲线图:卢京潮课件」
在等M圆和等N圆就像是地图里的等高线一样。在这幅"地图"里面画出开环Nyquist,就能根据交点,确定某一个
ω
\omega
ω下的闭环幅值和相角。
尼柯尔斯图线(Nichols)
首先注意这里说的是Nichols图线,而不是Nicholes图。(他们的关系就像是尺子和地图一样,图线是用来读取图上的数据用的)
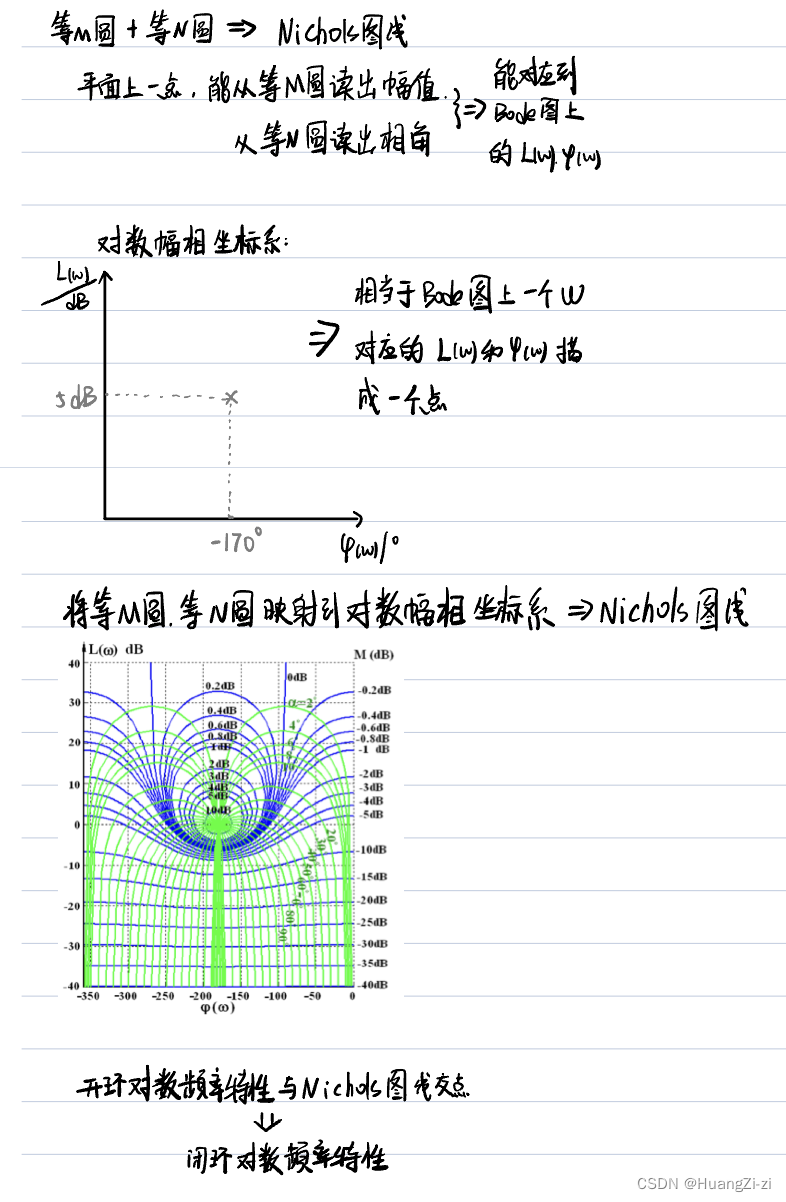
「曲线图:卢京潮课件,蓝色为对数幅值,绿色为相角」
尼柯尔斯图线其实本质上就是等M圆、等N圆映射到对数幅相座标系时的曲线。
闭环频域指标->时域指标
二阶系统
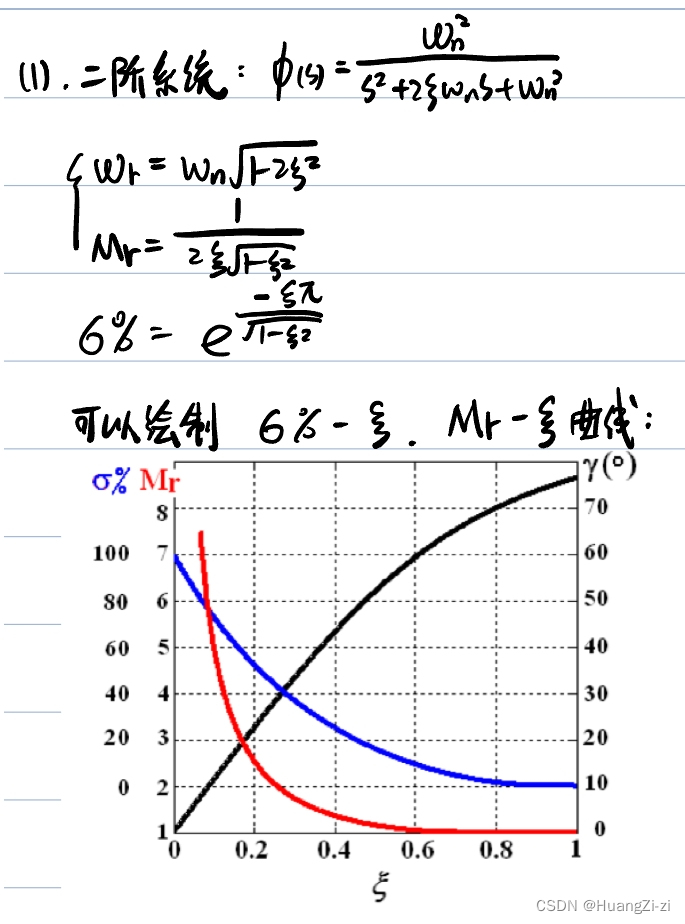
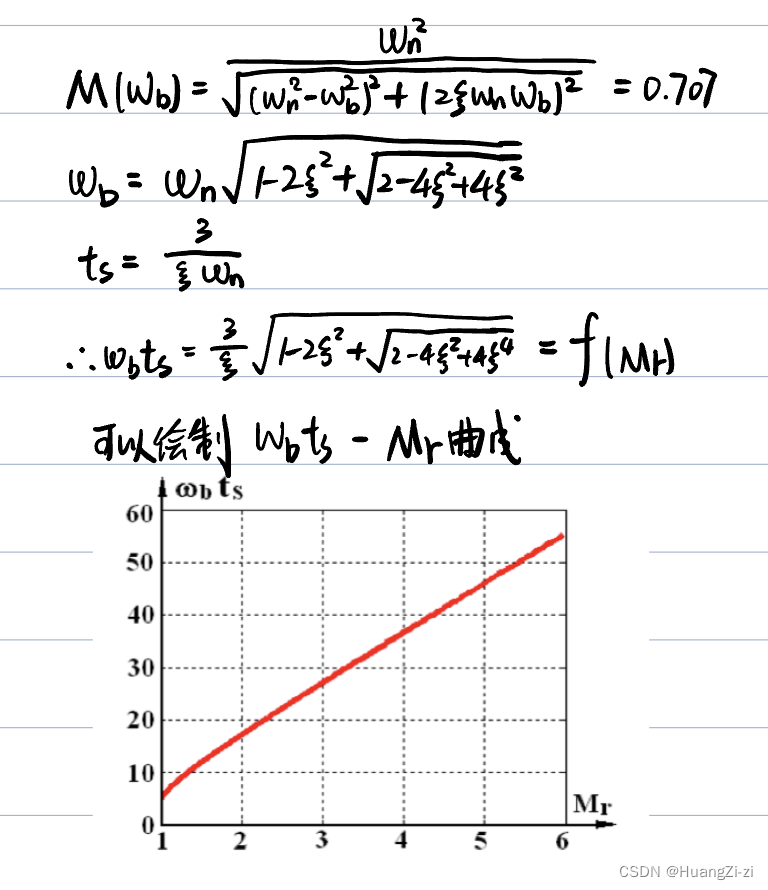
「曲线图:卢京潮课件」
跟之前利用开环频率特性分析性能的时候一样,首先找出带宽频率
ω
b
\omega_b
ωb,通过这个频率读出阻尼系数
ξ
\xi
ξ和超调量
σ
\sigma
σ,计算谐振峰值在代入曲线求调节时间
t
s
t_s
ts
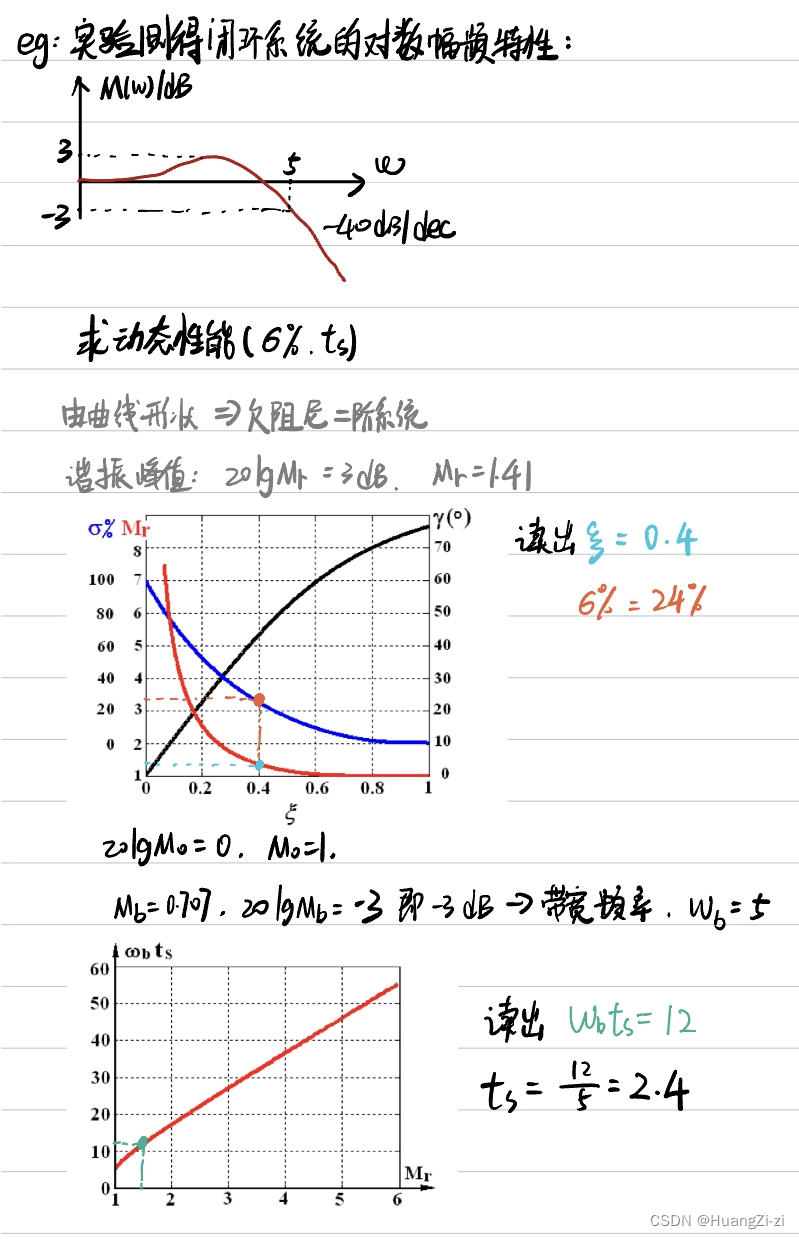
高阶系统
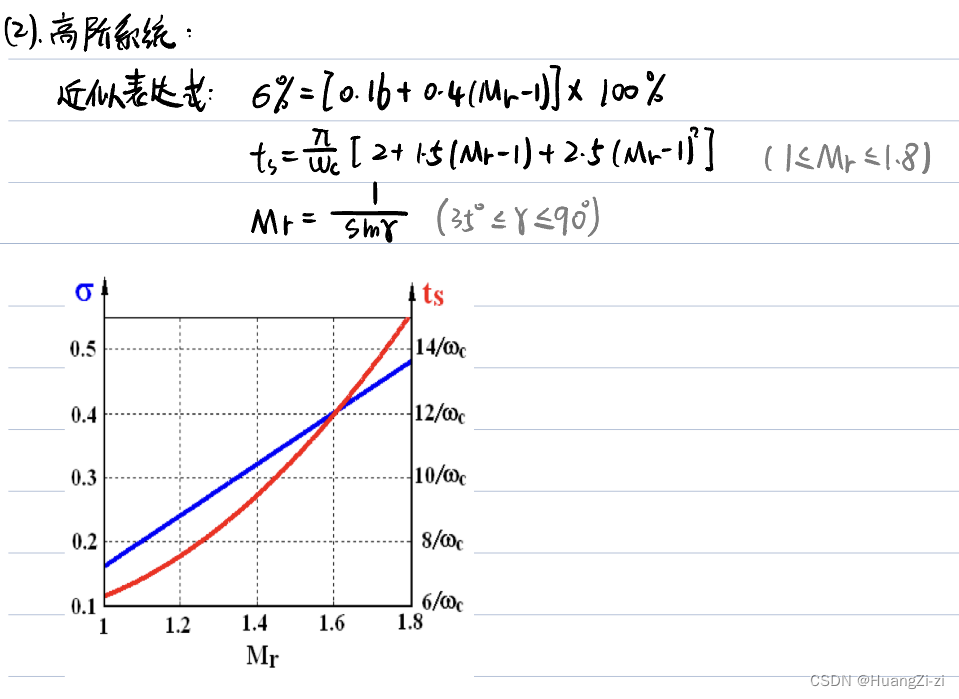
跟之前开环的情况是一样的,依然是画曲线,再读点。
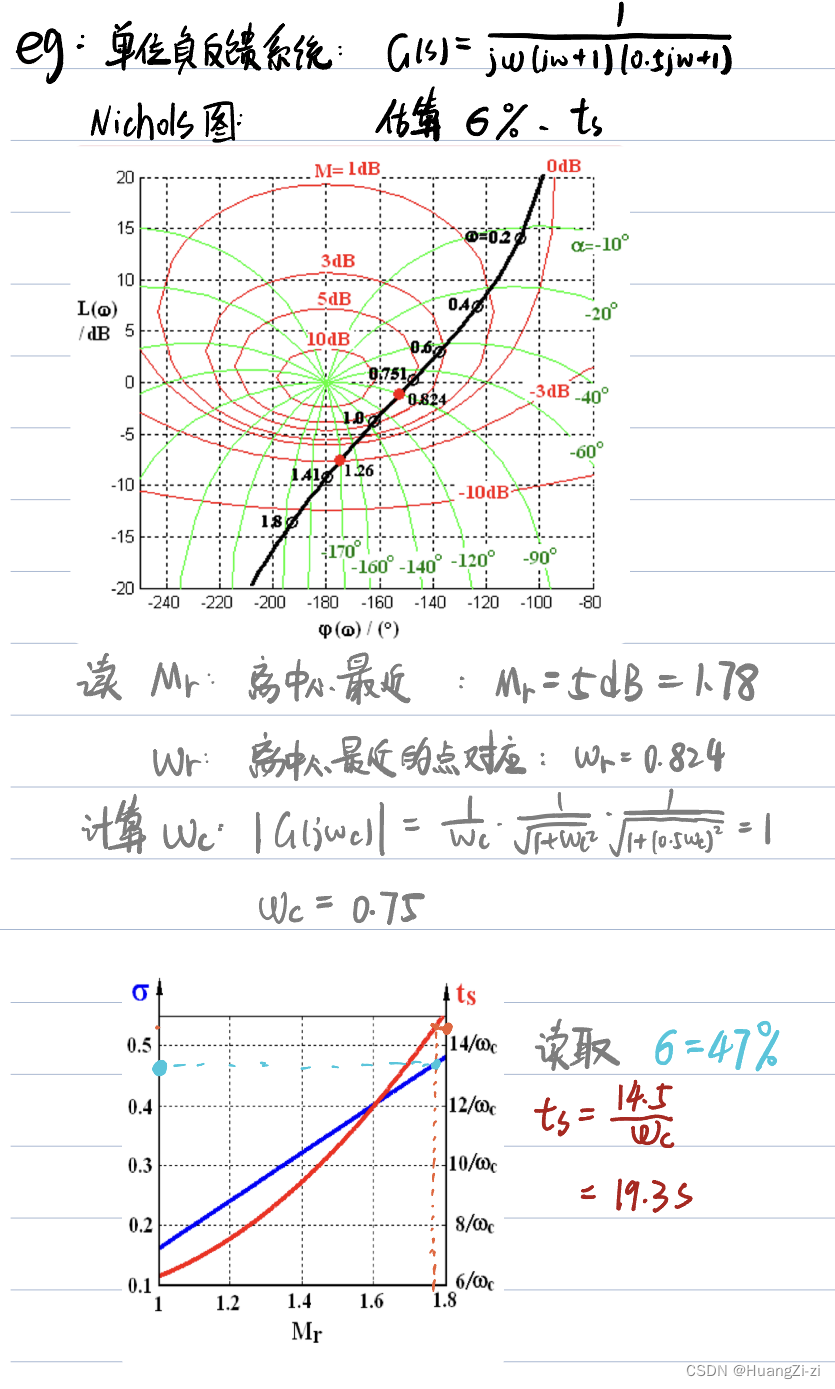
利用开环频率分析性能与利用闭环频率特性分析性能,达到的目的是一样的,两种方法根据方便选用即可。





![流批一体计算引擎-8-[Flink]的Table API连接器](https://img-blog.csdnimg.cn/4faf4c0a472e405d9c3edac3d11ebc85.png)