文章目录

前言
一、数论
- 例题
- - 例题1：AcWing 1246. 等差数列（最大公约数，第十届蓝桥杯省赛C++B第7题）
  - - 分析
    - 题解：最大公约数
  - 例题2：AcWing 1295. X的因子链（算数基本定理、欧拉筛选，多重集合排列数）
  - - 分析
    - 题解：数论-算数基本定理、欧拉筛选，多重集合排列数
  - 例题3：AcWing 1296. 聪明的燕姿
  - - 分析
    - 题解：欧拉筛+约数之和(dfs)+剪枝
  - 例题4：AcWing 1299. 五指山（扩展欧几里得）
  - - 分析
    - 题解：扩展欧几里得
- 习题
- - 习题1：AcWing 1223. 最大比例（中等，蓝桥杯）
  - - 分析
    - 题解：辗转相减法（更相减损术）
  - 习题2：Acwing 1301. C 循环（简单，扩展欧几里得）
  - - 分析
    - 题解：扩展欧几里得
二、DFS
- 习题
- - 习题1：AcWing 1225. 正则问题（中等，dfs与栈）
  - - 分析
    - 题解1：栈模拟
    - 题解2：dfs
  - 习题2：AcWing 1243. 糖果（状压+IDA*与dp状态压缩，蓝桥杯）
  - - 分析
    - 题解1：IDA*（dfs）
    - 题解2：状态压缩dp
参考文章

前言

前段时间为了在面试中能够应对一些算法题走上了刷题之路，大多数都是在力扣平台刷，目前是400+，再加上到了新学校之后，了解到学校也有组织蓝桥杯相关的程序竞赛，打算再次尝试一下，就想系统学习一下算法（再此之前是主后端工程为主，算法了解不多刷过一小段时间），前段时间也是第一次访问acwing这个平台，感觉上面课程也是比较系统，平台上题量也很多，就打算跟着acwing的课程来走一段路，大家一起共勉加油！

目前是打算参加Java组，所以所有的题解都是Java。

所有博客文件目录索引：博客目录索引(持续更新)

本章节贪心的习题一览：包含所有题目的Java题解链接

第八讲学习周期：2023.1.20-2023.1.27

例题：

AcWing 1246. 数论-例题等差数列（最大公约数，分析及Java题解）
AcWing 1295. 数论-例题 X的因子（算数基本定理、欧拉筛选，多重集合排列数，含详细分析及Java题解）
AcWing 1296. 数论-习题聪明的燕姿（欧拉筛+约数之和(dfs)+剪枝，分析及Java题解）
AcWing 1299. 数论—例题五指山（扩展欧几里得，分析及Java题解）

习题：

AcWing 1223. 数论-习题最大比例（辗转相减法，分析及Java题解）
AcWing 1301. 数论-习题 C 循环（扩展欧几里得，分析及Java题解）
AcWing 1225. DFS-习题正则问题（dfs、栈，分析及Java题解）
AcWing 1243. 数论-习题糖果（状压+IDA*、dp状态压缩，详细分析及Java题解）

一、数论

例题

例题1：AcWing 1246. 等差数列（最大公约数，第十届蓝桥杯省赛C++B第7题）

分析

数据量是10万，时间复杂度为O(n.logn)，O(n)。

首先等差数列如下所示：

x  x+d  x+2d  x+3d ... x+n*d

题目中说明只给出这一组等差数列的一小部分，让你去求得最短的等差数列个数，此时我们就需要通过这组给出的数列数字来去求得对应的d值，如何求到d值呢？

我们可以观察到等差数列中每一个数字都是由一个固定值x以及对应d的倍数组成的，那么我们此时就可以想到通过去使用最大公约数来去求得d。

举例：我们用x+3d - x = 3d，x + 3d - (x - d) = 2d，让2d 与3d来去进行最大公约数计算，即可求得d。

对于整个等差数列我们如何求得他们的数量呢？

数量 = (最大值 - 最小值) / d + 1

对于比较特殊的情况，例如：1 1 1，也就是d为0时，其数量应该就是n。

接着我们就可以去ac了！

题解：最大公约数

复杂度分析：时间复杂度O(n.logn)；空间复杂度O(n)

import java.io.*;
import java.util.*;

class Main {
    
    static final BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
    static final int N = 100010;
    static int n;
    static int[] a = new int[N];
    
    public static void main(String[] args) throws Exception{
        n = Integer.parseInt(cin.readLine());
        String[] ss = cin.readLine().split(" ");
        for (int i = 0; i < n; i++) {
            a[i] = Integer.parseInt(ss[i]);
        }
        //排序
        Arrays.sort(a, 0, n);
        //0可以作为起点来进行与之后的数字进行公约数计算
        int d = 0;
        for (int i = 0; i < n; i ++ ) {
            //a[i] - a[0]只留下对应的n * d，然后求取最大公约数
            d = gcd(d, a[i] - a[0]);
        }
        //若是最大公约数为0，直接返回整个个数
        //举例：0 0 0 0 0
        if (d == 0) {
            System.out.println(n);
        }else {
            //等差数列依次为：x  x+d  x+2d  x+3d，(最后一个-第一个) / d + 1 = 3 + 1 = 4
            System.out.println((a[n - 1] - a[0]) / d + 1);
        }
    }
    
    //计算最大公约数
    public static int gcd(int a, int b) {
        return b == 0 ? a : gcd(b, a % b);
    }
}

实际上我们可以去进行优化，因为排序的目的仅仅是为了找到最小值，最大值，我们只需要使用O(n)就可以找到了：

import java.io.*;
import java.util.*;

class Main {
    
    static final BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
    static final int N = 100010;
    static int n;
    static int[] a = new int[N];
    
    public static void main(String[] args) throws Exception{
        n = Integer.parseInt(cin.readLine());
        String[] ss = cin.readLine().split(" ");
        for (int i = 0; i < n; i++) {
            a[i] = Integer.parseInt(ss[i]);
        }
        //找到最小值，最大值
        int min = Integer.MAX_VALUE, max = Integer.MIN_VALUE;
        for (int i = 0; i < n; i ++) {
            min = Math.min(a[i], min);
            max = Math.max(a[i], max);
        }
        int d = 0;
        for (int i = 0; i < n; i ++ ) {
            //减去最小值
            d = gcd(d, a[i] - min);
        }
        if (d == 0) {
            System.out.println(n);
        }else {
            //最大值-最小值
            System.out.println((max - min) / d + 1);
        }
    }
    
    public static int gcd(int a, int b) {
        return b == 0 ? a : gcd(b, a % b);
    }
}

例题2：AcWing 1295. X的因子链（算数基本定理、欧拉筛选，多重集合排列数）

题目链接：1295. X的因子链

分析

本道题N大小为100万，时间复杂度应当控制在O(n.logn)、O(n)当中。

本道题去围绕我们两个求解的值来进行分析。

求解序列的最大长度：

这里的话我们需要去学习下算数基本定理，该定理说明：任何一个大于1的自然数 N,如果N不为质数，那么N可以唯一分解成有限个质数的乘积。所有的整数都可以唯一分解成若干个质因子乘积的形式。

该乘积公式为：N=P1^a1 P2^a2 P3^a3 * … Pn^an，这里P1<P2<P3…<Pn均为质数，其中指数ai是正整数。这样的分解称为 N 的标准分解式。最早证明是由欧几里得给出的。

根据该题题目说明要求：X 的大于 1 的因子组成的满足任意前一项都能整除后一项的严格递增序列。

举例严格递增情况：2    2*2    2*2*3   2*2*3*4

题目的说明完美的对准了算数基本定理：N=P1^a1 P2^a2 P3^a3 * … Pn^an，我们将一个数按照算数基本定理进行化解此时就可以得到序列的最大长度为a1 + a2 + a3 + a4 + … + an。

为什么呢？举个例子：

180 = 2² * 3² * 5

a1 = 2，a2 = 2，a3 = 1此时能够构成序列最大长度为5
//注意：题目中意思是去让你从对应因子组成中的数进行选择，例如2*2，你可以选择2以及4加入到这个序列当中去，不是说选了一个2，就只能再选一个2
//组成序列的如下，就是5
2   2*2   2*2*3   2*2*3*3   2*2*3*3*5

正是由于我们要根据算数基本定理这个公式，我们才需要去使用到欧拉筛法去求出来1 ~ n中所有的质数以及筛选出每一个数的最小质因子。（本题数据量为100万，欧拉筛法O(n)复杂度）

对于欧拉筛选法的思路及详细代码可见（包含朴素筛选、埃式筛选以及欧拉筛选）：数论之欧拉筛法（含朴素筛选、埃式筛选详细代码）

对于筛选出每一个数的最小质因子很关键，其能够去来推出对应的算数基本定理公式，例如180可以推出最小的质因数（质数）为2，接着180/4=45、45的最小质因数为3，45/9=5，5的最小质因子为5，最终构成：180 = 2² * 3² * 5。此时我们就可以拿到对应的a1，a2，a3…an，进而能够去求得序列的最大长度。

满足最大长度的序列的个数：实际上就是对最大长度的序列数进行全排列并进行去重

Y总的证明定理：先去做一个映射，不存数的本身，而是存数的增量，原序列是a1,a2,a3…an，映射的序列为a1, $a2\over a1$ , $a3\over a2$ … $an\over an-1$ ，这两个序列是对应的，给我们第一个序列就可以求第二个序列，在第二个序列中每一个数也同样都是质因子，因此序列个数就是所有质因子的全排列数（需要去掉重复数字情况）。

对于最大长度的序列我们还能够进行多种方案吗？下面来使用实际例子去进行举例对应上面的证明定理：180 = 2² * 3² * 5

2   2*2   2*2*3   2*2*3*3   2*2*3*3*5

//实际上我们还可以从3开始，同样能够构成最大长度序列
3   3*2   3*2*2   3*2*2*3   3*2*2*3*5

那么实际上我们就是对最大长度序列的数来进行求去安排列（去除掉相同元素的全排列）

多重集合公式学习：浅谈多重集排列组合
多重集排列数：对这N个元素全排列，除掉相同元素的全排列的积即可。

对应多重集排列数如下所示：

N个元素全排列：N!

去除相同元素如下举例：

3 3 3，相互可交换的次数为2*3，实际上就是ai!，ai指的是对应3的个数

最终去除掉相同元素的全排列为： $an)!\over a1!a2!...an!$

题解：数论-算数基本定理、欧拉筛选，多重集合排列数

复杂度分析：时间复杂度O(n)；空间复杂度O(n)

import java.util.*;
import java.io.*;

class Main {
    
    static final BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
    //2的20次方为1,048,576
    static final int N = 1100010;
    //存储合数
    static int[] coms = new int[N];
    //存储质数
    static int[] primes = new int[N];
    //存储质数的数量
    static int primeCount = 0;
    //存储所有数的最小质因子
    static int[] minPrimes = new int[N];
    static int x;
    
    //欧拉筛选
    public static void getPrimes(int n) {
        //遍历所有的数字
        for (int i = 2; i <= n; i++) {
            if (coms[i] == 0) {
                primes[primeCount++] = i;
                //存储质数的最小质因子，当前就是本身
                minPrimes[i] = i;
            }
            //遍历质数数组
            for (int j = 0; primes[j] * i <= n && j < primeCount; j++ ) {
                int t = primes[j] * i;//合数值
                //建立合数
                coms[t] = 1;
                //构建合数的最小质因子
                minPrimes[t] = primes[j];
                //若是当前i能够整除primes数组中的质数，此时直接提前结束
                if (i % primes[j] == 0) break;
            }
        }
    }
    
    public static void main(String[] args) throws Exception{
        //提前进行欧拉筛选
        getPrimes(N - 1);
        
        //来进行多轮操作
        while (true) {
            //读取两个数组
            String line = cin.readLine();
            if (line == null || line.length() == 0) break;
            //获取到数字
            int n = Integer.parseInt(line);
            //构建n = ...，基本的算数定理公式
            //使用fact、sum来分别记录N的质因子以及质因子的个数
            int[] fact = new int[100], sum = new int[100]; 
            //记录当前n的质因子的个数，对应fact的下标
            int k = 0;
            //记录质因子总数（题解1：序列的最大长度）
            int total = 0;
            //尝试去分解n的质因数
            while (n > 1) {
                //获取到当前n的最小质因子
                int minPrime = minPrimes[n];
                //设置第k个质因子为当前n的最小质因子
                fact[k] = minPrime;
                //对应第k个质因子数量从0开始计算
                sum[k] = 0;
                //为false情况：一旦不能够整除，此时就该要去找后一个不同的质因子
                while (n % minPrime == 0) {
                    //当前质因子数量+1
                    sum[k]++;
                    //质因子总数+1
                    total++;
                    n /= minPrime;
                }
                k++;
            }
            
            //开始计算（题解2：满足最大长度的序列的个数）
            long res = 1;
            //首先计算质因子总数的全排列方案数
            for (int i = 1; i <= total; i++) {
                res *= i;
            }
            //接着去除重复的情况
            //遍历所有的质因子
            for (int i = 0; i < k; i ++) {
                //每个质因子的阶乘（使用res继续除以）
                for (int j = 1; j <= sum[i]; j++) {
                    res /= j;
                }
            }
            
            //输出
            System.out.printf("%d %s\n", total, String.valueOf(res));
        }
        
    }
}

例题3：AcWing 1296. 聪明的燕姿

本质：暴搜+剪枝

学习文章：AcWing 1296. 聪明的燕姿—详细题解、AcWing 1296. 聪明的燕姿（蓝桥杯C++ AB组辅导课）—视频

分析

首先来理解题意：就是给你一个数的约数之和，让你求出多个符合这个条件的数(可能有多个)。

举例：约数和为42，数字20、26、41的约束之和都是42。
数字20的约数有：1 2 4 5 10 20，其和加起来为42。

本题暴力枚举的思路就是：对一个数S枚举从1到S-1的所有数的约数，再判断他们的约数和是否等于S。但是由于S最大为20亿，绝对会超时。

此时就可以使用约数之和的公式：S = (1+p1+p1²+…+p1^a1)(1+p2+p2²+…+p2^a2)…(1+pn+pn²+…+pn^an)

对应知识点及举例证明可见博客：约数个数及约数之和知识点(含公式)

若是有一个约数s满足上面公式，此时3x5x9x17x33x65x129 = 635037975，比较接近O(n)的复杂度，也就是该题的S最大值20亿。

对于这一个过程则是使用dfs来进行搜索，使用两层for循环来进行列举：

for(p : 2,3,5,7,...)
    for(a : 1,2,3,...)
        if(S mod (1+p1+p1^2+...+p1^a1) == 0)
            dfs(下一层)
//dfs(质数下标开始位置，上一层的实际答案结果，s剩余待整除的值)

下面给出约数之和为42的三个结果值20、26、41，可以看下使用约数之和公式来进行得到的结果值：

①20：1 2 4 5 10 20

20 = 2² * 5 = (2⁰+ 2¹ + 2²)*(5⁰+5¹)=42

②26：1 2 13 26

26 = 2 * 13 = (2⁰ + 2¹) * (13⁰ + 13¹) = 42

③41：1 41

41 = 41 = (41⁰ + 41¹) = 42

如何来使用剪枝去减少一些运算量呢？

我们可以发现实际的公式实际上是由() * ()的，所以我们实际的边界范围可以为sqrt(s)，对于这种情况，我们则需要去进行考虑特殊情况也就是S = (1 + pi)。
举个例子：若是约数之和为42，由于边界为sqrt(s)，此时那么遍历到的最大质数为7，而有一个结果数字为41，对于这种情况无法到达边界时，我们只需要考虑S = (1 + pi)中这个pi是否是一个质数即可，

另外本题需要去筛选质数，就需要使用到欧拉筛选实现O(n)复杂度，对于朴素筛选、埃拉筛选以及欧拉筛选思路及代码可见博客：数论之欧拉筛法（含朴素筛选、埃式筛选详细代码）。

题解：欧拉筛+约数之和(dfs)+剪枝

不进行sqrt()的dfs代码：需要开20亿个数组空间，无法ac该题

public static void dfs(int last, int pro, int s) {
    if (s == 1) {
        res[len++] = pro;
        return;
    }
    //你可以看到这里primes[i] <= s对于这种情况也依旧是可以实现的，但是对于本题S为20亿则会直接超时
    //优化点：对于primes[i] <= s / primes[i]则可直接对(s - 1)来判断进行优化。
    for (int i = last + 1; primes[i] <= s; i++) {
        int p = primes[i];
        for (int j = 1 + p; j <= s; p *= primes[i], j += p) {
            if (s % j == 0) {
                dfs (i, pro * p, s / j);
            }
        }
    }
}

添加剪枝优化：遍历sqrt(s)，添加s-1情况的判断条件

public static void dfs(int last, int pro, int s) {
    if (s == 1) {
        res[len++] = pro;
        return;
    }
    //剪枝（优化）：提前判断当前(s-1)是否是一个质数，若是(s-1)>上一个质数 && (s-1)是一个质数（主要也是解决数据量过大的问题）
    //对应下方for循环遍历的终点是：primes[i] <= s / primes[i]
    //举例：对于值为41，其约数为1、41，走下面的for循环(若是原本primes[i] <= s / primes[i])时，实际上只会遍历到最大质数为7就无法往后了，所以这边来进行提前剪枝操作
    int pre = last >= 0 ? primes[last] : 1;
    if (s - 1 > pre && isPrime(s - 1)) {
        res[len++] = pro * (s - 1);
    }
    for (int i = last + 1; primes[i] <= s / primes[i]; i++) {
        int p = primes[i];
        for (int j = 1 + p; j <= s; p *= primes[i], j += p) {
            if (s % j == 0) {
                dfs (i, pro * p, s / j);
            }
        }
    }
}

注意：使用java的话若是直接使用System.out.print会超时，建议使用BufferedReader和PrintWriter

完整代码：

import java.util.*;
import java.io.*;

class Main {
    
    static final BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
    static final PrintWriter out = new PrintWriter(new BufferedOutputStream(System.out));
    static final int N = 500000;//特判S = 1+p，最大S = p*p
    
    //欧拉筛所需要数组
    //flag表示合数数组，true为合数
    static boolean[] flag = new boolean[N];
    //存储质数
    static int[] primes = new int[N];
    static int cnt = 0;
    
    //存储每一组数据的答案
    static int[] res = new int[N];
    static int len = 0;
    
    //欧拉筛
    public static void getPrimes(int n) {
        //遍历所有情况
        for (int i = 2; i <= n; i++) {
            if (!flag[i]) primes[cnt++] = i;
            //枚举所有primes数组中的情况来提前构造合数
            for (int j = 0; j < cnt && primes[j] * i <= n; j ++) {
                int pre = primes[j] * i;
                flag[pre] = true;
                if (i % primes[j] == 0) break;
            }
        }
    }
    
    //dfs进行暴搜
    //last：表示上一个用的质数的下标(primes数组的下标)是什么
    //pro：当前计算res答案是多少
    //s: 表示每次处理一个()后还有剩余的值
    public static void dfs(int last, int pro, int s) {
        //表示当前已经把s凑出来了，记录答案
        if (s == 1) {
            res[len++] = pro;
            return;
        }
        //剪枝：提前判断当前(s-1)是否是一个质数，若是(s-1)>上一个质数 && (s-1)是一个质数
        //直接来进行计算res结果值
        int pre = last >= 0 ? primes[last] : 1;
        if (s - 1 > pre && isPrime(s - 1)) {
            res[len++] = pro * (s - 1);
        }
        //枚举所有以i作为下标的质数，实际就是N公式中的pi
        for (int i = last + 1; primes[i] <= s / primes[i]; i++) {
            int p = primes[i];
            //j指的是枚举()中的各种情况，例如i = 2，此时枚举情况为(1 + 2)、(1 + 2 + 2*2)、(1 + 2*2 + 2*2*2)
            for (int j = 1 + p; j <= s; p *= primes[i], j += p) {
                //当前能够整除情况则进入下一个层 
                if (s % j == 0) {
                    //下一层从primes下标为[i + 1]的开始(因为for循环是从last+1开始的)，当前括号*之前的值 = pro * p，若是j = (1 + 2 + 2*2)，此时
                    //p就是2*2=4，这个p实际上就是N公式里的一个2平方
                    //目标约数和为s，到了下一层其剩余和即为s / j
                    dfs (i, pro * p, s / j);
                }
            }
        }
    }
    
    //判断是否是质数（由于之前primes数组仅仅开了sqrt(20亿)也就只有50万，所以这里需要进行遍历一遍质数数组来进行判断校验）
    public static boolean isPrime(int x) {
        //若是x在50万范围，直接从flag数组中判断返回即可
        if (x < N) return !flag[x];
        //若是>=50万，那么就进行遍历质数数组看是否有能够整除的，如果有那么直接返回
        for (int i = 0; primes[i] <= x / primes[i]; i++) {
            if (x % primes[i] == 0) return false;
        }
        return true;
    }
    
    public static void main(String[] args) throws Exception{
        //欧拉筛
        getPrimes(N - 1);
        String line = cin.readLine();
        //读取数据
        while (line != null && line.length() > 0) {
            //目标约数之和为s
            int s = Integer.parseInt(line);
            dfs(-1, 1, s);
            out.println(len);
            if (len != 0) {
                //对结果进行排序
                Arrays.sort(res, 0, len);
                //输出
                for (int i = 0; i < len; i++) {
                    out.print(res[i] + " ");
                }
                out.println();
                len = 0;//重置结果数组的长度为0
            }
            out.flush();
            line = cin.readLine();
        }
    }
}

例题4：AcWing 1299. 五指山（扩展欧几里得）

分析

总长度为n，每次翻跟斗距离d，初始位置为x，目标位置为y，若是不能够到达目标点输出Impossible，若是能够达到则输出最少翻跟斗的次数。

本道题对应2的公式为：x + b.d = y (mod n)，含义就是从x点出发，加上b次翻跟斗的距离最终得到的位置为目标点mod整个圈距离。

再转换下：x + b.d = y (mod n) = y + a.n，意思就是y点，加上a圈环形长度。

x + b.d = y + a.n转换下式子，其中x, d, y, n是已知的，转为：-a.n + b.d = y - x

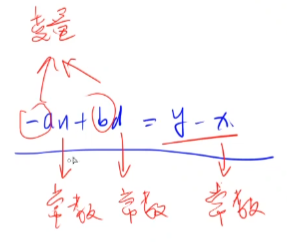
注意：此时这个式子就与扩展欧几里得的式子相对应，gcd(a, b) = d，对应的等式a.x + b.y = d成立，可以利用扩展欧几里得来进行反推出本道题式子中的a与b。

此时本题的思路就是：通过使用扩展欧几里得算法来求出gcd(n, d) = gcd，然后判断y-x是否能够整除得到的最大公约数，若是不能整除输出Impossible，能够整除则来进行计算最少的翻跟斗次数。

为什么y-x是否能够整除得到的gcd就能够判定是否无解？

因为-a.n + b.d得到的是一个最大公约数，若是得到的最大公约数不能够整除y - x，那么就肯定无解，则就输出impossible。

如何去计算最少的翻跟斗次数呢？

我们来去进行扩展欧几里得计算时实际上计算得到的式子为：-a.n + b.d = gcd(n, d)，而对于题目应该是-a.n + b.d = y - x，为了让右边式子也有y-x，此时我们需要两边都乘上(y - x) / gcd(n, d)，此时b才是我们最终-a.n + b.d = y - x的b结果值！

而此时b的值仅仅只是-a.n + b.d = y - x中的一组ab解，而去利用扩展欧几里得公式即可通过一组解来得到所有的ab解，那么我们只要得到最小的一个b解即可！

在扩展欧几里得公式中，若是公式为ax+by=gcd(a, b)，对应的b = b0 - k.b’，此时我们想要得到b0的最小值即可通过使用b0 mod b’即可得到最小值。【其中b’ = b /d，详细推导过程可见：欧几里得与扩展欧几里得算法(含推导过程及代码)】

对应当前题目-a.n + b.d = y - x我们要得到b的最小值，首先得到如下两个式子：

b = b0 - kn’
n’ = n / (y - x)

此时当前b的所有解为b = b0 - k.(n / d)，其中n与d是常量，对于我们要求出b的最小值，只需要使用b0 % ( n / (y - x))即可，这个b0实际上是可以求到的，但是我们不能够确定k，所以我们可以直接使用得到的结果值b来进行mod，也就是最终最小值为b = b mod (n /(y - x))。

而由于为了避免b mod (n /(y - x))出现负数情况，我们令n = n / (y - x)，接着(b mod n + n) % n即可将负数转化为正数！

题解：扩展欧几里得

复杂度分析：时间复杂度O(logn)；空间复杂度O(1)

import java.io.*;
import java.util.*;

class Main {
    
    static final Scanner cin = new Scanner(System.in);
    
    static int t;
    static long n, d, x, y;
    
    //扩展欧几里得
    public static long exGcd(long a, long b, long[] arr) {
        if (b == 0) {
            arr[0] = 1;
            arr[1] = 0;
            return a;
        }
        //递归求得最大公约数
        long gcd = exGcd(b, a % b, arr);
        //反向推导求得一组x，y解： x = y'，y = x' - a/b*y'
        long temp = arr[0];
        arr[0] = arr[1];
        arr[1] = temp - a / b * arr[1];
        return gcd;
    }
    
    public static void main(String[] args) {
        int t = cin.nextInt();
        while (t != 0) {
            //读取数据
            n = cin.nextLong();
            d = cin.nextLong();
            x = cin.nextLong();
            y = cin.nextLong();
            long[] arr = new long[2];
            //获取到最大公约数和一组xy解
            long gcd = exGcd(n, d, arr);
            //得到一组x与y解（这里用a与b表示）
            long a = arr[0];
            long b = arr[1];
            //若是y - x能够整除gcd(n, d)那么此时就说明有解
            if ((y - x) % gcd != 0) {
                System.out.println("Impossible");
            }else {
                //ax + by = gcd(a, b)  转换为  ax + by = y - x，所以两边需要乘上(y - x) / gcd(a, b)
                b *= (y - x) / gcd;
                //接着需要进行计算最小值：b = b0 - kn’、n’  = n / (y - x)
                //由于上面式子转换仅仅只是b变量进行了转换，所以n依旧使用原先的gcd进行转换
                n /= gcd;
                //避免b % n为负数情况
                System.out.println((b % n + n) % n);
            }
            
            t--;
        }
    }
}

习题

习题1：AcWing 1223. 最大比例（中等，蓝桥杯）

分析

题目链接：AcWing 1223. 最大比例

本道题是给你一个等比数列，比值是恒定的，但是题目只会给出等比数列中的部分个，让你求得等比数列中最大的等比值是多少。

数据量不大，等比数列中的数给出仅有10个，仅仅只是其中最大值比较大需要使用long类型。

假设完整的原定等差数列为：a, a * $\frac{p}{q}$ ， a * ( $\frac{p}{q}$ )²， a * ( $\frac{p}{q}$ )³， a * ( $\frac{p}{q}$ )⁴, … ， a * ( $\frac{p}{q}$ )^n-1。

我们去抽取其中的几个为：b1, b2, b3, b4，那么其中每个数的组成即为 ( $\frac{p}{q}$ )^k，对于每一组b[i]针对b[i - 1]的比值我们可以求到的，即： $\frac{p^k}{q^k}$ 中的p^k以及q^k，对于这两个上下值我们可以通过求得最大公约数来进行获取。

此时又回到题目说让我们求得( $\frac{p}{q}$ )^k的最大值，实际上即为让我们求指数的最大公约数，而对于指数的最大公约数我们则需要使用辗转相减法，知识点可见：辗转相除以及辗转相减法

通过辗转相减法gcd(x,y) = gcd(y,x%y) = gcd(y,x−y)来进行推导：f(p^x,p^y) = p^gcd(x,y) = p^gcd(y,x−y) = f(p^y,p(^x−y)) = f(p^y, $\frac{px}{py}$ )，即可以求

求p^x和p^y幂的最大公约数次幂p^gcd(x,y)。

为什么指数不能够使用辗转相除法呢？见如下例子，本题中的辗转相减法是减得指数

使用辗转相除法：gcd(5²，5³) = 5²
使用辗转相减法：gcd_sub(5²，5³) = 5¹

题解：辗转相减法（更相减损术）

复杂度分析：时间复杂度O(n.logn)，排序复杂度；空间复杂度O(n)

import java.util.*;
import java.io.*;

class Main {
    
    static final BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
    static final int N = 110;
    static int n;
    static long[] x = new long[N], p = new long[N], q = new long[N];
    
    
    //最大公约数(辗转相除)
    public static long gcd(long a, long b) {
        return b == 0 ? a : gcd(b, a % b);
    }
    
    //辗转相减，求得指数的最小公约数
    public static long gcd_sub(long a, long b) {
        if (a < b) {
            long temp = b;
            b = a;
            a = temp;
        }
        if (b == 1) return a;
        return gcd_sub(b, a / b);
    }
    
    public static void main(String[] args) throws Exception{
        n = Integer.parseInt(cin.readLine());
        String[] ss = cin.readLine().split(" ");
        for (int i = 0; i < n; i ++ ) {
            x[i] = Long.parseLong(ss[i]);
            //System.out.println(x[i]);
        }
        //对所有数字进行排序
        Arrays.sort(x, 0, n);
        
        
        //记录p与q数组成对的数量
        int cnt = 0;
        
        //查询所有数字乘数p/q的p与q的值
        for (int i = 1; i < n; i ++ ) {
            if (x[i] != x[i - 1]) {
                //获取到两个数的最大公约数
                long gcd = gcd(x[i], x[0]);
                //利用最大公约数来计算得到分数中的p与q
                p[cnt] = x[i] / gcd;
                q[cnt++] = x[0] / gcd;
            }
        }
        
        //开始计算所有(p/q)^n最大公约数
        long P = p[0];
        long Q = q[0];
        for (int i = 1; i < cnt; i ++ ) {
            P = gcd_sub(P, p[i]);
            Q = gcd_sub(Q, q[i]);
        }
        System.out.println(P + "/" + Q);
    }
}

习题2：Acwing 1301. C 循环（简单，扩展欧几里得）

题目链接：Acwing 1301. C 循环

分析

k位系统指的是所有变量只能存储k位。那么每次+c的值实际上就是mod 2^k的值。

此时我们即可列出等式：(A + x.C) mod 2^k = B，其中A，C，B是定值，由mod 2^k实际上可以替换为y.2^k。

此时(A + x.C) mod 2^k = B 转换为 A + x.C - y.2^k = B 转换为 x.C - y.2^k = B - A

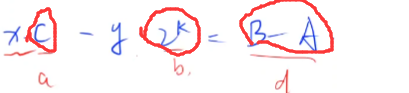红圈的则都是常量。

此时我们就可以想到扩展欧几里得：xa + yb = d，可以反推得到x与y的一组解，而又由一组解得到所有解。

对于扩展欧几里得的证明与结论可看：欧几里得与扩展欧几里得算法(含推导过程及代码)

对应得到的公式如下所示：

实际上最终我们得到该题的公式如下：

x' = x / (B - A)
y' = y / (B - A)

x = x0 + ky'
y = y0 + kx'

对于判断是否能够循环所有次数我们只需要去判断B - A是否能够mod gcd(a, b)即可最终我们要求得是循环的次数数量则就是x = x0 % y’。

题解：扩展欧几里得

复杂度分析：时间复杂度O(logn)；空间复杂度O(1)

import java.util.*;
import java.io.*;

class Main {
    
    static final Scanner cin = new Scanner(System.in);
    static long A, B, C, K;
    
    //扩展欧几里得
    public static long exGcd(long a, long b, long[] arr) {
        if (b == 0) {
            arr[0] = 1;
            arr[1] = 0;
            return a;
        }
        long d = exGcd(b, a % b, arr);
        //通过公式去化解转为 x = y'，y = x‘ - a/b*y'
        long temp = arr[0];
        arr[0] = arr[1];
        arr[1] = temp - a / b * arr[1];
        return d;
    }
    
    public static void main(String[] args) throws Exception{
        while(!isStop()) {
            //若是A==B，则输出0
            if (A == B) {
                System.out.println(0);
                continue;
            }
            // x.C - y.2^k = B - A
            //计算C与2^k的最大公约数
            long[] arr = new long[2];
            //提前定义好 x.C + y.2^k = gcd(C, 2^k)  =>  用a替代为C，b替代为2^k
            long a = C;
            long b = 1L << K;//注意，这个b变量必须使用1L，表示long类型，否则有误
            long gcd = exGcd(a, b, arr);
            if ((B - A) % gcd != 0) {
                System.out.println("FOREVER");
            }else {
                long x = arr[0];
                long y = arr[1];
                //将 x.a + y.b = gcd(a, b) 转为  x.a - y.b = B - A
                //此时只需要将这个x去进行一个转换
                x *= (B - A) / gcd;
                
                //若是想要取得一个最小运行次数x
                //y' = y / gcd
                b = b / gcd;
                
                //取得最小整数  x = x0 % b
                System.out.println((x % b + b) % b);
            }
        }
    }
    
    public static boolean isStop() throws Exception{
        A = cin.nextLong();
        B = cin.nextLong();
        C = cin.nextLong();
        K = cin.nextLong();
        return A == 0 && B == 0 && C == 0 && K == 0;
    }
}

二、DFS

习题

习题1：AcWing 1225. 正则问题（中等，dfs与栈）

分析

首先去理解题意，总共有|、()、x四个符号，下面来进行举例：

xx|xxx    =>  xxx     //|选择左右两边最多的一组
(xx|xxx)x   => xxxx   //()与左右两边进行相连接

题目给定范围是100，且保证合法。

栈模拟思路：

遇到(、x、|符号直接入栈
遇到)开始进行匹配规则：
	循环出栈直到出现(，过程中可能会有|来进行计数判断选择最大的个数，最终来进行出栈(

dfs思路：把整个字符串想象成树，对字符串从左到右来进行dfs。

①若是碰到(则向下递归一层直到匹配到)结束。
②若是碰到|则将|xxx右边的进行dfs()递归将其得到的长度与当前的长度取一个最大值。
③若是碰到)则直接break结束。
④若是碰到x此时进行res+1。

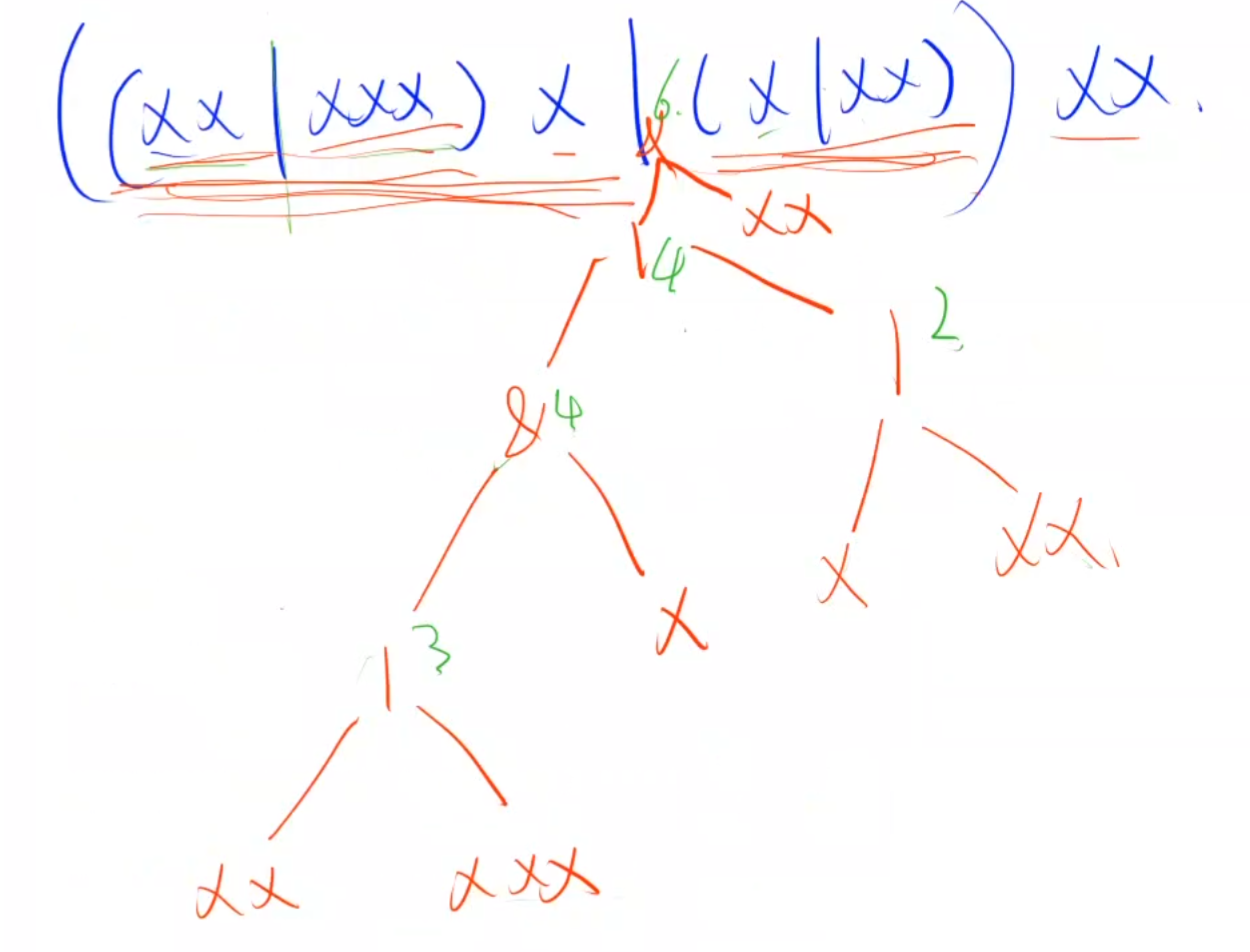
题解1：栈模拟

复杂度分析：时间复杂度O(n)；空间复杂度O(n)

import java.util.Scanner;
import java.util.Stack;

class Main {

    static final Scanner cin = new Scanner(System.in);
    static Stack<Character> s = new Stack<>();
    
    //假设碰到)时来进行的计数操作
    public static void count() {
        //碰到)
        int cnt = 0;
        int c = 0;
        while (!s.isEmpty() && s.peek() == 'x') {
            c++;
            s.pop();
            cnt = Math.max(cnt, c);
            //如果说碰到了|，重新计数
            if (!s.isEmpty() && s.peek() == '|') {
                c = 0;
                s.pop();
            }
        }
        if (!s.isEmpty() && s.peek() == '(') {
            //此时碰到(
            s.pop(); 
        }
        //入栈cnt个x
        for (int i = 1; i <= cnt; i++) {
            s.push('x');
        }
    }

    public static void main(String[] args) {
        String line = cin.next();
        for (char ch: line.toCharArray()) {
            if (ch == '(' || ch == '|' || ch == 'x') {
                s.push(ch);
            }else {
                count();
            }
        }
        //结束之后再计算下，可能会出现情况：xx|xxxxx
        count();
        System.out.println(s.size());

    }
}

题解2：dfs

复杂度分析：时间复杂度O(n)；空间复杂度O(n)

import java.util.*;
import java.io.*;

class Main {
    
    static final Scanner cin = new Scanner(System.in);
    static char[] arr;
    static int k;
    
    //计数
    public static int dfs() {
        int res = 0;
        while (k < arr.length) {
            //匹配(.....)
            if (arr[k] == '(') {
                k++;
                res += dfs();
                k++;
            }else if (arr[k] == ')') { //(的结束递归
                break;
            }else if (arr[k] == '|') {  //比较左右最大数量 ...|...
                k++;
                res = Math.max(res, dfs());
            }else {
                //若是碰到x
                k++;
                res++;
            }
        }
        return res;
    }
    
    public static void main(String[] args) {
        arr = cin.next().toCharArray();
        int res = dfs();
        System.out.println(res);
        cin.close();
    }
    
}

习题2：AcWing 1243. 糖果（状压+IDA*与dp状态压缩，蓝桥杯）

题目链接：AcWing 1243. 糖果

分析

思路1：状态压缩+IDA*（dfs）

重复覆盖问题可以考虑使用IDA*。

重复覆盖问题：即给定一个矩阵，选定最少的行使所有的列都会被覆盖。

对于IDA*需要来进行考虑三个部分：

迭代加深：进行逐层判断，是否能够完全覆盖。
选择最少的列：尽可能选择情况少的来进行搜索。
可行性剪枝：通过使用一个估价函数h(state)表示对于状态state至少需要多少行。若是符合当前的搜索的行数则继续向下，若是不符合提前剪枝结束。

整个完整思路可见代码注释，很详细。

这里我再贴一下状态压缩进行二进制操作的一些说明：

思路2：状态压缩dp

状态表示：f[i][j]表示前i包糖果，状态为j的最小糖果包数选择数量。

初始化：f[i][0]=0，其他默认为最大值。

状态计算：f[i][j] = min(f[i][j], f[i][j & ~c[i]] + 1)

j & ~c[i]表示的是目标状态二进制值与c[i] 进行|合并为当前状态二进制值j。

题解1：IDA*（dfs）

复杂度分析：时间复杂度O(b ^ d)，其中b是分支因子，d是第一个解决方案的深度。空间复杂度O(d)

import java.util.*;
import java.io.*;

class Main {
    
    static final BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
    static final int N = 110, K = 22;
    //n表示行数，m表示糖果种类数量，k表示每袋有几个糖果
    static int n, m, k;
    //candy表示每袋糖果的二进制表示
    //log2表示根据二进制位去映射对应的糖果品类，下标是二进制位，值就是糖果品类编号
    //若是key：0001也就是1，value就是糖果品类编号0
    //若是key: 0010也就是2，value就是糖果品类编号1
    //糖果品类有M种，默认在初始化时进行编号0 - M-1
    static int[] candy = new int[N], log2 = new int[1 << K];
    //存储key为糖果类型编号，value为糖果包装有该糖果编号的二进制值
    static Map<Integer, List<Integer>> map = new HashMap<>();
    
    
    public static void main(String[] args) throws Exception{
        String[] ss = cin.readLine().split(" ");
        n = Integer.parseInt(ss[0]);
        m = Integer.parseInt(ss[1]);
        k = Integer.parseInt(ss[2]);
        //初始化糖果品类编号对应二进制位的映射
        //log2[1] = 0，log2[2] = 1，log2[4] = 2 ... 
        for (int i = 0; i < m; i ++ ) {
            log2[1 << i] = i;
        }
        //读取每袋糖果
        for (int i = 0; i < n; i ++ ) {
            ss = cin.readLine().split(" ");
            //对每袋糖果中的多个品类来进行状态压缩到一个二进制curCandy
            int curCandy = 0;
            for (int j = 0; j < k; j ++ ) {
                int candyType = Integer.parseInt(ss[j]);//读取到糖果编号
                //curCandy更新当前的糖果袋子具有的糖果种类，例如二进制形式curCandy = 00000，candyType = 1，而之前在log2中说明糖果种类为[0,M-1]
                //所以(1 << (candyType - 1))即为00001，此时00000 | 00001 = 00001
                //同上其他情况，curCandy = 00001，candyType = 3，此时此时00001 | 00100 = 00101
                curCandy = curCandy | (1 << (candyType - 1));
            }
            
            candy[i] = curCandy;//将每袋糖果具有的糖果类别进行状态压缩后添加到candy数组中
            
            //记录指定糖果类型编号有哪些袋糖果
            for (int j = 0; j < m; j ++ ) {
                //判断当前糖果包中是否有对应编号为j的糖果
                if (((curCandy >> j) & 1) == 1) {
                    if (!map.containsKey(j)) {
                        map.put(j, new ArrayList<>());
                    }
                    List<Integer> packages = map.get(j);
                    packages.add(curCandy);
                }
            }
        }
        //若是在map中具有的糖果类型种类没有m个，那么直接结束
        if (map.size() < m) {
            System.out.println("-1");
        }else {
            //1、迭代加深
            //进行尝试递归寻找糖果包方案数量
            int count = 0;
            //数量上限为糖果的品类，若是超过上限还没有找到说明肯定没有该方案
            while (count <= m) {
                //判断当前选择count数量的糖果包是否能够集全
                if (dfs(count, 0)) {
                    break;
                }else {
                    count++;
                }
            }
            //此时得到方案数
            System.out.println(count);
        }
    }
    
    //尝试寻找方案数量
    //count：表示当前还能选择的糖果包数量
    //state：表示当前已选糖果类型的状态，若是M为5，达到11111即可表示已经选中
    public static boolean dfs(int count, int state) {
        //3、使用估价函数来判断当前状态是否能够继续往下进行
        //若是当前不能选糖果包了 或者 还可以选并且至少需要糖果包的数量>当前剩余的数量
        if (count == 0 || mustNeed(state) > count) {
            //若是m为5，则判断当前已经状态state是否为11111
            return state == (1 << m) - 1;
        }
        //2、选择尽可能少的列
        //寻找还没有凑齐的多个糖果类型(从右往左开始)中最少糖果包的那个糖果列
        int minCol = -1;
        for (int i = (1 << m) - 1 - state; i > 0; i -= lowbit(i)) {
            //获取到二进制位从右往左第一个1，也就是第一个还未选择的糖果类型
            int col = log2[lowbit(i)];
            if (minCol == -1 || map.get(minCol).size() > map.get(col).size()) {
                minCol = col;
            } 
        }
        //枚举最少数量的糖果类型列，进行递归处理
        for (int pack: map.get(minCol)) {
            //还能选择的糖果数量-1，当前已经选择糖果状态列补上当前糖果包有的糖果列
            //state为00101，pack为00010，此时state | pack即为00111
            if (dfs(count - 1, state | pack)) {
                return true;
            }
        }
        return false;
    }
    
    //当前状态最少需要的糖果包数
    //state：表示当前已选糖果类型的状态
    public static int mustNeed(int state) {
        int ans = 0;
        //(1 << m) - 1 - state：表示的是当前还未选的糖果类型二进制状态
        for (int i = (1 << m) - 1 - state; i > 0;) {
            //当前所需要的糖果类型行号
            int col = log2[lowbit(i)];
            //获取到对应糖果类型的所有糖果
            List<Integer> packages = map.get(col);
            //来将该行对应的所有糖果包都去进行消除当前i二进制状态中与糖果包共有的1
            for (int pack: packages) {
                //假设i二进制为：11111，pack为00101
                //那么i & ~pack = 11010，相当于消去该糖果包有的糖果类型
                //~pack实际上就是表示所有二进制为取反，原本pack=00100，~pack即可转为11011
                i = i & ~pack;
            }
            ans++;
        }
        return ans;
    }
    
    //从右往左得到第一个1的下标k（从0开始），返回的结果值为2^k
    //例如x的二进制位0010，此时下标k为1，返回值就是2^1 = 2
    public static int lowbit(int x) {
        return x & -x;
    }
    
}

题解2：状态压缩dp

复杂度分析：时间复杂度O(n.2^m)，又m最大为20，就是100*104万，大概一千万运算量。空间复杂度O(2^m)

import java.io.*;
import java.util.*;

class Main {
    
    static final BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
    static final int N = 110, K = 20, INF = 101;
    //c表示所有糖果包的状态压缩；
    static int[] c = new int[N];
    //f表示从前i个物品中选且状态是j的最小糖果包数量。
    static int[] f = new int[1 << K + 5];
    static int n, m, k;
    
    public static void main(String[] args) throws Exception{
        String[] ss = cin.readLine().split(" ");
        n = Integer.parseInt(ss[0]);
        m = Integer.parseInt(ss[1]);
        k = Integer.parseInt(ss[2]);
        //初始化每个糖果包的状态压缩
        for (int i = 1; i <= n; i ++ ) {
            ss = cin.readLine().split(" ");
            for (int j = 1; j <= k; j ++ ) {
                int candyType = Integer.parseInt(ss[j - 1]);
                c[i] |= 1 << (candyType - 1);
            }
        }
        //初始化状态数组
        for (int i = 1; i < 1 << m; i ++ ) f[i] = INF;
        //一种口味都没有情况最少是0包糖果
        f[0] = 0;
        //遍历所有的糖果包
        for (int i = 1; i <= n; i ++ ) {
            //遍历所有1 - 2^m-1状态（从大到小）
            for (int j = (1 << m) - 1; j >= 0; j -- ) {
                //j & ~c[i]表示当前二进制状态j去除掉c[i]状态的共有1
                f[j] = Math.min(f[j], f[j & ~c[i]] + 1);
            }
        }
        if (f[(1 << m) - 1] == INF) {
            System.out.println("-1");
        }else {
            System.out.println(f[(1 << m) - 1]);
        }
    }
}

参考文章

[1] 例题1等差数列：AcWing 1246. 等差数列-题解1、AcWing 1246. 等差数列-题解2 、AcWing 1246. 等差数列（蓝桥杯C++ AB组辅导课）-y总视频讲解

[2] 例题3 聪明的燕姿：AcWing 1296. 聪明的燕姿—详细题解、AcWing 1296. 聪明的燕姿（蓝桥杯C++ AB组辅导课）—视频、AcWing 1296. 聪明的燕姿(Java)

[3]. 例题4 五指山：AcWing 1299. 五指山—题解、AcWing 1299. 五指山(拓展欧几里德X1、Y1、X2、Y2的关系)、AcWing 1299. 数论-扩展欧几里得

[4]. 习题1 最大比例：AcWing 1223. 最大比例（Java版）

[5]. 正则问题：AcWing 1225. Java中缀表达式思路+递归两种解法、AcWing 1225. 正则问题（蓝桥杯C++ AB组辅导课）、AcWing 1225. 正则问题-栈做法

[6]. 糖果：algorithm - 人工智能：IDA *搜索的时间复杂性、AcWing 1243. 糖果(IDA* / 状压DP 详细注释) 、AcWing 1243. 糖果(Java版) 、AcWing 1243. 糖果–>dfs+剪枝+排序优化+去除优化+IDA*+状压、AcWing 1243. 糖果（蓝桥杯C++ AB组辅导课）