快乐的流畅：个人主页

个人专栏：《算法神殿》《数据结构世界》《进击的C++》

远方有一堆篝火，在为久候之人燃烧！

---

引言

数据结构世界——顺序表（Sequential List）

一、顺序表的概念

1.1 最基础的数据结构：数组

【思考】有了数组，为什么还要学习其他的数据结构？

假定数组有10个空间，已经使用了5个，向数组中插入数据步骤：求数组的长度，求数组的有效数据个数，向下标为数据有效个数的位置插入数据（注意：这里是否要判断数组是否满了，满了还能继续插入吗）…

---

假设数据量非常庞大，频繁的获取数组有效数据个数会影响程序执行效率。

结论：最基础的数据结构能够提供的操作已经不能完全满足复杂算法实现。

1.2 数组与顺序表的区别

顺序表的底层结构是数组，对数组的封装，实现了常用的增删改查等接口。

二、静态顺序表

//静态顺序表
#define N 10
typedef int SLDataType;

typedef struct SeqList
{
	SLDataType a[N];
	int size;
}SL;

​​​​

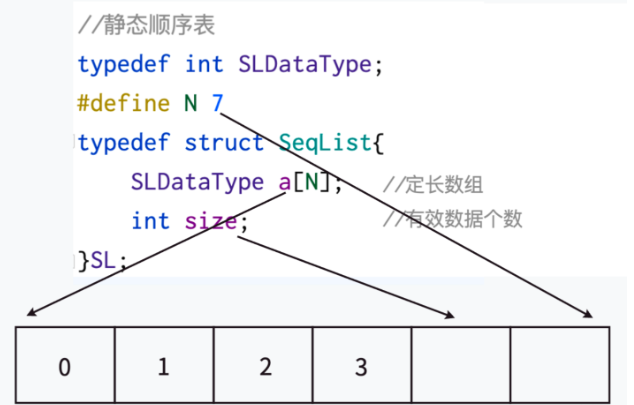
静态顺序表缺陷：空间给少了不够用，给多了造成空间浪费。

三、动态顺序表的模拟实现

3.1 定义

//动态顺序表
typedef int SLDataType;

typedef struct SeqList
{
	SLDataType* a;
	int size;//存储的有效数据的个数
	int capacity;//容量
}SL;

顺序表的各种功能，都是通过函数来实现的。

3.2 初始化

void SLInit(SL* psl)
{
	assert(psl);
	psl->a = (SLDataType*)malloc(sizeof(SLDataType) * 4);
	if (psl->a == NULL)
	{
		perror("malloc fail");
		return;
	}
	psl->size = 0;
	psl->capacity = 4;
}

• 函数参数传结构体指针，这样才能在函数内部对顺序表进行各种解引用操作
• 对于动态顺序表，初始化则用malloc函数动态开辟内存空间 ；存储个数为0，容量初始置为4

3.3 销毁

void SLDestroy(SL* psl)
{
	assert(psl);
	free(psl->a);
	psl->a = NULL;
	psl->size = 0;
	psl->capacity = 0;
}

• 对于用free函数将动态开辟的空间进行释放，并将指针置为NULL ；再将存储个数和容量置为0

3.4 扩容

数组满了怎么办？那么，我们就需要扩容，定义一个函数专门来检测容量，如果容量满了，则进行扩容。

static void CheckCapacity(SL* psl)
{
	assert(psl);
	if (psl->size == psl->capacity)
	{
		SLDataType* tmp = (SLDataType*)realloc(psl->a, sizeof(SLDataType) * psl->capacity * 2);
		if (tmp == NULL)
		{
			perror("realloc fail");
			return;
		}
		psl->a = tmp;
		psl->capacity *= 2;
	}
}

• 我们使用realloc函数动态开辟空间进行扩容，而扩容的大小则为原来容量的2倍 （这样比较合理，扩容多了浪费空间，扩容少了空间又不够）

3.5 尾插

void SLPushBack(SL* psl, SLDataType x)
{
	assert(psl);
	CheckCapacity(psl);
	psl->a[psl->size++] = x;
}

• 对于psl指针，如果有人误传了NULL，则会导致程序崩溃，所以最好在每个函数前断言assert，保证psl指针的有效性
• 先检测是否需要扩容
• 再根据当前已有的元素个数，对数组进行下标访问并赋值，size++

3.6 头插

void SLPushFront(SL* psl, SLDataType x)
{
	assert(psl);
	CheckCapacity(psl);
	int end = psl->size - 1;
	while (end >= 0)
	{
		psl->a[end + 1] = psl->a[end];
		end--;
	}
	psl->a[0] = x;
	psl->size++;
}

• 先检测是否需要扩容
• 再用循环将数组中每个元素向后挪动一格，最后在头部插入数据，size++

3.7 尾删

void SLPopBack(SL* psl)
{
	assert(psl);
	assert(psl->size > 0);
	psl->size--;
}

• 使用断言assert，保证size大于零，不会造成越界访问
• 直接让size- -，使得不再能够访问尾部数据

3.8 头删

void SLPopFront(SL* psl)
{
	assert(psl);
	assert(psl->size > 0);
	int start = 0;
	while (start < psl->size - 1)
	{
		psl->a[start] = psl->a[start + 1];
		start++;
	}
	psl->size--;
}

• 用循环将数组中每个元素向前挪动一格，覆盖头部数据，实现头部删除，size- -

3.9 指定插入

void SLInsert(SL* psl, int pos, SLDataType x)
{
	assert(psl);
	assert(pos >= 0 && pos <= psl->size);
	CheckCapacity(psl);
	int end = psl->size - 1;
	while (end >= pos)
	{
		psl->a[end + 1] = psl->a[end];
		end--;
	}
	psl->a[pos] = x;
	psl->size++;
}

• 断言assert保证pos不会越界
• 输入指定位置的下标，用循环将pos往后的所有数据向后挪动一格 ，再于指定位置插入数据，size++

---

我们可以运用这个应用更广的指定插入，来实现头插和尾插 ，以此增强函数的复用性。

尾插

void SLPushBack(SL* psl, SLDataType x)
{
	assert(psl);
	SLInsert(psl, psl->size, x);
}

头插

void SLPushFront(SL* psl, SLDataType x)
{
	assert(psl);
	SLInsert(psl, 0, x);
}

3.10 指定删除

void SLErase(SL* psl, int pos)
{
	assert(psl);
	assert(pos >= 0 && pos < psl->size);
	int start = pos + 1;
	while (start < psl->size)
	{
		psl->a[start - 1] = psl->a[start];
		start++;
	}
	psl->size--;
}

• 断言assert保证pos不会越界（此处与指定插入比少了一个等号，仔细思考一下为什么？）
• 输入指定位置的下标，用循环将pos往后的所有数据向前挪动一格 ，以此覆盖pos位置的数据，达到指定删除的目的

---

我们可以运用这个应用更广的指定删除，来实现头删和尾删 ，以此增强函数的复用性。

尾删

void SLPopBack(SL* psl)
{
	assert(psl);
	SLErase(psl, psl->size - 1);
}

头删

void SLPopFront(SL* psl)
{
	assert(psl);
	SLErase(psl, 0);
}

3.11 查找

int SLFind(SL* psl, SLDataType x)
{
	assert(psl);
	int i = 0;
	for (i = 0; i < psl->size; i++)
	{
		if (psl->a[i] == x)
		{
			return i;
		}
	}
	return -1;
}

• for循环遍历数组，找到返回下标，找不到返回-1

3.12 修改

void SLModify(SL* psl, int pos, SLDataType x)
{
	assert(psl);
	assert(pos >= 0 && pos < psl->size);
	psl->a[pos] = x;
}

• 直接通过下标访问数组进行修改

3.13 打印

void SLPrint(SL* psl)
{
	assert(psl);
	int i = 0;
	for (i = 0; i < psl->size; i++)
	{
		printf("%d ", psl->a[i]);
	}
}

真诚点赞，手有余香